Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум

Подождите немного. Документ загружается.

Заметим, что ценность видов ресурсов нельзя отождествлять с дей-

ствительными ценами, по которым осуществляется его закупка. В дан-

ном случае речь идет о некоторой мере, имеющей экономическую при-

роду, которая характеризует ценность ресурса только относительно по-

лученного оптимального решения.

Анализ эффективности отдельных вариантов плана выполняется

на основе соотношений из 2-й теоремы двойственности:

если

Xj>0,

то^а,j

-Y,

=Cj^

j-\,...,n;

i=\

если

',y

Y,>C

TOX,=0,

j=\,...,n.

(=1

Если изделие вошло в оптимальный план

(X,

> 0), то в двойствен-

ных оценках оно не убыточно, т.е. стоимость ресурсов, затраченных на

производство единицы изделия, равна его цене. Такие изделия эффек-

тивны, выгодны с точки зрения принятого критерия оптимальности. В

нашей задаче это ковры второго и третьего видов.

Если стоимость ресурсов, затраченных на производство одного из-

делия, больше его цены, то это изделие не войдет в оптимальный план

из-за его убыточности. В нашей задаче в план выпуска не вошли ковры

первого и четвертого видов, потому что затраты по ним превышают цену

на 7 (10 - 3) тыс. руб. и

9.666

(10.666 - 1) тыс. руб. соответственно. Это

можно подтвердить, подставив в ограничения двойственной задачи оп-

тимальные значения вектора Y.

7-4/3

5-0

2-1/3

= 30/3

=10

>3,

2-4/3

8-0

4-1/3

= 12/3=4 = 4,

2.4/3 +

4-0

+ 11/3 = 9/3 = 3 = 3,

6-4/3

+ 3 0 + 8

1/3 = 32/3

=10.666>1.

Разницу между правыми и левыми частями ограничений двойст-

венной задачи можно найти в Отчете по устойчивости в столбце

«Нормируемая стоимость».

Анализ влияния изменения правых частей ограничений на зна-

чения целевой функции (чувствительность решения к изменению запа-

сов сырья) выполняется с помощью теоремы об оценках.

Предположим, что запас сырья ресурса «труд» изменился на 12 ед.,

т.е.

теперь он составляет 80 + 12 = 92 ед. Из теоремы об оценках

(2.3.11)

известно, что колебание величины

Ь,

приводит к увеличению или

уменьшению

fiX).

Оно определяется величиной у, в случае, когда при

изменении величин

Ь,

значения переменных у, в оптимальном плане со-

ответствующей двойственной задачи остаются неизменными. В нашей за-

даче увеличение запасов ресурса «труд» приведет к увеличению значения

целевой функции на 16 тыс. руб.

(А/(х)

Д£м

•

>'i

= 12 • 4/3 = 16). Для

двойственных оценок оптимального плана весьма существенное значе-

ние имеет их предельный характер. Точной мерой влияния ограничений

на функционал оценки являются лишь при малом приращении ограничения.

Известно, что оценки не меняют своей величины, если не меняется набор

векторов, входящих в базис оптимального

плана,

тогда как интенсивности

этих векторов (значения неизвестных) в плане могут меняться.

Поэтому необходимо знать такие интервалы изменения каждого из

свободных членов системы ограничений исходной ЗЛП, или интервалы

устойчивости двойственных оценок, в которых оптимальный план двой-

ственной задачи не менялся бы. Эту информацию можно получить из

Отчета по

устойчивости.

В нашей задаче в нижеприведенном фраг-

менте отчета видно, что запасы дефицитных ресурсов «труд» и «обору-

дование» могут быть как уменьшены, так и увеличены, увеличение запа-

са ресурса «сырье» не повлияет на план выпуска продукции.

Ограничение

правая часть

480

130

Допустимое

увеличение

150

1Е+30

Доп)

стичое

уменьшение

200

После увеличения запаса ресурса «труд» до 92 чел./ч было получено

новое решение задачи. Изменение запасов ресурсов в пределах интерва-

лов устойчивости двойственных оценок привело не только к изменению

значения целевой функции на 16 тыс. руб., но и к изменению плана вы-

пуска. При этом структура плана не изменилась - изделия, которые были

убыточны, не вошли и в новый план выпуска, так как цены на ресурсы

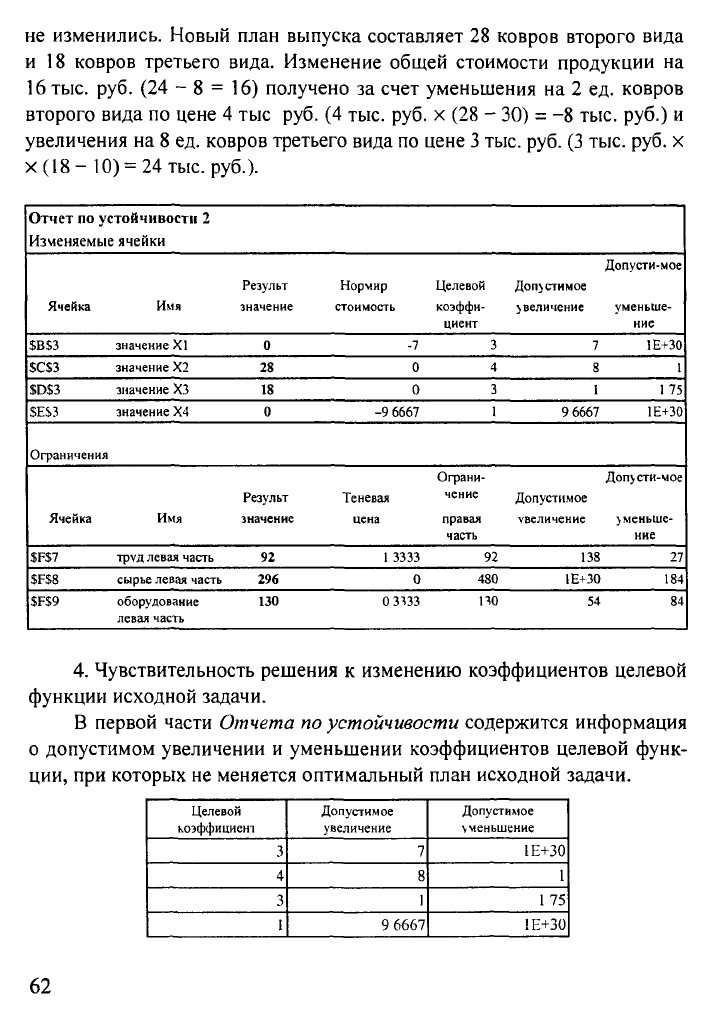
не изменились. Новый план выпуска составляет 28 ковров второго вида

ковров третьего вида. Изменение общей стоимости продукции

на

тыс. руб.

(24 - 8 =

16)

получено

за

счет уменьшения

на 2

ед. ковров

второго вида по цене

тыс руб. (4 тыс. руб.

(28

30) =

-8

тыс. руб.)

увеличения на

ед. ковров третьего вида по цене

тыс. руб. (3 тыс. руб.

х (18-10)

тыс. руб.).

Отчет

по

Изменяем

Ячейка

$в$з

$с$з

$D$3

$Е$3

устойчивости

ые ячейки

Имя

значение

значение Х2

значение ХЗ

значение Х4

Ограничения

Ячейка

$F$7

$F$8

$F$9

Имя

труд левая часть

сырье левая часть

оборудование

левая часть

Результ

значение

Результ

значение

296

130

Нормир

стоимость

-7

-9 6667

Теневая

цена

1 3333

озззз

Целевой

коэффи-

циент

Ограни-

чение

правая

часть

480

ПО

Допустимое

величение

9 6667

Допустимое

увеличение

138

1Е+30

Допусти-мое

уменьше-

ние

1Е+30

175

1Е+30

Допусти-чое

меньше-

ние

184

Чувствительность решения

изменению коэффициентов целевой

функции исходной задачи.

В первой части

Отчета

по

устойчивости

содержится информация

о допустимом увеличении

уменьшении коэффициентов целевой функ-

ции, при которых не меняется оптимальный план исходной задачи.

Целевой

коэффициент

Допустимое

увеличение

9 6667

Допустимое

уменьшение

1Е+30

175

1Е+30

2.4.

ТРАНСПОРТНАЯ ЗАДАЧА

Транспортная задача является одной из наиболее распространенных

задач линейного программирования и находит широкое практическое

приложение.

Постановка транспортной

задачи.

Некоторый однородный продукт,

сосредоточенный у т поставщиков

Л,

в количестве

{

1,..., т) единиц,

необходимо доставить п потребителям В, в количестве

= 1, ..., п) ед.

Известна стоимость

перевозки единицы груза от г-го поставщика

ку'-му

потребителю.

Необходимо составить план перевозок, позволяющий вывести все

грузы, полностью удовлетворить потребности и имеющий минимальную

стоимость.

Сформулируем экономико-математическую

модель транспортной

задачи. Обозначим через

количество единиц груза, запланированных

к перевозке от /-го поставщика к

j-му

потребителю. Так как от

i-ro

по-

ставщика

у'-му

потребителю запланировано к перевозке

единиц гру-

за, то стоимость перевозки составит

х,

Стоимость всего плана выразится двойной суммой

т п

2J2J

Систему ограничений получаем из следующих условий задачи:

а) все грузы должны быть перевезены, т.е.

Х*!/

=а

\,...,m,

7=1

б) все потребности должны быть удовлетворены, т.е.

*!/=£;.

j =

\,...,n.

/=1

Таким образом, математическая модель транспортной задачи имеет

следующий вид: найти минимальное значение линейной функции

т п

= ll

v (2-

)

i=ly=l

при ограничениях

£x

=a,

i =

],...,

т;

(2.4.2)

7=1

Y.x,j=bj,

l....,n;

(2.4.3)

(=1

>0,

\,...,m,

\,...,n.

(2.4.4)

В рассмотренной модели предполагается, что суммарные запасы

равны суммарным потребностям, т.е.

т п

X*.

= XV (2-4.5)

1=1 у=1

Транспортная задача, в которой суммарные запасы и потребности

совпадают, т.е. выполняется условие (2.4.5), называется закрытой моде-

лью;

в противном случае - открытой. Для открытой модели может быть

два случая:

а) суммарные запасы превышают суммарные потребности

X*,

Ibj,

/=1

у=1

б) суммарные потребности превышают суммарные запасы

т п

x°.>xv

»=1

7=1

Линейная функция одинакова в обоих случаях, изменяется только

вид системы ограничений.

Найти минимальное значение линейной функции

^ ~

2^ 2^

^у

i=U=i

при ограничениях

7=1

l—,n,

>0;

, -

(случаи а)

(случай б)

h--,n,

X,j

>0.

Открытая модель решается приведением к закрытой модели.

В случае а, когда суммарные запасы превышают суммарные по-

требности, вводится фиктивный потребитель

В„+\,

потребность которого

т п

Vi^X^-X^

•

1=1 у=1

В случае б, когда суммарные потребности превышают суммарные

запасы, вводится фиктивный поставщик

т+

запасы которого

п т

i=l

Как стоимость перевозки единицы груза до фиктивного потребите-

ля,

так и стоимость перевозки груза от фиктивного поставщика полага-

ются равными нулю, так как груз в обоих случаях не перевозится.

Транспортная задача имеет п

+ т

уравнений с т

•

п неизвестными.

Матрицу X =

)

„,

удовлетворяющую условиям (2.4.2) - (2.4.4),

называют планом перевозок транспортной задачи

(^„-перевозками).

План X*, при котором целевая функция (2.4.1) обращается в мини-

мум,

называется оптимальным.

Решение транспортной задачи

с помощью средства EXCEL «Поиск решения»

Исходные данные транспортной задачи приведены схематически:

внутри прямоугольника заданы удельные транспортные затраты на пере-

возку единицы груза

(с,

;

слева указаны мощности поставщиков

(a,-),

сверху - мощности потребителей

(ty).

Найти оптимальный план закреп-

ления поставщиков за потребителями

(*,,).

Мощности

поставщиков

320

100

Мощности потребителей

250

100

150

В данной задаче суммарные запасы равны суммарным потребно-

стям, т.е.

2>,

2>7=550.

1=1 7=1

Транспортная задача, в которой суммарные запасы и потребности

совпадают, является закрытой.

Ввод условий задачи

состоит из следующих основных шагов:

Создание формы для ввода условий задачи.

Ввод исходных данных.

Ввод зависимостей из математической модели.

Назначение целевой функции.

Ввод ограничений и граничных условий.

А В С D Е

,•3

-9

Матриц!

—

перевозок (изменяемые ячейки)

1 1

Исходные данные

320

100

250

100

150 50

1 4

9: 9

*v'--,!?'•••.

Рис.

2.4.1.

Создание формы для

ввода условий

задачи.

Изменяемые ячейки - ВЗ:Е6. В эти ячейки будет записан опти-

мальный план перевозок -

ху.

Введены исходные данные задачи.

'." :,::.::'

Установить целевую

ячейку:

]$в$15vj

Равной:

максимальному значению

С"

качению:

^полнить

Закрыть

минимальному значению

изменяя

ячейки;—;——

|$В$3:$Е$б

щ*раничения;

мп.тя

$А$3:$А$6

$А$10:$А$13

•1$В$7:$Е$7

$Б$9:$Е$9

Предположить

Добавить

Параметры

Восстановить

Справка

Рис.

2.4.2.

Введены

зависимости

из математической

модели.

Выражение для

вычисления

значения

целевой функции получено с помощью функции

СУММПРОИЗВ(ВЗ:Е6,ВЮ:Е13).

••:•

.."""iji'?.-:

Установить целевую ячейку:

j$B$15_Vj

Равной:

максимальному

значению

минимальному

значению

г Мзменая

ячейки:

—

! | •

—.

1$В$3'$Е$6

Ограничения:-

IIP

значению:

°У Предположить

Выполнить

Закрыть

Параметры

Восстановить

Справка

Рис.

2.4.3.

На экране диалоговое окно

Поиск

решения.

После вызова

Поиска решения

курсор подвести

поле «Установить

целевую ячейку»

ввести адрес: В15. Ввести направление целевой функ-

ции

«минимальному

значению».

Поместить курсор

поле «Изменяя ячей-

ки».

Ввести адреса изменяемых ячеек ВЗ:Е6. Далее следует добавить

ограничения.

D Н

Матрица

перево:

ок (изменяемые»

—t—

•

Исходные

иииые

•ейюО

Сшшнзрйзе

|$А$З$А$6

ijjp"

Ш Отеенз

Ограничение:

•j||=$A$10$A$13

Добавить

Сдада

Рис.

2.4.4. На экране диалоговое окно Добавление ограничения.

Все грузы должны быть перевезены, т.е.

Х%

=а

/, /

1,..,W-A3A6

A1D

A.13.

7=1

i !

F О

i H

Maipmvi

перевозок (изменяемые ячейки)

4 1

J Исходные

л&кные

Сложена эчейсу?

*•

\Щ7 $Е$7

(Ж

Отмена

"3 |=*B*9$EJ9

Дс^ааить

Cppwwta

10'

-12

320

100

, 250

100

150

•щ

IJlmin

"ИЗ!

Рис.

2.4.5. На экране диалоговое окно Добавление ограничения.

Все потребности должны быть удовлетворены, т.е.

1,-..,и-в7а:7=в9а:9.

После ввода последнего ограничения вместо

добавить

ввести ОК. На

экране появится окно Поиск

решения

с введенными ограничениями (см.

рис.

2.4.3).

Решение задачи

Решение задачи производится сразу же после ввода данных, когда

на экране находится диалоговое окно

Поиск

решения (рис. 2.4.3). С по-

мощью окна

Параметры

можно вводить условия для решения оптими-

зационных задач. В нашей задаче следует установить флажок «неотри-

цательные значения» и флажок

«линейная модечъ»

(рис.

2.4.6). Нажать

кнопку ОК. Опять появится диалоговое окно

Поиск

решения.