Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL. Практикум
Подождите немного. Документ загружается.


Исследование остатков полезно начинать с изучения их графика.
Он может показать наличие какой-то зависимости, не учтенной в моде-
ли.
Скажем, при подборе простой линейной зависимости между Y и X
график остатков может показать необходимость перехода к нелинейной
модели (квадратичной, полиномиальной, экспоненциальной) или вклю-
чения в модель периодических компонент.
Выбросы. График остатков (см. далее рис. 4.2.5) хорошо показывает
и резко отклоняющиеся от модели наблюдения - выбросы. Подобным
аномальным наблюдениям надо уделять особо пристальное внимание,
так как их присутствие может грубо искажать значения оценок. Устра-
нение эффектов выбросов может проводиться либо с помощью удаления
этих точек из анализируемых данных (эта процедура называется цензу-
рированием), либо с помощью применения методов оценивания пара-
метров, устойчивых к подобным грубым отклонениям.
Кроме рассмотренных выше характеристик, целесообразно исполь-
зовать коэффициент множественной корреляции (индекс
корреляции)
R,
а также характеристики существенности модели в целом и отдельных ее
коэффициентов:
где
Sg
- сумма квадратов уровней остаточной компоненты;
S
2
y
- сумма квадратов отклонений уровней исходного ряда от его
среднего значения.
Данный коэффициент является универсальным, так как отражает
тесноту связи и точность модели, а также может использоваться при лю-
бой форме связи переменных. При построении однофакторной корреля-
ционной модели коэффициент множественной корреляции равен коэф-
фициенту парной корреляции.
Коэффициент множественной корреляции (индекс
корреляции),
возведенный в квадрат
(/?"),
называется
коэффициентом
детерминации.
R
2
=\-
S*c>
2
Xfr-зо'
(4.1.Ю)
l(y
t
-y
t
)
2
К*-JO
2
100

Он показывает долю вариации результативного признака, находя-
щегося
под
воздействием изучаемых факторов,
т.е.
определяет, какая
доля вариации признака
Y
учтена
в
модели
и
обусловлена влиянием
на
него факторов.
В многофакторной регрессии добавление дополнительных объяс-
няющих переменных увеличивает коэффициент детерминации. Следова-
тельно, коэффициент детерминации должен быть скорректирован
с
уче-
том числа независимых переменных. Скорректированный R~,
или
R
2
,
рассчитывается
так:
Г =
1-о-я
2
)-^-,
п-к-1
где
п -
число наблюдения; к
-
число независимых переменных.
В качестве меры точности применяют несмещенную оценку дис-
персии остаточной компоненты, которая представляет собой отношение
суммы квадратов уровней остаточной компоненты
к
величине
(п-к- 1),
где
к -
количество факторов, включенных
в
модель. Квадратный корень
из этой величины
(S
f
)
называется
стандартной ошибкой
оценки.
Для проверки значимости модели регрессии используется
F-значение,
вычисляемое
как
отношение дисперсии исходного ряда
и
несмещенной
дисперсии остаточной компоненты. Если расчетное значение
с
Vi
=
(п
- 1)
и
Vi
=
(«
- к -
1)
степенями свободы больше табличного
при
заданном
уровне значимости,
то
модель считается значимой:
R
2
/
F
=
=-&
.
(4.1.11)
(l-R
2
)(n-k-\)
Если существует
к
независимых переменных,
то
будет
к
+ 1 коэф-
фициентов регрессии (включая постоянную), отсюда число степеней
свободы составит
п~(к+
1)
или
п-к-].
Целесообразно проанализировать также значимость отдельных
ко-
эффициентов регрессии.
Это
осуществляется
по
r-статистике путем про-
верки гипотезы
о
равенстве нулю
j-ro
параметра уравнения (кроме сво-
бодного члена):
t
aj
=
aj
/S
aj
,
(4.1.12)
101

где
S
ai
- это стандартное (среднее квадратическое) отклонение коэффи-
циента уравнения регрессии а,-.
Величина
S
aj
представляет собой квадратный корень из произведе-
ния несмещенной оценки дисперсии
S
e
и
j-ro
диагонального элемента
матрицы, обратной матрице системы нормальных уравнений.
S
a
,=S
e
-Jb..,
(4.1.13)
ч
2
5>(0
,
т
-1
где
S
e
=J,—
,
bjj
-диагональный элемент матрицы (X X) .
I
П.
~~~
К
~~~
I
Если расчетное значение
f-критерия
с (п - к - 1) степенями свободы
превосходит его табличное значение при заданном уровне значимости,
коэффициент регрессии считается значимым. В противном случае фак-
тор,
соответствующий этому коэффициенту, следует исключить из мо-
дели (при этом ее качество не ухудшится).
Оценка влияния отдельных факторов на основе модели на
зависимую переменную (коэффициенты эластичности
и
р-коэффициенты)
Важную роль при оценке влияния факторов играют коэффициенты
регрессионной модели. Однако непосредственно с их помощью нельзя
сопоставить факторы по степени их влияния на зависимую переменную
из-за различия единиц измерения и разной степени колеблемости. Для
устранения таких различий при интерпретации применяются средние
частные
коэффициенты эластичности Э(/)
и
^-коэффициенты
/?(/),
ко-
торые рассчитываются соответственно по формулам:
3(j) =
a(j)X
cp
/Y
cp
;
(4.1.14)
№) =
aU)-Sx,fS
y
,
(4.1.15)
где
5
V/
- среднее квадратическое отклонение
фактора/
Коэффициент эластичности показывает, на сколько процентов из-
меняется зависимая переменная при изменении
факторау
на 1%. Однако
он не учитывает степень колеблемости факторов.
102

Бета-коэффициент показывает, на какую часть величины среднего
квадратического отклонения
S,
изменится зависимая переменная
У
с из-
менением соответствующей независимой переменной
X,
на величину
своего среднего квадратического отклонения при фиксированном на по-
стоянном уровне значении остальных независимых переменных.
Указанные коэффициенты позволяют проранжировать факторы по
степени влияния факторов на зависимую переменную.
Долю влияния фактора в суммарном влиянии всех факторов можно
оценить по величине
дельта-коэффициентов
А(/):
Д(;) =
Г
>У
РО-)/Л
2
,
где
г
у
- коэффициент парной корреляции между фактором
у
(/'
= 1, ..., т)
и зависимой переменной.
Использование многофакторных моделей
для анализа и прогнозирования развития экономических систем
Одна из важнейших целей моделирования заключается в прогнози-
ровании поведения исследуемого объекта. Обычно термин «прогнозиро-
вание» используется в тех ситуациях, когда требуется предсказать со-
стояние системы в будущем. Для регрессионных моделей он имеет, од-
нако,
более широкое значение. Как уже отмечалось, данные могут не
иметь временной структуры, но и в этих случаях вполне может возник-
нуть задача оценить значение зависимой переменной для некоторого на-
бора независимых, объясняющих переменных, которых нет в исходных
наблюдениях. Именно в этом смысле - как построение оценки зависимой
переменной - и следует понимать прогнозирование в эконометрике.
Проблема прогнозирования имеет много различных аспектов.
Можно различать точечное и интервальное прогнозирование. В первом
случае оценка - это конкретное число, во втором - интервал, в котором
истинное значение переменной находится с заданным уровнем доверия.
Кроме того, для временных рядов при нахождении прогноза существен-
но наличие или отсутствие корреляции по времени между ошибками.
При использовании построенной модели для прогнозирования де-
лается предположение о сохранении в период прогнозирования сущест-
вовавших ранее взаимосвязей переменных.
103

Для прогнозирования зависимой переменной на
/
шагов вперед не-
обходимо знать прогнозные значения всех входящих в нее факторов. Их
оценки могут быть получены на основе временных экстраполяционных
моделей или заданы пользователем. Эти оценки подставляются в мо-
дель,
и получаются прогнозные оценки.
Построение точечных и интервальных прогнозов на основе регрес-
сионной модели. Какие факторы влияют на ширину доверительного ин-
тервала? Для того, чтобы определить область возможных значений ре-
зультативного показателя, при рассчитанных значениях факторов следу-
ет учитывать два возможных источника ошибок: рассеивание наблюде-
ний относительно линии регрессии и ошибки, обусловленные математи-
ческим аппаратом построения самой линии регрессии. Ошибки первого
рода измеряются с помощью характеристик точности, в частности, вели-
чиной
Sy.
Ошибки второго рода обусловлены фиксацией численного
значения коэффициентов регрессии, в то время как они в действительно-
сти являются случайными, нормально распределенными.
Для линейной модели доверительный интервал рассчитывается
следующим образом. Оценивается величина отклонения от линии рег-
рессии (обозначим ее буквой
U):
U(D =
Syt
Kp
Jv^,
где
Х
ар
=(Хц
п+
1),
Х2(
п+
1),..-,
Х,ф
+
1)).
Для модели парной регрессии формула (4.1.16) принимает вид:
J
l
(X(n
+
l)-X
CD
)
2
"
^{Х,-Х
ср
)
2
Коэффициент
t
a
является табличным значением
f-статистики
Стью-
дента при заданном уровне значимости а и числа наблюдений, / - пери-
од прогнозирования. Если исследователь задает вероятность попадания
прогнозируемой величины внутрь доверительного интервала, равную
70%,
то
t
a
= 1.05. Если вероятность составляет 95%, то
t
a
= 1.96, а при
99%
f„
= 2.65.
104
(4.1.16)
(4.1.17)
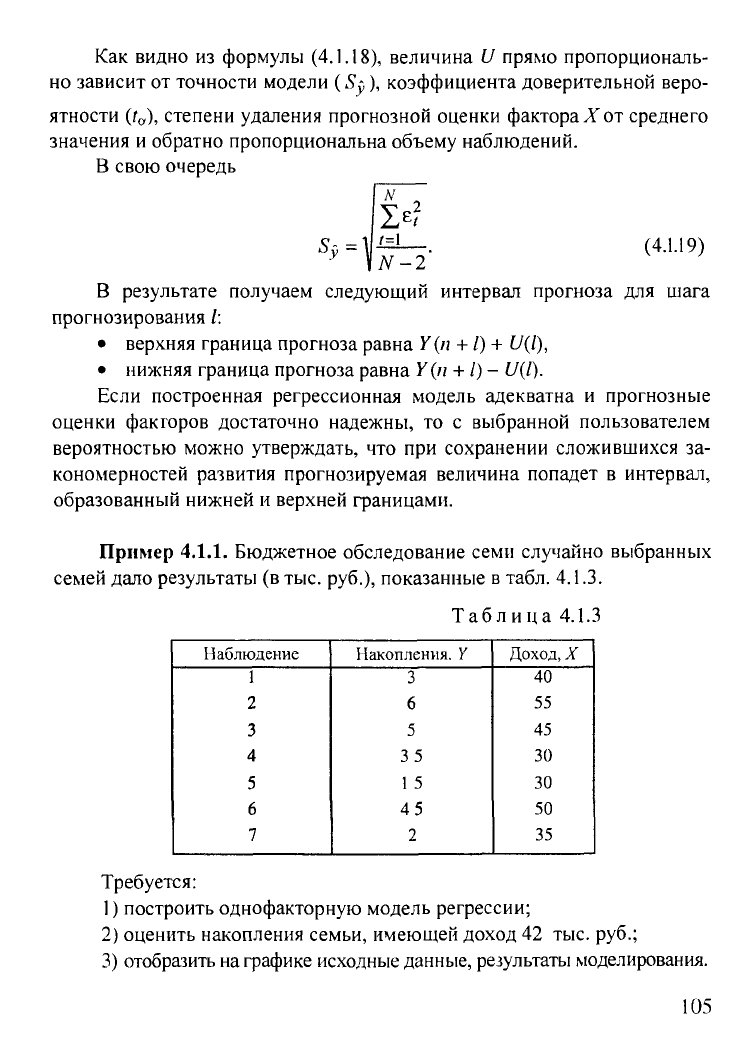
Как видно из формулы (4.1.18), величина U прямо пропорциональ-
но зависит от точности модели
(S
y
),
коэффициента доверительной веро-
ятности
(/„),
степени удаления прогнозной оценки фактора
Хот
среднего
значения и обратно пропорциональна объему наблюдений.
В свою очередь
(4.1.19)
N-2
В результате получаем следующий интервал прогноза для шага
прогнозирования
/:
• верхняя граница прогноза равна Y(n + /) + U(l),
• нижняя граница прогноза равна Y(n
+ I)
- U(l).
Если построенная регрессионная модель адекватна и прогнозные
оценки факгоров достаточно надежны, то с выбранной пользователем
вероятностью можно утверждать, что при сохранении сложившихся за-
кономерностей развития прогнозируемая величина попадет в интервал,
образованный нижней и верхней границами.
Пример
4.1.1.
Бюджетное обследование семи случайно выбранных
семей дало результаты (в тыс. руб.), показанные в табл.
4.1.3.
Таблица
4.1.3
Наблюдение
1
2
3
4
5
6
7
Накопления. Y
3
6
5
35
1 5
45
2
Доход, X
40
55
45
30
30
50
35
Требуется:
1)
построить однофакторную модель регрессии;
2) оценить накопления семьи, имеющей доход 42 тыс. руб.;
3) отобразить на графике исходные данные, результаты моделирования.
105
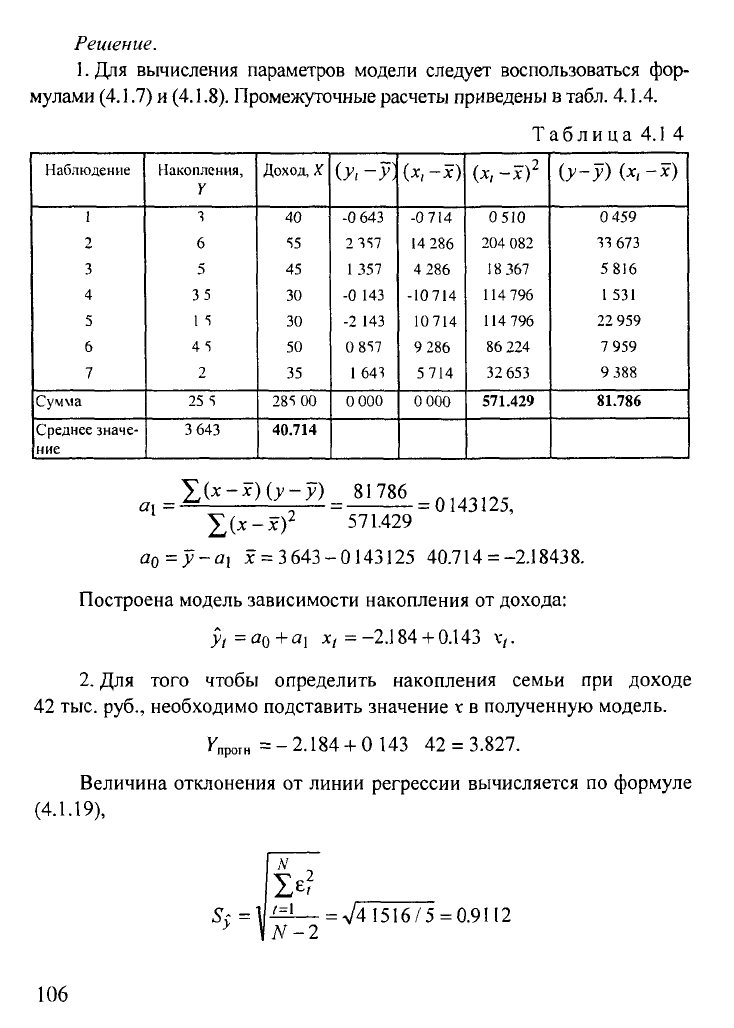
Решение.
1.
Для вычисления параметров модели следует воспользоваться фор-
мулами
(4.1.7) и
(4.1.8).
Промежуточные расчеты приведены в
табл.
4.1.4.
Наблюдение
1
2
3
4
5
6
7
Сумма
Среднее значе-
ние
Накопления,
Y
3
6
5
35
1 5
45
2
25 5
3 643
Доход, X
40
55
45
30
30
50
35
285 00
40.714
(у, -у.
-0 643
2 357
1357
-0 143
-2 143
0 857
1 643
0 000
(х,-х)
-0 714
14
286
4
286
-10714
10714
9 286
5714
0 000
Т
(х,
-х)
2
0510
204 082
18
367
114
796
114
796
86 224
32 653
571.429
аблица4.14
(У
~У) (х,-х)
0 459
33
673
5 816
1
531
22 959
7 959
9 388
81.786
^(х-х)(у-у)
81786
Л]
.-
0
<
а
х
=
— - = =
0143125,
Х(х-Зс)
2
571
-
429
а
0
=у-а
х
х = 3643-0143125 40.714 =
-2.18438.
Построена модель зависимости накопления от дохода:
у,=а
0
+щ
JC,
=-2.184
+
0.143
х,.
2.
Для того чтобы определить накопления семьи при доходе
42 тыс. руб., необходимо подставить значение х в полученную модель.
Кпрогн
= - 2.184 + 0 143 42 = 3.827.
Величина отклонения от линии регрессии вычисляется по формуле
(4.1.19),
lie?
Si =
\\
-^—
= V41516/5 =
0.9112
N -
2
106
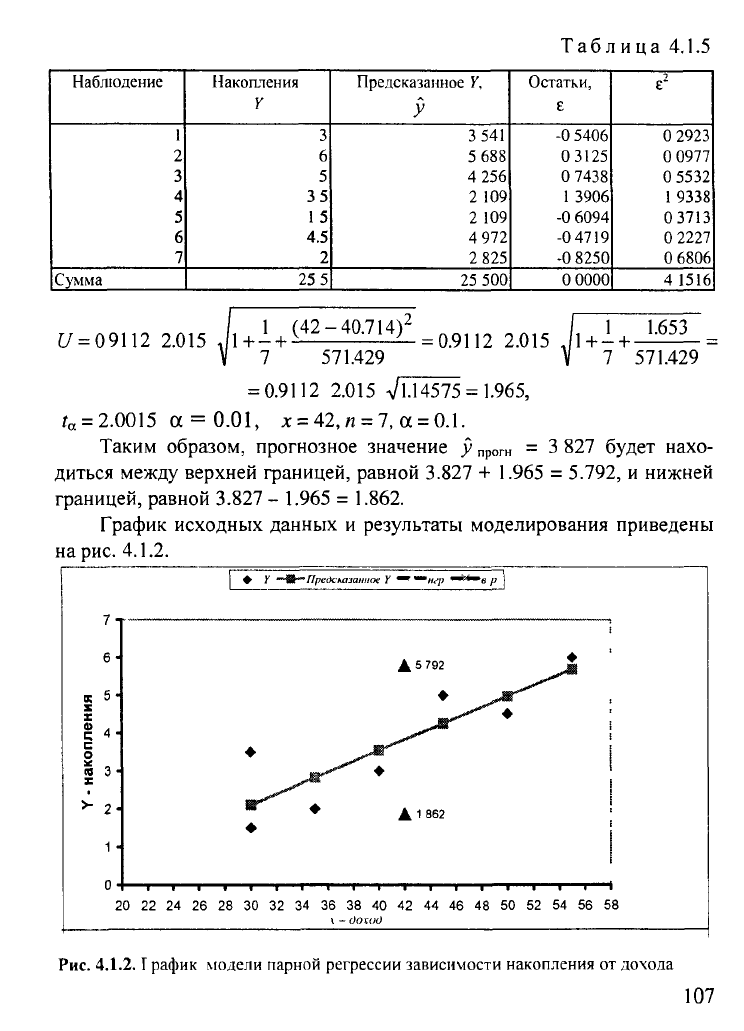
Таблица
4.1.5
Наблюдение
1
2
3
4
5
6
7
Сумма
Накопления
Y
3
6
5
35
15
4.5
2
25
5
Предсказанное
Y,
У
3 541
5 688
4 256
2 109
2 109
4 972
2 825
25
500
Остатки,
е
-0
5406
0 3125
0 7438
1 3906
-0
6094
-0
4719
-0
8250
0 0000
V
0 2923
0 0977
0 5532
1 9338
0 3713
0 2227
0 6806
4 1516
С/
=
09112
2.015
1|1 +
1
+
(42-40.714)-
=09112
l+
!
+
J^L
7 571.429
V 7
571.429
= 0.9112
2.015
л/1.14575
=
1.965,
t
a
= 2.0015
а =
0.01,
х
= 42,и =
7,а
= 0.1.
Таким образом, прогнозное значение
у
пр0
гн
=
3
827 будет нахо-
диться между верхней границей, равной 3.827
+
1.965
=
5.792,
и
нижней
границей, равной 3.827
-
1.965
=
1.862.
График исходных данных
и
результаты моделирования приведены
на
рис.
4.1.2.
•
У
"ЧИН"Предсказанное
У
ят тт
нгр ^**^e
p
7
Т
6-
х
Ф
С
с
о
со
3
•
>
2-
1
•
А 5
792
А 1 862
i
I I 1 1 1 I I I I I I I I I I I I I I
20
22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58
i
-
доход
Рис.
4.1.2.
График
модели парной регрессии зависимости накопления от дохода
107
4.2.
ТЕХНОЛОГИЯ РЕШЕНИЯ ЗАДАЧ
КОРРЕЛЯЦИОННОГО
И
РЕГРЕССИОННОГО АНАЛИЗА
С
ПОМОЩЬЮ ПАКЕТА АНАЛИЗА
Пакет анализа
- это
надстройка, которая представляет широкие
возможности для проведения статистического анализа.
Установка средств
Пакет
анализа.
В стандартной конфигурации программы EXCEL вы
не
найдете сред-
ства
Пакет
анализа.
Даже если установить
их с
компакт-диска EXCEL'97
(или Office'97), они не появятся в меню до тех
пор,
пока вы
не
установите их
в качестве надстройки Excel. Для этого выполните следующие действия:
1.
Выберите команду Сервис
^Надстройки.
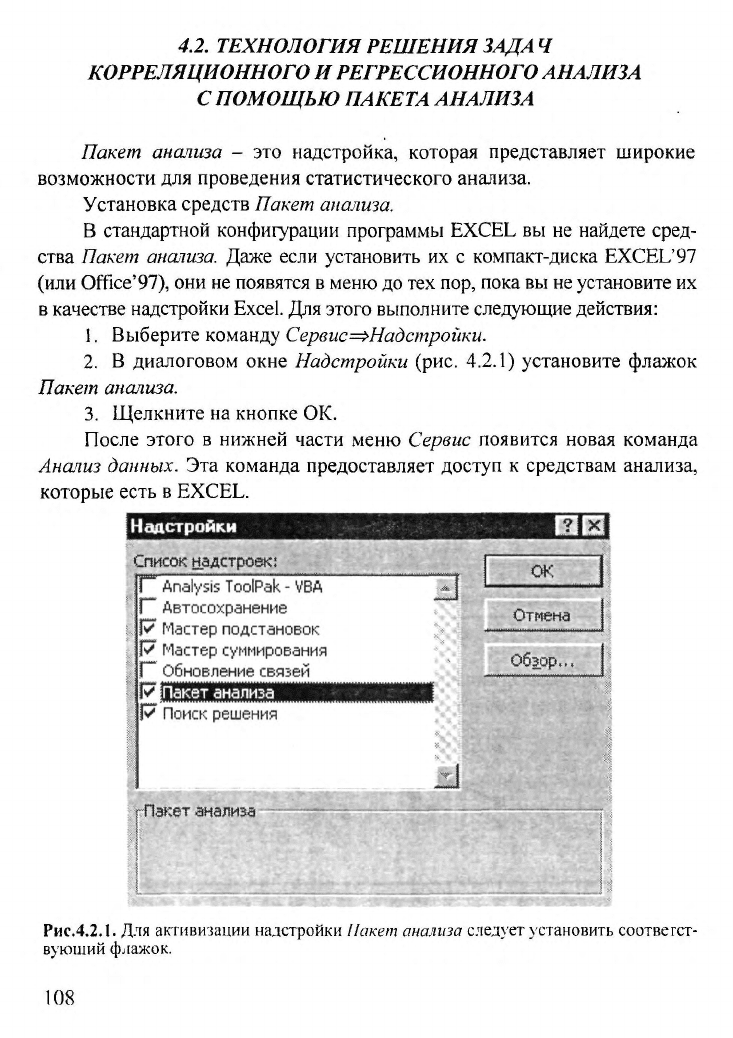
2.
В
диалоговом окне Надстройки (рис. 4.2.1) установите флажок
Пакет анализа.
3.
Щелкните на кнопке ОК.
После этого
в
нижней части меню Сервис появится новая команда
Анализ данных. Эта команда предоставляет доступ
к
средствам анализа,
которые есть в EXCEL.
Надстройки
Список надстроек:
Г"
Analysis
ToolPak
-
VBA
Г"
Автосохранение
Р"
Мастер подстановок
W
Мастер суммирования
Г"
Обновление
связей
ф
Поиск решения
ОК
LJ
Отмена
Обзор.,
ш
*»
I
Г
Пакет анализа
Рис.4.2.1.
Для активизации надстройки Пакет анализа следует установить соответст-
вующий флажок.
108
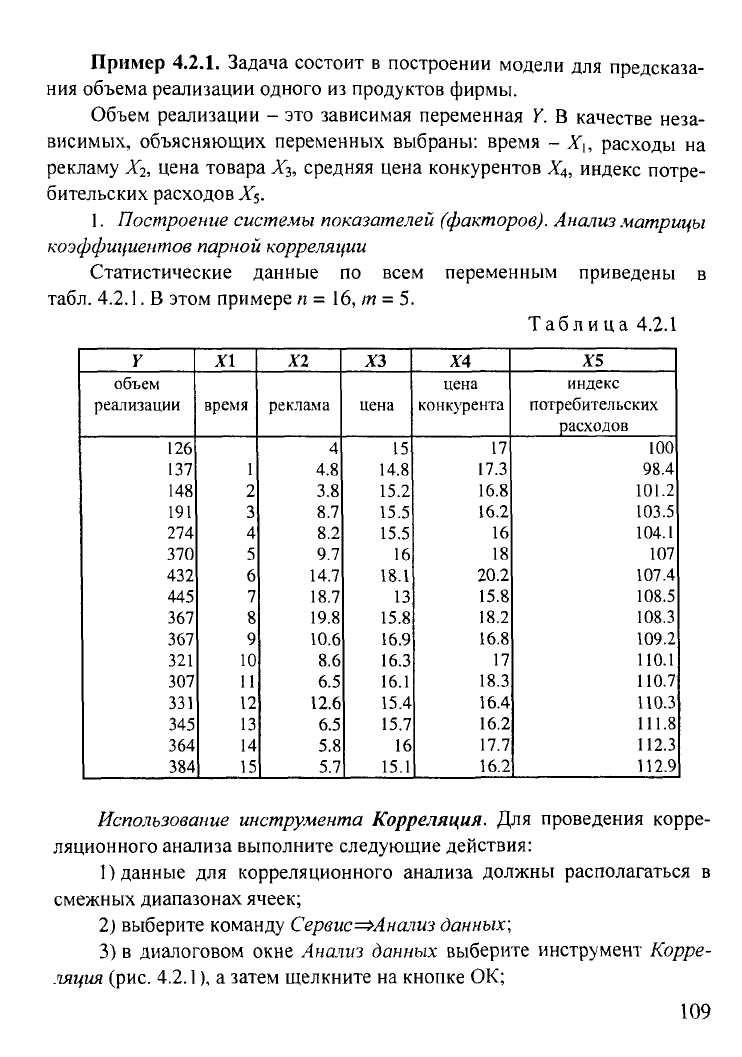
Пример 4.2.1. Задача состоит в построении модели для предсказа-
ния объема реализации одного из продуктов фирмы.
Объем реализации - это зависимая переменная Y. В качестве неза-
висимых, объясняющих переменных выбраны: время -
Х
и
расходы на
рекламу
Х
2
,
цена товара
Хъ,
средняя цена конкурентов
Х
4
,
индекс потре-
бительских расходов
Х
5
.
1.
Построение системы показателей
(факторов).
Анализ матрицы
коэффициентов
парной
корреляции
Статистические данные по всем переменным приведены в
табл.
4.2.1.
В этом примере п = 16, т = 5.
Таблица
4.2.1
Y
объем
реализации
126
137
148
191
274
370
432
445
367
367
321
307
331
345
364
384
XI
время
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Х2
реклама
4
4.8
3.8
8.7
8.2
9.7
14.7
18.7
19.8
10.6
8.6
6.5
12.6
6.5
5.8
5.7
ХЪ
цена
15
14.8
15.2
15.5
15.5
16
18.1
13
15.8
16.9
16.3
16.1
15.4
15.7
16
15.1
Х4
цена
конкурента
17
17.3
16.8
16.2
16
18
20.2
15.8
18.2
16.8
17
18.3
16.4
16.2
17.7
16.2
Х5
индекс
потребительских
расходов
100
98.4
101.2
103.5
104.1
107
107.4
108.5
108.3
109.2
110.1
110.7
110.3
111.8
112.3
112.9
Использование инструмента
Корреляция.
Для проведения корре-
ляционного анализа выполните следующие действия:
1)
данные для корреляционного анализа должны располагаться в
смежных диапазонах ячеек;
2) выберите команду
Сервис =>Анализ
данных;
3) в диалоговом окне Анализ данных выберите инструмент Корре-
ляция
(рис.
4.2.1),
а затем щелкните на кнопке
ОК;
109
