Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

FIRST-ORDER QUASILINEAR SYSTEMS

u=v=0 ony=O

have no analytic solution in a neighbourhood of y = 0 unless f is real and analytic.

To see this, note that u - f + iv is an analytic function whose real part is -f on

y = 0 and whose imaginary part is zero on y = 0.

This is already a striking result, but it only ensures non-existence of solutions

of (2.61) locally near y = 0. However, it is the starting point for H. Lewy's famous

demonstration that, even though f (x, y, t) may be CIO at every point in R3, the

linear partial differential equation

- 2i(x+iy)

= f (x, y, t)

8x+ay

has no solution at all unless f is in addition analytic. The details are too lengthy

to reproduce here and we refer any reader who wishes to see the futility of trying

to construct an all-embracing theory of partial differential equations to (23, 36].

Exercises

2.1. Show that, if ry = 2 and p/p2 is constant, the gasdynamic equations (2.3) and

(2.4) reduce to the shallow water equations (2.1) and (2.2), with p in (2.3)

and (2.4) proportional to h in (2.1) and (2.2).

2.2. Show that when the substitution proposed before (2.8) is made in (2.5)-(2.7)

and squares of barred quantities are neglected, we obtain

T. (Pou+UP)+

y(pov)=0,

=-poe,

Ue =-port.

Show also that

p PO

P P

(1+ \1

-ryPo/)

in this approximation and hence deduce (2.8)--(2.10).

2.3. In a granular material, let the forces on the sides of a rectangle of area baby

be (a, r) by on a side normal to the x axis and (r, ay) bx on a side normal

to the y axis, as in Fig. 2.20. Show that the forces on the diagonal are

cbs = (ayby+Tbx,a.bx+Tby)

and hence that

Now define

or = (ascos0+Tsin0,a.sin0+rcos0).

a2 +a

Vtan 20 =

P=-

as -

ay.

Show that the components of a along and perpendicular to n are

cos 2(t1 - 0) sin 2(r0 r - 0)

-P +

sin 20

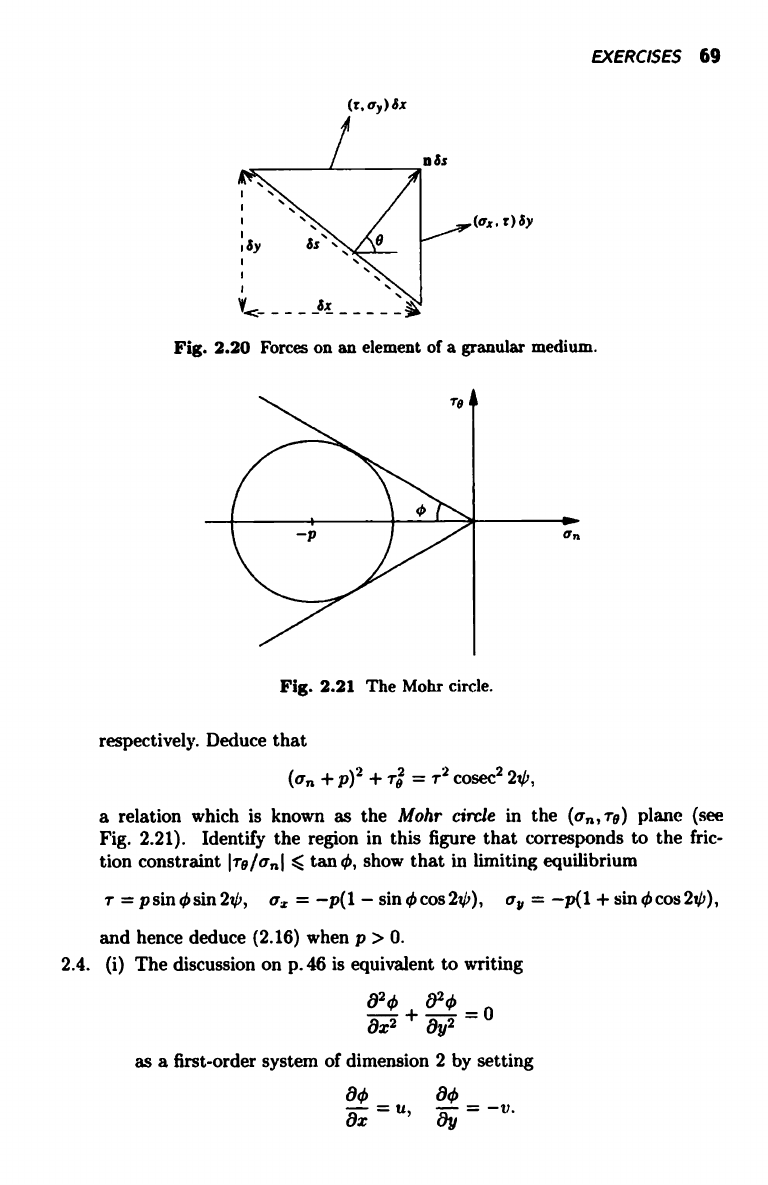
EXERCISES 69

(r, ay) 8x

(17X , T) By

Fig. 2.20 Forces on an element of a granular medium.

Fig. 2.21 The Mohr circle.

respectively. Deduce that

(a + p)2 + rr = r2 cosec2 20,

a relation which is known as the Mohr circle in the (a,,, re) plane (see

Fig. 2.21).

Identify the region in this figure that corresponds to the fric-

tion constraint Ire/anI 5 tan 0, show that in limiting equilibrium

r = psin0sin20, o- f = -p(1 - sin0cos2ji),

a, = -p(1 +sin0cos20),

and hence deduce (2.16) when p > 0.

2.4.

(i) The discussion on p.46 is equivalent to writing

820 02

8x2 + 8y2 -

as a first-order system of dimension 2 by setting

-u.

TO FIRST-ORDER QUASILINEAR SYSTEMS

Can

z z

axe+42+0=0

be written as a system of dimension 2?

(ii) Show that, if A and B are constant matrices and

then

Cul)

can be written as a scalar second-order equation for ul or u2. Would the

same be true for a system with non-constant coefficients A and B?

2.5. Consider the non-autonomous inhomogeneous Cauchy problem

= D(u, x, y) 5j + d(u, x, y),

u=uo onx=O.

8x=0

with

r1=y onx=O

Ot on

Ox Oy

with

t=0 onx=O,

and setting

show that v satisfies the autonomous homogeneous Cauchy problem

with

v=vo onx=O,

where

D 0 d uo

D = OT 0 1

and

vo = 0

OT00 y

EXERCISES 71

2.6.

(i) Show that the solution of

= uay,

with u(0, y) = y, is u = y/(1- x).

(ii) For this example, in the notation of §2.3, d(u) = u and uo(y) = y. What

are R. and Rd? Take pa = pd = p > 0 and show that M. = Md = P.

Deduce that D(U) = p2/(p - U) and Uo(y) = py/(p - y), and hence

that the solution of OU/Ox = D(U) OU/Oy is given implicitly by

_p2x pU

Y= p-U+ p+U'

Deduce that U blows up on the lower branch of the parabola

(1-x±2fx).

The distance from the nearest point on this curve to the origin controls

the radius of convergence of (2.35); how does this distance depend on p?

2.7. Suppose that

+ B

= c,

and A is invertible. Suppose also that the row vector IT is such that

IT (01- 2A-' B) = OT,

(2.62)

where (.,y) is such that (x(t),y(t)) is a characteristic. Show that ITU =

ITA-'ci, which is (2.27).

2.8. Suppose that a hyperbolic system can be written in terms of the Riemann

invariants r1,2 as

8x + A1(rl , r2)

8y)

rl =

(8x + A2 (rl,

r2)

p.. J

r2 = 0.

Show that x and y satisfy the linear system V N /

8r2

= Al(rl,r2)ur2,

2.9. Write the system

in the form

5,1 = A2(rl,r2)iirl .

Ou Ou Ov

F+-0'

+ey+2 + =0,

Ox-ay+2ay=0,

+B-

and show that it is hyperbolic with dy/dx = A = ±1, 3 on the characteristics.

FIRST-ORDER QUASILINEAR SYSTEMS

Find the left eigenvalues of B and obtain the Riemann invariants 3u - v - w,

u-v+w and u+3v+w.

* 2.10. Rearrange (2.3) and (2.4) into the form

0 On

lap ap

+-(pu) =0,

+u-+-- =0, +u-+yp- =0,

at ax

at ax p ax

ax ax

which could also be written as AOu/ax + B au/ay = 0, and show that the

system is hyperbolic and that the characteristic speed dx/dt = A satisfies

A = u or A = u±a, where a2 = 7P /p (a is the sound speed). By multiplying

by suitable row vectors tT satisfying tT (yI - iA-'B) = OT, obtain the

relations

7pp-pP=0, ±ypri-ap=0

on the characteristics, respectively, and deduce that there is one Riemann

invariant, namely p/p"' on dx/dt = u.

Assuming that p/p'' is the same constant everywhere, verify that the quan-

tities u ± 2a/(-t - 1) are constant on dx/dt = u ± a, respectively.

s 2.11. Repeat Exercise 2.10 for the system (2.5)-(2.7) by rearranging the equations

into the form A au/ax + B au/ay = 0, with u = (p, u, v, p) T and

u p 0 0

v 0 p 0

O u 0 1/p

0 v 0 0

0 0 u 0

- 0 0 v

1/p

O yp0 u

OOyp V

Deduce that the characteristic directions are given by dy/dz = A, where

A = v/u (twice) or

-UV ±

a u +v -a

a2=LP.

a2-u2

Show that these results agree with the formulae for A on p.53. Also obtain

the relations

7PP-pP=0

and uu+vv+p =0

on A = v/u, and

yp(Au-v)+(v-Au)p=0

on the other characteristics, and find the Riemann invariants, if any exist.

2.12. Write the system of equations

+ =

1/2

in the form

EXERCISES 73

+ B ji = c.

(2.63)

Assuming that u and v are strictly positive, show the characteristic directions

are given by A = y/i = ±(uv)-112. Show also that the corresponding left

eigenvectors of Exercise 2.7 are (v1/2,±u1/2) and that, when \ = 1/ uv,

(2.27) becomes

Show that the condition

v1/2ie + u1/2iu = 2(uv) 1/2i.

(R) 8u (R)

for (2.27) is satisfied, and finally that

u1/2 + v1/2 = x + constant

on this characteristic.

2.13. The system (2.1) and (2.2), with h proportional to v2, can be written as

+uay+2vOy=0,

2Ox + 2u

ey Oy = 0.

Show that this system is hyperbolic with characteristic directions A = dy/dx

= u ± v, and that u ± 2v are the corresponding Riemann invariants.

If u(0, y) = 0 and v(0, y) is continuous and takes the value 1 in y < 0, show

that u = 0 and v = 1 in x + y < 0, x > 0, assuming that no shocks form.

Show also that, for x + y sufficiently small and positive,

+(32 -1)O u-0,

with u = 0 on x + y = 0. Verify that the equation is satisfied by

2(x + y)

What properties must v(0, y) have for y > 0 for this solution to be relevant?

+2.14. To ease the calculations in Exercise 2.3, set 0 = it/2 and p = -(a. +oy)/2.

Using the relations

T = p sin 20,

tan 20 =

27-

Qz - oy'

show that

a. = -p(1 - cos 2t'),

ay = -p(1 + cos 2,P),

74 FIRST-ORDER QUASILINEAR SYSTEMS

and hence that

where u = (p, ,')' and

_ cos 2t' - I -2p sin

sin 2t/i

2p cos 2t'

sin 20

2p cos 2 , '

- -(1 + cos 20) 2p sin 21 '

Deduce that the system has a double characteristic

dx =

= -

cot t',

on which t¢ is a constant. (If ¢ < 7r/2, it can be shown that the characteristics

split into

ax =

-cot

\OA: (4

2) )

and the Riemann invariants are t/' ± 1 cot 0logp.)

2.15. Suppose that A and r are related to x and t by

A = A(x, t)

and

r = T (t') dt'.

Using the chain rule

8x 8A' a

-+ T

8 + 8t 8A'

show that

8x 8A _ 8z

1 8A

and

-Tax

/0A

Hence eliminate u between (2.11) and (2.12) to show that

82x 82x _ 1 8x

8A2 8A8r

A 8A

2.16. The system

8v 8v

1 Oh

8(h2) 8(h2v) _

8t +

8x h2 8x' 8t + 8x = 0

is an approximate model for a slender axisymmetric inviscid fluid jet of radius

h(x, t) and axial velocity v(x, t), aligned with the x axis. Show that, if x and

t are regarded as functions of v and h, the system becomes

8x at

1 at

h at

8t 8x

Y h-

v 8h

ha 8;

2 8h

- v - + - = 0 .

Show further that eliminating x leads to

EXERCISES 75

2.17. The system (2.3) and (2.4) is derived from the physical conservation laws

OP N

aP+OQ=0

where

(i) P=P,Q=Pu;

(u) P = Pu, Q = P + Pu2;

(iii) P=p/(7-1)+2Pu2,Q=u(p/(7-1)+2pu2)+pu.

Show that the Rankine-Hugoniot relation for a shock moving with speed V

is [Q]± = V [P]+-, and hence from (i) that [pu]± = V [p]+-. Use this with (ii)

and (iii) to deduce the remaining conditions in (2.49).

2.18. Look for a travelling wave solution u(x, y) = U(z), with z = (y - Vx) /E, to

the equation

- (1 \

8x+- nuJ

02u

= E aye

for -oc < z < oo.

Show that

T z-

U" - VU + constant,

and deduce that V = [nU"] oo /[. Show also that, when n = 2, U can

only tend to U(±oo) as z -> too if dU/dz < 0.

Introduction to second-order

scalar equations

3.1

Preamble

In Chapter 2 we tried to describe, in the simplest possible terms, the only reason-

ably general framework that exists concerning the solutions of the Cauchy problem

for arbitrary partial differential equations. Many pages could now be spent in ex-

plaining this framework in more detail, but we will instead devote the next three

chapters to a more specialised analysis of three commonly occurring classes of

second-order scalar equations. This will enable us not only to illustrate as simply

as possible the subtleties that can arise when 'non-hyperbolic' equations are being

solved, but also to look at the role played by the ideas proposed in Chapter 2 when

they are viewed in a more concrete setting.

When we start to consider specific second-order equations in Chapters 4-6,

we will find that we rapidly encounter formidable technical difficulties. Hence this

chapter is a preface that emphasises the central ideas that will need to be kept in

mind in the next three chapters.

Before we start, let us make one elementary observation to illustrate the care

that may have to be taken with what appear to be harmless enough second-order

scalar equations. It comes from a trivial piece of Fourier analysis and shows that the

qualitative behaviour of the solutions of second-order partial differential equations

with Cauchy data is far more diverse than in the case for initial value problems

for second-order ordinary differential equations. In the latter case, the Cauchy-

Picard theorem guarantees existence, uniqueness and continuous dependence on

the data, assuming only appropriate Lipschitz continuity. However, we shall see

that partial differential equations which are on the face of it much smoother can

in fact lose the property of continuous dependence on the Cauchy data. This fact,

which provides one of the basic motivations for trying to classify these partial

differential equations, is illustrated by considering the solutions of the two problems

(i)

au 02u

(3.1)

(ii)

Ox2'

2--

8 22

(3.2)

in y > 0, with data

PREAMBLE 77

u(x, 0) _ E an cosnx

for -oo

< x

< oo.

(3.3)

n=0

We assume that an are such that u(x, 0) has continuous second derivatives, which

clearly demands that an = o(n-2) as n -a co.

Separation of the variables gives the respective solutions as

(i) u =

r `ane-nzYCosnx,

n=0

(ii) u = E

n2 N

Cos nx.

n=0

The series (3.4) has better convergence properties than (3.3) for y > 0, but the

series (3.5) does not even converge unless an decays very rapidly indeed as n -* oo.

For example, even if an = e-"', (3.5) blows up as y -* 1 (if an = e-`"3, f > 0,

blow-up is at y = e, however small that may be, and if an = O(e-`"), as is generic

for periodic analytic functions, there is no solution at all).

Similarly, if we consider the problems

02U

2 =

8zx2

, (3.6)

(iv)

802U 0

8x2

(3.7)

for y > 0, with, for example, data

u(x, 0) = E a. cos nx,

n=0

the Fourier series solutions are

(iii)

E an cos ny cos nx,

n=0

(x, 0) = 0,

E an cosh ny Cos nx,

n=0

(3.10)

respectively, and a similar contrast can be drawn to that between (3.4) and (3.5).

The switch from (3.6) to (3.7) can easily occur in practice, as has been an-

ticipated on p.42. Suppose that we have an `irrotational' solution of the system

(2.8)-(2.10) describing linearised steady gas dynamics, so that (6i, u) = V O. Elim-

inating p gives

U al

a z

((

\1-

/8x2+Oy2-0;

(3.11)

depending whether the Mach number U/ao is greater or less than unity, we are

effectively led to (3.6) or (3.7), respectively. In fact, the derivation of (3.11) breaks