Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations
Подождите немного. Документ загружается.


58
FIRST-ORDER QUASILINEAR SYSTEMS
and the characteristic directions on the shock y = x/2 have slope zero in y < x/2
and unity in y > x/2, as in Fig. 2.11. They are therefore both outgoing so that
k = 2 > n - 1; the causality condition rejects this solution (we could indeed
construct many such inadmissible shocks). In fact, this argument applies to all the
weak solutions that we could find that satisfy the Rankine-Hugoniot relations with
a shock of non-zero strength. Hence there are no causal discontinuous solutions
and the continuous solution
0, y < 0,
u=
y/x,
0'< y<x,
1,
x < y,
which is automatically causal, is the only acceptable solution to the Cauchy prob-
lem.
Now let us look at the case
Un =
0, y > 0,
I, y <0
(2.48)
A solution, indeed the only one satisfying the Rankine-Hugoniot relations, is
u=
0, y > x/2,
1, /2V < x ;
the characteristic directions on the shock have slope zero in y > x/2 and unity
in y < x/2, as in Fig. 2.12. They are therefore both incoming, that is they both
intersect x = 0, and hence k = 0. Thus k = n - 1 and this is indeed the unique
appropriate causal solution.
This example paves the way for a more complete discussion of gasdynamic
shock waves. The models (2.3)-(2.7) are already in conservation form and the jump
conditions determined from (2.45) represent the well-known Rankine-Hugoniot
Y
Fig. 2.11 Solution of (2.46) and (2.47) with too many outgoing characteristics.

WEAK SOLUTIONS AND SHOCK WAVES 59
Y
-> r
Fig. 2.12 Causal solution of (2.46) and (2.48).
relations for gasdynamic shocks. For a one-dimensional shock moving with speed
V the result of applying (2.45) to (2.3) and (2.4) can be manipulated to yield
[p(V - u)]± = 0,
[p + p(V - U)2]1 = 0,
[_-p
-1)p +
2(`'
-
u)2J o,
(2.49)
corresponding to conservation of mass, momentum and energy, respectively (see
Exercise 2.17). For the existence of a shock, with [p]± 36 0, separating two regions
in the (z, t) plane in which the flow variables are constant, it can be shown further
that the flow must pass through a `compressive shock', across which p and p
increase, if it is to be modelled by a causal weak solution. Figure 2.13 shows the
(z, t) plane for (2.3) and (2.4) corresponding to a piston z = Vt driving a gas
in x > Vt. For V > 0 we have n = 3 and the causal weak solution has k = 2.
However, this value of k cannot be attained when V < 0, and thus no 'expansion
shock' appears in this case.
A similar argument can be applied to the two-dimensional system (2.5)-(2.7)
and, after lengthy algebra, it emerges that two possible Rankine-Hugoniot shocks
can 'bend' a prescribed supersonic stream around a corner, as in Fig. 2.14. Now
n = 4 (although one characteristic is double) and the appropriate weak solution
has k = 3; the shock with the smaller slope is the physically acceptable solution,
as is readily observed in wind tunnels.25
2.5.2 Viscosity and entropy
Causality is just one kind of mathematical filter that can be introduced in an effort
to try to render weak solutions of conservation laws unique. Two other methods
25We remark that other `shocks' that satisfy the Rankine-Hugoniot relation are possible. For
example, it is possible to satisfy (2.49) with [p]± = 0, [u)± = 0, u = U and [p)± # 0, and this is
called a contact discontinuity. For the two-dimensional system (2.5)-(2.7) the analogous shock
has a jump in density and tangential velocity and it is called a vortex sheet, a concept to which
we will return in Chapter 7. Both these `shocks' are degenerate in that they coincide with one
of the characteristics.
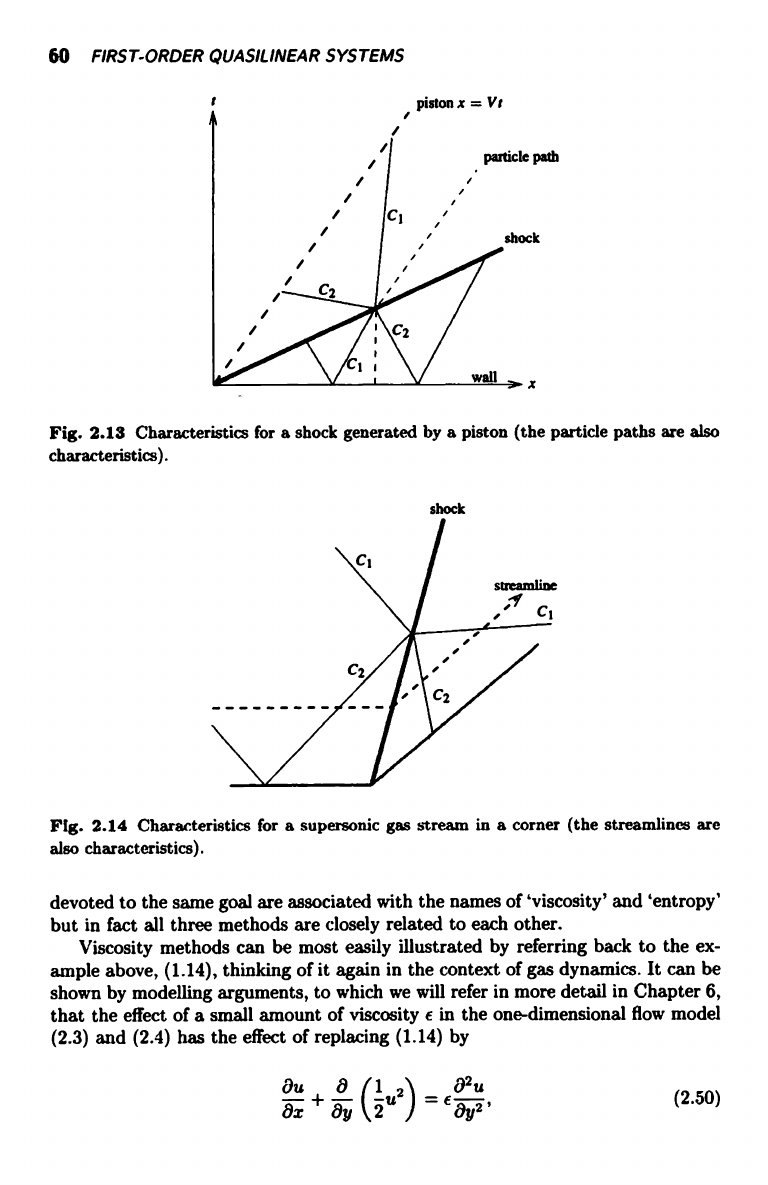
60
FIRST-ORDER QUASILINEAR SYSTEMS
Fig. 2.13 Characteristics for a shock generated by a piston (the particle paths are also
characteristics).
Fig. 2.14 Characteristics for a supersonic gas stream in a corner (the streamlines are
also characteristics).
devoted to the same goal are associated with the names of `viscosity' and `entropy'
but in fact all three methods are closely related to each other.
Viscosity methods can be most easily illustrated by referring back to the ex-
ample above, (1.14), thinking of it again in the context of gas dynamics. It can be
shown by modelling arguments, to which we will refer in more detail in Chapter 6,
that the effect of a small amount of viscosity e in the one-dimensional flow model
(2.3) and (2.4) has the effect of replacing (1.14) by
2
8x + 8y
C2u2J - E8y2'
(2.50)

WEAK SOLUTIONS AND SHOCK WAVES 61
U-00
U
-4
U00
y - V.r
Fig. 2.15 Smoothing of a shock by viscosity.
at least as far as relatively small disturbances are concerned.26 As shown in Exer-
cise 2.18, this equation, which is known as Bangers' equation, has solutions that
are travelling waves. These are such that u = U((y-Vx)/e), -co < y-Vx < +oo,
as long as
V =
{U2]:/EU];
this is just the condition that the Rankine-Hugoniot conditions are satisfied by
the asymptotic values of u far `upstream' and `downstream' of the shock wave.
The shock has been smeared out over a region in which y - V x is of order a by
the presence of the viscosity, as in Fig. 2.15.
The introduction of viscosity not only retrieves the Rankine-Hugoniot condi-
tions for us, but also still more information is contained in (2.50). The analysis of
Exercise 2.18 shows that, in a travelling wave, U must be a decreasing function of
y - Vx. We will see in Chapter 6 that this has the physical interpretation that the
wave can only be compressive, and hence we have excluded `expansion' shocks, as
likewise did the causality condition for (2.50) with e = 0.
A further idea that is equivalent to causality in this case is that, if (1.14) is
again rewritten as
8 + F (v(u)) = 0,
then the convex function v = Ju2, known as the entropy, has to increase as a result
of the passage of the shock, irrespective of the sign of the shock velocity. Thus an
analogy can be drawn between causal shocks, viscous shocks and shocks across
which a convex function increases. The latter interpretation suggests an analogy
with the concept of entropy that arises in statistical mechanics.
In summary, the theory of weak solutions of hyperbolic conservation laws is
incomplete without the incorporation of extra information. When this information
is introduced in the form of causality, viscosity or entropy arguments, a unique
26Note that the introduction of such a viscosity term into the right-hand side of a conservation
law, which is the result of a modelling assumption, has different consequences depending on the
way in which the law is written; the solution of (2.50) would be quite different if the left-hand side
were 8/8x (Zu2) + 8/ay (.u3); viscosity thus legislates for a particular weak solution, reflecting
the modelling assumption that has been made.

62
FIRST-ORDER QUASILINEAR SYSTEMS
weak solution emerges in which the Rankine-Hugoniot conditions are satisfied
across any shock waves that are present. The concept of viscosity is a stronger
one than those of causality or entropy because it even allows us to predict the
Rankine-Hugoniot conditions as well as selecting a unique limiting solution as the
viscosity tends to zero.
2.5.3 Other discontinuities
A much more general discussion of discontinuous solutions of partial differential
equations will be given in Chapter 7. That chapter is rather lengthy, mostly because
of the delicate nature of the subject, and there could be no better example of this
than the modelling of gasdynamic shock waves in the presence of chemical reactions
which are localised near the discontinuity, which is then often called a detonation.
In this case, the right-hand side of (2.4) is replaced by a localised source term,
which means that the Ranldne-Hugoniot relation for the energy changes from
(2.49) to
L
7P
+1(V-u)2l+=E,
('Y-1)P 2 J-
where E is the prescribed constant energy per unit mass released during the reac-
tion. When E is zero, we can, as mentioned above, derive non-unique weak solu-
tions in which [p)+-, [p]± and [uJ+ satisfy the Rankine-Hugoniot relations (2.49).
It can be shown that we can rearrange these relations into
ry + 1 - (ry - 1)/p
P=
(7 +
1)/3 - (7 _ 1)'
where p and p are the ratios of the downstream to the upstream pressures and
densities, respectively (upstream referring to gas that has not yet traversed the
discontinuity). Thus (p, 1/p) lies on a hyperbola called the Chapman-Jouguet
(C-J) curve, as shown in Fig. 2.16(a), with the point (1,1) corresponding to the
upstream condition. The unique causal weak solution corresponds to p > 1, 1/0 <
1, which is why the lower half of the C-J curve is shown dotted. All points on the
upper half represent admissible shocks.
However, when E is positive the denominator in the p, p relation is increased
by a positive multiple of E and the new C-J curve is shown relative to the old
one in Fig. 2.16(b); the point (1, 1) still represents the upstream condition. The
middle section of this curve is shown broken and is irrelevant, because it is easy
to see from the other Rankine-Hugoniot relations that, when p > 1 and 1/p > 1,
the velocity of the gas traversing the discontinuity is in the wrong direction, from
downstream to upstream. What is most important, however, is that when E > 0
we can no longer resort to entropy or causality arguments to render points on
the lower half of the C-J curve inadmissible. Compressive detonations certainly
exist, corresponding to the upper continuous branch of the curve in Fig. 2.16(b).
However, expansive `deflagration', corresponding to the lower continuous branch,
can also occur, although they are more prone to instability, as people who run
explosives laboratories know well.

SYSTEMS WITH MORE THAN TWO INDEPENDENT VARIABLES 63
C-lo
Ii
I/P
1
1/0
Fig. 2.16 The Chapman-Jouguet curve (a) without energy release, E = 0, and (b) with
energy release, E > 0.
*2.6 Systems with more than two independent variables
It would be nice to be able to end the chapter in the' same way as we did in
Chapter 1 by saying that the ideas developed thus far can be extended trivially to
systems with more than two independent variables. Unfortunately, apart from the
Cauchy-Kowalevski theorem, this is so far from being the case that readers with a
nervous disposition should perhaps refrain from scanning the following pages and
skip directly to Chapter 3.
When we attempt to generalise the ideas of characteristics to equations with
more than two independent variables, we immediately run into difficulties with
geometric visualisation. This is because, if we consider the general m x n system
A,Lu =c, u=(u,) for1<j<, n, (2.51)
=1
we have to seek the solution to the Cauchy problem by considering initial data for
which u is given on a manifold of dimension m - 1. Now if we ask what (m - 1)-
dimensional manifolds are such that the partial derivatives of u normal to the
manifold are not well defined, it is easiest to proceed by denoting such a manifold
by, say,
0(x1,... ,x,,,) = 01
and hence regard the manifold as a level set of a family of functions ¢ that are
smooth enough that we can change to 0 as a new independent variable. Then
(2.51) simply tells us that
Ai
(m8)O
u (2.52)
8x; Fo
is equal to a linear combination of c and the derivatives of u tangential to the
surface
= 0, and is therefore known in terms of the Cauchy data. Hence, if we
define
64
FIRST-ORDER QUASILINEAR SYSTEMS
a0
00
= det
Aj-q0--)
Q axt ..., axm
ox;
we are led to define a characteristic surface 4' = 0 as one on which
0.0
ail
Q
axt
, ... , axm) = 0.
(2.53)
This clearly reduces to the first two of (1.7) and (2.26) when m = 2 and n = 1,
2, respectively. Equation (2.53) also reduces to (1.32) in the scalar case, and our
remarks about the interpretation of (1.32) as a partial differential equation apply
equally to (2.53).
In principle, it is easy to generalise the Cauchy-Kowalevski theorem to prove
the existence and uniqueness of solutions to the Cauchy problem when the data
is given on a non-characteristic manifold, given the usual crucial requirements of
locality and analyticity.
On the other hand, when m > 2, not only do we have the irksome task of
solving a partial differential equation for 0, but also it is more difficult to visualise
what (2.53) means for the surface 0 = 0. However, bearing in mind that the
normal to the surface is always (a¢/ax;) = (£;), say, we can see that (2.53), being
a homogeneous expression of degree n in these quantities, states that at any point
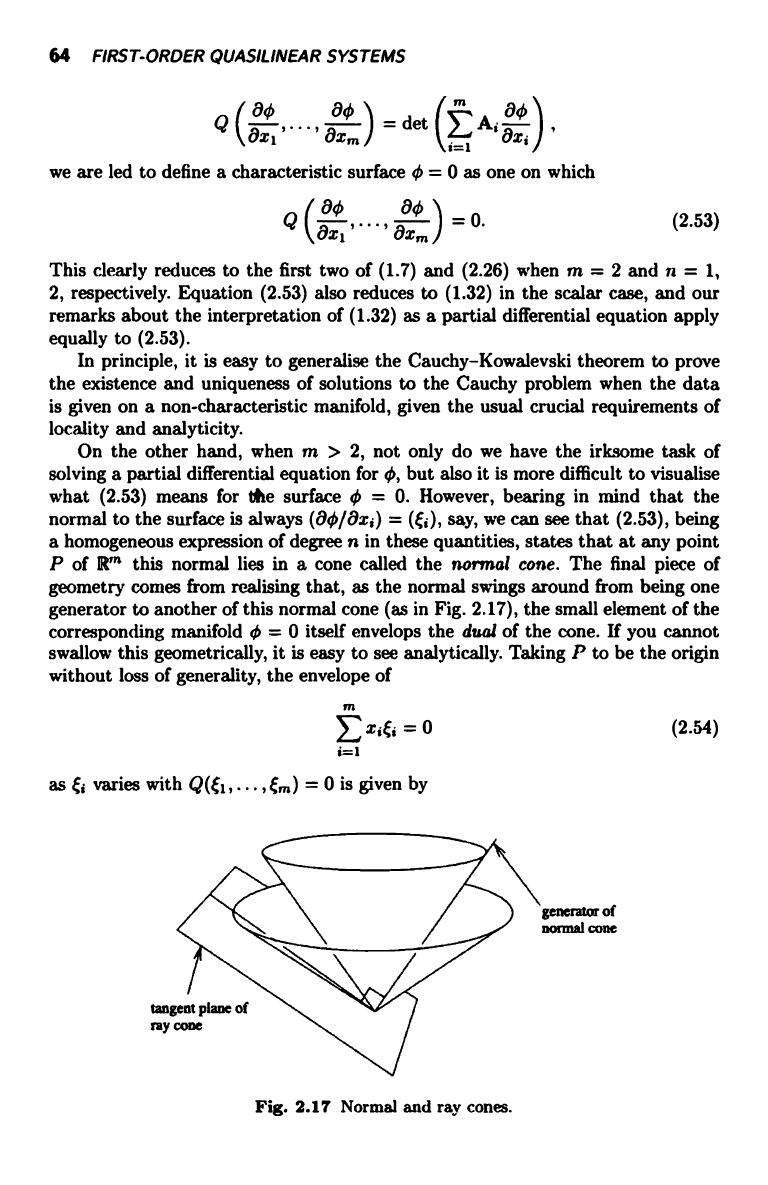
P of R1 this normal lies in a cone called the normal cone. The final piece of
geometry comes from realising that, as the normal swings around from being one
generator to another of this normal cone (as in Fig. 2.17), the small element of the
corresponding manifold 0 = 0 itself envelops the dual of the cone. If you cannot
swallow this geometrically, it is easy to see analytically. Taking P to be the origin
without loss of generality, the envelope of
m
0
;.t
as {; varies with Q(£1i ... , m) = 0 is given by
generator of
normal cone
(2.54)
Fig. 2.17 Normal and ray cones.

SYSTEMS WITH MORE THAN TWO INDEPENDENT VARIABLES 65
(xi&i)
- p = 0
for i = 1, ... , m, (2.55)
i=1
where p is a Lagrange multiplier. Hence we obtain
xi
=,ULQI
Q(61...It.,,) = 0
(2.56)
as the parametric representation of the envelope. It is clearly a homogeneous ex-
pression of degree n, this time in our base coordinates xi, and thus also represents
a cone, called the nzy cone. To visualise the characteristic surface, all we have to
think of is the ray cones dotted around in Rm; a surface is characteristic if it is
tangent to each ray cone at every point. For scalar equations, in which n = 1, the
ray cones all collapse into lines, as in Fig. 1.2.
Once this picture has emerged, the concept of hyperbolicity takes on an entirely
new flavour, because we no longer have a slope A whose reality or otherwise could
be used as a criterion. Instead, we are motivated to consider the possible geometry
of the normal and ray cones and ask how degenerate they are. For example, if
Q(ti,... ,
is positive definite, the null vector is the only generator of the normal
cone. We hope it is clear that the cones that have the greatest `structure' are those
for which there are n sheets all separated from each other; of course, some of these
sheets might be flat (hyperplanes) or lines (one-dimensional).
The surprising result, which can only be verified by obtaining certain integral
estimates on the bounds for u, is that the Cauchy problem for the system (2.51)
only turns out to be well posed in the sense defined after (2.24) when the normal
and ray cones have the maximum structure they could have. To be precise, the
Cauchy data must be prescribed on what is called a space-like hypersurface. Such
hypersurfaces only exist if the ray cone has the maximal number of sheets that
it could have and, in addition, all the sheets are `nested' inside each other. Then
the space-like hypersurfaces lie outside the `outer' sheet of the ray cone; directions
pointing inside this outer sheet are called time-like vectors.
We can illustrate this idea by combining two gasdynamics models, the unsteady
one-dimensional model (2.3) and (2.4), and the steady two-dimensional model
(2.5)-(2.7) and, as in the example on p.42, linearising about a uniform velocity
(U, 0) to give
Oil 8u
_ _ao 8p
+ U
8v OF)
+
G
ao 8p
8t 8x
po 8x'
8t
8x po 8y'
8p 8p
2
eu 8v
(2.57)
8t +U
8x + pogo 8x
+ 8y
= 0.
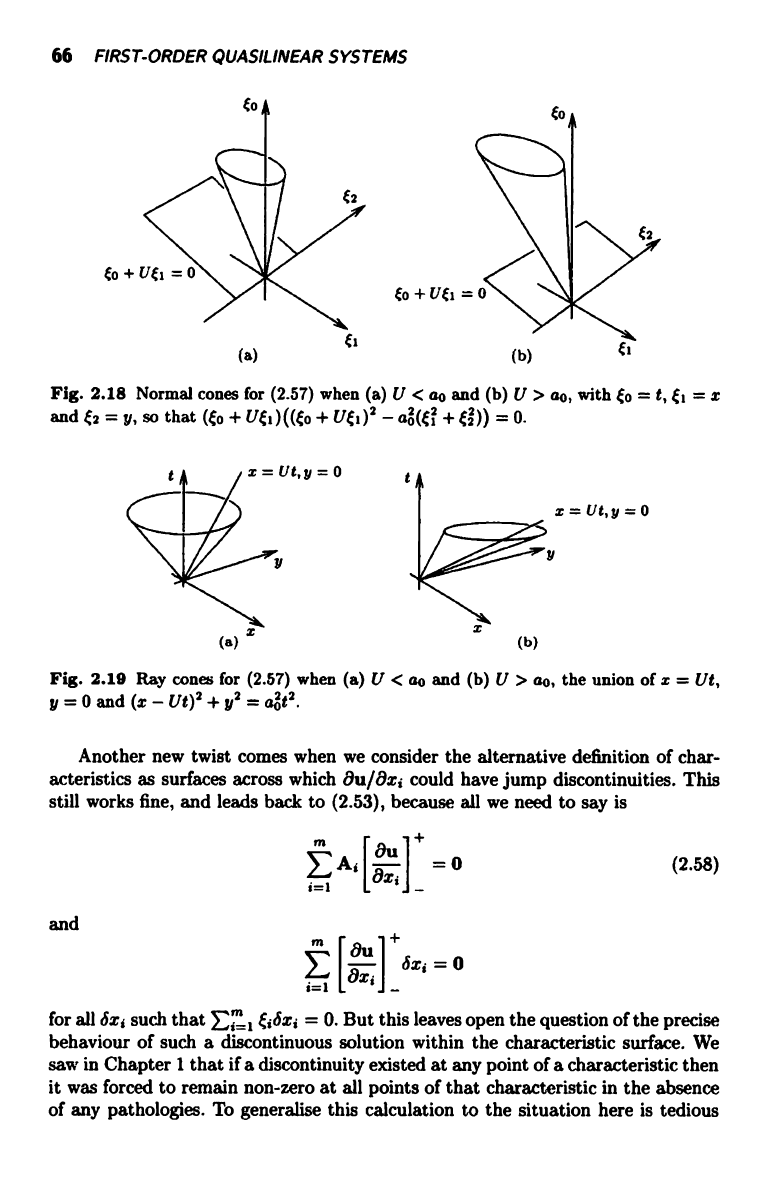
When U > 0, the cones in (x, y, t) space are as in Figs 2.18 and 2.19; the (x, y)
plane is always space-like but, when U > ao, the time axis is no longer time-liken
27The same phenomenon occurs in the theory of relativity, when a particle travels faster than
the speed of light in the material through which it is moving; it emits what is called Zerenkov
radiation.
66
FIRST-ORDER QUASILINEAR SYSTEMS
fo
to+Uti =
(a)
(b)
Fig. 2.18 Normal cones for (2.57) when (a) U < ao and (b) U > ao, with to = t, ti = x
and t2 = y, so that ({o + U{,) (({o + Uti )2 - a2 (E + ai )) = 0.
x=Ut,y=0
Fig. 2.19 Ray cones for (2.57) when (a) U < ao and (b) U > ao, the union of x = Ut,
y = 0 and (x - Ut)2 + y2 = apt2.
Another new twist comes when we consider the alternative definition of char-
acteristics as surfaces across which 8u/8x; could have jump discontinuities. This
still works fine, and leads back to (2.53), because all we need to say is
(2.58)
and
[i9u1+6.T,=0
8x
t=i
for all dxi such that E', {6x{ = 0. But this leaves open the question of the precise
behaviour of such a discontinuous solution within the characteristic surface. We
saw in Chapter 1 that if a discontinuity existed at any point of a characteristic then
it was forced to remain non-zero at all points of that characteristic in the absence
of any pathologies. To generalise this calculation to the situation here is tedious

SYSTEMS WITH MORE THAN TWO INDEPENDENT VARIABLES 67
but, bearing in mind (2.58), we can see that the change of any jump [Ou/8x11
across the characteristic surface in a direction bx tangential to that surface is
x; x; -
J
However, the partial differential equation gives
m
r
2
+
au
ax;ax;
-
j_1
t
dx3.
a
8
terms linear in
Now we can only obtain information about [8u/ax;]± by suitably combining the
second-order derivatives, and this clearly gives that the tangential derivative of
the jump of some linear combination of Ou/8x, is only expressible in terms of that
jump when we take the derivative along the generator of the ray cone tangent to
the surface. This result generalises (1.34) and, with the jargon introduced there,
the curve formed by these generators is called the bicharacteristic. Intuitively, we
can think of bicharacteristics as the only curves in the characteristic manifold that
can transmit information. We give a physical interpretation of this in Chapter 4
and describe how to construct the bicharacteristics in §8.2.6.
Rankine-Hugoniot conditions can be written down for weak solutions of higher-
dimensional equations in conservation form, the simplest system being
8x
v(u) = 0,
(2.59)
where V _ (0/8x2, ... , 010x,,,) and u may be either a scalar or a vector, v being
a vector or (m - 1) x n matrix function of u, respectively; in the latter case, t v
is interpreted as the column vector formed by taking the divergences of the rows
with respect to x2, ... , x,,,. Then (2.45) generalises to
[ U ]
(2.60)
across a shock manifold defined by
xm) = 0.
We conclude with a surprisingly negative remark that can be made about non-
analytic partial differential equations with three or more independent variables.
Recall that, in the Cauchy-Riemann system, we have already displayed an equation
with two independent variables for which there is no solution in the neighbourhood
of a point at which non-analytic Cauchy data was prescribed. Now we can transfer
this result into the statement that the inhomogeneous Cauchy-Riemann equations
au av ,
8v
au
8x-8y=f(x), 8x+8y=0,
02u
+
]
[
(2.61)
with
