Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

48 FIRST-ORDER QUASILINEAR SYSTEMS

ICmnl < ICmnl = Cmn.

However, (2.36) is

8U _ Md 8U

U(6 y) =

May

(2.38)

1 - U/Pd 8y

P-(1 - y/Pa )

which can be solved explicitly as in §1.3 and expanded in the form (2.37). This

gives the convergence of (2.37) and hence, by comparison, the convergence of (2.35)

to the unique analytic solution of the Cauchy problem. Now, of course, the prob-

lem (2.38) does not represent any real simplification over the problem (2.33), and

in any event both can be solved as in Chapter 1. However, the argument above

carries over almost unchanged when (2.33) is a vector equation for u, in which case

it is not solvable by the methods of Chapter 1. In this case (2.38) also becomes a

vector equation for U, but it transpires that all the components of U are equal so

that U can still be found explicitly as the solution of a scalar equation.

Note that the region in which the theorem guarantees existence of the solution

is restricted both by the size of Pa and Pd and by the possibility of blow-up of U;

the latter may impose quite a severe restriction when M. and Md are large, and

this emphasises the local nature of the theorem (see Exercise 2.6).

2.4

Hyperbolicity

We cannot overemphasise the restrictions on D and u that the Cauchy-Kowalev-

ski theorem demands, nor the requirement that the partial differential equation

can be written in the form 8u/8x = D(u) 8u/8y. However, even when all these

restrictions are met, because the theorem uses Taylor series expansions, it only

tells us about local existence and uniqueness and the Cauchy-Riemann system

demonstrates how local the existence result can be.

There are now two ways in which we can try to develop a more global theory for

those partial differential equations whose solutions can be expected to exist away

from any curve on which boundary conditions are posed. We could either look

for solutions of 8u/8t = D(u) Ou/8y which satisfy boundary conditions different

from, and less restrictive than, the Cauchy data (2.32) (for example, we could

prescribe fewer than n components of u on the boundary), or we could ask for

further restrictions on D whereby the Cauchy problem is well posed and hence

has a solution which is not restricted to some very small neighbourhood of the

y axis. We recall that in the first-order scalar equations of Chapter 1 no such

restriction was needed on the coefficient D.

The former approach leads us to the initial and boundary value problems for

elliptic and parabolic equations to be discussed in Chapters 5 and 6. The latter

idea leads to the concept of hyperbolicity and hyperbolic equations, which will be

described in detail in Chapter 4 for scalar second-order equations. However, we are

already in a position to describe an intuitive framework within which to answer

the question as to how D(u) should be restricted for the Cauchy problem for a

first-order system to be well posed.

HYPERBOLICITY 49

2.4.1 Two-by-two systems

We saw in §2.2 that, in certain cases, Riemann invariants exist for a system of

dimension two and hence a certain known function is constant along any charac-

teristic. Suppose now that the partial differential equation A 8u/Bx+B Ou/e9y = c

is in fact such that (2.26) yields two real distinct characteristics C1,2, and that the

consistency condition (2.27) can be integrated for both the Riemann invariants.

This occurs, for example, if A and B are constant and (2.26) has real distinct roots

for y/i. In this fortunate circumstance, if we prescribe u on a boundary r which is

nowhere tangent to C1,2, we can find u(P) by merely solving the pair of simultane-

ous algebraic equations given by the Riemann invariants at P (see Fig. 2.6(a)). We

can then immediately assert that the solution at P exists, is unique and depends

continuously on the data until or unless some pathology develops in the solution

of these algebraic equations. Thus the Cauchy problem is well posed.

In more general cases, we could imagine taking a sequence of points Pi close to

IF and iterating as indicated in Fig. 2.6(b), regarding A and B as constants in each

iteration. Hence, even when equations (2.26) and (2.27) do not have integrals, we

conjecture that, for a quasilinear first-order system of dimension two, the Cauchy

problem is well posed provided that (2.26) has two real distinct roots at each point

(x, y, u) of interest, that is, provided two characteristic directions exist at each

point. This provides the motivation for defining a hyperbolic system of dimension

two as one in which (2.26) has two real distinct roots for y/i. In general, these

roots depend on the solution u; even in the semilinear case when A and B depend

only on x and y, a system may be hyperbolic in only part of a given domain, so

that a problem of mixed type occurs. For the scalar equation aOu/8x+bOu/Oy = c

the problem is necessarily hyperbolic, and for the two-by-two vector case (2.21)

we distinguish the three possibilities, namely elliptic, parabolic and hyperbolic,

depending on whether there are no, one or two real characteristics, respectively.

This observation is the basis of the more detailed discussion of Chapter 3, where

(a)

(b)

Fig. 2.6 Solution by characteristics: (a) A and B constant; (b) approximate solution

when A and B are functions of u.

FIRST-ORDER QUASILINEAR SYSTEMS

we will see that the parabolic case is especially delicate. Indeed, the case where

both A and B are the identity matrix is parabolic under this classification, even

though the system comprises two scalar hyperbolic equations.

2.4.2

Systems of dimension n

With n dependent variables, (2.26) shows that at most n characteristic directions

exist at a point. Guided by a motivational argument similar to that which led to

Fig. 2.6, the system is said to be hyperbolic at that point if (2.26) has n distinct

real roots for A = y/i.

In order to consider the possibility of R.iemann invariants for systems of di-

mension n, we define the left eigenvector I corresponding to a root A

that

IT(B

- AA) = OT.

Premultiplying the partial differential equation by IT, we obtain

ITA 18 +ABn 1 =ITC.

If t is a scalar variable parametrising the characteristic, the generalisation of (2.27)

ITAiu = lT c i. (2.39)

Again, it is just one ordinary differential relation for the variation of a combination

of the n components of u along the characteristic. As remarked earlier, only when

n = 1 is it a first-order ordinary differential equation for u which, in the linear case,

reduces to a quadrature. In general, it cannot be integrated except for constant

coefficient equations, when, along the characteristic,

ITAn = IT 1 c dx'. (2.40)

The unlikelihood of integrating (2.39), even in the case c = 0, can be seen at once

when n = 3, because it is well known that the Pfafan

P du = Pi (u) dul + P2 (u) du3 + P3 (u) du3

is proportional to a total differential dqS(u) if and only if

the curl being taken with respect to u. Thus, even autonomous equations with

c = 0 rarely have Riemann invariants as soon as n >, 3.

If n Riemann invariants do exist for a hyperbolic system, then on each charac-

teristic there is one algebraic relation between the n components of u. The exis-

tence and uniqueness of u are thus assured in some neighbourhood of a boundary

on which u is prescribed, assuming the boundary is nowhere parallel to a char-

acteristic. However, we must be careful with the definition of this neighbourhood

HYPERBOLICITY 51

Fig. 2.7 Domain of dependence of P (shaded).

when n > 2; for example, if boundary data u = uo(s) is only given on a segment

81 < 8 <, 82 of the initial curve, then clearly the domain of existence is restricted

to a region such that all n characteristics at each point P of the region intersect

the given segment of the boundary, as in Fig. 2.7 for the case n = 4.

If P is the intersection on one side of r of the extreme characteristics through

8 = 83 and s = 84, the domain enclosed by the boundary and these extreme

characteristics is called the domain of dependence of P. We have only indicated

this domain on one side of r in Fig. 2.7 because, for most hyperbolic problems

that arise as models of physical phenomena with two independent variables, one

of these variables is 'time-like'; that is, solutions are only required for which this

variable increases away from the `initial' data on the boundary.22 The solution

at P depends on the boundary data given within its domain of dependence and

is independent of boundary data given on sections of the boundary outside it.

Equally, a given point Q on the initial curve has a region of influence defined

by the extreme characteristics through it, as in Fig. 2.8; that is, a change in the

boundary data at Q would change the solution everywhere in its region of influence,

and only there.

The generalisation of Fig. 2.6 to cases where n > 2 suggests that solutions

may be constructed numerically by approximating the characteristic curves by

straight lines and approximating the differential relations (2.39) holding along

characteristics by algebraic relations. Thus Fig. 2.9 shows how the solution at P

may be obtained from a knowledge of u at four different points on the initial curve

in the case n = 4. By varying P, data on a new initial curve is obtained and the

process repeated. This procedure clearly fails if two characteristics become parallel,

in which case the problem ceases to be hyperbolic, or if two characteristics of the

same family intersect, as happened in §1.4 for the case n = 1.

22 We will see in §2.6 that hyperbolic systems with more than two independent variables allow

a much more precise definition to be made of the term time-like.

52 FIRST-ORDER QUASILINEAR SYSTEMS

Fig. 2.8 Region of influence of Q (shaded).

Fig. 2.9 The solution at P using linear approximations to the characteristics.

If Riemann invariants exist, some explicit results may be obtained in closed

form. The following examples (which refer to the models introduced in §2.1) and

remarks illustrate the kind of information that may be obtained.

2.4.3

Examples

Shallow water theory

In this example, described by (2.1) and (2.2), we identify (z, y) in our general

discussion above with (t, z), and we find

A=u±a, where a= &,

and the Riemann invariants are u ± 28, respectively. The system is always hyper-

bolic unless the river is dry, but the nonlinearity means that the characteristics

HYPERBOtICITY 53

can often intersect, corresponding to the formation of a `bore' or `hydraulic jump'.

In §4.8.1 we will see how to use these Riemann invariants to generate some useful

explicit solutions to (2.1) and (2.2).

This example illustrates the point that the existence of Riemann invariants is by

no means a necessary condition for a first-order system to have explicit solutions,

because we cannot usually locate the characteristics explicitly. Among the many

clever `tricks' for guessing explicit solutions, one possibility to keep in mind for

autonomous systems such as (2.1) and (2.2) is that of exchanging the roles of

dependent and independent variables. We see that, if we attempt the hodogrnph

transformation

x = X(u, h),

t = T(u, h), (2.41)

so that, by the chain rule,

1 ax

at -dah'

etc., with the Jacobian

_8T Ox

OT OX

Ou8h ahau

assumed non-zero, then we obtain the linear system23

aT 8T_

ah -

U - 5 7

h + au 0'

8u - u

= 0,

where we have set g = 1 for simplicity. This of course only works because there are

no undifferentiated terms in the original equations (2.1) and (2.2), but it has an

interesting geometrical interpretation which will be discussed further in Chapter 4.

Unsteady one-dimensional gas dynamics

Rearranging (2.4) (with the help of (2.3)) as

Tt OX

and again identifying (t, x) with (x, y), we find, after some calculations (Exer-

cise 2.10), that the system is always hyperbolic with

A=u or

\=u±JJ_T

V P

as the slopes of the characteristics, on which

rypdp - pdp = 0,

ryppdu + dp = 0,

respectively. Hence p/p7 is constant on dx/dt = u but, in general, Riemann in-

variants do not exist on all three families of characteristics.

23See (301 for

a discussion of the corresponding system in gas dynamics.

FIRST-ORDER QUASILINEAR SYSTEMS

Steady two-dimensional gas dynamics

Our analysis in §2.2 of the linearised system (2.8)-(2.10) has already revealed the

existence of three real distinct characteristics when the basic flow is supersonic,

and it is only under these circumstances that the system is hyperbolic. A slightly

different situation arises for the full (unlinearised) system (2.5)-(2.7) where, after

more lengthy algebraic manipulations (Exercise 2.11), we find

A twice or A = tan (tan-' (V)

f sin-'

p(u2 + v2)

Now, there are four real roots when u2 + v2 > ryp/p, in which case the flow is again

said to be supersonic. However, the system is not strictly hyperbolic even when

the flow is supersonic because two of the eigenvalues, namely A = v/u, coincide; in

practice, however, the solutions usually behave as if the system were hyperbolic.

In both of the examples above, neighbouring members of the second or third

families of characteristics found above can intersect in general to form gasdynamic

shock waves. Much more will be said about these shock waves in the next section.

Flow of granular materials

The model (2.13) with h = 1, together with the relation (2.16) between r, o- and

oy, can, after a long calculation (started in Exercise 2.3, where tP is defined, and

continued in Exercise 2.14), be shown to be always hyperbolic with

A=-cot l0±I 4 21

and the Riemann invariants are

fcot0log1-o22av I+2,i

respectively. We remark that these characteristics are not the slip planes that were

needed to formulate the model.

Fluidised and packed beds

The two linear models (2.17) and (2.18), and (2.19) and (2.20) are clearly always

hyperbolic; the characteristics of the latter are given by

= va, vb,

while for the former one of these characteristic `speeds' is zero. However, the pres-

ence of the undifferentiated terms means that there are no explicit Riemann in-

variants unless k or h is zero. Fortunately, the linearity of these models enables us

to circumvent this difficulty, as we shall see in Chapter 4.

As an aside, suppose that k = 0 in (2.19) and (2.20) and we were attempting to

solve the Cauchy problem in which ca and cb, which are now Riemann invariants,

WEAK SOLUTIONS AND SHOCK WAVES 55

were prescribed on the non-characteristic curve t = 0. Now suppose further that

we were interested in modelling a fluidised bed of finite depth, and we were unsure

(as we often are) about the boundary conditions that should be applied at the top

and bottom of the bed. One thing we can be sure of at once is that we should not

impose values of either cQ or cb at the top of the bed, towards which the gas is

moving with velocity va or vb. If such values were prescribed, they would almost

certainly clash with the values of the Riemann invariants that follow from the

Cauchy data.

Optical fibre model

A transformation slightly less obvious than the hodograph transformation (2.41)

can be applied to the optical fibre model (2.11) and (2.12). For a given T, this

system is hyperbolic (unlike most models of slow viscous flow), with characteristics

dx/dt = u, the local fluid velocity, and t = constant, corresponding to infinite

propagation speed in the incompressible glass. However, the presence of T means

that there are no explicit Riemann invariants. Nonetheless, if we write the `partial'

hodograph transformation

x = x(A, t),

u = u(A, t),

and rescale this so that r = fo T(t') dt', we find (Exercise 2.15) that x satisfies the

linear equation

82x 82x

1 ex

8A2 - c8A8r q 8A'

which can be solved explicitly for 8x/8A. This enables us to show that the char-

acteristics never intersect.

The whole question of finding whether any given quasilinear system has enough

symmetry to be able to be integrated explicitly is intimately connected with the

theory of groups that depend on a continuously-varying parameter. We will return

to this on several later occasions but, for now, the all-too-frequent occurrence of

shock waves as a result of the intersection of characteristics of hyperbolic systems

demands immediate attention.

«2.5

Weak solutions and shock waves

We have shown at the end of §2.2 that, for a hyperbolic system, the first derivatives

of u can be discontinuous across a characteristic, and in Chapter 1 we have given

several examples where characteristics may intersect to cause discontinuities in u

itself. Hence, following the discussion of weak solutions for the scalar equations of

Chapter 1, we examine the possibility of jump discontinuities in u across a curve r

for the system A 8u/8x + B Ou/ey = c. Because Green's theorem plays a crucial

role, we only really have any hope of generalising the theory presented in §1.7 for a

hyperbolic system when it is in conservation form. Hence we consider the problem

of defining a weak solution of

8u 8v

+ 8y

= C,

(2.42)

FIRST-ORDER QUASILINEAR SYSTEMS

where v and c are functions of u, x and y; for simplicity, initial data u = uo(y) is

given on x = 0 and the domain of interest is x > 0. For (2.42) to be hyperbolic, the

matrix (Ov;/Suj) must have n distinct real eigenvalues. If we now multiply (2.42)

by a test function O(x, y), differentiable everywhere in x > 0 and such that

-+ 0

sufficiently rapidly as x or y -+ oo, then, using Green's theorem on the half plane

x > 0, we obtain

+ v

+ 1 c I dx dy

(2.43)

I u

>o \

8x ey ey

The statement (2.43) generalises (1.25), and our restrictions on the behaviour

of 0 have left us with a convenient right-hand side. The equation makes sense

even if u is discontinuous, and hence we define a weak solution of (2.42) to be a

function u satisfying (2.43) for all suitable test functions v/0. If the weak solution u

is continuous then clearly, retracing our steps, (2.43) implies (2.42) and a classical

solution is a weak solution. A weak solution need not, however, be continuous; if

it is discontinuous across a curve F then, carrying over the argument leading to

(1.27) and applying Green's theorem to (2.43) for the domain x > 0 excluding r,

we obtain

Ir [tGu]± dy = J [ 1'v]± dx. (2.44)

Since zji is continuous across r and (2.44) holds for all such ip, then, necessarily,

= [v]+,

(2.45)

(u)±

which is the jump or Rankine-Hugoniot condition for a general hyperbolic system

of conservation laws.

For a semilinear problem, v is equal to Du, where D is a matrix which does not

depend on u, and hence dy/dx is an eigenvalue of D. In this case discontinuities

in u can occur across any of the characteristics. In general, however, they lie on

curves called shocks, which are definitely not characteristics.

Of course, the approach above inherits all the non-uniqueness properties that

were encountered in Chapter 1 for the case n = 1. We will now describe two ways

in which this non-uniqueness might be resolved.

2.5.1 Causality

We begin by remarking that we can construct weak solutions by piecing together

classical solutions using the jump condition (2.45). At a point P on the shock there

are n characteristic directions on each side of it, as in Fig. 2.10 for the case n = 2.

These 2n characteristics through P form two classes, those that intersect x = 0

and those that do not.

On each characteristic which intersects x = 0, some information propagates

about the boundary data uo(y); in the special case when a Riemann invariant

exists on the characteristics, this takes the form of a prescribed algebraic relation

between the components of u as we approach the shock (from the left in Fig. 2.10).

For the shock strength (u) and direction to be defined uniquely it is necessary that

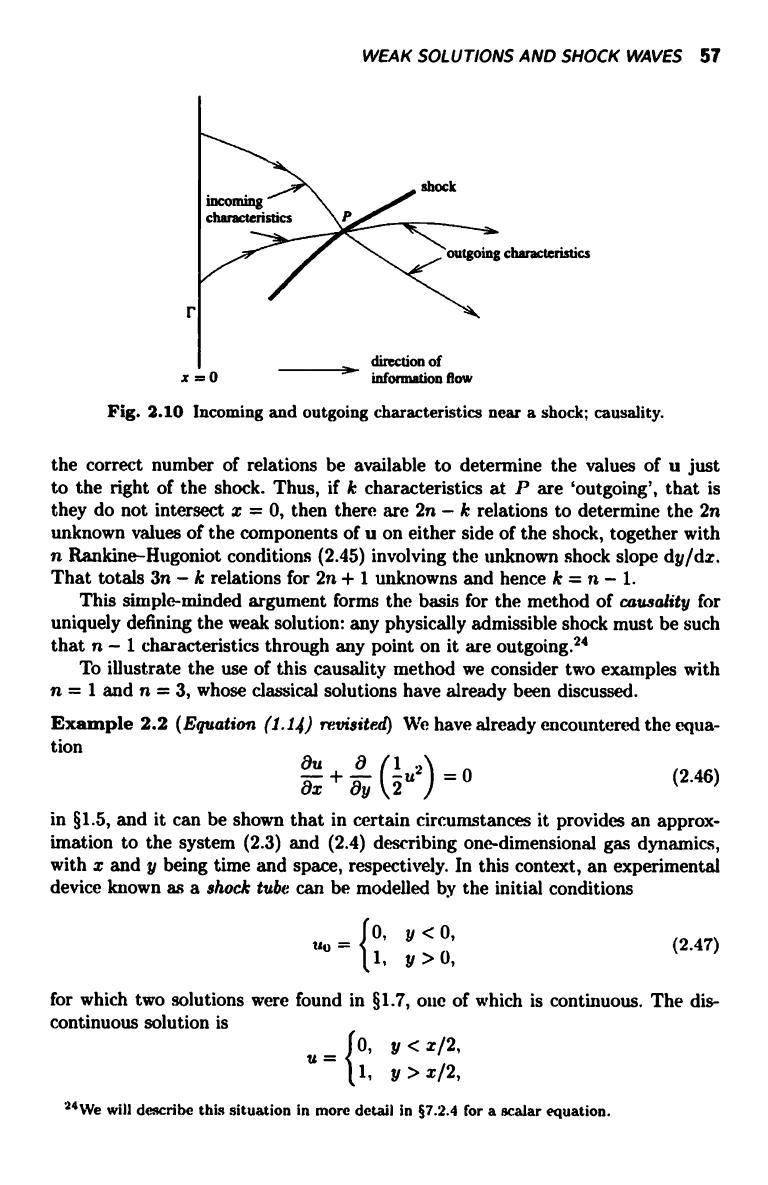
WEAK SOLUTIONS AND SHOCK WAVES 57

Fig. 2.10 Incoming and outgoing characteristics near a shock; causality.

the correct number of relations be available to determine the values of u just

to the right of the shock. Thus, if k characteristics at P are `outgoing', that is

they do not intersect x = 0, then there are 2n - k relations to determine the 2n

unknown values of the components of u on either side of the shock, together with

n Rankine-Hugoniot conditions (2.45) involving the unknown shock slope dy/dx.

That totals 3n - k relations for 2n + 1 unknowns and hence k = n - I.

This simple-minded argument forms the basis for the method of causality for

uniquely defining the weak solution: any physically admissible shock must be such

that n - 1 characteristics through any point on it are outgoing.24

To illustrate the use of this causality method we consider two examples with

n = 1 and n = 3, whose classical solutions have already been discussed.

Example 2.2 (Equation (1.14) revisited) We have already encountered the equa-

tion

+ 8y ( 2

u2)

= 0

(2.46)

in §1.5, and it can be shown that in certain circumstances it provides an approx-

imation to the system (2.3) and (2.4) describing one-dimensional gas dynamics,

with x and y being time and space, respectively. In this context, an experimental

device known as a shock tube can be modelled by the initial conditions

_ Jo y < o

Y>01

(2.47)

for which two solutions were found in §1.7, one of which is continuous. The dis-

continuous solution is

y < x/2,

1, y>x/2,

24We will describe this situation in more detail in §7.2.4 for a scalar equation.