Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

(a)

(b)

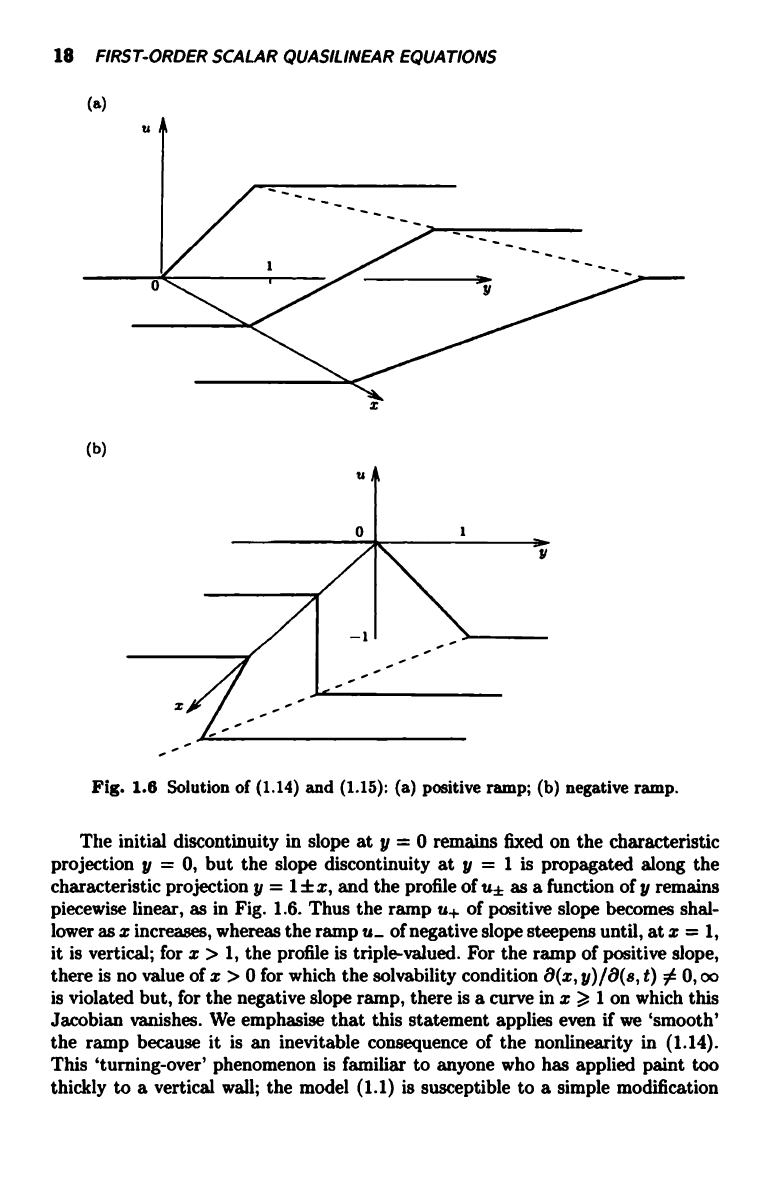
Fig. 1.6 Solution of (1.14) and (1.15): (a) positive ramp; (b) negative ramp.

The initial discontinuity in slope at y = 0 remains fixed on the characteristic

projection y = 0, but the slope discontinuity at y = 1 is propagated along the

characteristic projection y = 1±x, and the profile of of as a function of y remains

piecewise linear, as in Fig. 1.6. Thus the ramp u+ of positive slope becomes shal-

lower as x increases, whereas the ramp u_ of negative slope steepens until, at x = 1,

it is vertical; for x > 1, the profile is triple-valued. For the ramp of positive slope,

there is no value of z > 0 for which the solvability condition 8(x, y)/8(8, t) 0 0, 00

is violated but, for the negative slope ramp, there is a curve in x > I on which this

Jacobian vanishes. We emphasise that this statement applies even if we `smooth'

the ramp because it is an inevitable consequence of the nonlinearity in (1.14).

This 'turning-over' phenomenon is familiar to anyone who has applied paint too

thickly to a vertical wall; the model (1.1) is susceptible to a simple modification

SOLUTIONS WITH DISCONTINUITIES 19

of the analysis just given. The same remark applies to traffic pile-ups, or other

situations described by the kinematic waves that we mentioned at the beginning

of the chapter. However, on the mathematical side, the phenomenon has serious

implications for the whole study of nonlinear partial differential equations because

these kinds of discontinuities are likely to be encountered whenever we try to use

nonlinear equations as mathematical models.

Before we consider what to do about this, let us also note that there is another

aspect to partial differential equation models involving discontinuities. This is the

observation that many physical phenomena that we would like to model can only

be represented at all conveniently by differential equations, possibly even linear

ones, whose solutions have discontinuities across boundaries which themselves have

to be determined as a part of the solution. Such configurations are called Jnee

boundary problems and we will devote a chapter to them later on. For the moment

we note that they could occur when modelling heat flow in a material that can

change phase or otherwise react chemically in a very thin layer, such as a flame; in

either case there is a discontinuity in the heat flux at the free boundary. Equally,

a free surface between two immiscible fluids can be considered as a discontinuity

in density, or a tumour growth boundary as a discontinuity in the concentration

of some biological agent. The only difference in principle between these examples

and (1.14) is that, in the latter case, the discontinuity occurs spontaneously as

x increases, while the above-mentioned physical examples have their singularity

imposed in the prescription of the problem.

This state of affairs motivates us to consider a more imaginative approach to

partial differential equations than that of prosaically searching for what we have

called classical solutions, in which the dependent variable and its derivatives are

all smooth enough to satisfy the differential equation everywhere. We could be

ambitious, and allow solutions to be singular at points (which could be relevant

to, say, models for explosions) or on tines (to model, say, vortices in fluids or

superconductors), but here we will only consider discontinuities across surfaces of

one dimension fewer than the dimension of the space of independent variables (i.e.

curves, as far as most of this chapter is concerned).

1.6

Solutions with discontinuities

Our first naive idea based on (1.14) (and its yet-to-be-revealed relevance to, say,

shock waves in gas dynamics) is to contemplate the idea of a `weak', as distinct

from `classical', solution as a combination of classical solutions, each defined on a

different domain. These domains are then going to be patched together in such a

way that, across the boundaries between domains on which there are discontinuities

in some derivatives, a suitably generalised form of the governing equation (1.2),

Ou Ou

aOx

+ 68y = c,

is satisfied. The definition will be made precise, even when u itself is discontinuous,

in the next section, but let us consider first the problem of looking for a solution

for which only the first derivatives of u may be discontinuous across some curve

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

C in the (x, y) plane, while u itself is continuous there. If the curve is defined by

x = x(t), y = y(t) and we denote the limiting values of functions as this curve is

approached from either side by superscripts + and -, then

+ 8u+ 8u+ 8u

u =x8x +y8y

tC=x8x +yay

Since u is continuous across C, so1is u, and therefore

x0++y[tul+_=0,

(1.16)

where the square bracket notation denotes the `jump' or finite discontinuity in

the expression across C. The function u must also satisfy the partial differential

equation except on C, so by subtraction we have

a [fix]

+ b

[1i

= 0,

(1.17)

where a and b are evaluated on C without ambiguity since u is continuous there.

The necessary condition for these gradient discontinuities to be non-zero is bi = ay,

and therefore C must be a characteristic projection.

Thus a further interpretation of characteristics is that they are lines on the

solution surface across which there need not be a continuously turning tangent

plane, but instead there is a `kink' or an `edge'? Such a solution is generated

when the boundary curve only has a piecewise continuous tangent vector; it is not

strictly speaking a classical solution since the partial differential equation is not

satisfied on C. However, C does separate regions in which classical solutions can

be defined and calculated without having to consider the size of the discontinuity.

In the linear case, with c(x, y, u) = a(x, y)u + 6(x, y), we can compute the

magnitude of the discontinuity as it propagates along C as follows. First observe

that, if i= aandy=b,

[fix]±-a[8 2] ++b[x8y]+.

Differentiating the original partial differential equation with respect to x and sub-

tracting values on either side of C, we obtain

102uD

[ 82u 1++ 8a [8u1++ fib

loul+ _ a [8u1+

8x2 8x8y J _

fix

fix J

fix

8y fix

Hence from (1.17), and assuming b 0 0,

18)

dt fix _

b fix

fix

so that [8u/Ox]+ never vanishes if it is non-zero at t = 0.

7lndeed, this interpretation motivates an alternative starting point for our definition of char-

acteristics which, unlike that in §1.3, can be generalised to vector partial differential equations,

as we will see in Chapter 2.

(a_La +afib)[8u1+d [8u] +

SOLUTIONS WITH DISCONTINUITIES 21

Motivated by the discussion in §1.5, we now consider a situation in which u

itself may be discontinuous. The dangers inherent in doing this can be illustrated

by looking at a class of problems of which the following is a simple example.

Consider the Cauchy problem

Ou Ou

{o,

y < 0,

u(O,y)=1,

y>0,

and let us enquire whether there is any special curve y = f (x), f (0) = 0, such that

the solution is

y < f(x),

1, y >f(x).

(1.19)

We can give a plausible answer even to the corresponding question for the general

semilinear case, in which the boundary data has a discontinuity in u at the point

s = so, where Si < so < 82. We know that there is a unique classical solution in

the domain bounded by the projections of the characteristics through the points

defined by sl and so - 0, and a further classical solution in the domain bounded

by the characteristic projections through so + 0 and sy. In the semilinear case

the characteristic projection is determined independently of the value of u, so

that a unique characteristic projection Co through s = so is defined (Fig. 1.7).

Thus a classical solution is defined in the two domains D± which are adjacent and

separated by Co. Hence one way of defining a generalised solution in a unique way

is to permit u to have a jump, or finite discontinuity, only across a characteristic

projection such as Co. This implies that f (x) = x in (1.19).

The size of the discontinuity in u is given by the limiting values of u on either

side of Co, which have to satisfy the characteristic equations (1.7), so that

dt [u]± _ (c)± .

Fig. 1.7 Discontinuous boundary data for a semilinear equation.

22 FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

If c is independent of u, the discontinuity in u remains constant; if c = a(x, y)u,

then, on CO,

[u]± = A exp

c a (x(r), y(r)) dr,

where A is constant.

However, in the quasilinear case the limiting characteristic projections Co and

Co are in general different since they depend on the values uo and uo , respectively.

Thus the two domains in which the classical solutions are defined may overlap or

not be adjacent, leading to multi-valuedness or non-existence, respectively. In this

case the existence of a discontinuity in the boundary data alters the solution over

a region larger than just the one characteristic. A new approach is needed, and it

will be described in the next section.

Before we proceed, we emphasise that we cannot be too careful in constructing

any theory of discontinuous solutions of partial differential equations. The moment

we allow the solution to be ill-behaved in any way that is not natural for the

equation, we may be like a fisherman who has cast his net so widely as to catch

every fish in the river. If this happens to us, we must be prepared to have to

filter out many candidate solutions which should not have been allowed in the first

place.

*1.7 Weak solutions

On a curve Co across which u or its first derivatives have discontinuities, the par-

tial differential equation a 0u/& + b 8u/8y = c has no meaning. However, we

have seen in the previous section that jumps, i.e. finite discontinuities, in the first

derivatives of u can be described by piecing together different classical solutions

across characteristics systematically and naturally. The motivation for this section

is to find a similarly systematic way of describing finite discontinuities in u itself.

Such discontinuities are often called shocks, a term originating from partial dif-

ferential equation models in gas dynamics. When shocks are present, the problem

is underdetermined when stated just as a partial differential equation; either a

condition on the value of the discontinuity must be given, or the problem must be

rewritten in such a way that it is meaningful even in the presence of shocks.

For ease of exposition we begin by illustrating the latter procedure for the

linear equation

a(x,y)8x

+ b(x,y)

= a(x,y)u.

(1.20)

We introduce an arbitrary differentiable function 1P(x, y), called a test function, so

that if u is differentiable and satisfies (1.20) then, for all z/i,

ax (,b) + 8y (ln'u)

(-(at) + b (bpi) + ad I

. (1.21)

Thus, if u is prescribed on some initial arc I' and we integrate over a region

D between r and an arbitrary curve y, and +ii is restricted to vanish on y (see

Fig. 1.8(a)), then (1.21) allows us to use Green's theorem to obtain

WEAK SOLUTIONS 23

(a)

(b)

Fig. 1.8 Regions of integration for weak solutions: (a) continuous solutions; (b) discon-

tinuous solutions.

jW(adv - b dx) .

IJn

((a)

+ (biIi) +

dx dy.

(1.22)

Now (1.22) is an identity which can make sense even when u is not differen-

tiable. Hence we define a weak solution of (1.20), with boundary data given on I',

as a function u satisfying (1.22) for all test functions' 0. The key point here is

that this definition does not require u to possess derivatives at all points, only that

the integrals exist; the onus of differentiability has been transferred from u to 0.

If, however, u is differentiable everywhere in a subdomain Do, then, by choosing

suitable test functions and reversing the steps in the argument above, it is easily

shown that u satisfies (1.20) everywhere in Do. A similar remark applies if u has

discontinuous derivatives across a characteristic. However, if u itself is discontin-

uous across an open curve Co, as in Fig. 1.8(b), then the application of Green's

theorem to regions D+ and D- separated by Co gives, after subtraction,

ip[u]±(ady-bdx)=0.

(1.23)

fc.

Since [u]± 96 0 and vP is arbitrary, dy/dx = b/a and Co is a characteristic projec-

tion.

For quasilinear problems this procedure can only be used if the equation is

such that its principal part, i.e. the terms involving the highest derivatives, is in

divergence form OP/ax + OQ/8y, so that Green's theorem can be applied. In this

case,

8P OQ

8x+8y=c,

(1.24)

'In some cases, such as models for gas dynamics, this definition can be motivated physically;

see [301.

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

where P, Q and c are differentiable functions of x, y and u, and the equation is

called an inhomogeneous conservation law (or, when c = 0, simply a conservation

law).

The appropriatee weak solution is then defined to be a function u such that

fJ I PBx +Q y2 +ctj)

dxdy = j1(Pdy - Qdx)

(1.25)

for all admissible test functions i,i, and it is again easily verified that if u is differ-

entiable it must satisfy (1.24). As in (1.23), if u is discontinuous across Co,

([P]±

dy - [Q]± dx) = 0,

(1.26)

and, as 0 is arbitrary, this implies that the slope of the shock at Co is given by

the Rankine-Hugoniot condition9

[Q]{

1 27

dx [P]±'

(

)

This is no longer a characteristic projection in general, but as [u]± -> 0 it tends

to the characteristic projection defined by dy/dx = (8Q/8u)/(8P/8u).10

Example 1.4 Solve the following ((1.14) again):

8U au

8x +u8y =

u(O,y) = f(y)

By a simple generalisation of the discussion following (1.15), this problem fails to

have a classical solution for all x > 0 whenever there are values of y for which

f'(y) < 0. It does, however, have a weak solution defined by (1.25) with P = u,

Q = lug and c = 0. Then the possible curves Co separating domains in which

classical solutions exist have slope such that

dy [12

u2]_

u++u-

[u]+

Now comes the catch alluded to on p. 22: different weak solutions may arise from

the same classical problem. Thus, in this example, if the partial differential equa-

tion were multiplied by u, so that P = xu2 and Q = sus, the definition of the

weak solution would be different and would lead to curves Co with slopes such

that

dy [3u3]

u++u-

dx [1u2]+ #

sThis condition can also be derived from a simple `box' argument in which the jump in density

across a small box centred on the shock is balanced by the jump in flux, much as in the derivation

of mass conservation in §1.1. However, this argument is less easy to apply when there are more

dependent variables.

'°Note that the curve on which the solution of (1.11) is singular is not a characteristic either,

but it has a slope which tends to that of a characteristic as x - oo.

MORE INDEPENDENT VARIABLES 25

Thus, in generalising the classical definition of a solution to the Cauchy prob-

lem, which leads to non-existence when shocks occur, we have lost uniqueness;

additional conditions are needed to retrieve this property. We can see this more

explicitly by returning to (1.14) with the initial data

0, y < 0,

u(O,y) _

11,

y>0.

A solution for which u is continuous but its derivatives are not is

0, y < 0,

y/Z, 0 < y < x,

11,

x<y;

the discontinuities propagate on the characteristic projections y = 0 and y = x.

Thus it is a weak solution. However, another weak solution is

0, y < x/2,

5l 1, y>z/2,

since it satisfies the shock condition (1.27) on y = x/2. Thus there is more than

one weak solution to this Cauchy problem, and in fact many such discontinuous

weak solutions can be constructed. The fears expressed on p. 22 have been realised

and some constraint or `filter' is needed to restore uniqueness. There are several

possibilities, three of which will be discussed at the end of Chapter 2.

* 1.8 More independent variables

We conclude with some brief comments about the extension of the ideas of this

chapter to scalar first-order quasilinear equations with more than two independent

variables, which arise in several applications. For example, when a thin layer of a

viscous liquid flows over a given curved surface z = F(x, y), where z is vertically

upwards, the appropriate generalisation of (1.1) is

8t -

3cA (8x

(Ah"

)

+ -

4h3

ax/,,

= 0'

(1.28)

here A = (1 + (8F/8x)2 + (8F/8y)2)-1/2, c is as in (1.1), and the thickness of

the fluid layer measured normal to the substrate, h, is now a function of x, y and

The general equation has the form

m l9it

E a.,

8x =

for m > 2,

(1.29)

e=1

where ai and c are functions of x; and u. The appropriate generalisation of the

Cauchy data (1.3) is to prescribe u on a surface of dimension m -1 and, to do this,

26 FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

a change of style is appropriate compared to that used in § 1.3. With m coordinates

to deal with, it is worth paying the price of representing the surface as a level set

of a function, say ¢(x1,

. . . ,

xm) = 0, rather than selecting one preferred variable

xm as a function of the others.

We know u on the surface 0 = 0, which determines the m -1 tangential deriva-

tives; together with the partial differential equation, this is in general sufficient to

determine all the first derivatives 8u/8xi on 0 = 0. To see whether this works

analytically, we change from (xi) to new variables (0, tpi), i = 1, ... , m - 1, where

Oi are functions which are independent of 0. Then, by the chain rule,

Ea'8xi

8(b+a Du=c,

where

m-1 m

8x;

(a; 0

1=1 i=1

Hence Ou/84, the derivative of u normal to 0 = 0, can be found as long as

ai-#0.

i=1

8xi

(1.30)

(1.31)

Following (1.5), we say that 0 = 0, which is a surface of dimension m - 1, is a

characteristic surface of (1.29) if

8d'

= 0.

(1.32)

i=1 8x;

We now have what seems to be a partial differential equation for ¢, although we

will not need to solve it as such." In fact, since (1.32) only holds on 0 = 0, it is

effectively an (m - 1)-variable partial differential equation, albeit a nonlinear one

(see Exercise 1.16).

It is easy to see that this approach to characteristics coincides with the defini-

tion that a surface is only characteristic if it can sustain a jump in 8u/8xi across

it. Indeed, subtracting (1.30) on either side of ¢ = 0 gives

8&u

o=0+

(ai±.)

8xi

[eel

m=o-

However, the way in which such discontinuities propagate in 0 = 0 is a non-trivial

generalisation of the corresponding result when m = 2, namely that a disconti-

nuity at one point in the Cauchy data simply propagates along the characteristic

projection through that point. First, assume for simplicity that the a; are constant

11 In Chapter 8 we will see that the solution of equations such as (1.32) can always be reduced

to the solution of some ordinary differential equations.

MORE INDEPENDENT VARIABLES 27

and c = 0. This means that the characteristics are hyperplanes and so we can take

0 to be a linear combination of the xi. Then, differentiating (1.30) with respect to

0 and subtracting on either side of 0 = 0, we obtain

ad!

0=0+

ai-

I +(a.V)

00 1

0. (1.33)

_0_

m=u-

Hence, on a characteristic 0 = 0,

=0.

I 8"Oul

m=o+

Even when ai and c depend on x; and u, it is easy to see that the right-hand

side of (1.33) is replaced by a term that is simply proportional to (i3u/801

o+,

as in (1.18). Thus we have the interesting result that the coefficients ai define

a direction in the characteristic surface, called the bicharacteristic direction, in

which discontinuities propagate. Any jump in the Cauchy data at one point of the

initial surface only propagates along the one-dimensional bicharacteristic through

that point. Moreover, it is easy to see that the (m - 1)-dimensional characteris-

tic surfaces are each made up of an (m - 2)-parameter family of bicharacteristic

curves (see Fig. 1.9 for the case m = 3). Of course, bicharacteristics are simply

characteristics when m = 2; for m > 2, they can be used to construct the solution

parametrically by solving the bicharacteristic equations

dtt

; with dt = c,

together with the Cauchy data

u=Uo(S),

x,=x;0(s), s=(si,...,Sm_i).

(1.34)

Fig. 1.9 Characteristic surface and bicharacteristic curve for (1.29).