Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

1.2

Cauchy data

Motivated by these examples and, obviously, by the principle that it is always best

to start from the simplest situation, we now develop a theory for general first-order

quasilinear equations. These are defined to be equations of the form

a(x, y, u) 8 + b(x, y, u) 8u = c(x, y, u), (1.2)

where it is important that a, b and c do not depend on the derivatives of u; we

also assume that a, b and c are smooth (i.e. continuously differentiable) functions

of their arguments.

Suppose that r is a curve in the (x, y) plane; we define Cauchy data to be the

prescription of u on r. It is convenient to write this boundary condition in the

parametric form

x = xo(s), y = yo(s),

u = uo(s)

for al <, s <, 82.

(1.3)

Here xo, yo and uo are smooth2 functions of s such that there is no value of a for

which xo(a) = yo(s) = 0, the prime denoting differentiation with respect to s.

The boundary value problem of finding a continuously differentiable function u

satisfying (1.2) and (1.3) may be interpreted geometrically as that of constructing

a surface u = u(x, y), in the space (x, y, u), called the integral or solution surface,

which satisfies (1.2) and passes through the boundary curve defined by (1.3). This

is an obvious extension of the initial value problem for an ordinary differential

equation, which requires the construction of a curve (i.e. a graph) passing through a

boundary point. For an ordinary differential equation, say a(x, u) 8u/8x = c(x, u),

this is generally possible unless a = 0 at the boundary point, and for the partial

differential equation a subset of boundary curves is unacceptable for a similar

reason.

If we differentiate the boundary data with respect to s along the boundary

curve, then we find

, 8u , 8u ,

uo =

8x xo

+ 8y yo.

(1.4)

Equations (1.4) and (1.2) evaluated on r, where a, b and c are known functions of

s, are two simultaneous equations for 8u/8x and 8u/8y on r. Hence 8u/8x and

8u/8y are determined uniquely on r, provided that the determinant of coefficients

ayo_bxoS0 foralls1 <, s<, 32-

X10 A

If this condition is satisfied and if a, b, c and the Cauchy data have Taylor series

at each point, it can easily be verified that the partial derivatives of u of all orders

are defined uniquely by the Cauchy data and the partial differential equation,

and a Taylor series expansion for u(x, y) about a point on I' can be constructed

2When xo, yo or uo, or a, b, c are not smooth the problem needs a completely new approach,

as we shall see in §1.6.

CHARACTERISTICS 9

formally. This forms the starting point for the Cauchy-Kowalevski existence and

uniqueness theorem, which considers the convergence of this Taylor series and

guarantees a unique solution if condition (1.5) is satisfied; it will be discussed

further in Chapter 2.

If condition (1.5) is not satisfied at a point s = so (or for a range of values of

a) then, in general, no solution exists in the neighbourhood of the boundary curve.

However, in the special case when

xo__1/'o__tb

a b c'

(1.2) and (1.4) are linearly dependent and 8u/8x and Ou/Oy exist but are not

uniquely determined at s = so. In this case many solution surfaces may pass

through a single boundary curve, and this suggests that curves satisfying these

ordinary differential equations have an important role to play, as we shall see in

the next section.

1.3

Characteristics

The partial differential equation (1.2),

a-+ba =c,

has a geometrical interpretation which is also the key to its solution given Cauchy

boundary data x = xo(s), y = yo(s) and u = uo(s) satisfying (1.5). The normal

to the solution surface in (x, y, u) space is (8u/8x, 8u/8y, -1), and we can rewrite

the partial differential equation in the form

(a,b,c)

(_i)

8z8y=0.

Thus, (a, b, c) lies in the tangent plane to the solution surface at each point. Hence,

if we construct a curve (x(t), y(t), u(t)), parametrised by t, by solving the ordinary

differential equations

x = d

= a(x, y,

u),

b =

= b(x, y, u),

u_dt

= c(z,y,u),

then this curve lies in a solution surface for all t. If, in addition, we require that

at t = 0

X = zo(s),

y = yo(s),

u = uo(s),

(1.8)

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

normal (-au/ax. -as/ay, l)

boundary curve

_$2

characteristic

characteristic projection

Fig. 1.2 Generation of the solution surface by characteristics.

then this solution surface also passes through the boundary curve. The solution

curves of (1.7) are called the characteristics;3 as a varies, the family of charac-

teristics generates a surface, as in Fig. 1.2, which we hope is the required solu-

tion surface. As also indicated in Fig. 1.2, the projections of the solution curves

of (1.7) onto the (x, y) plane are called the characteristic projections. It is not,

however, clear from this argument that the surface so constructed is smooth, or

even continuous; there might, for example, be kinks at which the derivatives of u

are discontinuous, or the surface might turn over on itself.

If the solution of the partial differential equation aOu/Ox + bOu/Oy = c is

required to be what is called a classical solution, then u and its first derivatives

must exist and make the left- and right-hand sides equal at each point. Despite the

plausibility of our geometric picture, the following analytical argument is necessary

to verify this.

Since a, b and c are functions of x, y and u but not t explicitly, the characteristic

equations (1.7) are a system of three autonomous ordinary differential equations

subject to the initial data (1.8). Now a, b and c are Lipschitz continuous, so the

Cauchy.-Picard theorem implies that the characteristic equations have a unique

local solution. Hence we may write

x = x(s, t),

y = y(s, t), u = u(s, t), (1.9)

where x(s,O) = xo(s), y(s,O) = yo (s) and u(s,O) = uo(s). Moreover, from the

same theorem, x, y and u are differentiable functions of both s and t; they also

depend continuously on the boundary data.

3We will shortly give two other important reasons for considering the curves defined by (1.7),

which will motivate new definitions of characteristics applicable to more general partial differen-

tial equations.

CHARACTERISTICS 11

The relationships x = x(s, t), y = y(s, t) and u = u(s, t) are a parametric rep-

resentation of the solution surface, which gives u locally as a unique differentiable

function of x and y if there is a unique inverse of the transformation (s, t) H (x, y).

From the inverse function theorem, the necessary and sufficient condition for this

is that

8x/8s 8x/et

x' z

# 0, 00

8y/8s y

where, here and henceforth, we write ' = 8/8s, ' = 8/8t. Using (1.7) this reduces

ay' - bx' A 0, oc,

which is certainly satisfied on the boundary curve t = 0, where it reduces to the

condition (1.5); by continuity, it is also satisfied in some neighbourhood of the

boundary. We thus have a local existence result for u. Moreover, it is trivial to

show that the function so constructed satisfies the original differential equation

a 8u/8x + b 8u/8y = c; we simply differentiate along the characteristics to give

u =c 8xx+8 y=aF+b8y

from (1.7). Note that this result shows that along a characteristic the partial

derivative terms in (1.2) reduce to a directional derivative of u in that direction.

1.3.1 Linear and semi inear equations

Although we have just derived a local existence result, there is still, of course,

the possibility that u develops singularities further away from r, and we will soon

see that this can easily happen for equations that are not linear. Linear equations

are those in which c(x, y, u) = a(x, y)u + fi(x, y) and a, b are independent of u.

The simplest example is that of kinematic waves with a = p = 0 and a, b both

constant. Then the characteristic equations are

z=a, y=b, uu=0,

so that

x = at + xo(s),

y = bt + yo(s),

u = uo(s),

which is another way of saying u = f (bx - ay) for some arbitrary function f ; the

boundary values simply propagate along the characteristic projections.

We now turn to a wider lass of equations for which the characteristic equa-

tions (1.7) can still be used easily. These are semilinear equations, defined to be

those that are linear in their principal part, namely the terms involving the highest

derivatives. Thus, for a 8u/8x + b 8u/8y = c, these equations are defined to be

such that the left-hand side, which contains all the derivatives, is linear in u in

that a and b depend on z and y alone; however, c may now depend nonlinearly on

the dependent variable u.

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

The characteristic equations (1.7) now reduce to a first-order differential equa-

tion since the equation for u uncouples and

i a'

This equation has integral curves in the (x, y) phase-plane, which are non-inter-

secting except possibly at a critical point where a = b = 0.4 Subject to the

initial conditions x(s, 0) = xo(s) and y(s, 0) = yo(s), they constitute a global

one-parameter family of curves C in the (x, y) plane, namely the characteristic

projections (often, these curves C are themselves called the characteristics). There

is a unique characteristic projection, parametrised by t and labelled by s, through

any non-critical point; hence the map (s, t) '- (x, y) is invertible there, and so

ay'-bx'#0.

Assuming the characteristic projections are known, we can calculate how u

varies along them from (1.7), using either

duc du c

whichever is more convenient. Of course, if c depends nonlinearly on u, these

last ordinary differential equations might not have global solutions, as we will

see in Example 1.3, but the fact that (1.7) has decomposed into two first-order

scalar ordinary differential equations, which can be solved sequentially, is a very

substantial simplification, even if an explicit solution cannot be found in terms of

elementary functions. The following example illustrates what can happen when we

are lucky.

Example 1.1 Solve the following linear problem:

xx+y

=(x+y)u

with

u=1 onx=1,1<y<2;

the initial data can be written in the parametric form

xo(s) = 1, yo(s) = s, uo(s) = 1

for 1 < s < 2.

In this example we expect singular behaviour to occur at x = y = 0, by analogy

with the theory of ordinary differential equations. The characteristic equations are

i=x,

y = y, u = (x + y)u,

and the characteristic projections C are given by

dy_y

As shown in Fig. 1.3, they are straight lines through the origin, which is a critical

point.

"See Exercise 1.9 for an example of behaviour near a critical point.

DOMAIN OF DEFINITION AND BLOW-UP 13

x=1

Fig. 1.3 Characteristic projections for Example 1.1.

Integrating du/dx = (x + y)u/x along a characteristic C, on which y/x is

constant, and setting u = 1 at z = 1, we have

logu = /C (1 + !x) dx =

(1 + !) (x

- 1).

J x

This solution for u is only defined in the shaded wedge in Fig. 1.3; moreover, u is

singular as x -+ 0+, a result which is also apparent if we calculate the solution in

parametric form:

x=et, y=set,

logu=(1+s)

ferd-r=(1+s)(et-1).t

With x > 0, the Jacobian (8(x, y)/8(s, t) I = -e20 is never zero, so that s and t

may be eliminated locally to obtain u as a unique function of x and y. As t -4 -oo,

(x, y) -> (0, 0), the Jacobian tends to zero, and u is singular. We will often use the

jargon blow-up as a shorthand description for singularity development in either u

or its derivatives.

1.4 Domain of definition and blow-up

In the example above, the region of x > 0, y > 0 in which the solution exists is

enclosed by the characteristic projections through the end-points of the curve in the

(x, y) plane on which the boundary data is given, i.e. the projection of the boundary

curve. This region is known as the domain of definition. If the boundary condition

had instead been u = 1, x = 1 for yl < y < y2i then the domain of definition of

the solution would have been yl < y/x < y2i x > 0. A general property for all

quasilinear scalar equations is that the domain of definition is, at the very least,

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

limited by the characteristic projections through the end-points of the projection

of the boundary curve. Further limitations on the domain of definition may result

if a and b vanish, or if u blows up as we integrate along a characteristic, or if the

Jacobian IO(x, y)/O(s, t) I vanishes on some curve in the (x, y) plane. In fact, the

domain of definition of the solution could never extend beyond such curves since,

on them, at least one of the derivatives of u is usually unbounded.

Note that the Jacobian vanishes where ay' = bx' but, in the general quasilinear

case, this limitation on the domain of definition cannot be determined without

first finding the solution u. For the semilinear case, however, &UI49x and 01U/8Y

are uniquely defined except possibly at critical points where a = b = 0, and, as

remarked earlier, the Jacobian IO(x, y)/O(s, t)I is necessarily non-zero except at a

critical point.

An example where the Jacobian vanishes on the boundary on which Cauchy

data is prescribed is the following.

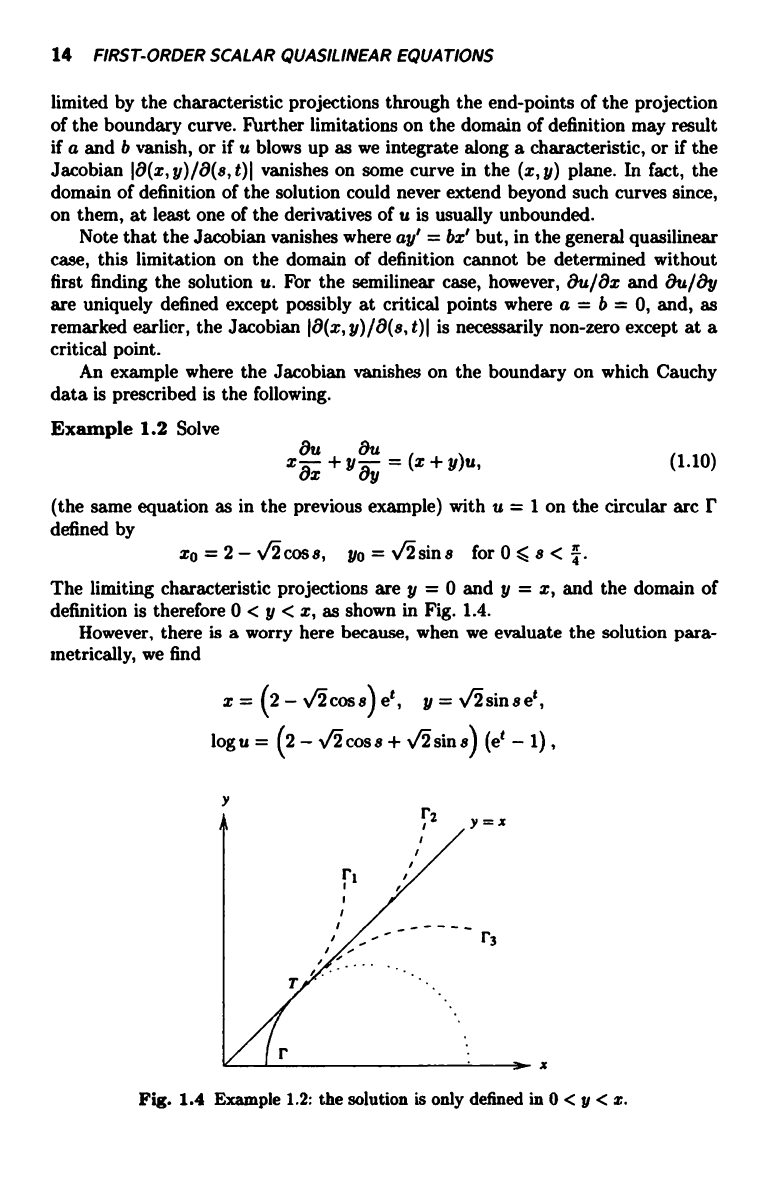
Example 1.2 Solve

x-+yT

=(x+y)u,

(1.10)

(the same equation as in the previous example) with u = 1 on the circular arc r

defined by

xo = 2 - f cos s, yo = f sins

for 0

s < 4 .

The limiting characteristic projections are y = 0 and y = x, and the domain of

definition is therefore 0 < y < x, as shown in Fig. 1.4.

However, there is a worry here because, when we evaluate the solution para-

metrically, we find

x= (2-vcoss)et,

y= fsinset,

log u = (2 - cos s + v sin s) (et - 1)

Fig. 1.4 Example 1.2: the solution is only defined in 0 < y < x.

QUASILINEAR EQUATIONS 15

and hence

x'y-y'i=2e2t (i- fcosa);

although this expression is non-zero for 0 < s < 7r/4, it vanishes where r is

tangent to the characteristic 8 = it/4. This sends us a danger signal, not for the

problem (1.10) as it stands, but for any problem in which we might attempt to

continue the Cauchy data up to or beyond the point T in Fig. 1.4. If we were to

continue on 1'1i we might only have problems on the characteristic y = x, but if

we tried r2 (any curve containing a segment of the characteristic y = x) or r3,

we would almost certainly pose ourselves a problem with no solution at all. In

the case of F2i our data would probably violate the characteristic equations (1.7),

and for r3i which meets the characteristic projections passing through r, the

data would probably be inconsistent with the information propagating along the

characteristics from F.

It is well known that the solutions to first-order nonlinear ordinary differential

equations can easily blow-up by developing singularities. The same can therefore

happen for semilinear equations, as the following example shows.

Example 1.3 Solve

8u 8u 2

8x+u

inx>0

with

u = e-v on x = 0, i.e.

x0=O,

YO=s,

uo = e '

Clearly, the parametric form of the solution is

x=t, y=t+s, u=e

The nonlinear right-hand side of (1.11) is so strong that the solution blows up,

with u -* oo, on the curve x = ein-02. The domain of definition is the region

where x < e(y-z)2; there is no obvious way to define u beyond this region without

some drastic modification to our partial differential equation.

This kind of behaviour is rarely encountered in practice for first-order scalar

equations, but we will see many examples of it for higher-order equations in Chap-

ter 6. However, there is another more endemic kind of blow-up that occurs for

quasilinear first-order equations, to which we now turn.

1.5

Quasilinear equations

The general theory of integrals of three autonomous ordinary differential equations

z = a, U = b and u = c is much more difficult than that for the two such equations

which were obtained in the linear or semilinear case. Indeed, the extra degree

of freedom enjoyed by three-dimensional phase-spaces compared to phase-planes

means that we must be prepared for chaotic characteristics and hence `wrinkled'

integral surfaces, if indeed the integral surfaces can be defined at all. We therefore

begin by looking at quasilinear partial differential equations by example.

FIRST-ORDER SCALAR QUASILINEAR EQUATIONS

When it comes to writing down explicit solutions, we may be fortunate enough

to encounter an equation as symmetric as

x(y - u) 8x

+ y(u - X) FY =

u(x - y),

in which case it is easy to spot integrals of

dx dy du

x(y - u) y(u - x) u(x - y)

in the form'

x + y + u = xo(8) + yo(s) + uo(s),

xyu = xo(s)yo(8)uo(8),

so that the characteristic projections are given by

x + y +

zo(8)yo( )uo(8)

= xo(s) + yo(s) + uo(s)

(1.12)

(1.13)

From the practical viewpoint, there is another serendipitous approach to the

characteristic equations which is often more convenient than working with the

parametric representation in terms of a and t. This is to note that, if we can spot

two independent integrals f (z, y, u) = constant and g(x, y, u) = constant, then the

general solution of the original partial differential equation (1.2) is G(f, g) = 0,

where G is arbitrary. To see this, note that the surface G = 0 meets a surface

f = c where G(c, g) = 0, i.e. where g = constant; hence the surface G = 0 is

composed of characteristics in accordance with Fig. 1.2, and this reflects the fact

that any two integral surfaces intersect in a characteristic. Clearly, the solution to

the example above can be obtained in this way, with f = xyu and g = x + y + u;

see Exercise 1.4. However, at the end of the day, the existence of explicit solutions

is a rare event indicative of some underlying symmetry which may be difficult to

discern; we will return to this general question in Chapter 6.

Parametric solution representations such as (1.13) may conceal a phenomenon

which can be studied conveniently by the simpler prototype

On On

8x+u8i=0. (1.14)

This is a kinematic wave in which z plays the role of time; the wave speed de-

pends linearly on the wave amplitude u, rather than quadratically as in the paint

model (1.1). We can get a good idea of what might happen here by watching waves

run up a shallow beach, where water at the crest of a wave moves faster than at

51n this context the componendo et dioidendo rule

61 - 62 - -Qn - A

-bl - bs -

E,Atbi

for any A,, is often useful.

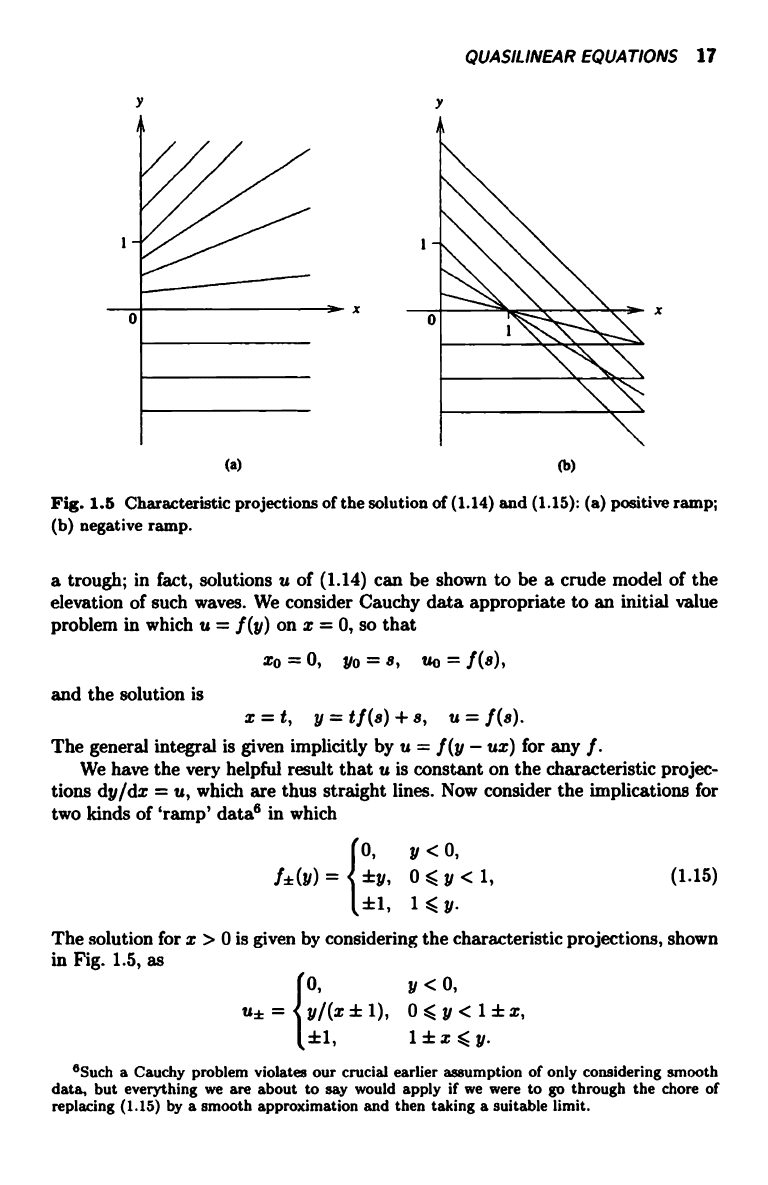
QUASILINEAR EQUATIONS 17

(a)

- x

(b)

Fig. 1.5 Characteristic projections of the solution of (1.14) and (1.15): (a) positive ramp;

(b) negative ramp.

a trough; in fact, solutions u of (1.14) can be shown to be a crude model of the

elevation of such waves. We consider Cauchy data appropriate to an initial value

problem in which u = f (y) on x = 0, so that

x0 =0, yo=8, uo=f(a),

and the solution is

x=t, y=tf(8)+8, u= f(8).

The general integral is given implicitly by u = f (y - ux) for any f .

We have the very helpful result that u is constant on the characteristic projec-

tions dy/dx = u, which are thus straight lines. Now consider the implications for

two kinds of `ramp' datas in which

y < 0,

ft(y) =

±y, 0

y < 1,

(1.15)

t1, l

The solution for z > 0 is given by considering the characteristic projections, shown

in Fig. 1.5, as

10,

y < 0,

ut= y/(xf1), Oy<l±x,

fl, 1fx'< Y.

6Such a Cauchy problem violates our crucial earlier assumption of only considering smooth

data, but everything we are about to say would apply if we were to go through the chore of

replacing (1.15) by a smooth approximation and then taking a suitable limit.