Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

368

NON-QUASILINEAR EQUATIONS

The solution breaks down at the apex, as may be confirmed by evaluating the

Jacobian I8(x, y)/8(s, t)J in the form

2py' - 2qx' = 2(2t(q po

- goA) + yopo - xogo) = 2(2t - 1).

This vanishes when t = 1/2, u = 1 and x = y = 0, thus limiting the domain of

definition to t < 1/2, the interior of the circle minus the centre.

For an elliptical base, we write xo = a cos s and yo = b sins, with a > b, and

po = - cos 0 and qo = - sin 0, where b tan 8 = a tan s. To avoid the algebraic

complexity of a direct elimination of a and 0, we just consider the ray pattern. A

typical ray has equation

y - b sin s = tan 8(x - a cos s),

a > b > 0, (8.26)

and intersects y = 0 and, by symmetry, at least one other ray, where x =

((a2 - b2)/a) cos s. Thus the solution breaks down on y = 0, JzJ < (a2 - b2)/a,

and the surface has a 'ridge line'. The height of this ridge line is tedious to find,

but at x = 0, where s = 7r/2 and 0 = 31r/2, u = b; at x = (a2 - b2)/a, s = 0and

8=zr,sothat u=b2/a.

The discussion above has an intuitive component because of our bald assertion

that a ridge line exists. This clearly accords with everyday experience with, say, a

spoon heaped with fine dry sugar, but in the next example we will see that there

are other mathematical solutions of (8.1) which do not 'stop' at the ridge. In fact,

the ridges are reminiscent of the shocks we encountered in the quasilinear theory

of Chapters 1 and 2, and we will have more to say about their mathematical status

shortly.

8.2.3.2

Geometric optics

Since geometric optics is described by the same equation as that for sand piles, it

might be thought that there is nothing more to say about it. However, the physical

interpretation of the dependent variable is so different that a separate theoretical

development is necessary.

The characteristic projections of (8.1) in the (x, y) plane, which are of course

straight lines, are called light rays in the geometric optics applications. They are

parallel to Vu and hence are normal to the level sets of u which are the contour

lines in the sand pile example. However, if we return to the time domain, as in (8.2),

it is natural to define a wave front as a level curve of the phase of 0.189 Hence,

remembering the definition of u in (8.4), if u = uo defines a wave-front at r = ro,

and (xo, yo) is a point on it, then, at a later time Ti, the wave-front is given by

u = ul = u0 + rl - -r0; it is the projection in the (x, y) plane of the envelope of the

integral conoids (Monge cones in this case) evaluated at u = ul, namely

(x - x0)2 + (y - yo)2 = (ul - 'uo)2 = (rl - 7o)2,

(8.27)

where xo and yo vary over the wave-front at r = ro. As in Fig. 8.3, (8.27) represents

a family of circles of prescribed radius and this is called Huygens' construction. If

""This is in accord with the nomenclature in §4.6.

SCALAR FIRST-ORDER EQUATIONS 369

wave-fronts at r = rl

Fig. 8.3 Huygens' construction.

the wave speed is not constant, say if the medium has variable refractive index,

then k is a function of position, the rays are curved and Huygens' construction

only holds for small time intervals.

Two serious difficulties must be addressed before we can begin to use geometric

optics to represent solutions of practical interest in wave propagation. The first

concerns a phenomenon that we have already encountered in our study of sand

piles, namely the intersection of characteristics. In optics, the interpretation of

characteristic intersection differs fundamentally from that in Chapter 1 and at the

end of the previous example. In both these latter situations, the dependent vari-

able was required to be single-valued, and hence the intersection of characteristics

motivated the introduction of a shock or ridge, respectively. However, for wave

applications there is no restriction that the phase u should be single-valued nor

even that it should be real (which leads to another topic to be mentioned later).

Indeed, since there is no reason why many waves should not exist at any point,

we can happily continue our characteristics through any intersection point, and

in general they form an envelope'60 called a caustic. A famous example is the

solution of Charpit's equations for IVul2 = 1, with data

uo = s on x0 = cos s + sins, yo = sin s - cos s, (8.28)

a circle of radius f. We soon find that

p = p0 = - sins or p0 = cons,

q=qo=toss

or qo=sins,

and, redefining the parameter t so that dx/dt = p, etc.,

16°In special cases, of course, the rays may 'focus' at a point, but such a geometry is not stable

to small perturbations. Stable envelopes can be classified using catastrophe theory [1].

370

NON-QUASILINEAR EQUATIONS

Fig. 8.4 Circular caustic in a circle.

x = cos a - (t -1) sin 8

or x =sins + (t + 1) cos s,

y =sins + (t - 1) cos s or

- cos s + (t + 1) sin s,

u=s+t,

respectively. There are two values of po and qo corresponding to any value of a,

and the rays envelop a circular caustic on x2 + y2 = 1, as shown in Fig. 8.4.

In this situation the caustic separates a region of greater illumination, x2+y2 >

1, through each point of which there are two rays, from one of less illumination,

a.2 + y2 < 1, where there are no real rays, and all caustics share this attribute of

separating brighter regions from darker ones."' However, the one that is easiest

to see in practice is the nephroid formed by sunlight reflecting from the curved

vertical side of a nearly-filled coffee mug; here the bright region has four rays

through any point and in the dark region there are just two rays through any

point (see Exercise 8.8 and Fig. 8.8).

The bunching of the rays in Fig. 8.4 suggests that the region of greatest illu-

mination is near the caustic. To see this more precisely, we note that, in general,

the solution

x = Po(s)t + xo(s), y = go(a)t + yo(s),

u = t + oa(s), (8.29)

where

dxo dyo

duo

p02 +

= 1

and

d.R ds q0 - ds

yields a Jacobian (see Exercise 8.11)

8(s,)

(goPo - Poq') (t + T (s))

where

"'This is because, as we shall see, the field inside the caustic is exponentially small in the

parameter k in (8.4).

SCALAR FIRST-ORDER EQUATIONS 371

T (s) =

goxo - Poyo

goroo - pogo'

Hence, unless gopo = poq'o, which only happens for plane waves in which u is real

and linear in x and y, there is always a caustic at t = -T(s). Now this has serious

implications for the amplitude A in (8.4). By equating terms of 0(k) to be zero

in the ansatz there, A satisfies

AV2u + 2Vu VA = 0.

(8.30)

This linear partial differential equation for A has an explicit solution by the meth-

ods of Chapter 1; following Exercise 8.11, we find that

A(8) = Ao(8)

T (s)

t + T(s) '

(8.31)

indicating an increased illumination as t -* -T(s). In the example (8.28), T = -1

and A has an inverse square-root singularity as t t 1. This is clearly a warning

that the geometric optics ansatz has broken down and we must make a different

high-frequency approximation to Helmholtz' equation near the caustic, but this

would not be in the spirit of the book.162

A less symmetric example of a caustic has just been encountered in the el-

liptic sand pile solution (8.26). Continuing the characteristics through the ridge

lines gives the ray picture shown in Fig. 8.5, and it soon becomes clear that caus-

tics develop cusps whenever a boundary with constant Dirichlet data for u has a

maximum or minimum in its curvature (see Exercise 8.9).

In summary, the problems created by intersecting characteristics for wave prob-

lems are more innocuous than when u is required to be single-valued. Although

the caustics perturb the ray model locally, they do not affect the solution globally

in the way that shocks or ridge lines do.

Our second serious difficulty with practical ray theory occurs when we consider

configurations that involve physical boundaries. One of the commonest concerns

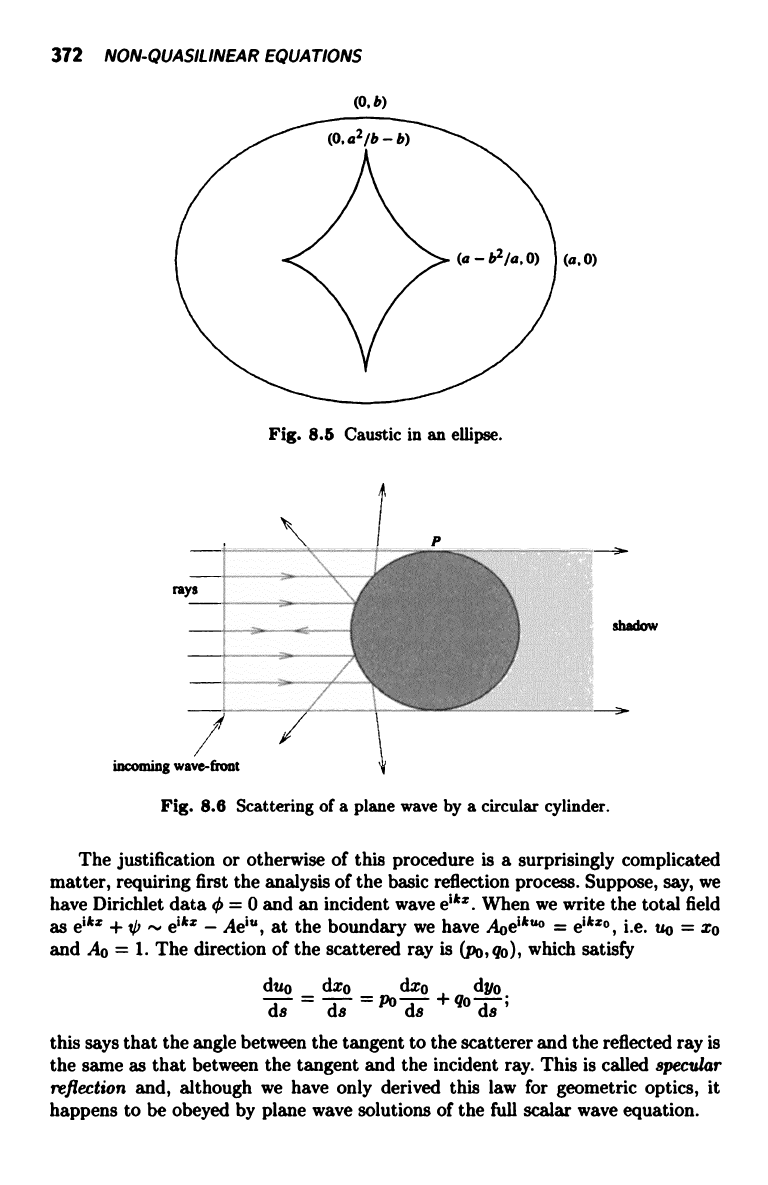
the scattering of a plane wave, say with rays parallel to the x axis and wave-

fronts parallel to the y axis, by a smooth convex obstacle163 (see Fig. 8.6) at

which Dirichlet or Neumann conditions are imposed. This situation might arise

in tomography, radar or ultrasonic testing and, at first sight, all we have to do is

follow the familiar rules of optics and draw the reflected rays, as in Fig. 8.6.

'62Those who may doubt the geometric optics approach may, in this case, look at the function

=Jk (k x2+y2)exp(iktan-'

which is an exact solution of Helmholtz' equation, and take the limit as k -, oo; the solution

corresponding to (8.28) is the asymptotic limit of t/,eik*I4 for x2 + y2 > 1, as long as we are not

close to the caustic.

isWhen the scatterer is a circular cylinder, it is possible to write down the reflected field exactly

by separating the variables. Unfortunately, the asymptotic form of the eigenfunction expansion,

which involves H,il l (kr) cos n9, is not easy to find.

372

NON-QUASILINEAR EQUATIONS

(0, b)

(a, 0)

Fig. 8.5 Caustic in an ellipse.

Fig. 8.6 Scattering of a plane wave by a circular cylinder.

The justification or otherwise of this procedure is a surprisingly complicated

matter, requiring first the analysis of the basic reflection process. Suppose, say, we

have Dirichlet data 0 = 0 and an incident wave eikz. When we write the total field

eikx

+ tai ,

eik:

- Ae1", at the boundary we have Aoeikun =

eikzo, i.e.

u0 = xo

and A° = 1. The direction of the scattered ray is (po,qo), which satisfy

duo dxo dxo

dyo

a8 = a8 =

p°

a8 + q° ds

this says that the angle between the tangent to the scatterer and the reflected ray is

the same as that between the tangent and the incident ray. This is called specular

reflection and, although we have only derived this law for geometric optics, it

happens to be obeyed by plane wave solutions of the full scalar wave equation.

SCALAR FIRST-ORDER EQUATIONS 373

This argument works in general unless the scatterer has corners or, as at P

in Fig. 8.6, the ray is at `grazing' incidence. 164 In either case, modifications have

to be made to the geometric optics ansatz which are much too complicated to be

discussed here, but form the basis of J. B. Keller's Geometric Theory of Diffraction

[5]. The modifications are by no means local to the body, involving, for example,

the shadow boundaries. Also, if the scatterer has any concavities, then caustics

are almost inevitably present.

We conclude this brief discussion of a very large subject with three remarks.

First, there is no reason why we should not apply a WKB-style ansatz to the full

wave equation rather than considering the single Fourier component (8.2). There

is then no large parameter k in which to expand asymptotically, but we can justify

the procedure in cases where the wavelength is much smaller than the length scale

over which we are considering the solution. Thus, writing

where Vu is large, we obtain

/2+ \5i/2

(8r)2.

(8.32)

This equation can, of course, be solved by Charpit's method (see Exercise 8.12),

but it is precisely the equation for the characteristic surfaces of the two-dimensional

wave equation, as given in a different notation in §2.6. Thus, the geometric optics

approach coincides with our theory of characteristics, as has already been evident

from the discussion of rays and wave-fronts in this chapter and Chapter 4; the

rays are simply the bicharacteristics associated with Charpit's method. However,

geometric optics has the advantage of being susceptible to improvement by in-

cluding the effects of longer wavelengths, because we can proceed to compute A

in (8.4) as a series in inverse powers of k; the theory of characteristics is merely

the 'zero-wavelength' limit.165

Secondly, there is no reason why we should not apply geometric optics to the

modified Helmholtz equation

(V2

k2),0 = 0.

(8.33)

We have already seen that this equation describes physical problems that are quite

different from wave propagation, yet, by setting tG - Aek", we obtain (8.1) again!

However, the difference between the physical interpretation of (8.33) and (8.3) has

already emerged: for problems for which (8.33) is the correct model, u must be

single-valued and hence the `ridge line' solution would be the appropriate one for,

164Note that the breakdown of the ray solution at P can be likened to that near a caustic

because two rays, one incident and one reflected, coincide at P.

165However, we must remember the situation mentioned in Chapter 4, where a highly localised

initial condition for the wave equation could create an equally localised response near the char-

acteristics emanating from the source, and also a non-trivial response away from these charac-

teristics.

374

NON-QUASILINEAR EQUATIONS

say, a chemical reaction occurring in an elliptical container, as in (8.26). More-

over, starting from (8.33), we could carry out a 'shock'-type analysis of the ridge

structure in the same spirit as in Chapters 2, 6 and 7 (see Exercise 8.14).

Finally, we mention what is perhaps the most challenging aspect of geomet-

ric optics. This is the fact that u does not have to be real for (8.1) to apply to

wave propagation, although a complex u would correspond to 0 being either ex-

ponentially large or exponentially small. We can see a hint of this in our simplest

example (8.28) because, if s and t are such that x2 + y2 < 1, then it is easy to see

that u is complex. But such values of a and t are also complex and this means that

we are led to the idea of complex rays, in which x and y must also be complexified.

Further discussion of this subject, which is not at all well developed, cannot be

given here.

*8.2.4

Eigenvalue problems

The application of geometric optics to find high eigenfrequencies using Helmholtz

or other wave-related equations turns out to be surprisingly difficult and delicate.

We will content ourselves with describing one simple example which will be of

great motivational value in the next section.

Suppose we wish to find large values of A such that the problem

V21p

+ At = 0

(8.34)

in the circle

x2 + y2 C R2,

with either homogeneous Dirichlet or Neumann boundary data, has non-trivial

solutions, i.e. -A is an eigenvalue of V2. Let us assume that A is large enough that

we can approximate i' in the form

+G(x, y; A) - A(x,

y)e'JXL(=.v),

where u satisfies IVu12 = 1. The phase u can only be determined from Charpit's

equations if we know its value at the boundary. This data determines 8u/8& and

±Ou/8r in polar coordinates. Since the ray is in the direction of Vu, the com-

ponents of Vu are (sin 0, cos 0), also in polar coordinates, where 0 is the launch

angle of the two possible rays through any point P on the boundary, as shown in

Fig. 8.7. On each of these rays, near P, the two phases are

ut -rup+R(8-8p)cos¢f (R-r)sin0+ .

We must satisfy the boundary condition ' = 0, and, since we cannot do this

by taking A = 0 on r = R (as then A vanishes everywhere), we achieve this by

setting

',(x, y) = A(x, y) (ei'u+ -

e'vf%u- )

The only potential problem with this procedure is that the `+' ray might, after

a number of bounces as in Fig. 8.7(a), return to P as a '-' ray, bringing with it

SCALAR FIRST-ORDER EQUATIONS 375

(a)

(b)

Fig. 8.7 Eigenvalues of the Laplacian in a circle.

a value of u+, obtained by integrating Charpit's equations along this ray, that is

inconsistent with u_ at P. This consistency requirement will lead to the deter-

mination of the eigenvalues. Now for most values of 0, namely those for which

cos-1(Ro/R) is an irrational multiple of zr, where RD is as in Fig. 8.7(b), this does

not occur. However, we must also recognise that the rays launched at the angle 0

from different points on the boundary have an envelope (caustic) with radius Ro

(see Fig. 8.7(b)), which is itself a route along which the phase u+ can travel. Thus

we must consider trajectories such as that from P to Q, around the caustic any

number of times ending at Q', and back to P. When we work out the change in

u+ along such a trajectory, it must be an integer multiple of 27r if we are to be

consistent with u_ at P. After a simple calculation, this leads to the conditions

2aRof = 27rni,

(8.35)

2v (R2

- Ro -

cos-1 (R))

= 21r%,

(8.36)

for some integers n1 and n2. Finally, we are led to the requirement that the eigen-

value \ is such that the eliminant of Ro between equations (8.35) and (8.36) is

satisfied for some integers n1 and n2. It can be shown that this gives a good ap-

proximation to the n2th zero of the Bessel function J,,, (fR) that appears in the

exact solution of (8.34).

Unfortunately, this is not an easy technique to use on more general prob-

lems. Even a slight modification to the boundary can lead to formidable geometric

and analytical difficulties in ray tracing. Furthermore, any attempt to increase

the accuracy of results by including the amplitude A as well as u becomes quite

complicated. One inaccuracy in (8.35) is immediately apparent because we have

assumed that u is continuous when a ray grazes the circle r = RD. In fact, a local

calculation of the type mentioned after (8.31) shows that u always changes by it/2

at a grazing point, and hence n2 in (8.36) should at the very least be replaced by

n2 + 1/4.

One insight we may gain from this ray analysis concerns the qualitative be-

haviour of the eigenfunctions corresponding to the large eigenvalues. Figure 8.7(b)

376

NON-QUASILINEAR EQUATIONS

suggests that the eigenfunctions corresponding to the launch angle 0 will be 1o-

caused near the caustic r = Ro. Were we to try a similar analysis in a rectangular

domain, the absence of any caustics suggests that the eigenfunctions are not lo-

calised in this geometry, as can be verified by considering their exact representation

in terms of trigonometric functions.

8.2.5

Dispersion

The ideas described above are by no means confined to (8.1). Indeed, general

models involving linear partial differential equations for wave propagation with

constant coefficients have solutions in which the dependent variables are all pro-

portional to e'(k.x-"'), as long as some dispersion relation

F(k, w) = 0 (8.37)

holds between the wavenumber vector k and the frequency w. This approach to

dispersion is simply a repetition of the ideas of §7.2.1; the fact that the model

permits wave solutions at all means that there are real values of k and w that

satisfy (8.37). For linear problems, the property that a model admits a dispersion

relation with real k and w is another approach to hyperbolicity, as defined in §3.3.

It has the advantage of applying to models, such as that for surface gravity waves

in §7.2.1, which contain more information than just partial differential equations;

for instance, F could be crucially dependent on the boundary conditions, as in the

example below.

The theory of this chapter has a really useful role to play when we apply the

WKB methodology to linear wave propagation models by writing all the depen-

dent variables in the form Ae'k". The highest derivatives are the only relevant

terms because, as stated above, the restriction of the WKB approach is that the

wavelength is much less than any length scale of interest, and thus it is a `short

wavelength' or 'far-field' approximation. In any case, the operator 8/8xj is equiv-

alent to multiplication by ik,, and (8.37) implies that u satisfies

F,-

f = 0.

(8.38)

For the simple example (8.32), it is easily seen from Charpit's equations that,

not only are the components of Vu and 8u/Or constant along characteristics, but

also that u itself is constant. The fact that the phase u does not change along

a characteristic (or ray) results from the fact that all disturbances, no matter

what their frequency or wavelength, travel at the same speed. Hence there is no

dispersion, i.e. no `mixing' of waves of different wavelengths.

An example in which dispersion is important is the famous problem of the

far-field of the wave pattern created by a ship travelling with speed V in the x

direction on an infinitely deep ocean. As shown in Exercise 8.15, the dispersion

relation is

(-w+Vkl)° =92(ki +k2),

(8.39)

where x and y are horizontal coordinates in the ocean surface, g is the acceleration

due to gravity and k = (kl, k2). Hence, in the steady state in which w = 0, the

WKB approximation for the phase u of the surface elevation satisfies

SCALAR FIRST-ORDER EQUATIONS 377

V4p4 = g2(p2 + q2),

(8.40)

where, as usual, p = Ou/Ox and q = Ou/Oy. Now, in the WKB approximation, the

ship is effectively a point, say the origin, and hence we are only interested in the

integral conoid through it, which is given by

x. = (41 *4p3 - 2g2p)t,

y = -2g2gt,

u = 2V4p4t,

together with (8.40). The most striking feature emerges when we consider the ray

slope, which is -pq/(p2 + 2q2) for any value of V (or g), and has a maximum of

1/(2vr2). Hence the waves are confined to a wedge of semi-angle sin-' (1/3), within

which there are two curved wave-fronts through any point touching on the wedge,

each carrying a different phase. The limiting straight rays are caustics at which

the Jacobian vanishes, and there a large-magnitude `bow wave' is seen, as shown

in the photograph in [45, p. 117].

8.2.6 Bicharacteristics

One bonus of the m,-dimensional generalisation of the situation of Fig. 8.1 is that we

are now in a position to construct the bicharacteristics of m-dimensional hyperbolic

equations, as introduced in §2.6, of the form

8a';

Indeed, the fact that the characteristics satisfying (8.22)-(8.24) yield the genera-

tors of the Monge cone locally means that we only have to find the characteristics

of (2.53), namely

det E A

= 0.

Thus, for the wave equation

82u

_ 2

82u

at2

(02U

YX- + aye

)

we need the characteristics of

((ax)z+(ay)2/

-Cam/2'

which, with ao = 1, is (8.32). For the characteristic cone through the origin, these

are simply the generators

x=pr, y=qr,

t=rr,

where

p2+q2=aor2,

but the geometry can easily become more complicated (see Exercise 8.13).