Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

348

FREE BOUNDARY PROBLEMS

The situation is more interesting in three dimensions when (7.110) becomes

curl v = 8r (x - X(s, t)),

where x = X(s, t) describes the vortex curve r at time t, and the vector delta

function is defined in terms of scalar delta functions as

d(x - x') dx'.

br(x) =

Now, referring back to (4.77), we find that

(7.112)

v(x't)

4rr r

)

Ix - x'1

J (

and, to make further progress, we must study the behaviour of v as we approach

r.155 Unfortunately, (7.112) is singular as x -1' r and a tedious calculation is

necessary to show that, when we are a dimensionless distance d from r,

1 _ (logd)

2adea 47r

1 rcb +

where ee is a local azimuthal vector, k is the principal curvature of I' and b is the

binormal. Hence, if we follow (7.111) and assert that the velocity of r is governed

by the regular part of the locally induced flow, then the vortex velocity yr is

governed by the partial differential equation

(log do) nb

(7.113)

when do is some `cut-off' that needs to be preassigned.156 What has happened is

that the intensity of the singularity at the vortex is so strong that it controls its

motion independently of any externally-imposed velocity field, in sharp contrast

to typical models for codimension-one problems. We note also that (7.113) is a

generalisation of the equation of curvature flow (6.88) and its only known exact

solution is a rotating helix given parametrically by

x= (acos(s-wt),asin(s-wt),b(s-Vt)), (7.114)

where a and b are constants and the constant rotation rate w and translation speed

V are related as shown in Exercise 7.21. When w = 0 and b -+ 0 with bV finite,

this solution represents a `smoke ring', and we will return to it in §9.2.3.

115 Had we adopted this approach for any of the codimension-one problems described earlier,

say by using the integral representation (7.68), we would have found well-defined limits as we

approached r from either side and hence the jump conditions with which we have become familiar.

156This device of introducing a cut-off can be thought of as a physical regularisation of the

singularity that would occur if do = 0.

EXERCISES 349

Exercises

7.1. Consider the Stefan problem

02u

8t = 8x2'

with

u=0 and

at z = s(t), and

x 0 8(t),

s(0) = 0,

u(x,0)

no = constant,

x < 0,

u, = constant, x > 0.

Show that there is a solution u(x, t) = U(i1), where n = x/f and s(t) = af,

as long as

e-9'/4

d9 I -

+ ui (f.00 e-11

2 /4

d17 I

= 0.

e°2/4 +

uo (

foo

When uo = 0, use the result that ae°' /4 f, e-n'/4 di, is monotone and tends

to 2 as a - oo to show that there is a solution for a if ul > -1 but not if

u, <-1.

Remark. The Stefan condition as written here, with a latent heat of 1, forces

the liquid to lie in x > s(t) and the solid in x < s(t). The liquid is supercooled

and solidifies (a > 0) if uo = 0 and -1 < ul < 0. Likewise, the solid is

superheated and melts if ul = 0 and 0 < uo < 1. The non-existence of

solutions for ul < -1 or uo > 1 is discussed in §7.5.1.

7.2. Suppose, in a Muskat problem, V2pU, = 0 on one side of an interface and

V2po = 0 on the other side (see §7.1.1). Also suppose that gravity is negligible

and that the free boundary conditions are e-'8p,,/8n = Op./On = -vn,

where 0 < e QC 1. Write p,,; = ep,.,o +

, po = poo +

and equate

coefficients of e to show that poo satisfies the Hele-Shaw problem

O2poo = 0

with

Poo = 0,

-vn

at the free boundary. What problem does p,,,o satisfy?

7.3. Consider the one-dimensional obstacle problem with a smooth concave ob-

stacle f (x), where f is even, f (0) = 0 and d2 f /dx2 < 0. Consider the linear

complementarity formulation of p. 331,

d2u

dx2

50, u - f 3 0,

(u-f)2 =0,

with u(-1) = u(1) = 0. Suppose that the contact region is -x' < x < x'.

Assume that, as can be justified using the theory of distributions, we can

write

350

FREE BOUNDARY PROBLEMS

Z.+ dzu

. _

dx2

dx =

Show that, if the right-hand side of this equation is positive, then we do not

have dzu/dxz < 0. Show also that, if the right-hand side is negative, then

we cannot have u - f > 0. Deduce that du/dx is continuous at x = x'.

* 7.4. Consider an American put option as in §7.1.2, with optimal exercise value

S*(t),and V(S,t)=E-Sfor 0<S<S'(t).

(i) Suppose that at time t the option is alive and S falls to S* (t). Show that,

if lim 515. V (S, t) = E - S* (t) + A, where A > 0, then after the next time

step dt the option should be exercised with probability 1/2 + O(dt) for

a profit of A + O( dt), while with probability 1/2 + O(dt) its value will

change by only O( dt). Deduce that arbitrage forces V to be continuous

atS=S*.

(ii) Now suppose that S = S' as in part (i) and that OV/8S (S", t) <

-1. Show that the option value falls below the payoff for values of S

just above S' and explain why this is impossible. Finally, suppose that

8V/8S (S', t) > -1, and show by a sketch of V as a function of S that

the option value would be greater if S' were smaller, and that taking

S' smaller would decrease the value of 8V/8S (S', t). Deduce that the

option has its maximum value to the holder if S' (t) is chosen to make

8V/8S continuous there.

7.5. The linear complementarity form of the American put option problem of

p. 334 is

G4' =

2a222 8S2

+ rS 85 - rV < 0, V - max(E - S, 0) > 0,

(,CV) (V - max(E - S, 0)) = 0,

together with V(S, T) = max(E - S, 0). Adapt the argument of Exercise 7.3

to show that 8V/8S is continuous at the optimal exercise boundary S =

S" (t).

* 7.6. Slow viscous flow in two dimensions is modelled by

pV2u

= Vp, V u = 0,

where p = constant, u = (u, v) and the force per unit area on a surface with

normal n is

(-p + 2p 8u/8x p (8u/8y + 8v/8x)

p (8u/8y + 8v/8x)

-p + 2p Ov/8y

(n2)

Show that

EXERCISES 351

(i) there is a tJ such that

a1U aV,

, v=-ax,

and that

04'1(1 = 0;

(ii) there is an .4 such that

-p+2µ0a =-2µaa

-p+2µ' =-2paa-z,

tax

(&U

02A

(8y + ax)

2µ

ax ay'

and that

V4A=0.

In a steady slow flow with a stress-free free boundary r, show that 1/J =

constant and alas(VA) = 0 on r, where a/Os denotes the derivative along

r. Show that this implies A = constant and OA/01n = 0 on r. In what

geometries can .4 be set equal to zero on r without loss of generality?

* 7.7. Suppose there is a constant surface tension in the slow flow of Exercise 7.6 so

that the force per unit area on the free surface is -T1cn, where T = constant

and K is the curvature. Show that, without loss of generality,

A = constant,

OA = T

an 2µ'

7.8. Suppose a smooth rigid indenter y = f (x) displaces a smooth elastic half-

space by a small amount over the region lxi < c. Denote the force per unit

area on the boundary of the half-space by

Cr2

a.) (1)

Formulate boundary conditions for the displacement (u, v) and forces on

y=0as

ay = r = 0,

v < f(x)

for jxj > c,

T=O.

v = f(x),

oy < 0

for lxi < c.

Write these conditions in linear complementarity form.

7.9. Suppose that

aU _ 0211

for0<x<s(t),

at axe

with

352

FREE BOUNDARY PROBLEMS

u=0, 8 =-s atx=8(t),

5x(O,t)

= 0

and

u(x,0) = uo(x) < 0

with

8(0) = 80.

Show that

a(e)

282 + f

xu(x, t)

dxl = u(o, t) , 0,

and hence that, if

2so + fo

xuo(x) dx < 0,

hen neither can there be a steady state in which u = 0 and s > 0, nor can

8 vanish.

Remark. This method of proving blow-up can be extended to functions

(1(8)

+ f

f'(x)u(x, t) dx)

as long as f has suitable properties.

* 7.10. Show that

lim

a (x-t)'/4t

dt =

e -t/4

s f

and that

f'e-(.-t)'14t

_ - 2 f.(x -

tdt

for

x > 0.

However, show also that this last derivative at x = 0 is not equal to

1 f°°

e t/4 dt

2 o

Remark. It can be shown that

e_(x_t)2/4t dt

t e

f (

0=f

rf (0),

_t/4 dl t -

7tZOO

which explains the factor 1/2 on the left-hand side of (7.68).

7.11. A circular membrane has zero transverse displacement on the circle x2 +

y2 = 1, z = 0, but it is constrained to lie above the smooth obstacle z =

e(1 - 2(x2 + y2)), where e is small and positive. Show that the radius R of

the contact region satisfies 2R2(1- 2 log R) =1.

EXERCISES 353

7.12. The conditions ahead of (0) and behind (1) a gasdynamic shock moving with

speed V. are related by (2.49), namely

[p(Vs - uAo = (p + P(Vs - u)2)

P(V, - u)

(

1(V,

- u)2

L \(1'-1)P

)10

= 0.

Deduce that, if a piston moves with speed Vp into a tube of stationary gas

in which p = po and p = po, then the free boundary (shock) has speed V

where

V2-7

+2 1

VPV,-ao=0, ao=.

220

* 7.13. Show that the Rankine-Hugoniot conditions of Exercise 7.12 imply

(ui - uo)2 = (Pi - Po)

(I-

and

(7 + 1)Po + (_- 1)P1

Po P1 Pi

(7 - 1)Po + (7 + 1)P1

Deduce that, if a shock wave with pressure pi behind it propagating into

stationary gas in which p = po and p = po reflects from a plane wall to

which it is parallel, then the pressure behind the reflected shock is p2, where

((3-1

- 1)

- (7 - 1)J

Of -1)L- + Of + 1)

* 7.14. A two-dimensional jet of inviscid irrotational fluid, of thickness 2h00 and

moving to the right with speed 1, enters a semi-infinite rectangular cavity

with walls at y = ±1, as shown in Fig. 7.11; the y axis is tangent to the free

surface.

Ignoring gravity and surface tension, show that the boundary value problem

for the complex potential w(z) = 0+i ti for the upper half of the flow is that

w(z) is analytic in the fluid region, with

Fig. 7.11 A jet entering a box.

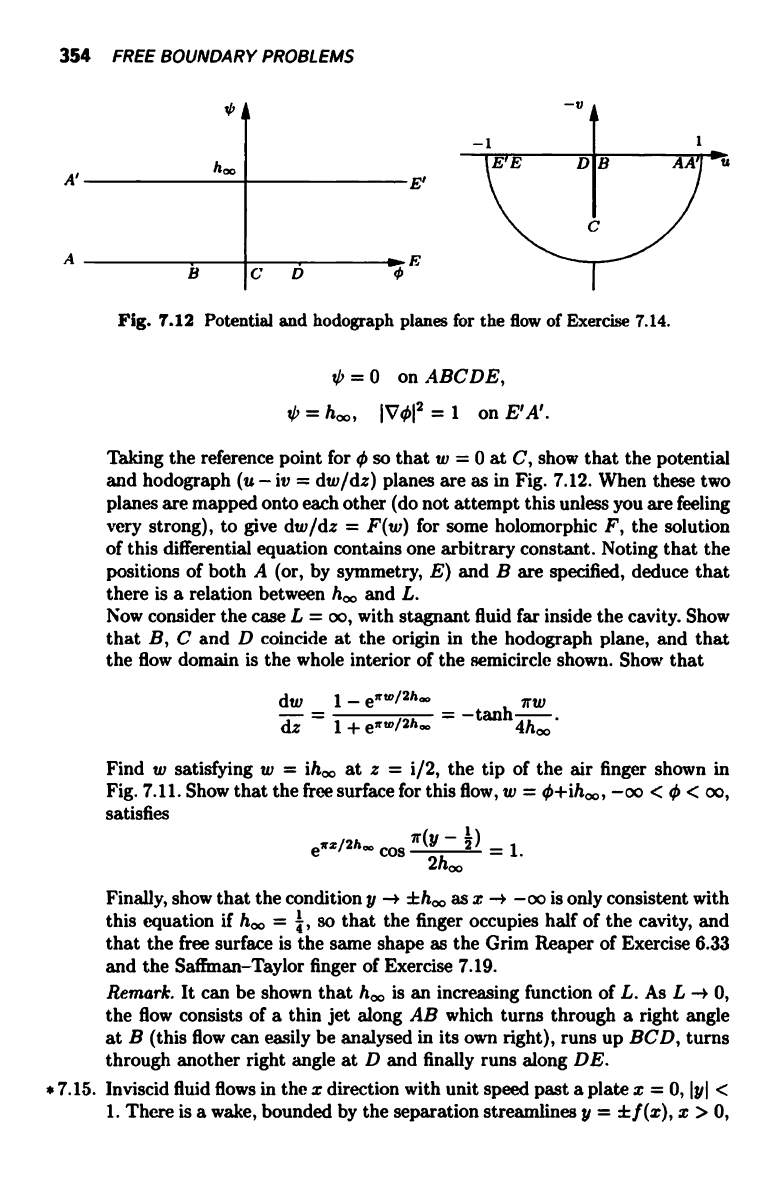
354 FREE BOUNDARY PROBLEMS

C D

Fig. 7.12 Potential and hodograph planes for the flow of Exercise 7.14.

0 = 0

on ABCDE,

t[i=ham,

IV012=1 onE'A'.

Taking the reference point for 0 so that w = 0 at C, show that the potential

and hodograph (u - iv = dw/dz) planes are as in Fig. 7.12. When these two

planes are mapped onto each other (do not attempt this unless you are feeling

very strong), to give dw/dz = F(w) for some holomorphic F, the solution

of this differential equation contains one arbitrary constant. Noting that the

positions of both A (or, by symmetry, E) and B are specified, deduce that

there is a relation between ho, and L.

Now consider the case L = oo, with stagnant fluid far inside the cavity. Show

that B, C and D coincide at the origin in the hodograph plane, and that

the flow domain is the whole interior of the semicircle shown. Show that

dw _

1 - eaw/2h

irw

dz 1+ eaw/2h -

-tank-.

Find w satisfying w = ih at z = i/2, the tip of the air finger shown in

Fig. 7.11. Show that the free surface for this flow, w = O+ih,,, -oo < 0 < oo,

satisfies

eR:/2h cos

x(y -

a) = 1.

Finally, show that the condition y -+ ±ho, as x - -oo is only consistent with

this equation if h = 4, so that the finger occupies half of the cavity, and

that the free surface is the same shape as the Grim Reaper of Exercise 6.33

and the Saffman-Taylor finger of Exercise 7.19.

Remark. It can be shown that hoo is an increasing function of L. As L -- 0,

the flow consists of a thin jet along AB which turns through a right angle

at B (this flow can easily be analysed in its own right), runs up BCD, turns

through another right angle at D and finally runs along DE.

s 7.15. Inviscid fluid flows in the x direction with unit speed past a plate x = 0, Jyi <

1. There is a wake, bounded by the separation streamlines y = ±1(x), x > 0,

EXERCISES 355

in which the pressure is constant. Show that the free boundary problem for

the separation streamline y = f (x), x > 0, is

V2q5=0 fory>0,

0-x at infinity,

with

and

y-(x,0) = 0

for x < 0

0, JV =1 ony= f(x),x>0.

Show that the flow region in the plane of w = O+iip can be taken to be Vi > 0,

with i = 0, ¢ < 0 being the upstream dividing streamline, 0 = 0, 0 < 0 < Oo

the plate and zG = 0, ¢o < 0 the free boundary. Show also that, in the plane

of W = log (dw/dz), these three curves are 3 W = 0, 0 > R W > -oo;

!` W = -ir/2, -oo < R W < 0; R W = 0, -ir/2 < a W < 0, respectively.

The Schwarz-Christoffel result can be used to show that the flow region in

the W plane can be related to that in the w plane (namely !3w > 0) uniquely

by the formula

w = ¢o cosech2 W,

where Oo = 0(0,1).

Show that this leads to the holomorphic differential equation

1---

Integrate this equation along the plate to obtain an equation for 00, and then

integrate along the free boundary to show that it is given parametrically by

z = i

o-w-./

Remark. The Schwarz-Christawful formula says that, if a; are the interior

angles of a dosed polygon, then the map

z - zo = ref (S), rc, zo complex constants,

where

df = n

real constants,

takes the real axis in the ( plane into a polygon with these interior angles,

with t;; mapping into the vertices of the polygon and the upper half of the S

plane mapping into the interior of the polygon. For fixed (;, different choices

of zo, argit and jrcl correspond to translation of the polygon, rotation of the

polygon, and expansion or contraction of the polygon with the ratio of its

sides fixed, respectively. Hence, given a target polygon with vertices z;, the

356

FREE BOUNDARY PROBLEMS

images of any three points (3, (2 and (3 can be chosen to be z1, z2 and z3,

respectively; however, the shape of the polygon is then uniquely determined

by (4, (3.... and the Riemann mapping theorem shows that z4, Z5.... do

indeed define (4, (5, etc. uniquely.

* 7.16. At time t = 0, a two-dimensional body y = f (x) - V t (where f (O) = 0,

d2 f /dx2 > 0 and f is even in x) impacts a half-space of inviscid liquid y < 0

from above. The free boundary problem for the velocity potential 0 is, in

the absence of gravity,

°20

= 0

in the liquid, with

0 -+ 0

as y -+ -oo,

with

8¢ 8q ey84

8¢

8y-8t+8x

8x'

° +8t=o

on the free boundary y = q(x, t), and

V+df04

dx 8x

on the wetted surface of the body.

Show that V can be taken equal to unity without loss of generality and that,

when the body is a wedge, with f = alxI, the problem is then invariant

under the transformations x' = eAx, y' = eay, t' = eat, q' = ear?, 4' = eao.

Deduce the existence of a similarity solution 0 = tO(X, Y), q(x, t) = tH(X),

x/t = X, y/t = Y, where

8X2 + 8Y2 =

0 in the liquid,

with

- tX

+YBY) + 2

t(8X )2

(87y)2)

= 0'

01 dH

BY =H - dX +BXd[

onY=H(X),and

8Y = -1 + a on on the wetted part of Y = aX - 1,

8.0

0 onX=0,Y<-1.

820

824

* 7.17. Suppose that the impacting body in Exercise 7.16 is y = e (f (x) - t), where

0< e<< 1 and t is not too large. Show that, if

= e +

, q = eqo +

EXERCISES 357

and terms quadratic in e are neglected, then the boundary conditions can

all be imposed on y = 0 in the form

8¢0

!°

8 °

°,

for jxj > d(t),

at -

8t ay

and

000 = -1 for lxi < d(t),

for some function d(t). Taking 00 = 0 on y = 0, {xi > d(t), use the methods

of §5.9 to show that

00 z+ z2-d2)

is the solution with the least singular behaviour at the `codimension-two'

free boundary lxi = ±d(t). Deduce that the pressure, which from Bernoulli's

equation is approximately -84o/et, is infinite at these points.

Remark. The evolution of d(t) can be predicted in terms of f (x) if it is

assumed that go(d(t) + 0, t) = f (d(t)) - t.

* 7.18. Suppose that p satisfies a Hele-Shaw free boundary problem in which V2p =

0, with p = 0 and Op/On = -v,, at the free boundary, denoted by t = w(x, y).

Show that

u(x, y, t) =

p(x, y, r) dr

satisfies the obstacle problem

V2u = 1

Show also that

with

n =0

on t = w.

0 )

9(z, t) =

\8x - i

4(x2 + y2))

is analytic, and that z = g(z, t) on the free boundary.

Remark 1. An analytic curve f (x, y) = 0 can be written as

= g(z), where

f ((z + g(z)) /2, (z - g(z))/2i) = 0. The function g is called the Schwarz

function of the curve and you may like to show that it satisfies g(g(z)) =

z, which is the consistency condition necessary when we replace one real

equation (f (x, y) = 0) by the complex equation # = g(z). Its determination

involves the solution of a Cauchy problem for its real or imaginary parts,

and so it is very likely to have singularities close to the curve.

Remark 2. For the Hele-Shaw problem above, the singularities of 9 within

the fluid are independent of t unless they coincide with those of p, because

8u/8t = p.

* 7.19. Consider Hele-Shaw flow in a parallel-sided channel -x < y < ir, -oo <

x < oo, in which the fluid is removed at a constant rate from x = +oc