Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

328

FREE BOUNDARY PROBLEMS

Sometimes these methods can point to impending disaster. Consider the one-

phase one-dimensional Stefan problem

02,u

for x < s(t),

(7.64)

8t - C7x2

with

u = 0, 8 = -dt at x = s(t), (7.65)

with supercooled initial data u(x,O) = uo(x) < 0, 0 < x < so, and assume that

8u/8x (0, t) = 0 for t > 0. Integration of the field equation, which is simply an

expression of global conservation of heat, gives

fos

(t)so

s(t) +

u(x, t) dx = so + 0 uo(x) dx. (7.66)

Now, if the solution exists for all t > 0, then there exists an s, such that

s(t) - s,,. > 0 and u(x, t) -+ 0 as t -* oo. Hence, if uo is so large and negar

tive that so + fo ° uo dx < 0, then we have a contradiction and so we have 'finite-

time blow-up', as in §6.6.5. The physical interpretation of this blow-up is that

if, in supercooled solidification, the latent beat released at the free boundary is

conducted away too quickly because u is too large and negative nearby, then the

steep temperature gradient at the front makes it move so fast (by the condition

Ou/8x = -ds/dt) that the gradient steepens even further and the free boundary

moves even faster. If the sign of u is reversed, so that the `active' phase is liquid

above the melting temperature, the free boundary moves in the other direction

and instability becomes stability. Moments such as (7.63) can be used to reveal

more information about blow-up when so + fo ° uo dx > 0 (see Exercise 7.9).146

7.3.3

Green's functions and integral equations

Although Green's functions cannot be used directly to solve free boundary prob-

lems, we can sometimes collapse information from the field equation onto the free

boundary and hence reduce the problem to a nonlinear integral equation, as in the

boundary integral method mentioned at the end of §5.5.2. As an example, consider

again the one-phase Stefan problem (7.64) and (7.65) for -oo < x < s(t), with

u(x, 0) = uo(x), assumed to behave suitably as x -+ -oo, and where no =- 0 in the

passive phase x > s(0). We define G(z, r - t; {) such that

- (aa2 + 8t

)

= 6(x - e)6(t - r) fort < r,

as usual. However, we make no specification about the boundary behaviour of G,

so that the Green's function for the whole line, written as

e-(s-t)'/4(*-t),

E(x - C, r - t) =

a(r - t)

'461n fact, the blow-up can occur even if the inequality is not satisfied, as long as uo is large

and negative near x = so.

WEAK AND VARIATIONAL METHODS 329

will suffice, as shown in [38]. Then the usual integration in the form

for

e(*)

82E 8E 82u

_ 8u

axa +

at)

- E (

8x2 at

}) dx dt

shows that

u(C, r) = U0 V) * E(C r) - f

ds(t)

E( - s(t), r - t) dt,

(7.67)

where * denotes convolution as usual. When the latent heat is zero the second

term is absent and this is simply (6.32). Now, as long as we are careful, we can

differentiate with respect to x and take the limit as t t 8(t), as in Exercise 7.10,

to obtain

1 ds

1 f r ds(t) (s(r) - s(t)

E (s(r) - s(t)

2 dr

8t' (u° * E)

l r _ t

, r - t) dt;

E=B(r)

(7.68)

taking the limit directly in (7.67) would yield a less tractable first-kind integral

equation. An iterative analysis may now be used to demonstrate existence and

uniqueness of the classical solution under appropriate conditions on Uo(x) [38].

Unfortunately, this technique does not readily generalise to multidimensional

free boundary problems, a matter to which we will return in §7.5. To make much

more progress with such problems, we must be less ambitious and consider gener-

alised rather than classical solutions, but, before we do this, we make one seemingly

trivial remark that is often overlooked. We can clearly transform any free bound-

ary problem to one in a fixed domain by a simple change of variable, such as

= x/s(t) or = x - s(t) for the one-dimensional Stefan problem. The price we

pay is that the field equation then involves coefficients that are global functions

of u and hence difficult to analyse. However, such transformations can be of great

computational advantage.

* 7.4 Weak and variational methods

Since classical free boundary problems are so difficult to analyse rigorously, it is

natural to try to ease the mathematical task by demanding a less stringent defini-

tion of the concept of solution. One possibility is to follow the ideas introduced in

§1.7 and to try to define a weak solution by multiplying the field equation by test

functions and integrating in such a way that the free boundary and the conditions

imposed on it are automatically incorporated into the integral formulation. Alter-

natively, we could try to generalise the variational approach described in §5.4 in

such a way that the free boundary conditions are automatically satisfied by the

minimisers.

In either case the philosophy is the same: we are seeking a formulation which

makes sense even in the presence of whatever discontinuities are inherent in the

free boundary conditions. The skill comes in writing down a formulation which has

good existence and uniqueness properties. Even if this formulation is too unwieldy

for as to have much hope of finding explicit formulae for generalised solutions, we

330 FREE BOUNDARY PROBLEMS

may hope that numerical discretisations can be devised that could be proved to

tend to the weak or variational solution when the appropriate step size decreases.

In Chapter 1 we have already seen the dangers of this philosophy. As we re-

minded ourselves in §1.7, when we used (1.22) to define weak solutions of hy-

perbolic equations, we found we had cast our net too widely and we needed extra

information before we could hope for uniqueness. In this chapter we are confronted

with a far wider range of problems, in which the field equation may be elliptic,

parabolic or hyperbolic, and for which all manner of free boundary conditions may

be prescribed. Hence, we have a major theoretical task ahead of us, and we begin

by making two general observations.

First, it will come as no surprise if we announce that the chances of finding a

generalised formulation of an arbitrary free boundary problem are very small,147

even though a surprising number of practically relevant problems are suitable

cases for treatment. Second, a crucial diagnostic feature is the `strength' of the

conditions at the free boundary, i.e. how many derivatives, if any, the solution may

be expected to have there. This especially concerns variational approaches because

we have a chance of formulating the problem as in §5.4 when, and only when, the

free boundary conditions are benign enough that only the highest derivatives in the

field equation are discontinuous. We saw there that the Euler-Lagrange equation is

of one order higher than that of the derivatives appearing in the Lagrangian; hence

a minimisation problem might still make sense and have the above-mentioned

degree of smoothness. We begin by considering this desirable situation.

7.4.1

Variational methods

The simplest situation of all arises when the free boundary emerges directly from

the kind of variational statement of the type used in §5.4. Suppose, for example,

that we wish to solve the vorticity problem (7.39). Replacing 10 by u and letting

u > 0 in the patch of vorticity, it is natural to consider

min f (

IVuI2

F(u))

dx, (7.69)

where

dF -

- f (u),

u > 0,

0, u < 0,

and the minimisation is taken over suitable test functions satisfying the required

conditions at fixed boundaries. To prove rigorously that this variational statement

has a unique solution is still hard work, even when, say, f is differentiable and

f (O) = 0. However, for our purposes, it is even more important that the varia-

tional statement achieves the objectives of any generalised solution, namely that

it includes all classical solutions. Hence we need to show that, if a free boundary

exists at which u = 0, then the minimiser has the correct behaviour there, with

8u/8n being continuous. We can see this by assuming that we can write the free

147We recall that we could only define weak solutions of hyperbolic equations when they were

in conservation form.

WEAK AND VARIATIONAL METHODS 331

boundary as S(x) = 0, with S > 0, where u > 0, and splitting (7.69) into contri-

butions from either side. When we change (u, S) to (u + du, S + 5S) we obtain, to

lowest order,

f bu (V 2u + f (u)) dx +

>0 u<0

r ([&u15=0+6u

5S=o_

+Js

1 5=0+

- IVul +

F(u)]

ds. (7.70)

s=o-

IoSI

taking the normal direction into the region where u > 0. The first two terms

vanish by (7.39). and F is continuous; hence, since bu and SS are independent, u

and Ou/On are continuous.

An even more subtle situation arises when we try the same idea on the obstacle

problem (7.40)-(7.42). Since the obstacle topography f does not in general satisfy

V f = 0, we cannot expect to get a solution by minimising the Dirichlet integral

Ioul2

dx over all small, smooth-enough perturbations. But it is natural, phys-

ically and mathematically, to consider the restricted or unilateral minimisation

problem

min

IVuI2 dx,

u_f

together with suitable conditions on u at the boundary of the membrane.

(7.71)

Again, it transpires that this minimisation can indeed yield an acceptable gen-

eralised solution to the obstacle free boundary problem just as long as u and Vu

are continuous at the free boundary. but now the proof requires quite a different

idea. In particular, it relies on the interesting identification between the following

three concepts.

1. The unilateral minimisation statement (7.71).

2. The so-called linear complementarity statement

V2u < 0, u > f, (V2u)(u - f) = 0. (7.72)

3. The so-called variational inequality over the fixed domain !1 containing both

the `contact' and 'non-contact' regions:

forally f, (7.73)

assuming that v satisfies suitable fixed boundary conditions.

It is difficult to establish the equivalence between the original problem (7.40)-

(7.42) and (7.71)-(7.73) rigorously, although (7.40)-(7.42) clearly implies the lin-

ear complementarity statement (7.72) (note that, when the membrane is in contact

with the obstacle, its linearised curvature O2u must be negative). To relate the

unilateral minimisation (7.71) and the variational inequality (7.73). note that, if

332 FREE BOUNDARY PROBLEMS

ul and u2 are candidates for (7.71), then so is eu1 +(1 -e)u2 for any a such that148

0 < e < 1. Hence the minimiser is such that

IVul2 dx

IV (eul + (1 - e)u2)

12 dx.

For small e, the right-hand side is equal to

I Vu212 dx + 2e j Vu2 0(u1 - u2) dx + 0(e2),

and so, with u2 = u and ul = v,

and the converse is obvious since IVU12 - IVvI2 = -2Vu 0(v - u) - IV(u - v)12.

Further details can be found in [17], where the advantages of each of the refor-

mulations (7.71)-(7.73) over the original problem (7.40)-(7.42) are also explained

in detail; in particular, the variational inequality is a good starting point for ex-

istence and uniqueness results, and the unilateral minimisation and the linear

complementarity formulation can have easy numerical implementations, as we will

see shortly.

This kind of approach only works if, firstly, the field equations are Euler-

Lagrange equations of a well-behaved functional and, secondly, the free boundary

conditions are sufficiently smooth. We have mentioned the latter fact several times

already and it is clear that this smoothness is needed to relate, say, (7.72) to

(7.73). Hence, if we are faced with a free boundary problem lacking the requisite

smoothness, it is tempting to try to transform it to one with better `regularity'.

A famous class of problems susceptible to such smoothing are the flows of a

liquid in a porous medium modelled by the steady versions of (7.14)-(7.16). For

these problems we can simply integrate with respect to the vertical independent

variable y (the Baiocchi transformation) and write the free boundary as y = h(x)

to give

p(x, y') dy' = u(x, y).

We restrict ourselves to stable situations where the saturated part of the porous

medium lies below the dry part. Then u >, 0 in the saturated region because p 3 0,

and, extending u and p to be zero in the dry region, a simple calculation gives

02u= 1, y<h,

with

u= =0 aty=h.

(7.74)

y > h, )

We thus have a free boundary problem which can be reformulated as a linear

complementarity problem similar to (7.72), or as the variational inequality

148Functional analysts

say that the minimisation is over a convex cone in a suitable function

space.

WEAK AND VARIATIONAL METHODS 333

fVu.V(v_u)dx)f(u_v)dx

(7 .75)

where the test functions v(x, y) are positive and satisfy appropriate fixed bound-

ary conditions, and Cl is the entire porous medium, including both saturated and

unsaturated regions.

An even more striking example of a smoothing transformation concerns the re-

lationship between the one-phase Stefan problem (7.64) and (7.65) and the oxygen

consumption problem (7.27). For the latter, we have seen that a physical argument

of mass balance at the interface suggests the free boundary conditions

c = TX

= 0

at x = s(t).

(7.76)

Now suppose oxygen is being consumed in 0 < x < s(t), with Oc/Ox = 0 at X. = 0

and s(0) = 1. The condition (7.76) gives enough smoothness for the complemen-

tarity formulation

OCa

\ a

cl- a+11=0, c'0,

Ot-Ox2'-1 (7.77)

to be shown to be equivalent to

//what

is called an evolution variational inequality

f (-1)(v- c)dx

(7.78)

for all positive v(x, t) satisfying appropriate conditions at x = 0, 1; with our par-

ticular initial and boundary data, we just need v = 0 at z = 1. Again, it is difficult

to prove the equivalence of (7.27), (7.77) and (7.78), although (7.77) and (7.78)

can be used to prove existence and uniqueness of weak solutions. But what is in-

teresting is that the Stefan problem (7.64) and (7.65) does not have the requisite

smoothness for a complementarity or variational formulation, yet it is apparently

intimately related to (7.27): when we formally set

c9c

= u (7.79)

in (7.27), we obtain

Ou 02u

(7.80)

Moreover, since

Ox2

09C

Occ_

=0 onx=s(t),

we see that is = 0 on x = s(t) and, since

02c ds

Ox2dt+OX Ot

0 onx=s(t),

we find

Oude

on x = s(t),

which is (7.64) and (7.65). Hence the Stefan problem is, formally, the time deriva-

tive of the oxygen consumption problem, and this applies in higher dimensions as

334

FREE BOUNDARY PROBLEMS

well. However, there is a catch here because we can only use (7.80) on the un-

constrained version of (7.27) in which the sign of c is not specified, rather than

the nicely-behaved constrained problem that can be written as (7.77) and (7.78).

In fact, we have indicated that, in two space dimensions, the Stefan problem can

behave very badly, and hence so can the unconstrained oxygen consumption prob-

lem. Yet the constrained oxygen consumption problem has perfectly good exis-

tence, uniqueness and continuous-dependence properties, at least as far as weak

solutions are concerned.

The complementarity approach can also be applied to some other models de-

scribed in the introduction, such as the dead core model mentioned in §5.11.3.

Equally, for the American option model a simple calculation shows that

at + 2QZsZ

02V

r (v

- s

J .

(7.81)

In financial terms, this is a natural requirement which says that the return on

a perfectly hedged option portfolio (the left-hand side) is never more than the

risk-free rate on the same portfolio (the right-hand side). If it is optimal to hold

the option, we have equality, but if we are in the exercise region it is suboptimal

to hold the option and so the return on the hedged portfolio is less than the

risk-free rate. This inequality can be used with the condition V >, max(E - S, 0)

and the fact that, whatever S, one or other of these inequalities is an equality, to

make a linear complementarity statement [47]. This in turn can be shown to imply

the smoothness condition that 8V/8S is continuous at the free boundary, i.e. the

classical free boundary conditions (7.20) hold (see Exercise 7.5).149

As our final example, we return to the smooth elastic contact problems men-

tioned in §7.1.3.2. Amazingly, they can all be formulated as variational inequalities

because, first, the elastic energy is minimised over the three-dimensional bulk of

the contacting solids, the Euler-Lagrange equations being (4.73) with 8/8t = 0;

second, the normal displacement and tractions are continuous (the tangential trac-

tion is zero) on the contact region, which to lowest order lies in a prescribed surface

S and is bounded by the one-dimensional free boundary r; third, no traction is

applied on S outside the constant region. The reason that this is a variational

inequality is now clear: on one side of r, conventional boundary conditions are

prescribed and, on the other side, the no-traction condition is the natural bound-

ary condition [12] for the elastic energy. Put crudely, the variational inequality

is clever enough to select that curve r on which the boundary conditions can

switch from contact conditions to natural boundary conditions with the requisite

smoothness, just as it does for the American option.

In summary, it is a red-letter day when a free boundary problem can be cast into

a variational formulation. Not only does this usually mean that rigorous statements

can be made about existence and uniqueness of a generalised solution, but the

numerical calculation of this solution can be relatively trivial. For example, for the

vector linear complementarity problem

1491n this respect the no-arbitrage condition acts rather like the second law of thermodynamics.

WEAK AND VARIATIONAL METHODS 335

u>0, Au>b, UT(Au-b)=0,

(7.82)

where positivity of a vector u means positivity of each component u;, we can put

r` a;juj I

(7.83)

uk+1 = 1

(ia -

L. L.

where A = (a;? ), and introduce a relaxation parameter w so that

uk+i = max (0, uk + w (uk+i - uj) )

gives an easily implemented updating for u; +1 in terms of 0, as described in

more detail in [13, 17, 47].

Hence, for example, option valuation can be carried

out quickly enough for the traders on Wall Street.

Despite all the success stories mentioned above, there remain many more free

boundary problems where there is inevitably insufficient smoothness for us to be

able to proceed variationally. Sometimes, however, we can have recourse to the

following method.

7.4.2 The enthalpy method

The enthalpy approach to the prototypical Stefan problem is similar in spirit to the

idea of weak solutions to hyperbolic equations. It is based on thinking of the free

boundary condition (7.4) as a Rankine-Hugoniot relation for a partial differential

equation in conservation form. Indeed, we recall that the one-dimensional heat

equation

02u

8t -

8x2

was derived from the integrated form of the conservation law

(h(u)) +

(_k±)

= 0,

(7.84)

where h = pcu is the heat content or enthalpy of the material. We now observe

that, if we set the melting temperature um to be zero, without loss of generality,

and write

h(u) _ pcu, u < 0 (solid),

pcu + pL,

u > 0 (liquid),

(7.85)

then the Rankine-Hugoniot condition for (7.84) is [-k au/Ox] dd = pL ds/dt, in

soli

accordance with (7.4). However, the other free boundary condition u = 0 is not

a Rankine-Hugoniot condition but rather the label of the temperature at which

the nonlinearity occurs; it indicates that the Stefan problem is really a limiting

nonlinear diffusion problem.

336 FREE BOUNDARY PROBLEMS

To make a mathematical theory out of these ideas, we begin by dealing just

with continuous functions, replacing (7.85) by u = F(h), where

h/pc,

h < 0,

F(h) =

0 < h < pL,

(7.86)

h/pc - L/c, pL < h,

and regarding (7.84) as an equation for F(h). Then we need to interpret (7.84)

properly, given that 8u/8x and 82u/8x2 do not exist at the free boundary. To

do this, we simply multiply (7.84), with u regarded as a function of h, by a test

function v which, in the simplest case of the Cauchy problem on -oo < x < oo,

vanishes for sufficiently large x and at t = T, and is infinitely differentiable. Hence

we can motivate the definition of a weak solution of this Stefan problem as a pair

of functions u and h satisfying (7.86) and such that

fT f3C

Bt dxdt = f_:hht_

0) dz

(7.87)

for all such

test

functions. The argument leading to (1.27) can then be used to

prove that any such u satisfies (7.3) and (7.4) (with u,,, = 0) at a phase boundary,

where 8u/8x is discontinuous. Moreover, this pair of functions (u, h) can be proved

to exist and to be unique (see [17)). The general idea of the proof is a by-product

of the most important practical implication of (7.87), which is the result that the

temporal discretisation

hn+l - hn

un+1= F (hn+1) +

(7.88)

which is easily implemented, converges to the unique weak solution. It is inter-

esting to note that the convergence of the analogous discretisation for hyperbolic

equations cannot be proved; this is because the weak solution is then not unique. In

fact, it is, in general, much more difficult to implement discretisations of the weak

formulation of hyperbolic conservation laws than it is for diffusive ones. We recall

that in the former case all the free boundary conditions are Rankine-Hugoniot

conditions for conservation laws, whereas in the Stefan problem the condition

[kVu n);oludid = -pLvn is triggered by the discontinuity in the enthalpy. The

rapid transition across, say, a gasdynamic shock wave can easily generate spurious

high-frequency oscillations in the solution of the discretised weak formulation, and

these oscillations can propagate as waves throughout the flow more easily than

can the oscillations generated at a phase boundary by the solution of (7.88).

The algorithm (7.88) is known as the enthalpy method for the Stefan problem.

It is a simple matter to generalise the method to more than one space dimension,

even when it comes to proving existence and uniqueness of the weak solution; this

is in contrast to the classical solution whose existence is hard to prove in more

than one dimension.

We see the most dramatic implication of the enthalpy method when we enquire

about the relationship between classical and weak solutions of the Stefan problems.

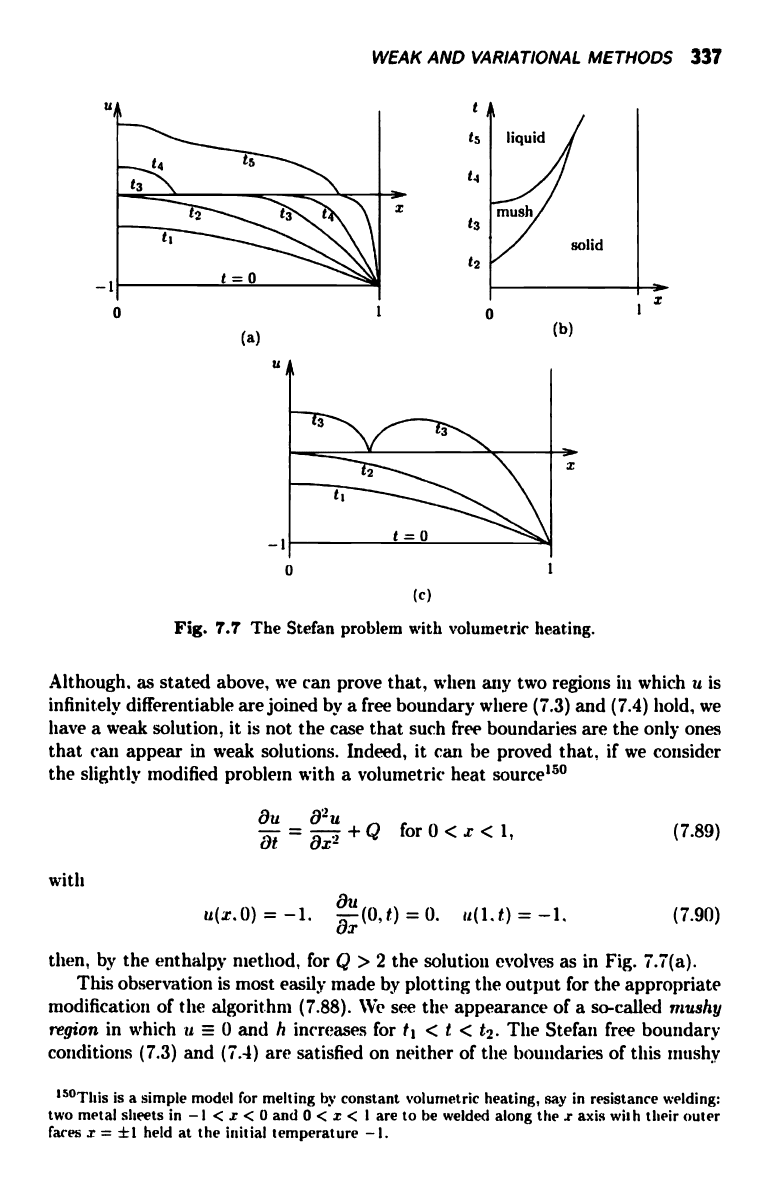
WEAK AND VARIATIONAL METHODS 337

(a)

(c)

(b)

Fig. 7.7 The Stefan problem with volumetric heating.

Although. as stated above, we can prove that, when any two regions in which u is

infinitely differentiable are joined by a free boundary where (7.3) and (7.4) hold, we

have a weak solution, it is not the case that such free boundaries are the only ones

that can appear in weak solutions. Indeed, it can be proved that, if we consider

the slightly modified problem with a volumetric heat sourcetso

5(32 U

T+Q

for0<.c<1,

8x'

with

(7.89)

u(x,0) = -1. Ou(0't)=0.

(7.90)

then, by the enthalpy method, for Q > 2 the solution evolves as in Fig. 7.7(a).

This observation is most easily made by plotting the output for the appropriate

modification of the algorithm (7.88). We see the appearance of a so-called mushy

region in which it = 0 and h increases for tt < t < N. The Stefan free boundary

conditions (7.3) and (7.4) are satisfied on neither of the boundaries of this mushy

'50This is

a simple model for melting by constant volumetric heating, say in resistance welding:

two metal sheets in - l < x < 0 and 0 < x < I are to be welded along the r axis with

their outer

faces r = ti held at the initial temperature -l.