Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

308

FREE BOUNDARY PROBLEMS

t suction or injection

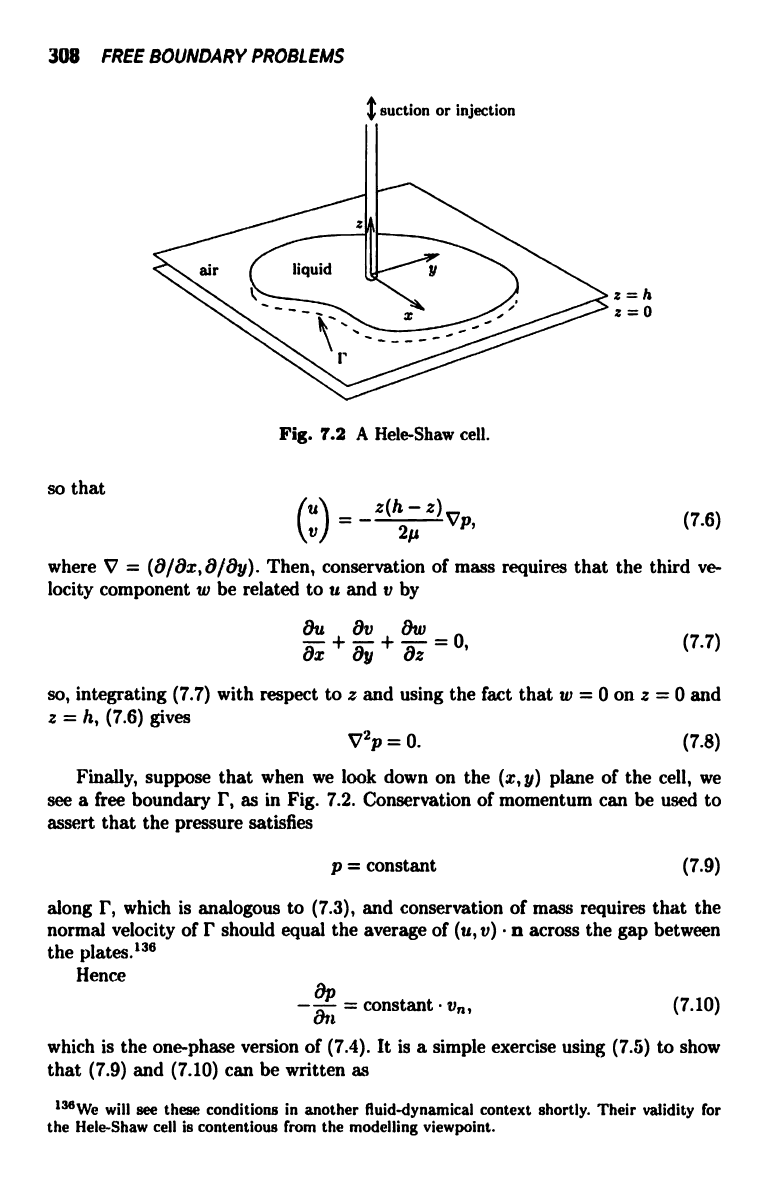
Fig. 7.2 A Hele-Shaw cell.

so that

z(h - z)

VP,

where V = (8/8x, 8/8y). Then, conservation of mass requires that the third ve-

locity component w be related to u and v by

8v 8w

Y.-

8y + T.

_ 0,

so, integrating (7.7) with respect to z and using the fact that w = 0 on z = 0 and

z = h, (7.6) gives

V2p=0.

(7.8)

Finally, suppose that when we look down on the (x, y) plane of the cell, we

see a free boundary r, as in Fig. 7.2. Conservation of momentum can be used to

assert that the pressure satisfies

p = constant (7.9)

along r, which is analogous to (7.3), and conservation of mass requires that the

normal velocity of r should equal the average of (u, v) n across the gap between

the plates.136

Hence

- = constant v,,,

(7.10)

which is the one-phase version of (7.4). It is a simple exercise using (7.5) to show

that (7.9) and (7.10) can be written as

tsWe will see these conditions in another fluid-dynamical context shortly. Their validity for

the Hele-Shaw cell is contentious from the modelling viewpoint.

INTRODUCTION AND MODELS 309

IVPI2 = 0,

(7.11)

with a suitable resealing of p.

One of the great virtues of this model is that it has a simple generalisation which

is one of the easiest free boundary problems to visualise: simply squeeze together

two transparent sheets with a drop of viscous liquid, such as shampoo or treacle,

sandwiched between them, because setting w = 8h/8t on z = h merely converts

(7.8) into a Poisson equation with a term proportional to Oh/8t on the right-

hand side. However, the Hele-Shaw problem also models the important process

of electrochemical machining, where a metal `workpiece' is to be eaten away into

a desired shape by being immersed in an electrolyte. Then, if 0 is the electric

potential in the relatively poorly conducting electrolyte, and we are away from the

thin layers of high charge density near the workpiece, the argument in §5.1.2 gives

V20

= 0, (7.12)

with, say, 0 = 0 on the workpiece. Moreover, it is observed that dissolution at the

workpiece occurs at a rate proportional to the local electric field, so that, again,

= constant v,,; (7.13)

the sign of 0 in the problem changes if deposition occurs, as in the process of

electroforming.

Almost the same model arises in porous medium flow in the absence of gravity.

Suppose the flow is modelled as in §5.1.4.4 but that, as in Fig. 7.3, the porous

medium contains a free boundary 1' separating adjacent regions, in one of which

the pores are full of water, so that the medium there is `saturated', and in the

other the pores are completely dry (partial saturation always occurs in reality,

but often only over quite thin regions). We again have Laplace's equation for the

pressure in the saturated region and the arguments leading to the Hele-Shaw free

boundary conditions can be repeated. If, on the other hand, gravity is important,

so that Darcy's law is

v = -V (p + y)

(7.14)

in non-dimensional variables with y vertical, then, in incompressible flow,

Fig. 7.3 Porous medium flow.

310

FREE BOUNDARY PROBLEMS

(7.15)

The mass conservation condition at the free boundary f = 0, where p vanishes,

becomes

8 - Vpf =Of

(see Fig. 7.3).137 Since p = 0, we can, as in (7.11), write this condition as

etIVP12=Oy

(7.16)

A further generalisation would be to suppose that the free boundary separates

two immiscible fluids with different viscosities µ1,2, such as oil and water. Then, in

the absence of any interfacial forces, such as capillarity, the momentum and mass

balances at 1' yield the so-called Muskat problem, whose free boundary conditions

in suitable dimensional variables are

OPwater

_18poil

Pwater = poll,

Awater

= Roil

= -vn

in the absence of gravity. The Hele-Shaw model can then be retrieved as a one-

phase limit (see Exercise 7.2).

7.1.2 Other free boundary problems in diffusion

An interesting problem in finance describes the valuation of a particular kind of

option called an American put option. This differs from the 'European' call option

described in §6.1.2 in two ways. The first is that the holder has the right to sell the

asset for a specified amount E, instead of buying it. The second is that the right to

sell can be exercised at any time up to the pre-assigned expiry date, t = T, rather

than only at t = T. This introduces the idea of an 'optimal exercise price' into the

modelling and converts what was a conventional parabolic equation model into

a free boundary problem in which the free boundary is the graph of the optimal

exercise price as a function of time t.

Suppose we have the flexibility inherent in American options. To accord with

the absence of arbitrage, the option value must be at least equal to the proceeds

of exercising it, since exercise can take place at any time. We can extend the

discussion after (6.10) to note that, if S < E, then the net result of buying the

option, at a cost of -V, and exercising it immediately to yield E - S, is E - S - V.

Hence, in the absence of 'free lunches', for 0 < t < T, V >, E - S, and a similar

argument shows that we must also have V > 0. Furthermore, if S falls to zero, then

it remains there, and the holder should obviously exercise the option immediately

in order to gain from the interest on the proceeds. There must therefore be a range

of values 0 < S < S' (t) in which the option should be exercised, so in this range

137The configuration in which the porous medium is a rectangle separating two reservoirs of

water of different prescribed depths is now so famous that it is referred to as the dam problem.

INTRODUCTION AND MODELS 311

its value is E - S, while for S' (t) < S < oc the Black-Scholes equation still holds.

We therefore seek solutions of

8t +

2a2S2

6S2 =r [ V - S

5S I

for S'(t) < S < oc, (7.17)

where V -* 0 as S -; oo and, if the option is still unexercised at t = T,

V(S,T) = max(E - S,0).

(7.18)

As explained above, we also expect that

V(S,t)3max(E-S,0) for0<t<T,

(7.19)

with equality only holding in the region 0 < S < S*(t), where the option is

exercised. This simple-minded argument does not give a free boundary problem

for V in the style of §7.1.1. However, further consideration of the optimal exercise

strategy (see Exercise 7.4) reveals that 1' satisfies the free boundary conditions

V=E-S, as1 atS=S'(t), (7.20)

these two free boundary conditions being analogous to specifying the melting tem-

perature and balancing the energy at the free boundary of a Stefan problem.

The question of determining what extra information should be assigned at the

free boundary is also illustrated by the modelling of flames as combustion problems,

usually in gases, in which the important chemical reactions only occur in the flame

sheet. In many cases of practical interest the thickness of flame sheets is much less

than the typical dimensions of the environment in which the flame exists, and

hence a free boundary model might be appropriate. Unfortunately, combustion

modelling is such a complicated subject that we can only mention two simple free

boundary approaches that can be used to predict flames. The relevance of each

approach depends crucially on whether the reactants are provided 'ready-mixed'

and capable of being ignited, say by a spark, or whether diffusional mass transfer

has to occur in order to create the correct `stoichiometric' mixture.

The former case leads to what is called a premixed flame, and in theory it should

be modelled by coupled equations for the temperature T and reactant concentra-

tion c, as in §6.7.2. The key modelling assumption that leads to a free boundary

problem is that the dimensionless rate of reaction is, as in §§5.11.1 and 6.6.1, of

the form Ace-EST, where A is constant and the dimensionless `activation energy'

E is large. This implies that the reaction term is negligible except where the tem-

perature is near its highest value, say To, which is now an unknown of the model.

It can then be expected that the reaction is confined to a thin region where T

is close to To but where c is still appreciable. Assuming purely conductive heat

transfer (as, say, for combustion in a solid such as a cigarette), in one dimension

we are led to the model

OT 02T

= k

8-2

(7.21)

312

FREE BOUNDARY PROBLEMS

in the region ahead of the flame, say x > s(t), with

T=To

(7.22)

at and behind the flame, x < s(t). We now see another one-phase free boundary

problem beginning to emerge in x > s(t), but, at the moment, we know neither

To nor OT/8x as x l s(t).

We can make some further progress by assuming that the mass consumption

is proportional to the rate of reaction, so that the reaction zone near the flame is

modelled by

8 2c

EST

= k- + Ace D ace-'/ (7.23)

8x2

8t=

where a is a constant analogous to A. As discussed in §6.7.2, such parabolic systems

are not easy and here we make the further assumption that the reaction front is

a slow travelling wave solution of (7.23) in which T is close to To. Thus, when we

neglect 0/8t and notice that

c-+0, T-+To

behind the flame, we can add and integrate to find that

akT + ADc = akTo.

(7.24)

(7.25)

Finally, approximating a-E/T by

e-E/ToeE(T_To)/To

, as in §6.6.1, we can integrate

02T

a _EITo

E(T-To)/To

Ox2 +

(To - T)e - 0

once, and use (7.24) again and the fact that T - To is relatively large and negative

ahead of the flame, to give

OT I

_ = 2a Toe-E/27°. (7.26)

8x =_a(e)

This gives the second Stefan condition to go with (7.22), but To is still undeter-

mined; we will return to this question in §7.5.1.1.

A quite different situation occurs when the ambient combustible material is

not supplied in a premixed form. Suppose instead that there are just two reacting

components, for example fuel at concentration cl and oxygen at concentration c2i

and that they only react where they diffuse into each other. For `fast' reactions,

the concentration of oxygen is negligible on the `fuel side' of the flame, and vice

versa, in which case we simply have to solve diffusion equations for c{ on either side

of the flame, at which cl = c2 = 0. Also, since all the chemical reaction takes place

at the free boundary, a `stoichiometric' condition holds there. This is jargon for

the fact that, because chemicals react in fixed ratios (for example, two hydrogen

molecules and one oxygen molecule combine to create water), the rates at which

INTRODUCTION AND MODELS 313

chemicals are used up at a flame are proportional to each other. Hence there is a

linear relationship between the two mass flows,

On = -" On '

where A is a constant. This is a model for so-called diffusion flames, and contrasts

with the Muskat problem.

Flame modelling in gases is often further complicated by the presence of con-

vection, which is strongly coupled to the equations of heat and mass diffusion, and

can lead to phenomena such as quenching or, with compressibility important, to

detonation or deflagration, as discussed in §2.5.3.

Less dramatic diffusion processes may lead to free boundary problems which

are so `mild' that the free boundary conditions may be implicit in the modelling

statement. In fact, we have already encountered such a situation with models lead-

ing to the porous medium equation (6.72), Op/Ot = V (p"Vp), in the derivation

of which we tacitly assumed that the pressure p (or the film thickness h if that is

the dependent variable) is positive. However, it is easy to imagine that the `active'

region in which p > 0 abuts an inert one in which p = 0. Now p = 0 is a solution

of (6.72), so this prompts the question `suppose we have an initial value problem

in which the data vanishes in some region and is strictly positive elsewhere; does

it make sense to try to solve the equation as it stands for t > 0 and hope the free

boundary separating the active and inert regions comes out in the wash?' Strictly

speaking, the mathematical answer to this question is no, unless the derivatives

of p are such as to make V (p' V p) vanish at the free boundary; only in such a

case could the left- and right-hand sides of (6.72) be equal there. Everything boils

down to the smoothness of the solution and we will have to focus on this in our

later discussion of the porous medium equation.

Another interesting situation occurs in the oxygen consumption problem in

which oxygen is removed from a biological tissue by chemical action at a rate

which is approximately independent of the amount of oxygen remaining, just as

long as the latter is positive. A very simple one-dimensional model for the oxygen

concentration c is

Oc 02c

8t 8x2

-1, (7.27)

which at first sight seems to be a simple linear case of the reaction-diffusion

problems studied in §6.6. However, the simple solution c(x, t) = constant - t shows

that we must take care to enforce the physical requirement that c >, 0. Thus,

in line with some earlier models in this chapter, we could propose a one-phase

free boundary model in which regions where c > 0 adjoin regions where c = 0,

and (7.27) only holds in the former. The two free boundary conditions would be

c = 0 and, by conservation of mass, Oc/8x = 0. However, an alternative approach,

in the spirit of Chapter 6, would be to replace the right-hand side of (7.27) by

-H(c), where

H(c) _

c > 0,

0, c<0,

314

FREE BOUNDARY PROBLEMS

the Heaviside function, is clearly a nonlinear function of c.138 The relationship

between these approaches thus leads to yet another mathematical question akin to

those raised in connection with the porous medium equation and with the model

for American options, and we will see that its answer lies in some interesting

theories of weak solutions for parabolic equations.

7.1.3

Some other problems from mechanics

In Chapter 2 we have already encountered one of the most intensively studied free

boundary problems, namely that of shock waves in compressible fluids. We recall

that the most difficult aspect of our discussion there concerned the question of

uniqueness, for either the classical formulation or the weak formulation. In both

cases we found that, in order to obtain a unique physically acceptable solution, we

needed to append an extra restriction to the Rankine-Hugoniot relations. This was

despite the fact that these relations apparently already contain an extra equation

over and above those that would be needed for a Cauchy problem with a smooth

solution on a prescribed domain. For example, for the simple model

8u au

(7 28)

+ u

with Cauchy data u(x, 0) = uo(x), a count of the number of pieces of information

would not lead us to expect to be given any data other than the Rankine-Hugoniot

condition in order to be able to determine the unknown position, x = 8(t), of

a shock. However, our discussion at the end of §1.7 tells us that the Rankine-

Hugoniot condition allows us too much freedom and that a further restriction is

needed to obtain a unique physically acceptable solution.

Bearing this idea in mind, we now list some further free boundary problems in

mechanics.

7.1.3.1

Fluid dynamics

A venerable source of free boundary problems is the mechanics of continua that

have a `free surface', which in mechanics often means a 'stress-free' surface. The

simplest case occurs in irrotational inviscid fluid dynamics which provides a model

for, say, water in motion beneath an atmosphere which exerts no stress other

than a constant pressure. Then, in the absence of surface tension, a momentum

balance demands that the water pressure p is equal to atmospheric pressure. Now,

as will be shown in Chapter 9, it is a simple deduction from the time-dependent

generalisation of (2.5) and (2.6) to show that, when the density p is constant, p is

given everywhere in the water by Bernoulli's equation

P +

+ gy + 8 = constant,

(7.29)

where y is the vertical coordinate and 0 is the velocity potential, which satisfies

Laplace's equation. Hence, if we denote the water surface by y = 77(x, t), then, in

a two-dimensional problem,

13SThis is a special case of the problem of `dead cores' in more general chemical reactions in

which the right-hand side of (7.27) is proportional to cp, as mentioned at the end of §5.11.3.

INTRODUCTION AND MODELS 315

i§F

IV0I2 + 99 +

= constant

on y = il. (7.30)

Also, we know that, whether or not y = sl is stress free, no fluid particles can

cross this surface, i.e.

a4)

= vn,

(7.31)

where, as usual, vn is the normal velocity to the surface. Using (7.5), we have our

second free boundary condition,

at +

ax ax

on y = r1. (7.32)

It is possible to non-dimensionalise the variables, so that (7.30) becomes

+ 2 Io012 + Fq = constant,

(7.33)

where F is a dimensionless number called the

number; the larger the value

of F, the larger is the effect of fluid inertia relative to gravity.

We can already see an opportunity for `technology transfer' from gas dynamics.

For, suppose we replace the atmosphere by a second active inviscid irrotational

fluid, with a constant density p' 0 p, could we not regard the free surface as a

`shock' and derive (7.30)-(7.32) directly? After all, the fluid dynamics equations

were originally conservation statements, although we have rather lost sight of this

when we transformed to the variable 0. Anyway, the answer to our question is in

the affirmative because the Rankine-Hugoniot condition for the mass conservation

equation, namely

at + V (pu) = 0,

(7.34)

is [p] vn = [pu n), which leads to (7.32) when p' = 0 and u = p.0.139

The simplest class of such inviscid free surface flows and, indeed, the only class

that is at all tractable as far as explicit solutions are concerned, occurs when

139For the momentum conservation equation in three dimensions, we must regrettably write the

conservation law in suffix notation as

(p&v + pu,u,) = 0,

(7.35)

where u = (u;) and 6,, is the identity matrix. We then find that

[pn + p(u n)uj = [pu]v,,,

which leads to (7.33) when g = 0. Note also that, when p # p' and neither is zero, then (7.32)

and (7.35) also admit the possibility that

[p]=0,

which is what we called a contact discontinuity on p.59, and which is illustrated by (7.37).

316

FREE BOUNDARY PROBLEMS

the flow is steady and two-dimensional, and F is infinite in (7.33). Then the free

boundary conditions for Laplace's equation become

= 0,

tool = 1, (7.36)

without loss of generality, and we have what is called a Helmholtz flow. 110

An interesting complication is introduced into these kinds of inviscid flows

when, in a two-phase problem, we permit relative tangential motion to occur across

the free boundary, even across a free boundary where there is no density discon-

tinuity. Then we have what is called a vortex sheet, at which the free boundary

conditions for the velocity potential ¢i on either side are

t t

2 2 + &

= 1 X0

I X0

021

+ cons

an ,

¢11 +

(

. )

which is conservation of normal momentum, and

1901

1902

= v"

(7.38)

8n '

which is conservation of mass.

Further possibilities arise when we consider rotational inviscid flows. In steady

two-dimensional situations we have seen in §5.11.1 that the stream function b(x, y)

satisfies

-V2tb = f(,p),

(7.39)

where f (,t') is the vorticity and is usually an unknown function. However, there is

often experimental evidence that the vorticity is localised in a patch and, if this is

the case, we could take f to be a function with compact support. The question then

arises as to what free boundary conditions should be imposed at the boundary of

the patch.141 As for free surface flows, no particles can cross the free boundary r,

which is thus a level curve of 0 in steady flow, with t' continuous at r. Also, since

the pressure must be continuous to ensure momentum conservation, the Bernoulli

condition requires that the tangential velocity 80/8n must be continuous at r.142

The list of problems of this type is long enough, even without introducing

the effects of viscosity, which leads to considerable algebraic complications (see

Exercise 7.6). Hence our final examples come from solid mechanics.

7.1.3.2 Solid mechanics

Stress-free boundaries are also ubiquitous in solid mechanics, but fortunately many

elastic bodies only undergo such small displacements that their free surfaces may

be regarded as being more or less in prescribed positions. This enables previously

140These free boundary conditions also arise in certain very simple models of flame propaga-

tion (7].

141 Precisely the same problem arises when we model the magnetic confinement of a plasma (an

ionised gas) in a long tube.

142Again, we will have to wait until Chapter 9 to explain the Bernoulli condition.

INTRODUCTION AND MODELS 317

contact set

rigid obstacle z = f (x. y)

Fig. 7.4 Obstacle problem for a membrane.

mentioned theories of linear elasticity to be used, but there is one situation where

nonlinearity cannot be avoided, even though the displacements are small. This

happens whenever two elastic bodies come into contact because, even though the

small transverse displacements on a smooth contact region can be regarded as

part of the data for the problem, the perimeter of the contact region is an un-

known free boundary. We have already encountered such problems in §§5.1.6.2

and 5.9.5, but, because we only considered two-dimensional configurations there,

the contact perimeter consisted of discrete points. We showed that their location

could be determined by applying appropriate singularity conditions in their vicin-

ity and equations such as (5.151) reveal the nonlinearity of the problem. Similar

contact problems in three-dimensional elasticity reveal the same dimension deficit,

in that the lowest-order problem is to find the one-dimensional perimeter of a

two-dimensional contact set. We will return to this topic of 'codimension-two' free

boundaries at the end of the chapter, but there is one special case that is rela-

tively easy to model yet leads to a conventional `codimension-one' free boundary

problem. This is when one of the bodies is rigid and smootht43 and the other thin

and extensible enough to be modelled as a smooth membrane, as in Fig. 7.4.

We then have what is called an obstacle problem, which is simple to state if we

assume that the membrane is stretched, with a fixed perimeter r o and only has a

small deflection when it comes into contact with the rigid obstacle z = f (x, y). As

in §5.1.4.2, in equilibrium the transverse displacement u(z, y) satisfies

V2u=0

(7.40)

wherever the membrane is not in contact, i.e. when u > f, but otherwise u = f

and we have a free boundary r to the contact region. Although it is obvious that

u = f on r, we again have our familiar question of what extra information needs

to be imposed there. This situation is simple enough that we can see at once

that equilibrium can only be maintained in the vicinity of r if the tension T is

continuous and the force is the same as we approach r from either side; this

is the same as carrying out the balance that led to (7.30), with the free boundary

being a curve rather than a surface. Hence our free boundary conditions are simply

1431f the contacting bodies are rough, then the interesting problem arises of determining another

free boundary, namely that between the regions of sliding contact and the regions of adhesion.