Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations
Подождите немного. Документ загружается.


338
FREE BOUNDARY PROBLEMS
region; only after the mushy region has vanished (Fig. 7.7(b)) does such a classical
Stefan free boundary emerge, for example at t = t5.
Additionally, it can be shown that, if we were to insist that the only free bound-
ary in the problem was to be one at which the classical Stefan conditions (7.3)
and (7.4) were satisfied, then the solution would evolve quite differently, and, as in
Fig. 7.7(c), it would involve a superheated region in which the solid temperature
exceeds the melting temperature. We recall that our stability argument for the
case of zero specific heat in §7.2.3 suggested that such superheating yields a free
boundary that is unstable to small disturbances in two dimensions.
The physical interpretation of Fig. 7.7(a), with its prediction of coexisting
liquid and solid phases, demands much more detailed physical scrutiny than we
can give here, but it is likely that Fig. 7.7(a) is more realistic than Fig. 7.7(c) in
many practical situations. What has happened mathematically is that the enthalpy
formulation has legislated against superheating (as it would against supercooling)
because of the nature of the function h(u) in (7.85). We remember that at no
point in our classical formulation did we prohibit superheating or supercooling
and the weak formulation is a valuable reminder that these constraints are just as
important as they were in the oxygen consumption problem.
Although the Stefan model is one of the commonest free boundary problems
where a weak formulation is available, the idea can be tried on any problem in
divergence form. For example, when applied to the one-dimensional porous medium
equation (6.72), it gives
u=0,
un-18
= d
(7.91)
as free boundary conditions for a weak solution, the second of which can sometimes
be interpreted as conservation of mass at the free boundary. However, we must
remind the reader of the fragility of the situation. It only needs, say, the melting
temperature or latent heat to be a function of position for the weak formulation
of the Stefan problem to cease to be available.
Free boundary problems are one area of partial differential equations theory
where rigorous existence and uniqueness proofs and justifiable numerical algo-
rithms far outnumber the techniques available for finding explicit solutions. Some
of the few techniques that are available are described below.
7.5
Explicit solutions
Only two of the techniques described in Chapters 4-6 can be used with confidence
to find explicit solutions of free boundary problems. They are, firstly, the use of
similarity variables which, we recall, includes travelling waves, and, secondly, the
use of complex variables if the field equation happens to be Laplace's equation or,
perhaps, the biharmonic equation. The use of complex variables leads to the idea
of conformal invariance and thus can be regarded as a special case of a similarity
method, but the associated techniques are distinctive enough to merit separate
discussion.

EXPLICIT SOLUTIONS 339
7.5.1 Similarity solutions
All the remarks about similarity and group invariance made in §6.5 apply to any
differential equation, with a free boundary or otherwise. However, success always
relies on identifying the relevant group, so we will simply list some informative
examples.
7.5.1.1 Travelling waves: similarity variable x - Vt
When the independent variables x and t do not appear explicitly in the field
equations we can always seek solutions that depend just on x -1't for some con-
stant V and, for certain one-dimensional free boundary problems, this allows the
free boundary to be at x = Vt. For example, the one-phase Stefan problem (7.64)
and (7.65), in which water occupies the region x < I't, has a solution u = F(x-1't)
as long as
where, since the ice in
Hence
ddseF+1'd
=0,
x > 1't has temperature u = 0,
F(0)=0, aF(0)_-1.
(7.92)
(7.93)
u(x, t) _ -1 + e-t
(=_t
(7.94)
and we see that, if V > 0. and we have what we regarded in §7.3.2 as a stable
situation with the water temperature above zero, then u -4 +oo as x -1't - -oo.
However, if 1' < 0, then u -4 -1 as x - Vt -> -oo and we will see the significance
of this limiting value shortly.
Travelling wave solutions can be sought for many of the other models described
in §7.1. At one extreme, the Rankine-Hugoniot equations themselves provide very
simple travelling wave solutions for shocks in hyperbolic conservation laws, while
the problem for travelling two-dimensional surface gravity waves is still a chal-
lenging task for numerical and mathematical analysts, unless the wave slope is
small.
In combustion theory. our indeterminacy after (7.26) can be resolved by mod-
elling flames travelling into a premixed environment with (7.21), (7.22) and (7.26),
and, after making the key assumption that we can neglect the reaction ahead of
the flame. seeking a travelling wave. We find the profiles
T(x,t) = T.t + (To - T4)e-t
c.(x.I) = CO (I
(7.95)
for the temperature and concentration, respectively, in x > s(t) = 1'I. where
T., and co are, respectively, the values of the temperature and concentration far
ahead of the flame. The compatibility condition (7.25), when applied to (7.95)
for small positive values of r - Vt. shows that To is given by Te) - T.t = .-loo/n.
which has the simple physical interpretation that the rise in temperature is that
achieved by the complete reaction. Finally, (7.26) gives the flame velocity as V _
2a/DE(kTo/(Tu - T.t ))e-Fr2T,

340
FREE BOUNDARY PROBLEMS
Unfortunately, this approximate solution loses self-consistency at large dis-
tances ahead of the flame because the reaction terms in (7.23), although small,
dominate the derivatives unless TA is absolute zero. This is the so-called `cold
boundary difficulty'. The contradiction can be explained away by the fact that, in
real life, the model only applies for finite times and in bounded regions. Indeed,
if we apply the condition T = TA at a finite, but suitably large, distance ahead
of the flame, (7.95) gives a good approximation to T and 8T/8x except, possibly,
near this cold boundary.
There is a famous travelling wave solution of the equations (2.3) and (2.4) of
unsteady one-dimensional gas dynamics, where we recall that the free boundary
conditions at a shock moving with speed V are given by (2.49). We examine the
flow produced by instantaneously pushing a piston with speed Vp into a tube
containing gas at rest at pressure po and density po. By seeking a solution in
which u, p and p are all constants for Vpt < x < V t, it is relatively easy to see
that the free boundary velocity is
ry + 1
FV2
16 42
V4 CVp+
+ry+1)2
where a2 = rypo/po (see Exercise 7.12). Similarity solutions also exist in multi-
dimensional steady flow past wedges and cones, where non-uniqueness can occur
(non-existence of the solution is also possible).
7.5.1.2
Other similarity variables
With a particular class of initial and boundary conditions, the Stefan problem
provides an informative reduction of a partial differential equation free boundary
problem to one for an ordinary differential equation.151 It is easy to see that,
as long as the initial temperatures on either side of x = s(t) are constant, with
one phase in s(t) < x < oo and the other in -oo < z < s(t), the initial and free
boundary conditions are all invariant under the transformation x' = eax, t' = e2at,
s' = eaa, u' = u. Hence, as in (6.44), we can set
s(t) = at1"2,
n = xt-1
"2
and u = U(rl), (7.96)
where a is a constant, to give
d
2*
(7.97)
In the one-phase case with water in -oo < z < s(t), and u(x, 0) = uo = constant
and s(O) = 0, we find
U(a)=O, d
(a) = - - 2,
and hence, from (7.97),
Isi We recall that a similar group invariance argument was used to find some free boundaries
for the porous medium equation in §6.6.
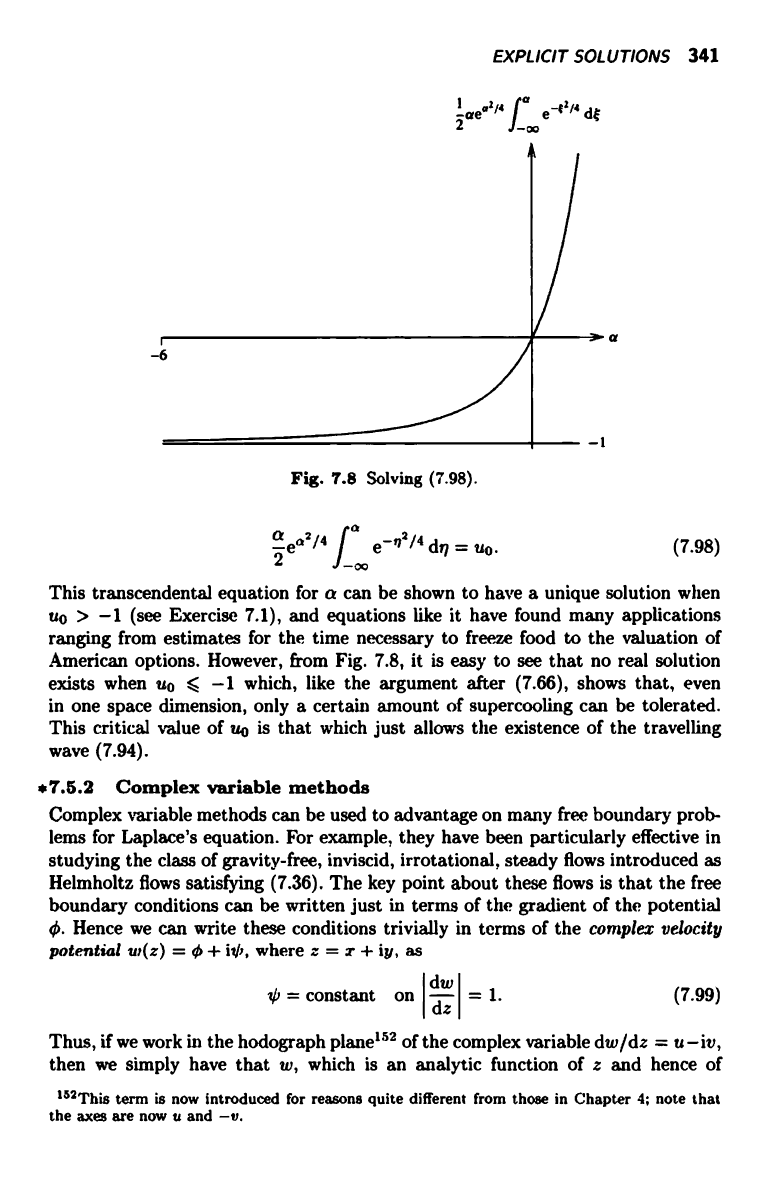
EXPLICIT SOLUTIONS 341
2aea=Ia ra a-t2/4 dt
J o0
Fig. 7.8 Solving (7.98).
ea214
I
e-+1214 dr1
= uo.
a
0
This transcendental equation for a can be shown to have a unique solution when
uo > -1 (see Exercise 7.1), and equations like it have found many applications
ranging from estimates for the time necessary to freeze food to the valuation of
American options. However, from Fig. 7.8, it is easy to see that no real solution
exists when uo < -1 which, like the argument after (7.66), shows that, even
in one space dimension, only a certain amount of supercooling can be tolerated.
This critical value of uo is that which just allows the existence of the travelling
wave (7.94).
7.6.2 Complex variable methods
Complex variable methods can be used to advantage on many free boundary prob-
lems for Laplace's equation. For example, they have been particularly effective in
studying the class of gravity-free, inviscid, irrotational, steady flows introduced as
Helmholtz flows satisfying (7.36). The key point about these flows is that the free
boundary conditions can be written just in terms of the gradient of the potential
0. Hence we can write these conditions trivially in terms of the complex velocity
potential u,(z) = 0 + itl&, where z = r + iy, as
= constant on I
T Z_
= 1. (7.99)
Thus, if we work in the hodograph plane152 of the complex variable dw/dz = u - iv,
then we simply have that w, which is an analytic function of z and hence of
152This term is now introduced for reasons quite different from those in Chapter 4; note that
the axes are now u and -v.

342
FREE BOUNDARY PROBLEMS
dw/dz, has constant imaginary part on part of the unit circle. If this Dirichlet
problem for tb(u, v) can be solved, then its solution gives a functional relation
between w and dw/dz, that is, an ordinary differential equation which reduces to
a quadrature. Unfortunately, the Dirichlet problem also involves the conditions on
any fixed boundaries that may be present in the flow, and these usually become
unmanageable when written in terms of u - iv. However, this disaster is avoided
when any such fixed boundaries are straight. This means that, when we work
with log dw/dz = W (z), say, so that the free boundary is t W = 0, then ' W =
- tan- ' (v/u) is constant on the fixed boundaries. Thus the region of the W plane
corresponding to the fluid flow has a polygonal boundary. But, since 0 is constant
on both the free and fixed boundaries, the same statement can be made about the
geometry of the flow domain in the w plane, which is often just a half-plane. Hence
we can resort to the general Schwarz-Christoffel map to relate W to w; this map is
a particular explicit realisation of the powerful Riemann mapping theorem, which
states that there is a unique conformal map between simply-connected regions in
two complex planes when three conditions are satisfied: the interiors of the regions
must map into each other, the boundaries must map into each other, and three
pairs of boundary points must be identified with each other (see [16]). The details
can be quite intricate (see Exercises 7.14 and 7.15), but the key idea is simple: it
is the uniqueness of the mapping that pins down W(z), and hence dw/dz, as a
function of w. In this way, an extraordinary variety of flows involving single and
multiple jets and cavities can be constructed, subject only to the restriction that
the fixed boundaries are straight; see [4) for a comprehensive description of this
technique.
Almost as effective is the application of conformal maps to another class of
steady flows, namely those through porous media in the presence of gravity, as
modelled by (7.14) and (7.16). Now the free boundary conditions are
p = 0, (7.100)
IVp12+LP = 0,
(7.101)
which again suggests consideration of the hodograph plane dw/dz = u - iv, where
now (u, v) = -V (p + y). The facts that (7.101) states that u2 + (v + 1/2)2 = 1/4
on the free boundary, and that the flow direction is - arg dw/dz, mean that the
flow domain in the hodograph plane is now bounded by a circle and straight lines.
This demands more ingenuity when mapping onto the w plane but many examples
can be solved this way.
It is unfortunate that so few evolution problems are susceptible to conformal
mapping methods. A little progress can be made with one irrotational inviscid
gravity-free flow (see Exercise 7.16) but things are much better for Hele-Shaw
flows. Since these flows are limiting cases of Stefan problems, for which there are
few multidimensional solutions, almost anything we can say in two dimensions is
of great practical value.
The power of the method is most apparent when we consider the problem
of blowing or sucking fluid from a single point, which is the simplest possible

EXPLICIT SOLUTIONS 343
driving mechanism in practice, and can be realised by mounting a hypodermic
syringe in one of the plates of the cell. What we shall be able to do will prove far
more valuable than the Green's function reductions, such as (7.67). That method
allowed us to collapse the problem onto the free boundary, but only in the form
of a `global' integro-differential equation that was to be satisfied there, and from
which it is difficult to find any useful explicit solutions. Using complex variables,
we can write one of the free boundary conditions as a local differential relation
for the mapping function. Although the problem is still global in nature because
of the relationship between the real and imaginary parts of an analytic function,
luckily the Hele-Shaw problem has so much `structure' that we can find a huge
range of explicit solutions.
The argument goes as follows. Assume we can map the boundary of the fluid
region 11 univalently (i.e. one-to-one) onto the unit circle in an auxiliary C plane,
say with z = f ((, t), with the source or sink at z = 0 being mapped to ( = 0.
Then the problem in the ( plane is to find a harmonic function p vanishing on the
unit circle and with the singularity
p ^- -
Q
log ICI
as ICI -> 0,
where Q is the strength of the source. Hence
P= -fit
Q log
(7.102)
and we simply need to find f in order to be able to relate C back to z. To do this
we recall the kinematic condition (7.11), which requires that
aP -
IVPI2 = 0
(7.103)
on the free boundary. Now
2w Op
=
18(I
1 Of lot
Q 8t
Cot
s fixed
C
of/ac'
also, on ICI = 1,
2 2
Q2
IopI2
°
ICI2
I
dz
I
Iof
/a(I2
(7.104)
(7.105)
Thus we arrive at our unconventional differential equation for f in the form
9
CLf 8f
Q (7.106)
8( 8t)
27r
on ICI = 1, with f being analytic in I(I < 1. This formulation enables many free
boundary explicit solutions of the Hele-Shaw problem to be written down. For
example, with
f =a, (t)( + a2(t)C2
(7.107)

344
FREE BOUNDARY PROBLEMS
and a, real, without loss of generality, by equating coefficients on SCI = 1, we find
that
al
dt
+ 2a2 dt =
Q
'
a, dt + 2a2 dt
=
0,
and hence
a, + 24 =
Qt
+ constant,
a2la2 = constant;
a sequence of free boundaries in which a limason at t = 0 terminates in a cardioid
at t = t2 is shown in Fig. 7.9.
Experimentation with such polynomial maps other than multiples of the iden-
tity suggests that any sequence of contracting (suction) free boundaries generated
by these maps terminates before all the fluid is extracted, forming a cusp in the
free boundary, and indeed this can be proved to be true. Perhaps this is not so
surprising since we know that `contracting' Hele-Shaw flows are known to be lin-
early unstable from §7.2.3. What we now see is that nonlinearity seems to do little
to ease their fate and, on the contrary, it engenders finite-time blow-up.
We can now note that the moment conservation (7.63) is a simple deduction
from (7.105) since
dt
fjzmdzdy
=
fzvnds
Fig. 7.9 Cuspidal blow-up for the map (7.107).

REGULARISATION 345
J
I
an
=f
fm 1
Q df
KI=t
Idf/dCI
2a d(
Q r
fn1dC.
J1<1=1
this is zero for m > I because f (0, t) = 0. We should also mention that analytic
continuation methods can sometimes be used to solve (7.106) as a functional differ-
ential equation everywhere within the unit circle; this procedure is closely related
to the idea of the Schwarz function introduced in Exercise 7.18.
This discussion of blow-up leads us to the last topic we wish to mention in
connection with free boundary problems.
* 7.6
Regularisation
We repeat our statement that, more than any others, the partial differential equa-
tion problems discussed in this chapter raise the spectre of ill-posedness as a pos-
sible attribute of everyday models of real-world phenomena. In Chapters 4-6, we
have only cited the backwards heat equation and the Cauchy problem for elliptic
equations as possible examples of ill-posedness, but they are models that rarely, if
ever, occur in practice."J3 As a paradigm, however, the backwards heat equation
is exceedingly helpful because it is easy to analyse by, say, transform methods, and
it enables us to ask the question 'suppose the modelling of a practical problem led
to the backward heat equation with a small extra regularising term, say
at = -a
22 +EJ(u)'
u(z,0) = uo(z); (7.108)
what could we say about the response as e -> 0?1154
As discussed in §6.7.1, one 7 which does indeed regularise the backward heat
equation and make (7.108) into a well-posed Cauchy problem for e > 0 is .(u) _
-r04u/ax4, in which case the Fourier transform solution is
u =
1
yo(k)e-ikx+k21-tk4
dk.
2ir
_x
(7.109)
As e decreases to zero this integral becomes more and more irregular, tending to
a function which may blow up in finite time.
Unfortunately, representations such as (7.109) are unavailable for free bound-
ary problems and their regularisation then represents a challenging area of current
research. In practice. there are always physical regularisation mechanisms avail-
able such as 'surface energy' in phase changes (or surface tension or viscosity in
153This statement
assumes we exclude inverse problems in which we try to 'postdict' the past;
they will be mentioned again in Chapter 9.
154This is
an example of the so-called Tikhonov regularisation of ill-posed problems.
346
FREE BOUNDARY PROBLEMS
free surface flows), surface chemical reactions and several other sources of 'dissipa-
tion'. Indeed, these mechanisms are much more likely to exist near a free boundary,
where the continuum models we have constructed have solutions that change in-
finitely rapidly, than away from it. The mathematical consequence is that higher
derivatives can thereby be introduced into the free boundary conditions. These of-
ten have the advantage of increasing the likelihood of well-posedness, as in (7.109),
but the disadvantage of being difficult to analyse.
The idea of introducing higher derivatives into free boundary conditions is
not the only tool in the mathematician's regularising armoury. Indeed, we have
already seen one dramatic example where a simple reformulation of the Stefan
problem in terms of the enthalpy, as in (7.84), eliminated superheating. This was
achieved at the expense of introducing new free boundaries and a mushy region
into the solution. It is equally possible to smooth out the free boundary altogether,
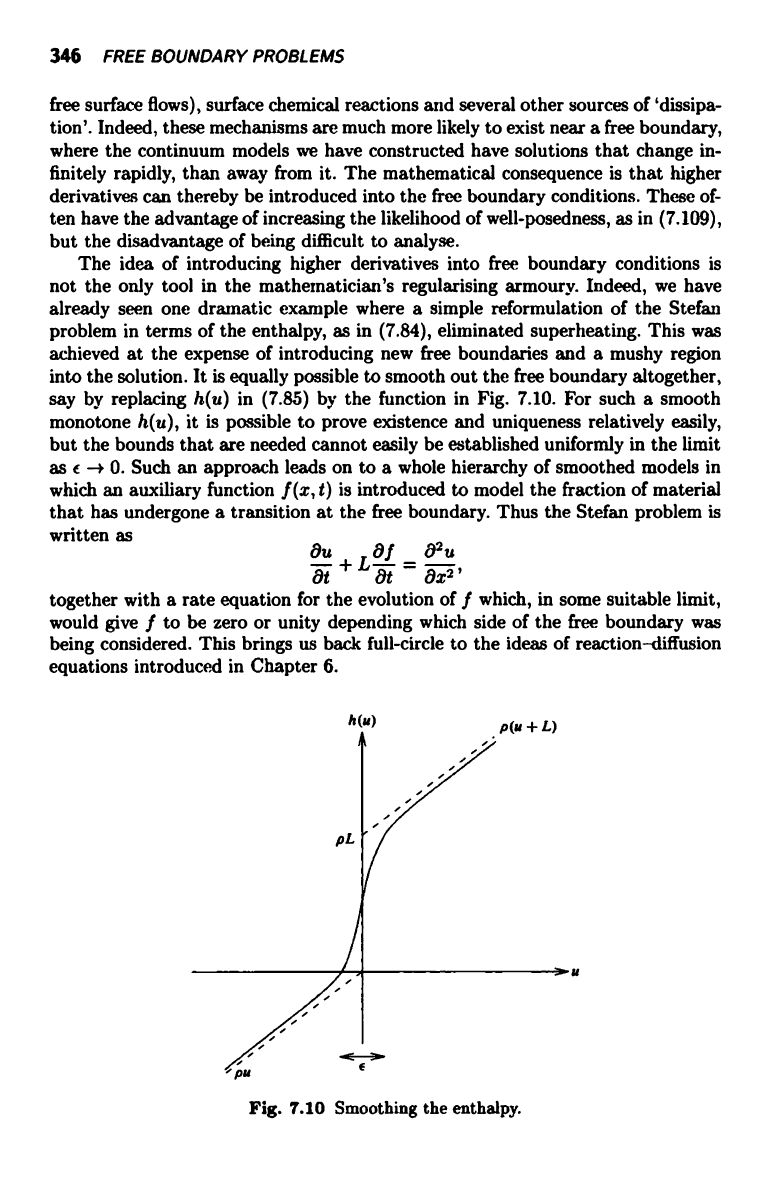
say by replacing h(u) in (7.85) by the function in Fig. 7.10. For such a smooth
monotone h(u), it is possible to prove existence and uniqueness relatively easily,
but the bounds that are needed cannot easily be established uniformly in the limit
as c -+ 0. Such an approach leads on to a whole hierarchy of smoothed models in
which an auxiliary function f (x, t) is introduced to model the fraction of material
that has undergone a transition at the free boundary. Thus the Stefan problem is
written as
au of a2u
at +
L
at = 8x2,
together with a rate equation for the evolution of f which, in some suitable limit,
would give f to be zero or unity depending which side of the free boundary was
being considered. This brings us back full-circle to the ideas of reaction-diffusion
equations introduced in Chapter 6.
h(u)
p(u + L)
pL
3u
WPu
Fig. 7.10 Smoothing the enthalpy.

POSTSCRIPT 347
Finally, we remark that we could make an even more radical regularisation of
the superheated or supercooled one-phase Stefan problem by identifying it with an
oxygen consumption problem, as in (7.80). We have seen that this identification
can be made as long as the concentration c is allowed to change sign. However,
we could restrict c to be positive, thereby making the oxygen consumption model
well posed, but this might entail the generation of extra components of the free
boundary. Hence, if we allow the Stefan problem to admit new components in its
free boundary in precisely the same way, then we are performing a regularisation
by `nucleation'.
* 7.7
Postscript
We conclude this chapter with a brief introduction to a special class of free bound-
ary problems of wide practical applicability but whose mathematical character is
quite different from most of those discussed hitherto. These are problems in which
the free boundary has two dimensions fewer than the dimensionality of the govern-
ing partial differential equations. Hence they can be called codimension-two free
boundary problems, in contrast to the codimension-one problems of §7.1.
We have in fact already encountered such configurations in our discussion of
contact problems in elasticity. However, contact problems are special in that the
free boundary is constrained to lie in the prescribed surface in which contact occurs,
and it is quite possible for a one-dimensional free boundary to move more freely
in three-dimensional space. Such situations arise in modelling materials such as
superfluids and superconductors, but they are most readily visualised by looking
at the motion of vortices in water. We recall from §5.1.4.1 that the model for such
a vortex in two-dimensional inviscid flow involves finding a velocity potential i
which has a singularity of the form, say,
2
near a vortex at the origin of polar coordinates (r, 9). Put in terms of distributions,
the velocity v and stream function
' satisfy
v = curl (0, 0, 0) , curl v = (0, 0, -V2 ') = (0, 0, 6(x)), (7.110)
where x = (x, y), together with initial and boundary conditions away from the
origin. This model is adequate for a vortex whose position is given a priori, but,
if the vortex is free to move, then extra information is needed before we can
formulate a free boundary model for its dynamics. In two dimensions this comes
from Helmholtz' law which, crudely speaking, asserts that the vortex responds to
the regular part of VO, i.e. that a vortex whose position is x(t) moves such that
dt -
xlimtly
( - 2
) ,
(7.111)
when 0 is now measured relative to x(t).
`Unfortunately, this law, which asserts
that the vortex moves with the `regular part' of the local fluid velocity, is difficult
to justify without a complicated asymptotic analysis.
