Ockendon J., Howison S., Lacey A., Movchan A. Applied Partial Differential Equations

Подождите немного. Документ загружается.

358

FREE BOUNDARY PROBLEMS

so that its velocity there is (V, 0). Show that, if z = f (S, t) maps the fluid

region onto I(I < 1 and the sink at x = +oo is mapped onto S = 0, then

f ((, t) = - log( +O(1) as S -+ 0, and that Q in (7.106) is replaced by -2rV.

Use (7.106) to show that the map

z=f(C,t)

-log( +2(1-A)log\1

2S)

gives a travelling wave solution, moving with speed U = V/A, for any value

of A between 0 and 1. Set t; = ei9 to show that the interface has the equation

e(:-Ut)/2(1-a) = cosy/2A) and hence show that

as z -+ -oo the interface is

asymptotic to the lines y = fAir.

Remark. There is an exact unsteady solution in which a small, nearly sinu-

soidal perturbation to a planar interface evolves into this Safman--Taylor

finger as t -+ oo. The value of A is not specified by the simple model we

have used, and the question of its determination is an example of `pattern

selection'. Note that the value A = 1/2, which is often seen in experiments,

gives the Grim Reaper solution of curvature flow (see Exercise 6.33).

7.20. When gravity is important in a Muskat problem, the free boundary condi-

tions are

Pw = Po,

-Kw

(Pw + Pw9y) _ K.

(Po + Pogy) = VII,

where pw and po are the pressures on either side of the boundary, Kw,o =

kw,o/µw,o and y is vertical. Show that a travelling wave solution exists in

which the free boundary is y = V t and

(

P. = -

Pw9)

(y - V0,

P. = -

+ Pog) (y - V0.

\ Ko

Show that, if the free boundary is perturbed to y = V t + ee°t sin kx, k > 0,

and f is small, then

- 9KwKo(Po - Pw) + (Kw - Ko)V

K. + K.

and deduce that, even if a heavy and more viscous fluid overlies a light one,

the flow is stable if V is sufficiently large and negative.

7.21. Show that the principal normal n and binormal b of (7.114) are

n = (- cos(s - wt), - sin(a - wt), 0),

+ b2

(bsin(s - wt), -bcos(a - wt), a),

and that the curvature is a/(a2 + b2). Deduce that the velocity of a point

on (7.114) satisfies (7.113) as long as

V+

1 log do

a2 +

Non-quasilinear equations

8.1

Introduction

Several practical situations give rise to partial differential equations that are not

quasilinear. For example, suppose u(x, y) is the elevation of a pile of dry sand

that is heaped on a table in limiting equilibrium, so that if any more sand was

poured from above it would slide off. Then the angle between the normal to the

surface u = u(x, y) and the vertical (0, 0,1) is a prescribed constant -y, the angle

of friction, so that

I//

\ 2

(,U),) s1 -1/2

I8 J

= cost.

With a slight change of variables, this can be transformed into the famous eikonal

equation

()2

+ \/a

1. (8.1)

There is another application of (8.1) that has implications far beyond those for

sand piles. This concerns approximate solutions of Helmholtz' equation describing

wave propagation in the frequency domain. We recall that the equation was derived

from the wave equation 820/8r2 = aSV24 by writing

0 =

(e"'+'(x, y))

(8.2)

where we have replaced t in the wave equation by r to avoid later confusion in

notation. In dimensionless variables this gives Helmholtz' equation

(V2 + k2)lp = 0,

(8.3)

as in (5.27), where k = wL/ao and L is a characteristic length scale over which

the waves propagate. Now, for the propagation of light, w/aa 107 m'1 typically,

and so, on an everyday length scale for which L - 1 m, k is large. In this case,

the asymptotic approximation of Helmholtz' equation is called the theory of geo-

metric optics. It relies on the WKB asymptotic procedure for ordinary differential

equations, which suggests that we write

tPA(x, y; k)e"k"(=,v) as k i oo, (8.4)

359

360

NON-QUASILINEAR EQUATIONS

so that

Vii - (ikAVu + VA)eik",

V2ii _ (-k2AIVU12 + 2ikVA Vu + ikAV2u + V2A)eik",

and equating terms of 0(k2) leads at once to (8.1) for u.157

Equation (8.1) also has its origins in the less well known, but no less interesting,

problem of heat conduction over short time intervals. We have seen in (6.35) that,

in an infinite two-dimensional medium, the response to a heat source at x = y =

t = 0 is the Green's function (1/47rt)e-(=3+12)/°t. Thus, when there are boundaries

in the problem, we are motivated to try the WKB ansatz

T , _

v(Z.y)/t

in the heat conduction equation aT/8t = V2T to give, to lowest order as t -+ 0,

Cex)2+C8y)2

Thus u = 2v'V satisfies (8.1).

In the light of the models above, we expect the solutions of (8.1) to have inter-

esting properties, since they should predict geometrical shapes ranging from the

topography of heaps of granular materials to the patterns of light rays. Certainly,

non-quasilinear ordinary differential equations often have properties that are much

more interesting than quasilinear ones, as demonstrated in (32).

In one sense, however, there is no need to devote a chapter to this topic because,

as explained in Chapter 2, any partial differential equation can always be written

as a quasilinear system. However, this can often only be done at the expense of

cross-differentiation, which leads to loss of information and a greatly expanded

system; also, from the practical point of view, it is much easier to interpret mathe-

matical predictions in terms of the basic physical variables rather than complicated

derivatives thereof.

8.2

Scalar first-order equations

8.2.1 Two independent variables

We recall from §1.3 that the quasilinear first-order equation

bau

8x8

= c

could be approached by exploiting either its geometrical interpretation or the ease

with which all the derivatives of u can be computed in terms of known Cauchy

'"Those familiar with the 'stationary phase' approximation to Fourier integrals will be able

to show that, when a Fourier transform solution of (8.3) is available, its high-frequency limit is

often dominated by the contribution from a saddle point whose location is found by a procedure

precisely equivalent to the solution of (8.1) by Charpit's method, as described in the next section.

SCALAR FIRST-ORDER EQUATIONS 361

data. Neither of these options is immediately open when we study equations of

the form

F(x, y, u, p, q) = 0,

(8.6)

where p = au/ax and q = au/ay. Moreover, our earlier theory suggests that there

is little chance of reducing (8.6) to a system of ordinary differential equations as

we could in the quasilinear case. We say this because cross-differentiation leads to

the system

OF Op

OF aq

aax + aa

OF OF

a-Pa

(8.7)

OF Op OF aq OF OF

-=--

-q

(8 8)

aPay ga 8y

=P,

(8.9)

=q,

(8.10)

Op Oq

(8.11)

for the vector w = (u, p, q)'. Hence, when we choose three suitably independent

equations from this set, as will be done below, we expect to be in the situation

described in §1.3; only very rarely would a system of partial differential equations

with three scalar dependent variables be integrable along characteristics. However,

(8.7)-(8.11) is a very special system, as we will see shortly.

From the geometrical point of view, (8.6) is much more complicated than (8.5).

It says that the normal to the solution surface at each point must lie in a cone

(called the normal cone, despite possible confusion with §2.6) since, when we

`freeze' x, y and u, (8.6) is a relation just between the direction cosines of the

normal to the solution surface u = u(x, y). Only in the quasilinear case does the

normal cone degenerate into a plane.

Let us now address the Cauchy problem of determining w from a knowledge

of its values on an arbitrary curve in the (x, y) plane. Using t to parametrise the

characteristics, we soon find that the partial derivatives of w must also satisfy the

relations

(8.12)

(8.13)

(8.14)

where, as usual, ' = d/dt. We can discard (8.9), (8.10) and (8.12) for the time

being because, together with (8.6), they are consistent equations for au/ax and

362

NON-QUASILINEAR EQUATIONS

Ou/Oy. Furthermore, by eliminating Op/Ox and Oq/Oy, the remaining equations

can be written as

OF Op OF Oq -

- x

--y

t OF

OF1

(8.15)

Ogex

iWaj

OF Op OF Oq

= -i

-y

+ x

`Oy

(OF OF) OF

-n

+ P

16)

8g 8x

ap 8y

ap ,

8x au

Op Oq =o

(8.17)

Oy Ox

The characteristics are, as usual, defined as the curves on which the normal deriva-

tive of w is not determined uniquely by (8.6) and its value on the curve; hence,

on a characteristic,

OF OF

. OF

-xaq =

(8.18)

Moreover, consistency in (8.15)--(8.17) requires that the right-hand sides of (8.15)

and (8.16) be equal and opposite and hence zero, by (8.18).

Lastly, we have freedom to choose our parameter t, and easily the most conve-

nient choice is to make

so that

_ OF

The consistency conditions now reduce to

OF OF

P=-8x -Pau, q=-ay -qau,

and finally we return to (8.12) to see that

OF OF

u=pap +qaq.

Gathering these equations together, we have

OF OF OF OF

x= 8P, y= a, u=Pa+qa,q

OF OF OF OF

P=-8z -Pau, qay -qau,

(8.19)

and these are called Charpit's equations. Given appropriate initial data at t = 0,

they have a unique solution, at least for small t, but, whereas this initial data was

readily available in the quasilinear case, it now demands knowledge of p and q as

SCALAR FIRST-ORDER EQUATIONS 363

well as u at the initial curve t = 0. To be precise, given Cauchy data x = xo(s),

y = yo(s) and u = uo(s), we need to be able to solve the two equations

F(xo, yo, uo, po, qo) = 0 and

uo = poxo + g0yo

simultaneously for po and qo, where' = d/ds, and the non-vanishing of y'OF/Op-

.c' OF/Oq is the condition for local solvability, as already revealed in (8.18). Then,

if we write the corresponding solution of (8.19) as

x = x(s, t),

y = y(s, t),

u = u(s, t),

p = p(s, t),

q = q(s, t)

and if IO(x, y)/O(s, t) I is neither zero nor infinite, we assert that

the result of eliminating s and t gives the solution u = u(x, y) of the partial

differential equation F(x, y, u, p, q) = 0.

If this statement is true, it is a spectacular result because we have reduced the

task of solving an arbitrary scalar first-order partial differential equation with

two independent variables to that of solving five autonomous ordinary differential

equations, something which, as mentioned above, we have no right to expect. We

must clearly scrutinise the statement much more closely but, before we do that,

we issue two warnings.

Firstly, the determination of po and qo is almost certainly non-unique unless

the original equation (8.6) is quasilinear. Hence, as with non-quasilinear ordinary

differential equations, extra information is usually needed before we can begin our

integration of Charpit's equations.

Secondly, since the ordinary differential equations (8.19) are nonlinear, it is

quite likely that their solution blows up at some finite time or, even if it exists

globally, it may possibly behave chaotically. The same was true for the quasilinear

case but now, when we consider the global structure of the solution, we may expect

singularities other than 'shocks' to be capable of developing.

Let us now return to our assertion above. Its justification requires not only that

we verify that u explicitly satisfies (8.6), but also that w is such that p = Ou/8x and

q = Ou/Oy. since these relations are not guaranteed by the assertion (remember

that p and q were originally introduced by these relations, but from (8.7) onwards

we have been thinking of w as a vector with three independent components). The

verification that w satisfies (8.6) is immediate since

_ OF.

OF. OF OF OF.

Oxr+ Oyy+ Ouu+ Opp+ Oqq=

on using (8.12)-(8.14); at t = 0, F = 0, so that F = 0 for all t and s, and hence

for all x and y.

To show that p = Ou/Ox and q = Ou/Oy, it is sufficient to show that ft = p1+6

and u' = px' + qy'. The former condition is immediate from (8.12)-(8.14); for the

latter, we consider the function O(s, t) = u' - px' - qy'. Then, differentiating 0 and

using the partial derivative of u. = pi + qy with respect to s, we have

364

NON-QUASILINEAR EQUATIONS

=p'i+q'y_px'-Q,y'

= BFx,

BFy,

OF,

(x + 4U,)

8y 8p 8q

8s -

8u '

where OF/8s is calculated keeping t constant. But F e 0, so that 8F/8s = 0; also

¢ = 0 at t = 0. Hence -0 = 0 for all t (no matter what the function 8F/8u is) and

u' = px' + qy', so that p and q are indeed the derivatives of u.

We can now generalise our definition of characteristics by saying that Charpit's

equations (8.19) define characteristics in the five-dimensional space (x, y, u, p, q),

or, equivalently, a characteristic strip in the three-dimensional (x, y, u) space. That

is, at each point (x, y) a surface element is defined, and the solution surface is

formed by 'glueing together' the characteristic strips. This solution only exists

where the Jacobian I8(x, y)/8(s, t)I # 0, that is when

8OF

# y'

-5p7,

(8.20)

and, as already mentioned, this condition must be satisfied by the Cauchy data.

(A simpler derivation of (8.14)-(8.20) for the case 8F/8u = 1 is given in (5) and

Exercise 8.5.)

A geometrical derivation of Charpit's equations follows from the observation

that the dual cone of the normal cone, that is the cone which is the envelope of the

planes normal to each generator of the normal cone, touches the solution surface

at each point. The solution surface is therefore the envelope of all these dual cones

(which are also called Monge cones). For the quasilinear case the normal cone is a

plane since ap+ bq = c, and its dual degenerates into a line in the direction (a, b, c)

which must be tangent to the solution surface. In the fully nonlinear case we may

construct this Monge cone by finding the envelope of the planes (x - x' )p + (y -

y')q = u - u' through the point (x', y', u') and subject to F(x*, y', u', p, q) = 0.

As in §2.6, the envelope is given by

x-x'=Aa

y-y*=Ar'

where p, q and A must be eliminated between these four relations. Eliminating A,

we obtain

x-x' _ y-y' _ u-u'

8F/8p 8F/8q p 8F/8p + q OF/8q'

and thus a small vector (bx, by, du) lying in a characteristic strip satisfies

8x _ by

= bt

8F/8p

F/8q

p 8F/8p + q 8F/8q

say, for (x, y, u) near (x', y', u'). We cannot eliminate p and q, but we can obtain

expressions for by and bq given by

SCALAR FIRST-ORDER EQUATIONS 365

8x -

OF)

(

by =

bx +-y

by = bt

8u J

bq =

8q6x

8qby

= 6t (_

OF )

a-8y5 -95 ,

using (8.7)-(8.11). Finally, letting bt -+ 0, Charpit's equations (8.19) are recovered.

This discussion clearly reveals the existence of the so-called integral conoids

formed by all the characteristics passing through a given point in (x, y, u) space.

The integral conoid is the global extension of the Monge cone at that point and

the solutions of the Cauchy problem for (8.6) can also be thought of geometrically

as the envelope of all the integral conoids through the initial curve. As indicated

in Fig. 8.1, this construction reveals the non-uniqueness we mentioned earlier in

this section, and the situation could be far more complicated than that for the

single-sheeted conoids that we have sketched.

A final general remark concerns those situations in which we may be unable

to solve Charpit's equations yet we may be lucky enough to be able to guess a

two-parameter family of solutions of (8.6) in the form u = f (x, y; a,#). Then it is

easily verified that the eliminant of a between

u = f(x,y;a,f(a))

and

8a + do Lf

a 0,6

is also a solution for any function 9(a). Thus, if a solution to (8.6) with two ar-

bitrary constants can be found, then many more solutions can be generated by

different choices of $(a). Indeed, as mentioned in §1.9, we expect the general solu-

tion of any first-order partial differential equation with two independent variables

to contain at least one arbitrary function of one variable in this way. In the quasi-

linear case considered in §1.5, the general solution was obtained by setting one

constant of integration of the characteristic ordinary differential equation to be an

(a)

Cauchy data prescribed on initial curve

(b)

Fig. 8.1 Solution of the Cauchy problem: (a) the quasilinear case; (b) the non-quasilinear

case.

366

NON-QUASILINEAR EQUATIONS

arbitrary function of the other. In general, however, Charpit's equations demand

that a more elaborate procedure be followed.

8.2.2

More independent variables

While the arguments above could never be extended to either scalar higher-order

equations or vector equations, the generalisation to m independent variables is

quite painless. Changing notation to

F(x;, u, p;) = 0,

where p; = 8a for i = 1, ... IM,

(8.21)

Charpit's equations are simply

x; _

(8.22)

ap;

OF OF

Pi = -

ax; - p' au '

(8.23)

u=Ep;-. (8.24)

1 aPi

Anyone familiar with classical mechanics can now make an observation: if F is

independent of u, then (8.22) and (8.23) are simply Hamilton's equations for a

mechanical system in which x; are generalised coordinates, p; are generalised mo-

menta and F is the Hamiltonian. Since it is easy to generalise our assertion that

Charpit's equations give the solution of the partial differential equation to this

case, we have thus derived the remarkable result that any problem in classical

mechanics with a finite number of degrees of freedom is equivalent to a scalar

first-order partial differential equation in which OF/au = 0. We will explore the

implications of this further in §8.3.

We remark that, even though the Cauchy problem involves data specified on

an (m -1)-dimensional surface, the solution of (8.21) is still expressed in terms of

ordinary differential equations which hold along the one-dimensional curves that

we have called characteristics. This situation is a generalisation of that in §1.8

and hence, when m > 2, it is reasonable to call these one-dimensional curves

bicharacteristics, reserving the adjective characteristic for surfaces of dimension

m-1.

The preceding theory paves the way for many exciting investigations into a

great variety of problems in science and industry, and we now describe some of

these, beginning, as always, with the simplest configurations.

8.2.3 The eikonal equation

Charpit's equations are greatly simplified when F does not depend explicitly on

x, y and u. In this case, p = 4 = 0 on a characteristic, so that p = po(s), q = qo(s)

and the characteristic projections in the (x, y) plane, often called rays, are straight

lines with slope (OF/Oq)0 / (OF/Op)o (as usual, the suffix zero denotes values on

the initial curve). On these rays,

SCALAR FIRST-ORDER EQUATIONS 367

COF) rOF) r 8F 8F)

x=xo+t

y=yo+t aq J u=uo+tlpap

+g57

(8.25)

and the solution may be obtained by first eliminating t and then s. The solution

surface is a special case of a ruled surface since, at each point, there is a straight

line lying in the surface; such surfaces will be discussed again in the final section

of this chapter.

8.2.3.1 Sand piles

When (8.1) is used to model a sand pile on a horizontal base, the boundary condi-

tions are u = 0 on x = xo (s), y = yo (s). 158 Thus pox'+qoy'=Oand po+qo =1,

so that

fyo

Po -

((x0I )2

(yp)2)1'2

where the sign must be chosen so that the sand pile lies in u > 0. The ray equations

(8.25) reduce to

x = 2tpo + xo,

y = 2tgo + yo,

u = 2t,

and, assuming the base has a smooth boundary, the solution can be obtained

locally by eliminating s between x - xo = upo and y - yo = uqo. This may not be

at all simple to do explicitly and we consider two special cases.

For a circular base, we have

xp = COS s, yo = Sin s,

and we find

and

po = - cos s, qo = - sins

u = 1 - (x2 +Y

2)1/2.

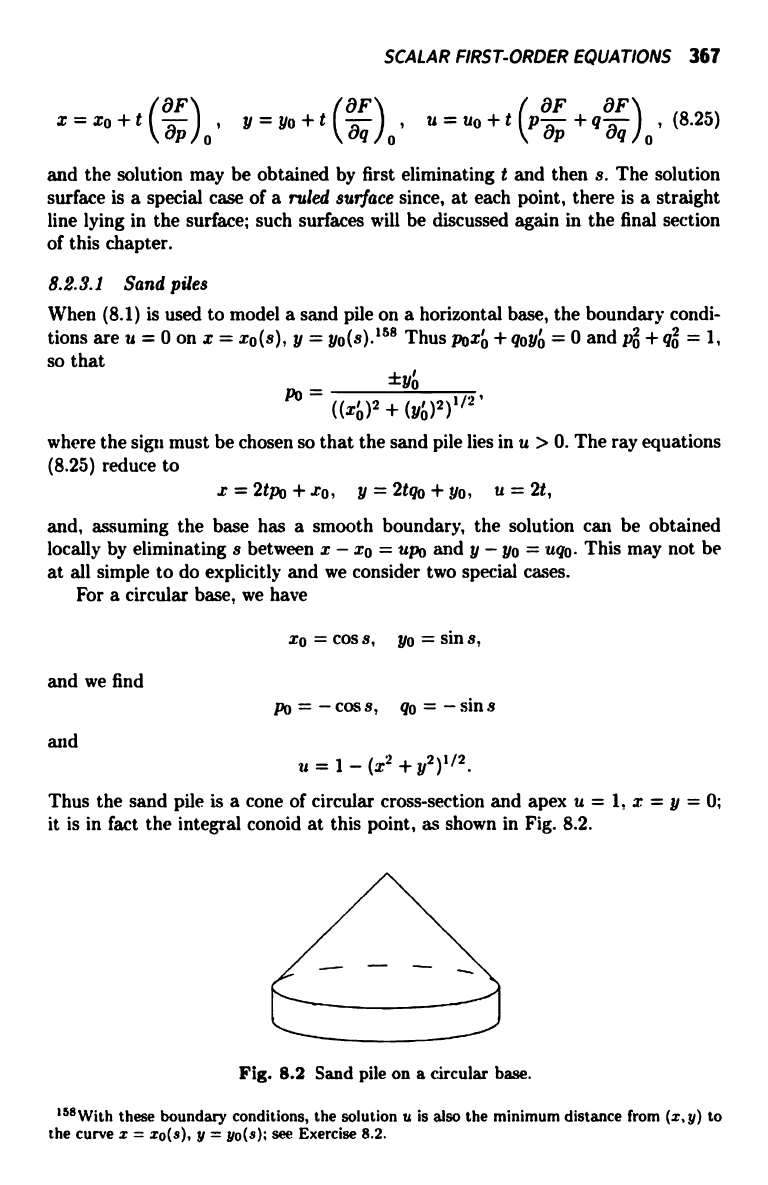
Thus the sand pile is a cone of circular cross-section and apex u = 1, x = y = 0;

it is in fact the integral conoid at this point, as shown in Fig. 8.2.

Fig. 8.2 Sand pile on a circular base.

158With these boundary conditions, the solution is is also the minimum distance from (x,y) to

the curve x = xo(s), y = yo(s); see Exercise 8.2.