Nof S.Y. Springer Handbook of Automation

Подождите немного. Документ загружается.

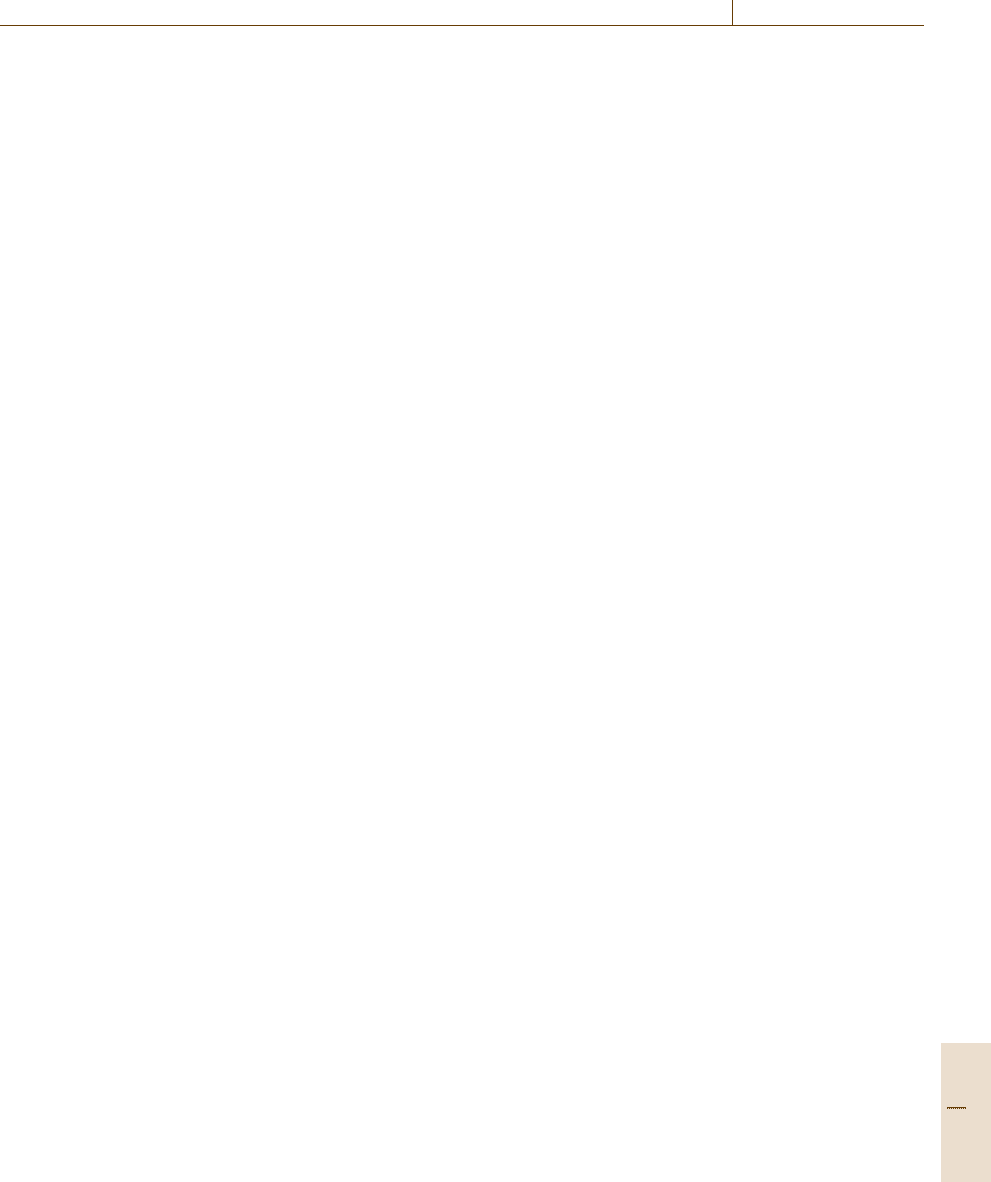
Material Handling Automation in Production and Warehouse Systems 55.2 System Architecture 965

tem (WMS), and enterprise resource planning (ERP)

system. The WMS can be substituted by the MMS

if the warehouse is composed of relatively simple

systems.

Understanding high-level decision-support systems

in SCM helps to understand the scope of control

tasks performed by the IAMHS. The advanced plan-

ning and scheduling (APS) system generally consists

of planning and scheduling modules. Sometimes the

scheduling module is again broken down into schedul-

ing and dispatching modules (SDS in Fig.55.3). The

ERP system generally includes the planning module;

however, the scheduling and dispatching modules can

be included in any other systems such as the MES and

WMS.InFig.55.3, it is assumed that the modules are

running in a stand-alone system called the SDS that

communicates with the ERP system, MES,andMMS.

The planning module makes a long-term production or

procurement plan based on customer orders, demand

forecasting results, and capacity constraints. Its time

horizon varies from weeks to months. Practically, it

hardly optimizes complex factors of resources on the

shop ﬂoor because of the long computation time, but

constructs highly aggregated planning. Its results in-

clude production quantities for each product type and

time bucket, or production due dates for each product

type or product group. Detailed resource requirement

plans are not speciﬁed by the planning module due to

the uncertainties and complexities of operations. The

scheduling module is responsible for delineating more

concrete plans for the shop ﬂoor to meet the target pro-

duction plan from the planning module. It typically tries

to optimize various resource constraints with several

objectives such as due-date satisfaction and through-

put maximization. Detailed resource requirement plans

over time buckets within a time horizon are created by

the scheduling module. It sometimes takes into account

constraints in the AMHS for more robust scheduling.

The time horizon of the scheduling module varies from

a few hours to days. Thedispatching moduledetermines

the best unit load for a machine in real time following

a trigger event from the machine or unit load. It tries

to follow up closely the scheduling results, which are

globally optimized. The MMS in the IAMHS receives

transfer commands from either the scheduling module

or dispatching module based on its system architec-

ture. These transfer commands are the result of the

scheduling, machine assignment or job sequencing on

processing machines. The MMS manages the process

of the given transfer command by creating more de-

tailed transfer commands to the AMSHs in the IAMHS.

The dispatching module is sometimes included in the

MMS, and creates the transfer commands based on the

scheduling results and its own dispatching rules for the

real-time status of the shop ﬂoor. The IAMHS takes

charge of the ﬁnal execution of the SCM in an enter-

prise and also provides useful information as described

above.

The higher-level systems of the IAMHS auto-

mate information processing throughout an enterprise.

The MES in Fig.55.3 is a tracking system that col-

lects important data from processing machines and

stores them in well-structured database tables for ana-

lysis of quality and process controls; however, it has

expanded its role into many other areas based on

a powerful open architecture. It has been popularly

used in the electronic industry such as in semicon-

ductor fabs and surface-mounting technology (SMT)

lines, and has recently spread into other industries.

The warehouse management system (WMS)isgen-

erally used in mid- or large-size warehouse facilities,

similar to MES for a production shop ﬂoor; it tracks

every movement of materials and support operations

for material handling in the warehouse. Its focus is on

information processing automation. The objective of

implementing an ERP system in a company is infor-

mation sharing for rapid and correct decision-making,

and implementation throughout the enterprise by us-

ing an integrated database system [55.12]. Chapter 90

provides a more thorough discussion of ERP and re-

lated concepts. The whole procedures of order entry,

production planning, material procurement, order de-

livery, and corresponding cash ﬂow are managed by

the system. All the data from different applications in

an enterprise or between different enterprises are ex-

changed by an electronic data interchange (EDI) server,

which allows automated exchange of data between ap-

plications. Based on the EDI technology, applications

freely exchange purchase orders, invoices, advance ship

notices, and other business documents directly from

one business system to the other without human sup-

port. Figure 55.4 illustrates the connectivity of IAMHS

to other systems in SCM, which is used in an actual

industry.

55.2.1 Material Management System

The role of the MMS is very important in a complex

IAMHS for high-level automation. The main functions

of the MMS are summarized below, in increasing or-

der of importance. This summary does not discuss the

dispatching module that assigns unit loads to process-

Part F 55.2

966 Part F Industrial Automation

Production line

Genetic algorithm (GA)

palletizing system

Wireless

mobile phones

Wireless

in-vehicle terminals

Transport planning

support system

Vehicle dispatch

system

Logistics

data server

Wireless terminal

system

Terminals Printer

ERP

HOST

EDI

Fig. 55.4 Connectivity of IAMHS to other systems in SCM (courtesy of Murata Machinery)

ing machines because this involves so many topics;

however, the dispatching functions bounded to AMHSs

(i.e., dispatching unit loads while not considering pro-

cess machines) will be discussed here.

The roles of the MMS in a complex IAMHS are:

1. Determining thebest destination amongseveral pos-

sible AMHS alternatives

2. Determining the best route to get to the destination

from a source location via several AMHSs

3. Determining a proper priority for the transfer

command

4. Storing and reporting various data using a database

server

5. Transfer command management between different

AMHSs

6. Error detection and recovery for the transfer

command

7. Providing a user interface for control, monitoring,

and reporting.

Conveyor #1

Machine #9

Machine #8

AGVS #3

AS/RS #4

Machine #5

AGVS #2

AS/RS #3

Machine #4

Machine #2

Machine #1

AGVS #1

AS/RS #2

OP0201

AS/RS #1

OP3

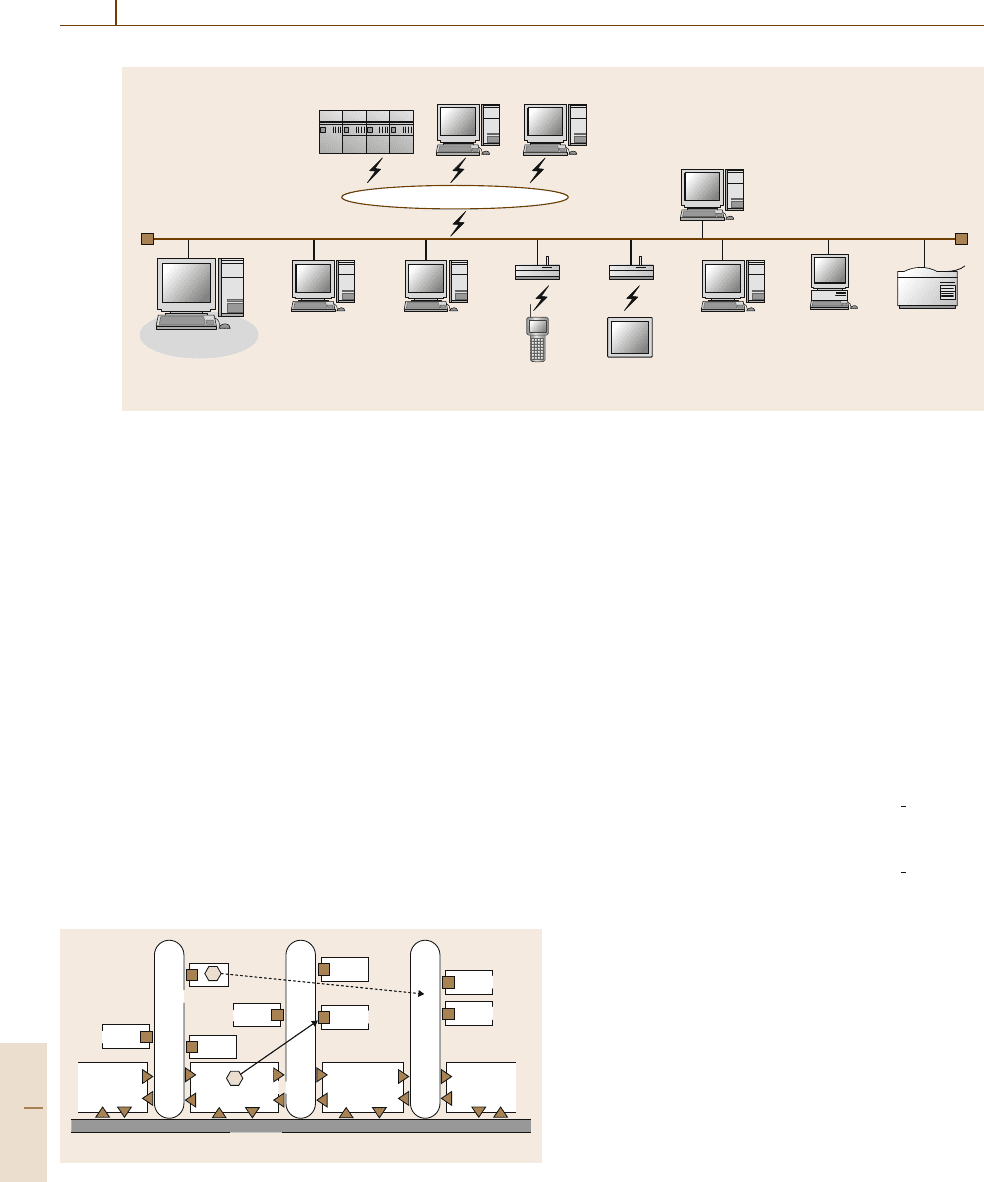
Fig. 55.5 Example of IAMHS

For a unit load to be transferred, its source and

destination locations are mainly determined by the dis-

patching or scheduling module; however, when the

candidate destinations are AMHSs, it is sometimes

more efﬁcient for the MMS to determine the ﬁnal des-

tination than for the scheduling or dispatching module

to do so. Consequently, the dispatching and scheduling

system provides a destination group to the MMS.Fig-

ure 55.5 illustrates the execution process of a transfer

command. In the ﬁgure, if a unit load from Machine #2

has just ﬁnished its processing and has to be trans-

ferred to an AS/RS to be processed next, on one of

the machines connected to AGVS #3 (dashed arrow in

the ﬁgure), there are two candidate AS/RSs connected

to AGVS #3: AS/RS #3 and AS/RS #4. The AS/RS

group connected to AGVS #3 is named AS

Group #3.

The MMS will receive a transfer command from the

dispatching module, specifying the source location as

Machine #2 and the ﬁnal destination as AS

Group #3.

Since there are two alternative destinations, the MMS

may consider the product type of the unit load, the full

rate of each AS/RS, the load port status of each AS/RS,

the shortest distances from the unit load to the AS/RSs

considering current active jobs in each system, and so

on. It will determinethe bestAS/RS amongst thetwo al-

ternatives and trigger a transfer command to AGVS #1,

which will ﬁrst move the load to AS/RS #1 from Ma-

chine #2.

The MMS is also responsible for determining

the destination subsystem in an AMHS, such as the

load/unload port (or pickup/drop-off port) in an AS/RS,

because there are generally multiple load/unload ports

with different types and numbers of buffers. The ports

Part F 55.2

Material Handling Automation in Production and Warehouse Systems 55.2 System Architecture 967

may differ, being load only, unload only or of uniﬁed

type. Assume that a unit load in AS/RS #2 in Fig.55.5

has to be moved to Machine #5, connected to AGVS #2

(solid arrow in Fig.55.5). First, the unit load has to be

moved to one of the output ports in the AS/RS. The

AS/RS controller may not know which output port will

be the best among the three possible ones in the ﬁgure

because it does not know the next destination of the unit

load. The MMS may determine a load port connected to

AGVS #2, OP0201 in Fig.55.5. In practical application,

the problems aregenerally muchmore complicatedthan

this illustration due to the increased instances in the sys-

tem. Few studies have addressed this type of problem.

Sun et al. [55.13]andJimenez et al. [55.14] stress the

importance of this problem in the literature and intro-

duce a few ideas being used in practical applications;

however, their methods leave much room for improve-

ment in that they use static approaches and consider

limited factors.

Obtaining the best route to get to the destination

is another important task of the MMS.Inacomplex

IAMHS, there are many possible routes consisting of

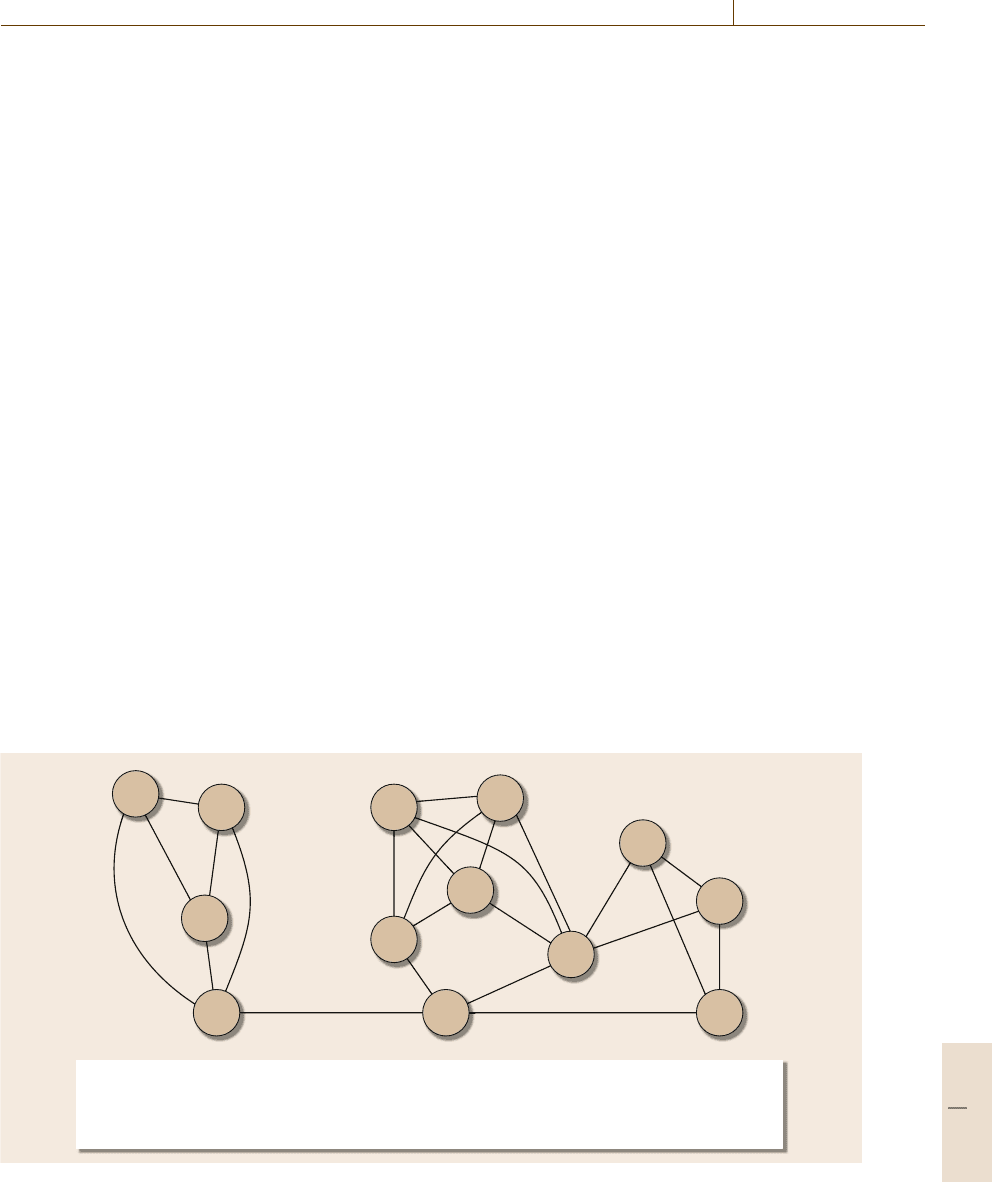
different AMHS types. The IAMHS in Fig. 55.5 is rep-

resented by the graph in Fig. 55.6. A graph can be

encoded in database tables by using an adjacency ma-

trix or incidence matrix for use by a computer program.

The adjacency matrix is a simple from–to chart be-

tween a pair of vertices, in which the value of an edge

is the distance between the vertex pair, being zero if

the pair are not connected. The incidence matrix rep-

Naming convention of vertices in the graph:

Two-digit number in a vertex followed by alphabets represents the index number of machines or AMHS.

For example, M01 is the machine #1 connected to AGVS #1 and CS 01 is the conveyor #1. Acronyms are

as follows. M: Machine, AS: AS/RS, CS: Conveyor System

Fig. 55.6 Graphical representation of the IAMHS in Fig.55.5

resents the connectivity of vertices by edges. Using

a graphical representation of the IAMHS, many pre-

deﬁned properties and algorithms of graph theory can

be applied to develop algorithms for the MMS;for

example, Dijkstra’s algorithm can be used to deter-

mine the shortest path from a source to destination

location.

The time intervals between the arrivals of transfer

commands are sometimes completely random in that

there are signiﬁcant ﬂuctuations in the number of ar-

rivals during different time periods. When the queue

size increases on AMHSs, use of different priorities for

transfer commands often providesa very useful solution

to improve overall system performance. It is reported

that a good priority algorithm can improve the through-

put of a production facility [55.15].

There are two types of tables in the database of

the MMS. One type of table stores parameters for con-

trol algorithms and status user interfaces (UIs). These

need a minimum number of entities to achieve a shorter

transaction time when they are queried. The other type

of table stores data for movement histories based on

communication messages between component systems

of the IAMHS. The accuracy of these historical data

have been signiﬁcantly improved by material handling

automation with advanced information interface tech-

nology (IIT) by using RFID technology or barcode

systems. A large amount of information can be ex-

tracted from the historical data, including the standard

operating time of a machine, the processing routes of

Part F 55.2

968 Part F Industrial Automation

a unit load over machines in different process stages,

the lead time of the unit load from start to ﬁnish, etc.

These data provide useful information for var-

ious purposes. Most of all, without accurate data

from production and warehouse systems, it is hard to

achieve successful realization of the enterprise-level de-

cision support systems explained above. Good planning

strongly depends on accurate data. In practice, many

companieshaveinvestedinexpensiveERP systems ca-

pable of automated production planning for their shop

ﬂoors; however, many of them do not use the module

because of poor planning and scheduling quality from

the system. One of the main reasons for this poor quality

is sometimes due to the lack of good data from the ma-

terial handling system, which relies on manual jobs and

operator paperwork. Accurate data from AMHSs also

helps to achieve lean manufacturing on the shop ﬂoor

by providing precise measures. For a complicated shop

ﬂoor, it is often difﬁcult to deﬁne a bottleneck stage or

performance measures ofthe bottleneckmachines. Lean

manufacturing starts from well-deﬁned and accurate

performance measures. Many details of the machines

can be analyzed by data relating to material movements

from machine to machine, examples of which include

machine throughput, product lead time, and the work-

in-process (WIP) for each processing stage. Sometimes

they also provide beneﬁts for engineering analysis for

the improvement of quality control. The performance

of the IAMHS can also be measured and improved by

using these historical data. A new algorithm under test

can be easily tracked to assess how it performs in an ac-

tual application. Since there are many data transactions,

summarized tables are sometimes used for long-term

analysis. Data-mining approaches are helpful in design-

ing these tables.

AS/RS #2 MMS AGVS #2 AS/RS #3

Move request #1

Pick-up report #1

Job completion report #2

Port status change request #2

Port status change request #3

Job completion report #3

Job assign report #1

Move request #2

Move request #3

Job completion report #1

Port status change #1

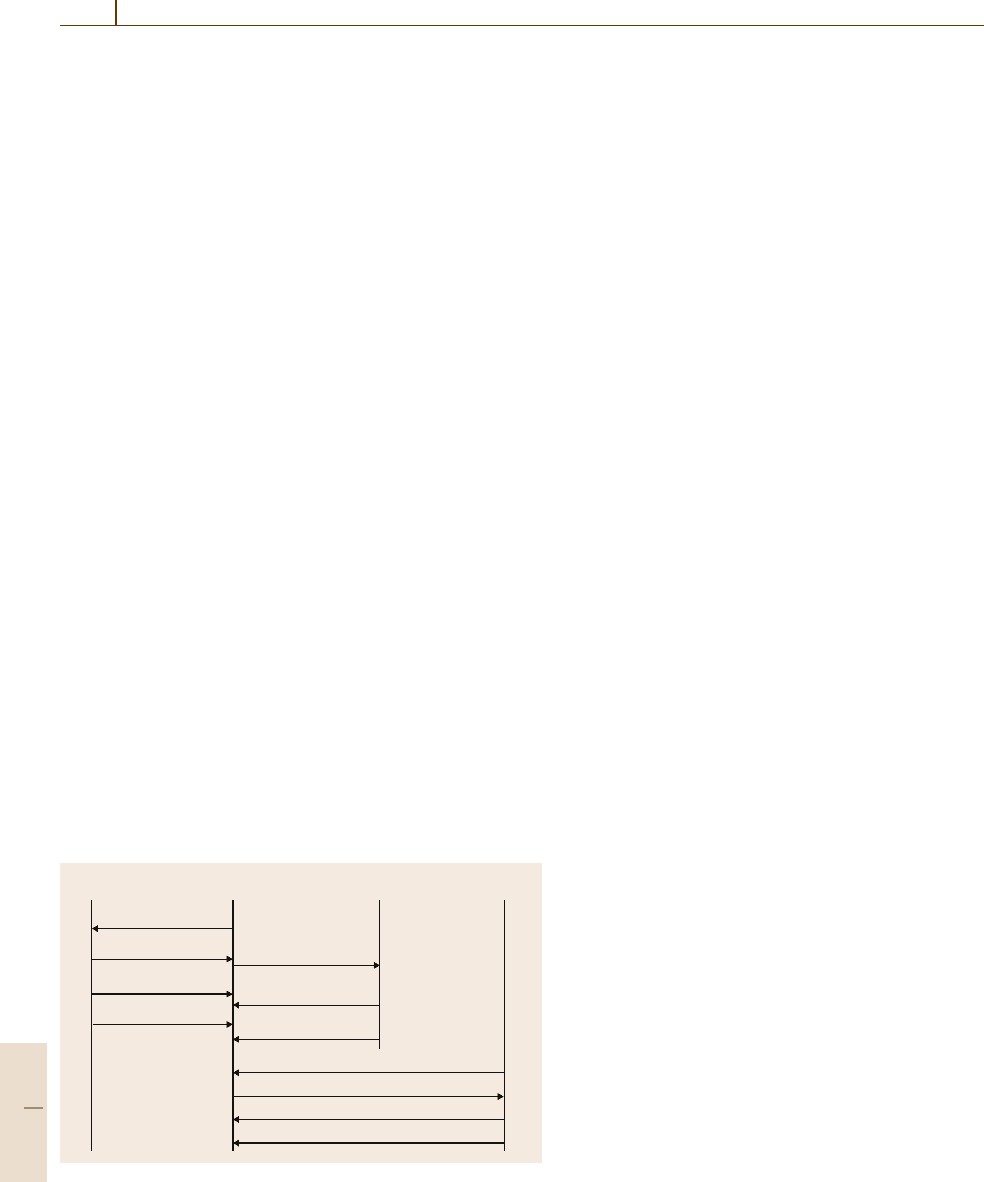
Fig. 55.7 Message sequence for a simple transfer command

Another important task of the MMS is the path

management function, which controls a sequence of

transportation jobs. Let us consider the following sim-

ple transfer request as an example. A transfer request

is sent to the MMS from the dispatching module to

move a unit load from a rack in AS/RS #2 to AS/RS #3

through AGVS #2 in Fig.55.5. Figure 55.7 shows

a message sequence illustrating communication be-

tween the MMS and AS/RS controllers involved in this

transfer, and between the MMS and AGV controller.

A few more messages might be used in actual systems.

As seen in the ﬁgure, although this is a relatively sim-

ple transferring task, more than 13 messages are used

to complete the task. First, transfer request #1 is trig-

gered by the MMS (it can be triggered by either the

dispatching module or a procedure of the MMS itself).

This request message transmits the source location as

AS/RS #2, the destination as the unload port of the

AS/RS, and the unit load identity to the AS/RS con-

troller #2. If there are other high-level systems such as

a WMS or MES,theMMS will send additional mes-

sages to these systems. In this case, the status of the

unit load possibly needs to be updated from Waiting to

Busy or Transferring for the WMS and MES.Tosend

this message to AS/RS controller #2, the MMS has to

make at least two major decisions: it has to select an

unload port among several idle ports, and to determine

to which among the many other AMHSs this message

should be sent. For the former decision, the closest idle

port to the next destination (i.e., AGVS #2) is selected

basedontheMMS algorithm. After receiving the trans-

fer request from the MMS, AS/RS controller #2 will put

the job into its queue, if it is performing other tasks. If it

is its turn, the controller will send the job assign report

to the MMS so that it triggers another transfer request

command toAGV controller #2.This transfercommand

could be sent later after the job completion message

from the AS/RS controller #2 has been received; how-

ever, by sending before the completion message, it can

synchronize the transfer activities of two systems and

thereby reduce the waiting time of the unit load for the

vehicle at the unload port of AS

/RS #2. The explanation

of the rest of the messages in the ﬁgure is omitted.

The MMS integrates not only systems but also

human operators in the system environment. A user

interface (UI) plays a major role in this integration. Op-

erators canmonitor thenumber of AMHSs using the UI.

Also, parameters to control an individual AMHS and

IAMHS are changed through the UI. Another important

function provided is reporting. Various reports can be

queried directly from the database of the MMS.

Part F 55.2

Material Handling Automation in Production and Warehouse Systems 55.3 Advanced Technologies 969

55.3 Advanced Technologies

This section surveys advanced technologies enabling

the IAMHS to achieve the high-level MHA. First, the

IIT utilizing wireless devices will be reviewed, then the

focus will move onto design and control issues of the

MHA. A wide range of methodologies across artiﬁcial

intelligence (AI) and operations research (OR) tech-

niques have been adopted to solve challengingproblems

in design and control of MHA. The design and control

issues with AMHS types will be brieﬂy described in-

cluding different points of interest. The review focuses

on the technical issues of the MMS, which is the most

important element of the IAMHS. Finally, AI and OR

techniques are compared according to several criteria in

MHA.

55.3.1 Information Interface Technology

(IIT) with Wireless Technology

Beneﬁts of wireless communication systems include

mobility, installation ﬂexibility, and scalability. Ap-

plications of the wireless communication used for

MHA are radiofrequency identiﬁcation (RFID), wire-

less local-area network (LAN) (i.e., Ethernet), and

wireless input/output (I/O). The wireless sensor net-

work has also great potential for many applications of

the MHA to collect data or form a closed-loop control

system.

Radiofrequency Identiﬁcation (RFID)

RFID enhances information tracking with a wide va-

riety of applications for material handling [55.16]; for

example, it prevents loss of boxes and incorrect ship-

ping in a distribution center and reduces time for

reading tags in boxes or carriers on a manufactur-

ing shop ﬂoor. Its greatest advantages over barcode

systems are its long read range, ﬂexibility of locat-

ing tags in boxes, multitasking for reading many tags

at the same time, and robustness against damage. Fi-

nally, RFID systems increase the accuracy of data from

material handling systems and reduce time for data

collection. With more reliable and faster information

tracking, more sequential operations can be automated

and integrated without affecting system performance

or requiring human interventions. It also enables the

development of higher-level MHA in production and

warehouse systems.

An RFID system consists of tags and readers. An

RFID tag has two components, a semiconductor chip

and antenna, and there are basically two types of RFID

tags, passive and active tags, based on the source of

the power. A passive tag does not have a battery and

is powered by the backscattered RF signal from the

reader, while an active tag has a battery and is there-

fore more reliable. Although the read range of a tag

depends strongly on its power level, antenna, and fre-

quency, and the environment in which it is used, an

active tag can have a range of up to 30m or more while

a passive tag can be read reliably over a few meters.

In between these two types, there is a semiactive tag

that is powered by RF from the reader and consumes

power from a battery while communicating with the

reader. The lifetime of the battery is about 7years or

more. Another classiﬁcation of RFID tags is based on

the ability to write information to tags. Some tags are

classiﬁed as read-only and can be written only once

but read many times; these are generally passive tags.

Information can be written by both users and produc-

ers. There are also rewritable passive tags in which

the program can be rewritten by users. Most active

tags are rewritable. RFID readers send RF signals to

tags, receive signals from tags, and communicate with

a central system. Their functions varies from a simple

on/off check for data collection to control of a large

system. Popularly used tags are as large as an elec-

tronic card, being installed in a larger computer system

with network capability; however, they can be as small

as 0.05×0.05mm

, as shown in Fig. 55.10.Onthe

right-hand side of Fig.55.8, powder-type RFID chips

developed by Hitachi are compared with a human hair.

Fig. 55.8 Mu-chips and powder type RFID chips (courtesy of Hi-

tachi)

Part F 55.3

970 Part F Industrial Automation

These powder-type RFID tags are 64 times smaller than

those in current use (0.4×0.4mm

mu-chips, on the

left, produced by the same company), which can al-

ready be embedded into paper currency, gift certiﬁcates,

and identiﬁcation documents. For more information in

RFID see Chap.49.

Wireless LAN

A wireless LAN establishes a network environment by

using wireless devices instead of wired ones within

a limited space. One popular application that adopts

wireless LAN in MHA is AGV systems, which use it

for communication between vehicles and controllers.

Each vehicle has a network interface card (NIC)that

is connected to the wireless LAN. An access point is

a gateway to connect to a wired LAN and similar to

a LAN hub, connecting 25–50 vehicles within a range

of 20–150 m. The infrastructure network is always con-

nected to an access point, which connects the wired

LAN with the wireless LAN. In the infrastructure net-

work, the basic service set (BSS) is formed and acts

as a base station connecting all vehicles in the cell to

the LAN. BSSs that use nonoverlapping channels can

be part of an extended service set (ESS). The vehi-

cles within the ESS but in different BSSs are connected

through roaming. Lee and Lee [55.17] develop an in-

tegrated communication system that connects Proﬁbus

and IEEE 802.11, which are wired and wireless LAN

communication protocols, for a container terminal auto-

matedbyanAGV system.Using thisprotocol converter,

the wirelessLAN can beconnected tothe existing wired

ﬁeldbus for soft real-time data exchange that loses some

of its usefulness after a time limit.

Wireless I/O

A wireless I/O device is a small circuit card with an

antenna installed in a material handling system or its

controller; it can be used for both data-acquisition and

closed-loop control applications. It receives microwave

radio data from I/O points, and sends those data to

a central processing device such as a programmable

logic controller (PLC), data loggers, supervisory con-

trol, and data-acquisition system (SCADA), or a general

PC [55.18]. Since it does not use wireless LAN or

a ﬁeldbus, implementation is much easier than afor

wireless LAN. It can be simply regarded as removing

the necessity for wires; however, by itself, it offers many

advantages such as broader connectivity, increased mo-

bility and ﬂexibility, reduced installation time, and

reduced points of failures. One of the disadvantages of

wireless I/O is that, since it uses a relatively narrow

range of wireless signals, a smaller number of wire-

less I/Os can be used in a certain area. Therefore, as the

number of points in an area grows, a wireless or wired

LAN will become more appropriate.

Wireless Sensor Networks

Sensor networks [55.19] are currently limited to novel

systems. Many sensors, distributed in a system or

area, can be used to build a network for monitor-

ing a space shuttle, military equipment unit or nuclear

power plant. Wireless sensor networks conceptually use

small, smart, cheap sensors that consist of a sensing

module, a data-processing module, and communica-

tion components; however, conventional sensors can

also be used. The network is mainly used for mon-

itoring systems that requires highly autonomous and

intelligent decision-making in a dynamic and uncer-

tain environment. They have a great deal of potential

to be adopted in MHA even though few researchers

have studied these applications. There are two ar-

eas of wireless sensor network applications for the

MHA.

First, reliability is oftenvery important for the MHA

because, in a highly automated system, the failure of

an AMHS causes the breakdown of multiple machines

or a whole area operated by the system. This may be

more critical than the failure of an individual process-

ing tool in production systems. Therefore, monitoring

and diagnosing the AMHS lead to some important is-

sues; for instance, vibration sensors and optical sensors

attached to the crane of an AS/RS collaborate to de-

tect a potential problem that might cause positioning

or more critical errors. By detecting the problem before

the AS/RS actually breaks down, engineers can recog-

nize the problem more precisely and prepare required

parts and tools in advance; hence, repair time can be

signiﬁcantly reduced.

Second, most AMHSs use a closed feedback sys-

tem that controls the system based on feedback from

component systems or sensors. Walker et al. [55.20]

studied a method to control an industrial robot that han-

dles ﬂexible materials such as wires and rubber hoses. It

utilizes feedback from sensor network cameras to pre-

dict the motion of the robot with the better vision. Since

the feedback can be created from many different points

such as grasps, paths, and goal points, it reduces blind

spots of unpredictable motions and greatly enhances

control precision. Chapter 20 provides additional infor-

mation on sensor networks.

Part F 55.3

Material Handling Automation in Production and Warehouse Systems 55.3 Advanced Technologies 971

Table 55.1 Design issues and related studies on MHA

Reference AMHS type Design issue Criteria Solution approach

Cho and Egbelu [55.21] IAMHS MHS equipment Qualitative factors, Fuzzy logic and

selection problem equipment variety knowledge-based rule

(minimizing)

Nadoli and IAMHS Design and Design lead time Expert system,

Rangaswami [55.22] modeling for a new computer simulation

semiconductor fab

Jimenez et al. [55.23] IAMHS Performance Delivery time, Computer simulation

evaluation of AMHS transport time,

throughput

Huang et al. [55.24] General Location of MHS Total distance, Lagrangian relaxation

MHS ﬁxed cost of MHS and heuristic method

Jang et al. [55.25] AS/RS Estimation of AS/RS Delivery rate, Queuing network

performance in-process inventory model

Lee et al. [55.26] AS/RS Optimal design of Space utilization Modular cells,

rack structure with (lost space) heuristic

various sized cells

Ting and Tanchoco AGV Location of the Total rectilinear MIP

[55.27] central path distance

Gaskins and Tanchoco AGV Guide path design: Total ﬂow distance Integer programming,

[55.28] direction of path heuristic

segments

Tanchoco and Sinriech AGV Guide path design: Total ﬂow distance Integer programming

[55.29] optimal design of

a single-loop

Bozer and Srinivasan AGV Guide path design: Balanced workload Integer programming,

[55.30] tandem guide path set partition

Caricato and Grieco AGV Guide path design Flow distance, Simulated annealing

[55.31] computation time

Nazzal and McGinnis AGV Estimation of Vehicle utilization, Queuing network

[55.32] performance blocking time, model

measures empty vehicle

interarrival time

Vis et al. [55.33] AGV Estimation of the Service level Network ﬂow

number of vehicles (waiting time)

55.3.2 Design Methodologies for MHA

MHA design studies largely deal with strategic

decision-making, which includes optimal selection of

automated material handling equipment, locating stor-

age and vehicle paths for new facility planning, rack

design for AS/RSs, ﬂow path design for AGV sys-

tems, and capacity estimation of the system. Table 55.1

brieﬂy summarizes studies related to design issues. The

MHA design problem is sometimes closely related to

the layout design problem in that both consider issues

at a very early stage of system implementation. Also,

they share performance measures in many areas. Pe-

ters and Yang [55.34] integrate these two methods into

Part F 55.3

972 Part F Industrial Automation

a single procedure using the space-ﬁlling curve (SFC)

method. Ting and Tanchoco [55.27] propose a new lay-

out design method for a semiconductor fab. They use

an integer programming model to determine the optimal

location of the AGV track. Chung and Jang [55.35] also

suggest a new layout alternative called integrated room

layout for better material handling in a semiconductor

fab and scrutinize the beneﬁts of the layout compared

with existing layout alternatives in the industry using

qualitative and quantitative analysis.

One of the difﬁculties in design of large-scale

IAMHSs is estimation of system capacity. Although

computer simulation has been used, its feedback cycle

from modeling to results analysisis very slow for a large

problem, which is an issue as timing of the solution

is sometimes very important. Also, a simple determin-

istic analysis using from–to charts of material ﬂows

cannot provide a precise estimation of variances in the

system. As an alternative approach studied for capac-

ity analysis, the queuing network approach shows good

performance [55.32]. Rembold and Tanchoco [55.36]

explore a framework that evaluates and improves a se-

quence of modeling tasks for material ﬂow systems.

They aim to develop a more fundamental solution to

the problems while encountered while designing an

IAMHS. The framework addresses the following ques-

tions of designers: selection of the software application

for solving a problem, organizing the data sets required

for the design, incorporation of the design into parts

that cannot be automated, and diagnosing problems in

material ﬂow systems. Those authors use an open archi-

tecture for the framework, since advance identiﬁcation

of all factors and cases for evaluation and redesign of

the material ﬂow processes are limited. With the open

architecture for the framework, users can easily ﬁnd

their own methods by incorporating ad hoc situations

into the framework.

55.3.3 Control Methodologies for MHA

Extensive research has been performed on the control

of the AMHS. Especially, AGV control problems have

beneﬁted from strong research streams in academia and

the MHA industry, since AGVs have been popular for

use in many industries. Figure 55.9 shows an inter-

esting AGV design with many storage racks that is

used in a hospital. Recently, two well-organized liter-

ature surveys on the AGV system were published by

Vis [55.37], and by Le-Anh and De Koster [55.38]. One

of the characteristics of control algorithms of MHA

is that minimizing ﬂow distance in time is a dom-

Fig. 55.9 AGV used in a hospital (courtesy of Egemin)

inant criterion, among others. Other criteria such as

resource utilization, throughput, and load balance have

frequently been subgoals to achieve the minimum ﬂow

time. Necessity for a very short response time is an-

other characteristic of control algorithms for the MHA;

for example, a vehicle dispatch algorithm for the AGV

controller should respond within a few seconds or less,

otherwise the vehicle will have to wait for a job com-

mand on the path. For a short response time, the time

horizon of the control algorithms is zero or very short,

because a longer time horizon often causes an explo-

sion of the search space. The minimum control horizon

also helps to yield a reliable solution because uncer-

tain parameters will be used less. If a control algorithm

malfunctions, the result will be more serious than just

a performance drop. It sometimes causes a detrimental

failure in the shop ﬂoor. Hence, a conservative approach

tends to be used in real applications.

A big challenge in AGV control problems is that

users want to use a larger loop with many vehicles in or-

der to reduce transportation time and investment. AGV

systems implemented earlier generally used a modular

structure to avoid heavy load on one AGV loop and had

many loops, with a maximum of about ﬁve vehicles in

a loop; however, these days, a large loop with a maxi-

mum about 40 vehicles is used. Therefore, the vehicle

dispatch, scheduling, routing, and deadlock avoidance

problems are becoming more complicated and impor-

tant. Table 55.2 summarizes control issues and their

studies in the MHA.

Part F 55.3

Material Handling Automation in Production and Warehouse Systems 55.3 Advanced Technologies 973

Table 55.2 Control issues and related studies on MHA

Researchers AMHS type Control issue Criteria Solution approach

Dotoli and Fanti [55.39] IAMHS Integrated AS/RS and Throughput, Colored Petri nets

RGV control computation time

Mahajan et al. [55.40] AS/RS Job sequencing Throughput Heuristic

(nearest neighborhood)

Lin and Tsao [55.8] AS/RS Crane scheduling for Total fulﬁllment time Heuristic

batch job in CIM of batch (dynamic availability

environment oriented controller)

Lee et al. [55.41] AS/RS Rack assignment for Expected travel time Heuristic (storage

cargo terminals reservation policy),

stochastic demand stochastic

Chetty and Reddy [55.42] AS/RS Job sequencing 10 criteria (mean ﬂow Genetic algorithm

time, mean waiting

time, min/max

completion time, etc.)

Sinriech and Palni [55.43] AGV Vehicle scheduling Optimality of MIP, heuristic (branch

scheduling solution and bound)

Correa et al. [55.44] AGV Vehicle scheduling Solution time, MIP and CP hybrid

job processing time method

Jang et al. [55.45] AGV Vehicle routing in AGV utilization, Heuristic, look-ahead

clean bay WIP level control procedure

Koo et al. [55.46] AGV Vehicle dispatching Production Heuristic, bottleneck-

throughput, lead time machine ﬁrst

Kim et al. [55.47] AGV Vehicle dispatching Production throughput Heuristic

in ﬂoor shop (balanced work load)

Jeong and Randhawa [55.48] AGV Vehicle dispatching Vehicle travel time, Heuristics, multi-

blocking time, WIP attribute dispatching

Moorthy et al. [55.49] AGV Deadlock avoidance Number of AGVsin Heuristic,

in large-scale AGVS a loop, state prediction

(cycle deadlock) number deadlocks

Bruno et al. [55.50] AGV Empty vehicle Response time Heuristic (location

parking model (MIP)and

shortest path algorithm)

IAMHS Research

Researchers recently started to study complicated is-

sues of the IAMHS. A major concern is routing

strategies from source to destination location in a com-

plicated IAMHS, in which there are multiple routes

from one location to the others. The routes consist

of not only physical paths such as an AGV path or

conveyor track but also AMHS themselves, such as

AS/RSs, AGVSs, and buffer stations. Practical appli-

cations generally store predetermined static shortest

routes in a database for all pairs of source locations and

destinations; however, when the number of components

increases, maintenance problems for the parameters in-

volved become much more difﬁcult since there are too

many combinations of nodes. The shortest-distance al-

gorithm using graph theory with an adjacency matrix

might be a better approach.

A new concept called ﬂow diversion is proposed

to determine dynamic routing based on the load rate

of the routes in automated shipment handling sys-

tems by Cheung et al. [55.51]. The authors utilize the

multicommodity ﬂow models using linear program-

ming (LP) to solve this problem. In this model, the

transfer time for a route is a function of the loads as-

signed to all pairs of unit loads in the system, which

generates a nonlinear function in the objective func-

Part F 55.3

974 Part F Industrial Automation

tion; those authors transform this nonlinear function

to a piecewise-linear function to make the problem

tractable. Lau and Zhao [55.4] study a joint job schedul-

ing problem for the automated air cargo terminal at

Hong Kong, which is mainly composed of AGV sys-

tems, AS/RSs, cargo hoists, and conveyors. In the

model, activities between different AMHSs are trig-

gered by communication between the systems. The

scheduling algorithm constructs a cooperative sequen-

tial job served by different AMHSs, employing the

maximum matching algorithm of the bipartite graph.

A task for an AGV is assigned or matched to an stacker

crane (SC) to reduce the SC delay time. A similar prob-

lem is solved by Meersmans and Wagelmans [55.5].

Their research focuses on the scheduling problem of the

IAMHS in seaport terminals employing a local beam

search algorithm. The nodes explored in the search al-

gorithm are represented by a sequence of container IDs

to be processed by different AMHSs, and the nodes in

branches are cutbased onthe beam widthdetermined by

an evaluation function. Those authors prove that there

existsan optimalsequence of tasks forone AMHS when

the sequence is assigned to the other AMHS.

Sujono and Lashkari [55.52] study another inte-

grating method allocating a part type to a processing

machine and material handling (MH) equipment type

simultaneously in a ﬂexible manufacturing system

(FMS). In that research, there are nine different types

of the material handling systems in the experimental

model. The method improves the algorithms proposed

by Paulo et al. [55.53]andLashkari et al. [55.54]and

uses a 0/1 mixed integer programming model. Two ob-

jective functions are modeled: one minimizes operating

costs related to machine operations, setup, and MH

operations; the other maximizes the compatibility of

the part types using MH equipment types. To measure

compatibility, parameters are quantiﬁed from the sub-

jective factors deﬁned by Ayres [55.55]. Some of the

constraints are: balance equations between parts and

process plans, machines and process plan, processing

machines, and MH equipment types. The other impor-

tant constraint sets are capacity constraints: the total

load of the allocated tasks for an MH equipment type

cannot exceed its capacity, and a machine cannot be

allocated more than its capacity. A test problem con-

sisting of 1356 constraints and 3036 binary variables

was solved in about 9.2s by using LINGO in a Pen-

tium 4 PC. Since this model considers many details of

the practical factors in the FMS, and showed a suc-

cessful calculation result, it can be used for many other

practical applications.

In addition to the examples shown above, large-

scale optimization problems such as the vehicle routing

problem (VRP), vehicle scheduling problem (VSP), and

integrated scheduling problem of IAMHS

with con-

sideration of processing machines have been modeled

to increase MHA efﬁciency. However, to be used for

actual applications and thereby achieve a higher-level

MHA, shorter computation times are urgently required.

In a complicated IAMHS, integrating software pack-

ages such as the MMS need sophisticated algorithms;

however, it also needs high reliability in a dynamic en-

vironment. For most tasks, real-time decision-making

that requires response times within a few seconds is

a precondition for IAMHS algorithms.

MMS-related Issues

The MMS is a key component to integrate different

AMHSsinanIAMHS. Destination allocation, routing

algorithm, and prioritizing algorithm are essential roles

of the MMS, among others. Graph theory is popularly

used to represent components and relationships in the

IAMHS.InFig.55.6, nodes represent the AMHSsand

their subcomponents, such as load/unload ports. Edges

represent the connection and distance between nodes.

As mentioned above, this graph is stored in database

tables using the adjacency and incidence matrices. The

shortest-path algorithm isthe mostimportant and funda-

mental algorithmfor an MMS since it is usedfor several

purposes in the system such as destination assignment

and best routing determination. Dijkstra’s algorithm is

popularly used [55.56]. The Bellman–Ford algorithm

can be used if there are negative weights of the edges.

To determine the ﬁnal destination of a unit load,

the MMS has to evaluate various factors on the same

scale. More speciﬁcally, to determine an AS/RS as the

ﬁnal destination among several alternatives, the shortest

distance is generally the most important criterion; how-

ever, the full rates of the AS/RSs are sometimes also

important to make the loads balanced between different

AS/RSs. There are two applicable ways to standard-

ize different scales of factors on the same scale. First,

different weight values can be applied for each factor

to ﬁnd the best alternatives. Second, a priority and its

threshold value can be givento each factor, and the most

important alternativeis selectedif it is within the thresh-

old, otherwise the next alternative will be considered.

Determining the best route from a source to desti-

nation location via several AMHSs is relatively simple

when compared with the vehicle routing problem(VRP)

or vehicle schedulingproblem (VSP), becausethe graph

generally has a smaller number of nodes than those of

Part F 55.3