Невзоров В.Н., Сугак Е.В. Надежность машин и оборудования. Часть 2

Подождите немного. Документ загружается.

131

( )

t a

* *

, , , , , ,= +

= +

= = × =G G G1

161 1

161 134 1610892 144

ãäå G(1,34) » 0,892 - çíà÷åíèå ãàììà-ôóíêöèè (ñì.ïðèë.I);

- âåðîÿòíîñòè áåçîòêàçíîé ðàáîòû p(t) çà íàðàáîòêó t = 1,0 òûñ.êì

()

p t

* , exp

exp

, ;

= = -

= -

=10

161

0775

- èíòåíñèâíîñòè îòêàçîâ l(t) çà íàðàáîòêó t = 1,0 òûñ.êì

()

, .

= × = × =

- -1

291

161

1 0729

Ïðèìåð 8.11 [8] Ïî ðåçóëüòàòàì ðàñ÷åòîâ ïðèìåðà 8.5 äëÿ ðàñïðåäåëåíèÿ Âåéáóëëà

ñ ïàðàìåòðàìè a*=1,60 è b*=3 îöåíêà ñðåäíåãî ðåñóðñà ïî ôîðìóëå òàáë.8.7:

( )

t a

* *

, , , , , ,,= +

= × +

= × = × =G G G1

160 1

161 133 1600893 143

ãäå G(1,34) » 0,893 - çíà÷åíèå ãàììà-ôóíêöèè (ñì.ïðèë.I).

Ïðèìåð 8.12 [13]. Ïî äàííûì è ðåçóëüòàòàì ðàñ÷åòîâ ïðèìåðà 8.6 äëÿ ðàñïðåäåëå-

íèÿ Âåéáóëëà îïðåäåëèòü ñðåäíþþ íàðàáîòêó äî îòêàçà è âåðîÿòíîñòü áåçîòêàçíîé ðà-

áîòû çà íàðàáîòêó 100 ÷.

Ïî ôîðìóëàì òàáë.8.7 ïðè a*=134,29 è b*=3,06 îöåíêè ñðåäíåé íàðàáîòêè è âåðî-

ÿòíîñòè áåçîòêàçíîé ðàáîòû çà íàðàáîòêó 100 ÷

( )

t a

* *

, , , , ,,= +

= × +

= × = × =G G G1

13429 1

206

13429 1485 134290 11885885

()

p t

* , exp

exp

= = -

= -

=10

100

13429

058

206

ãäå G(1,34) » 0,893 - çíà÷åíèå ãàììà-ôóíêöèè (ñì.ïðèë.I).

8.2.4. Выявление закона выборочного распределения

Âèä ôóíêöèè ðàñïðåäåëåíèÿ íàðàáîòêè ÷àñòî çàðàíåå íå èçâåñòåí è

äîëæåí îïðåäåëÿòüñÿ ïî ýìïèðè÷åñêèì äàííûì. Ïðåäïîëîæåíèå (ñòàòèñ-

òè÷åñêàÿ ãèïîòåçà) î âèäå ôóíêöèè ðàñïðåäåëåíèÿ F(t) íàðàáîòêè t ìî-

æåò áûòü ñäåëàíî èç àíàëèçà ýêñïåðèìåíòàëüíûõ äàííûõ èëè êàêèõ-ëèáî

äîïîëíèòåëüíûõ ñîîáðàæåíèé (íàïðèìåð, èç ôèçè÷åñêîé ñóùíîñòè ïðîöåñ-

ñîâ è ÿâëåíèé).

Â îáùåì ñëó÷àå çàäà÷à âûÿâëåíèÿ çàêîíà âûáîðî÷íîãî ðàñïðåäåëåíèÿ

ñîñòîèò â âûáîðå íà îñíîâàíèè âûáîðî÷íîé ñîâîêóïíîñòè çíà÷åíèé ñëó-

÷àéíîé âåëè÷èíû îáúåìîì n íàèáîëåå ïîäõîäÿùåãî òåîðåòè÷åñêîãî ðàñ-

ïðåäåëåíèÿ è îïðåäåëåíèè õàðàêòåðèñòèê ýòîãî ðàñïðåäåëåíèÿ. Òåîðåòè÷å-

ñêîå ðàñïðåäåëåíèå äîëæíî íàèëó÷øèì îáðàçîì àïïðîêñèìèðîâàòü ýìïè-

ðè÷åñêîå âûáîðî÷íîå ðàñïðåäåëåíèå.

Äëÿ òî÷íîãî îïðåäåëåíèÿ âèäà âûáîðî÷íîãî ðàñïðåäåëåíèÿ íàðàáîòêè

ïðè îïðåäåëèòåëüíûõ èñïûòàíèÿõ íóæíî äàòü äîðàáîòàòü äî îòêàçà âñåì

èçäåëèÿì â âûáîðêå. Ýòî âîçìîæíî òîëüêî ïðè ïëàíå èñïûòàíèé [NUN]. Â

îñòàëüíûõ ñëó÷àÿõ íàèáîëüøèå çíà÷åíèÿ ñëó÷àéíûõ íàðàáîòîê íå áóäóò

çàôèêñèðîâàíû, òàê ÷òî âûáîðî÷íàÿ ñîâîêóïíîñòü îêàæåòñÿ èñêàæåííîé,

÷òî èñêàçèò è âûÿâëåíèå çàêîíà ðàñïðåäåëåíèÿ. Ýòî îáñòîÿòåëüñòâî íåîá-

õîäèìî ó÷èòûâàòü ïðè âûáîðå ïëàíà îïðåäåëèòåëüíûõ èñïûòàíèé.

132

Âûáîð àïïðîêñèìèðóþùåãî ðàñïðåäåëåíèÿ äëÿ âûáîðî÷íîé ñîâîêóïíî-

ñòè ñëó÷àéíîé íàðàáîòêè ìîæåò ïðîèçâîäèòüñÿ ëèáî ïî âèäó ñòàòèñòè÷å-

ñêîãî ðàñïðåäåëåíèÿ, ëèáî ãðàôè÷åñêèì ìåòîäîì ñ èñïîëüçîâàíèåì âåðî-

ÿòíîñòíûõ êîîðäèíàòíûõ ñåòîê.

Òèï ôóíêöèè ðàñïðåäåëåíèÿ ïðè àíàëèçå ýêñïåðèìåíòàëüíûõ äàííûõ

îáû÷íî óñòàíàâëèâàåòñÿ ïî âíåøíåìó âèäó ñòàòèñòè÷åñêèõ ãðàôèêîâ - ãèñ-

òîãðàììû, ïîñòðîåííîé íà íåáîëüøèõ èíòåðâàëàõ èçìåíåíèÿ ñëó÷àéíîé

âåëè÷èíû, èëè àïïðîêñèìèðóþùåé êðèâîé.

Äëÿ ïîñòðîåíèÿ ñòàòèñòè÷åñêèõ ãðàôèêîâ âûáîðî÷íàÿ ñîâîêóïíîñòü

,...,t

) ïðåîáðàçóåòñÿ â âàðèàöèîííûé ðÿä (t

(1)

(2)

,...,t

(n)

). Ïðè ýòîì

ñëó÷àéíûå çíà÷åíèÿ t

ðàíæèðóþòñÿ, ò.å. óïîðÿäî÷èâàþòñÿ â ïîðÿäêå âîç-

ðàñòàíèÿ (âêëþ÷àÿ îäèíàêîâûå), ò.å. t

(i+1)

³ t

(i)

. Ðàçíîñòü ìàêñèìàëüíîãî è

ìèíèìàëüíîãî çíà÷åíèé âàðèàöèîííîãî ðÿäà - ðàçìàõ âàðüèðîâàíèÿ

= t

(n)

-t

(1)

(8.39)

ðàçáèâàåòñÿ íà k äîñòàòî÷íî ìàëûõ (îáû÷íî îäèíàêîâûõ) èíòåðâàëîâ

Dt=R

/k (ãðàíèöû èíòåðâàëîâ óäîáíî ïðèâÿçûâàòü ê öåëûì èëè êðóãëûì

çíà÷åíèÿì ïåðåìåííîé t).

×èñëî èíòåðâàëîâ k è èõ âåëè÷èíà Dt

äîëæíû óäîâëåòâîðÿòü ïðîòèâî-

ðå÷èâûì òðåáîâàíèÿì: ÷åì áîëüøå çíà÷åíèå k, òåì ïëàâíåå áóäåò ñòàòè-

ñòè÷åñêèé ãðàôèê, îäíàêî, åñëè èíòåðâàëû áóäóò î÷åíü ìàëû, òî íåêîòî-

ðûå èç íèõ ìîãóò îêàçàòüñÿ ïóñòûìè è ïëàâíîñòü ãðàôèêà òàêæå íå áóäåò

äîñòèãíóòà. Ðàçìåð èíòåðâàëîâ âûáèðàåòñÿ òàêèì, ÷òîáû â êàæäûé èíòåð-

âàë ïîïàäàëî â ñðåäíåì íå ìåíåå 3-5 çíà÷åíèé t

(i)

, à ÷èñëî èíòåðâàëîâ k

áûëî íå ìåíåå 5-10. Ðåêîìåíäóåòñÿ, ÷òîáû äëÿ ïåðâîãî è ïîñëåäíåãî èí-

òåðâàëîâ âûïîëíÿëîñü íåðàâåíñòâî np

*³1, äëÿ îñòàëüíûõ - np

*³5 (îáû÷íî

5£k£20). Ìîæíî òàêæå âîñïîëüçîâàòüñÿ ñîîòíîøåíèÿìè: k»1+3,21×ln(n)

[19,20], k»1+3,3×lg(n) [9,18] èëè k»4×[0,75(n-1)

]

0,2

(ïðè n>200) [21-23]. Åñëè

çíà÷åíèÿ t

(i)

â îñíîâíîì ñîñðåäîòî÷åíû â îäíîé îáëàñòè ðàçìàõà âàðüèðî-

âàíèÿ, ìîæíî ñäåëàòü èíòåðâàëû íåîäèíàêîâûìè: ìàëûìè â îáëàñòè ãðóï-

ïèðîâàíèÿ t

(i)

è áîëüøèìè çà åå ïðåäåëàìè.

Äëÿ ãðóïïèðîâàíèÿ ïî èíòåðâàëàì ïîäñ÷èòûâàåòñÿ êîëè÷åñòâî ÷ëåíîâ

âàðèàöèîííîãî ðÿäà Dn

(j=1,2,...,k), ïîïàäàþùèõ â êàæäûé èíòåðâàë (åñëè

íåêîòîðûå çíà÷åíèÿ ïîïàäàþò íà ãðàíèöû èíòåðâàëîâ, òî îíè çàñ÷èòûâà-

þòñÿ ïîðîâíó â êàæäûé èç íèõ). Âûñîòà ïðÿìîóãîëüíèêà â ãèñòîãðàììå

ïðîïîðöèîíàëüíà ñòàòèñòè÷åñêîé ÷àñòîòå â èíòåðâàëå

t n

j j

= =

D D

. (8.40)

èëè (ïðè îäèíàêîâûõ èíòåðâàëàõ Dt

) âåðîÿòíîñòè ïîïàäàíèÿ ñëó÷àéíîé

âåëè÷èíû â j-é èíòåðâàë

j j

= =

. (8.41)

133

à)

á)

â)

(1)

(2)

...

1/n

(

)

(

)

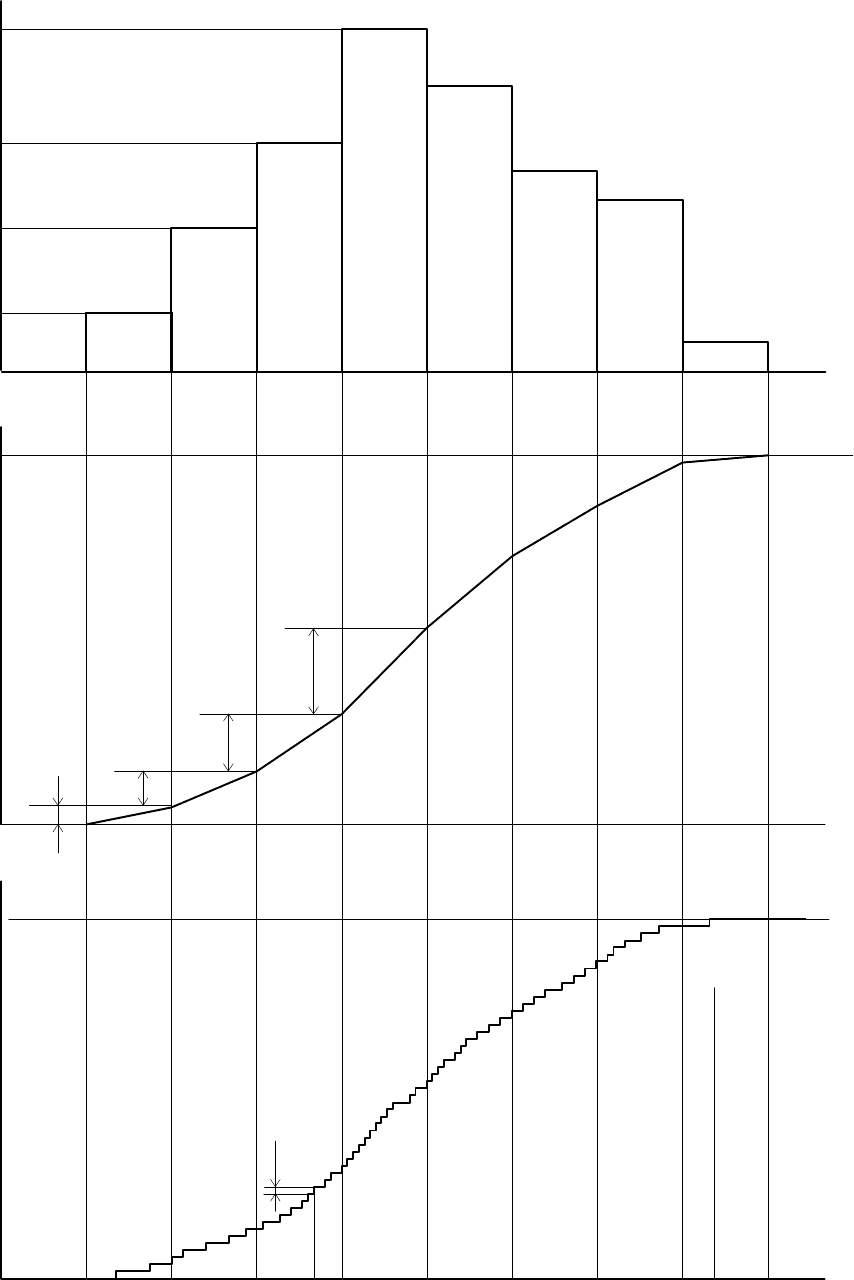
Ðèñ.8.4. Âûÿâëåíèå çàêîíà âûáîðî÷íîãî ðàñïðåäåëåíèÿ:

à - ãèñòîãðàììà íàðàáîòêè, á - ñòàòèñòè÷åñêàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ,

íåñãðóïïèðîâàííàÿ ñò

àòèñòè÷åñêàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ.

134

Ñòóïåí÷àòûé ãðàôèê f

*(t) (ðèñ.8.4à) îáðàçóåò ãèñòîãðàììó íàðàáîòêè.

Ñòàòèñòè÷åñêèå îöåíêè õàðàêòåðèñòèê ðàñïðåäåëåíèÿ îïðåäåëÿþòñÿ ïî

ôîðìóëàì (8.4)-(8.7), êîòîðûå äëÿ ãèñòîãðàììû ìîæíî ïðåäñòàâèòü â âèäå:

() () ()

[ ]

M t tp D t t M t p

* , *

* *

= = -

= =

å å

* , (8.42)

ãäå`t

- ñåðåäèíà j-ãî èíòåðâàëà.

Âåëè÷èíó ñòàòèñòè÷åñêîé ôóíêöèè ðàñïðåäåëåíèÿ F

*(t) â âåðõíåé

òî÷êå j-ãî èíòåðâàëà ìîæíî îïðåäåëèòü êàê íàêîïëåííóþ ÷àñòîòó

( )

Ft p

j j i

* max *

= = =

å å å

D , (8.43)

ò.å. â âèäå îòíîñèòåëüíîé ñóììû êîëè÷åñòâà çíà÷åíèé âàðèàöèîííîãî ðÿäà,

ìåíüøèõ t

max

. Ñîñåäíèå òî÷êè íà ãðàôèêå F

*(t) ñîåäèíÿþòñÿ ïðÿìûìè

îòðåçêàìè (ðèñ.8.4á).

Íå ïðèáåãàÿ ê ãðóïïèðîâàíèþ ìîæíî ïîñòðîèòü íåñãðóïïèðîâàííóþ

ñòàòèñòè÷åñêóþ ôóíêöèþ ðàñïðåäåëåíèÿ. Èíòåãðàëüíàÿ ôóíêöèÿ ðàñ-

ïðåäåëåíèÿ F(t) â íåêîòîðîé òî÷êå t - âåðîÿòíîñòü òîãî, ÷òî ñëó÷àéíàÿ íà-

ðàáîòêà ïðèìåò çíà÷åíèå ìåíüøåå èëè ðàâíîå t. Î÷åâèäíî, ñòàòèñòè÷åñêîé

îöåíêîé ýòîé âåðîÿòíîñòè ÿâëÿåòñÿ îòíîøåíèå êîëè÷åñòâà çíà÷åíèé âà-

ðèàöèîííîãî ðÿäà, ìåíüøèõ t, ê îáùåìó ÷èñëó çíà÷åíèé, ò.å.

F*(t) = n(t

£t)/n. (8.44)

Ñëåäîâàòåëüíî, íåñãðóïïèðîâàííàÿ ôóíêöèÿ F*(t) ñòóïåí÷àòî óâåëè÷è-

âàåòñÿ íà âåëè÷èíó 1/n ïðè ïåðåõîäå ÷åðåç êàæäîå çíà÷åíèå âàðèàöèîí-

íîãî ðÿäà t

(i)

è îñòàåòñÿ íà ýòîì óðîâíå äî ñëåäóþùåãî çíà÷åíèÿ t

(i+1)

(ðèñ.8.4â). Íåñãðóïïèðîâàííàÿ ôóíêöèÿ áîëåå òî÷íî îòîáðàæàåò âûáîðî÷-

íóþ ñîâîêóïíîñòü ïî ñðàâíåíèþ ñî ñãðóïïèðîâàííîé.

Ñðàâíèâàÿ âèä ïîëó÷åííûõ ñòàòèñòè÷åñêèõ ãðàôèêîâ f*(t) èëè F*(t) ñ

âèäîì ãðàôèêîâ ïëîòíîñòè âåðîÿòíîñòè èëè èíòåãðàëüíîé ôóíêöèè òåîðå-

òè÷åñêèõ ðàñïðåäåëåíèé, âûáèðàåòñÿ íàèáîëåå ïîäõîäÿùèé çàêîí, äëÿ êî-

òîðîãî çàòåì ïðîèçâîäèòñÿ êîëè÷åñòâåííàÿ ïðîâåðêà ñîãëàñèÿ.

Ïðèìåð 8.13. Ïî ðåçóëüòàòàì èñïûòàíèé 50 îáúåêòîâ ïî ïëàíó [NUN] (òàáë.8.8)

îïðåäåëèòü âèä ðàñïðåäåëåíèÿ íàðàáîòêè.

Äëÿ îïðåäåëåíèÿ âèäà âûáîðî÷íîãî ðàñïðåäåëåíèÿ è îïðåäåëåíèÿ åãî ïàðàìåòðîâ

íåîáõîäèìî ïîñòðîèòü ãèñòîãðàììó. Ðàçíîñòü ìàêñèìàëüíîãî è ìèíèìàëüíîãî çíà÷åíèé

âàðèàöèîííîãî ðÿäà - ðàçìàõ âàðüèðîâàíèÿ (8.39) R

= 169,71-32,22=137,49. Ãðàíèöû

èíòåðâàëîâ óäîáíî ïðèâÿçàòü ê öåëûì çíà÷åíèÿì ïåðåìåííîé t ÷åðåç 20 ÷: 20, 40, 60,

80, 100, 120, 140, 160 è 180 ÷.

Ãðàíèöû èíòåðâàëîâ, êîëè÷åñòâî ÷ëåíîâ âàðèàöèîííîãî ðÿäà, ïîïàäàþùèõ â êàæäûé

èíòåðâàë Dn

(j=1,2,...,8) è ñòàòèñòè÷åñêàÿ ÷àñòîòà f

*=Dn

/(nDt

) ïðåäñòàâëåíû â

òàáë.8.9. Íà ðèñ.8.5à ïîêàçàíà ãèñòîãðàììà, ïîñòðîåííàÿ ïî ðåçóëüòàòàì ãðóïïèðîâàíèÿ.

Íà ðèñ.8.5á ïðåäñòàâëåí ãðàôèê ñòàòèñòè÷åñêîé ôóíêöèè ðàñïðåäåëåíèÿ F

*(t

max

çíà÷åíèÿ êîòîðîé (òàáë.8.9) äëÿ ïðàâûõ ãðàíèö èíòåðâàëîâ ðàññ÷èòàíû ïî ôîðìóëå

(8.43). Çíà÷åíèÿ íåñãðóïïèðîâàííîé ñòàòèñòè÷åñêîé ôóíêöèè ðàñïðåäåëåíèÿ (8.44)

ïðåäñòàâëåíû â òàáë.8.8 è ðèñ.8.5â.

Ïðèìåðíàÿ ñèììåòðè÷íîñòü ãèñòîãðàììû (ðèñ.8.4à) è âèä ãðàôèêîâ ôóíêöèè ðàñ-

ïðåäåëåíèÿ (ðèñ.8.5á è 8.5â) ïîçâîëÿåò ïðåäïîëîæèòü íîðìàëüíûé çàêîí ðàñïðåäåëå-

íèÿ. Ïî ôîðìóëàì (8.41) è (8.42) ïîëó÷àåì îöåíêè ìàòåìàòè÷åñêîãî îæèäàíèÿ, äèñïåð-

ñèè è ñðåäíåãî êâàäðàòè÷åñêîãî îòêëîíåíèÿ: m* = M*(t) » 98,8 ÷, s*

= D*(t) » 866,6

, s* » 29,4 ÷.

135

Òàáëèöà 8.8

РЕЗУЛЬТАТЫ ИСПЫТАНИЙ И ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

F*(t

)

, ìì

F(t

)

|F(t

)-F*(t

31,22

0,02

-2,054

1,409

-33,106

0,0192

0,0008

34,79

0,04

-1,751

5,522

-28,221

0,0250

0,0150

40,85

0,06

-1,555

12,514

-25,063

0,0383

0,0217

42,65

0,08

-1,405

14,593

-22,650

0,0433

0,0367

52,10

0,10

-1,282

25,494

-20,659

0,0780

0,0220

54,11

0,12

-1,175

27,823

-18,941

0,0876

0,0324

60,75

0,14

-1,080

35,479

-17,415

0,1254

0,0146

67,48

0,16

-0,994

43,244

-16,031

0,1741

0,0141

67,82

0,18

-0,915

43,633

-14,756

0,1768

0,0032

68,24

0,20

-0,842

44,125

-13,567

0,1803

0,0197

69,80

0,22

-0,772

45,921

-12,448

0,1933

0,0267

82,85

0,24

-0,706

60,979

-11,386

0,3235

0,0835

83,75

0,26

-0,643

62,014

-10,371

0,3337

0,0737

85,05

0,28

-0,583

63,519

-9,395

0,3486

0,0686

85,47

0,30

-0,524

64,001

-8,453

0,3535

0,0535

85,59

0,32

-0,468

64,140

-7,539

0,3549

0,0349

87,39

0,34

-0,412

66,215

-6,649

0,3760

0,0360

92,47

0,36

-0,358

72,079

-5,778

0,4375

0,0775

95,05

0,38

-0,305

75,056

-4,924

0,4695

0,0895

97,64

0,40

-0,253

78,048

-4,084

0,5018

0,1018

97,80

0,42

-0,202

78,236

-3,255

0,5038

0,0838

98,46

0,44

-0,151

78,994

-2,434

0,5120

0,0720

99,06

0,46

-0,100

79,681

-1,619

0,5194

0,0594

101,51

0,48

-0,050

82,511

-0,808

0,5499

0,0699

101,80

0,50

0,000

82,850

0,000

0,5535

0,0535

103,30

0,52

0,050

84,572

0,808

0,5719

0,0519

104,24

0,54

0,100

85,659

1,619

0,5834

0,0434

104,60

0,56

0,151

86,077

2,434

0,5878

0,0278

106,04

0,58

0,202

87,740

3,255

0,6052

0,0252

108,01

0,60

0,253

90,013

4,084

0,6287

0,0287

108,29

0,62

0,305

90,334

4,924

0,6320

0,0120

108,59

0,64

0,358

90,683

5,778

0,6356

0,0044

109,38

0,66

0,412

91,591

6,649

0,6448

0,0152

110,63

0,68

0,468

93,033

7,539

0,6592

0,0208

111,75

0,70

0,524

94,324

8,453

0,6719

0,0281

111,90

0,72

0,583

94,505

9,395

0,6737

0,0463

116,14

0,74

0,643

99,389

10,371

0,7199

0,0201

116,76

0,76

0,706

100,107

11,386

0,7264

0,0336

118,77

0,78

0,772

102,426

12,448

0,7469

0,0331

119,48

0,80

0,842

103,245

13,567

0,7539

0,0461

126,54

0,82

0,915

111,390

14,756

0,8179

0,0021

126,94

0,84

0,994

111,859

16,031

0,8212

0,0188

128,15

0,86

1,080

113,255

17,415

0,8310

0,0290

131,91

0,88

1,175

117,589

18,941

0,8589

0,0211

133,10

0,90

1,282

118,965

20,659

0,8671

0,0329

134,97

0,92

1,405

121,123

22,650

0,8792

0,0408

137,12

0,94

1,555

123,597

25,063

0,8921

0,0479

155,94

0,96

1,751

145,310

28,221

0,9661

0,0061

157,30

0,98

2,054

146,880

33,106

0,9692

0,0108

169,71

1,00

161,203

0,9880

0,0120

136

Âèä è ïàðàìåòðû ðàñïðåäåëåíèÿ ìîãóò áûòü òàêæå îïðåäåëåíû ãðàôè-

÷åñêèì ìåòîäîì ñ ïîìîùüþ âåðîÿòíîñòíûõ êîîðäèíàòíûõ ñåòîê ñ íåëè-

íåéíûì ìàñøòàáîì ïî êîîðäèíàòíûì îñÿì ïîñëå íàíåñåíèÿ íà íèõ ýêñïå-

ðèìåíòàëüíûõ äàííûõ (ïðèë.II) [24-26]. Òàê êàê ïðè èñïîëüçîâàíèè ãðàôè-

÷åñêîãî ìåòîäà äëÿ ëþáîãî ðàñïðåäåëåíèÿ ãðàôèê ôóíêöèè ðàñïðåäåëåíèÿ

ïðèîáðåòàåò âèä ïðÿìîé, òî äëÿ åå áîëåå òî÷íîãî ïîñòðîåíèÿ è îïðåäåëå-

íèÿ êîîðäèíàò òî÷åê ïåðåñå÷åíèÿ ñ îñÿìè è ïàðàìåòðîâ ðàñïðåäåëåíèÿ

ìîæíî âîñïîëüçîâàòüñÿ ìåòîäîì (ñïîñîáîì) íàèìåíüøèõ êâàäðàòîâ

(ïðèë.III).

Ïîñòðîåíèå ïî äàííûì ïðèâåäåííîãî ïðèìåðà ïîêàçûâàåò (ïðèë.II), ÷òî â âåðîÿòíîñò-

íûõ êîîðäèíàòàõ äëÿ íîðìàëüíîãî çàêîíà ðåçóëüòàòû èñïûòàíèé â âèäå òî÷åê ðàñïîëàãàþò-

ñÿ âäîëü ïðÿìîé ëèíèè, ÷òî ïîäòâåðæäàåò ïðàâèëüíîñòü âûáîðà çàêîíà ðàñïðåäåëåíèÿ.

Êîýôôèöèåíòû àïïðîêñèìèðóþùåãî ëèíåéíîãî óðàâíåíèÿ y =ax+b ìîãóò áûòü íàé-

äåíû ïî ôîðìóëàì ìåòîäà íàèìåíüøèõ êâàäðàòîâ (ïðèë.III). Ïîäñòàíîâêà çíà÷åíèé äëÿ

50 òî÷åê ïðèìåðà 8.13 è âû÷èñëåíèÿ (ñì.ïðèë.II) äàþò ïðèáëèæåííûå çíà÷åíèÿ ìàòå-

ìàòè÷åñêîãî îæèäàíèÿ è ñðåäíåãî êâàäðàòè÷åñêîãî îòêëîíåíèÿ íàðàáîòêè m » 97,44 ÷,

s » 31,95 ÷. Îêîí÷àòåëüíî ìîæíî ïðèíÿòü m = 97,5 ÷ è s = 32,0 ÷.

8.2.5. Проверка статистических гипотез

Ïîñëå âûáîðà òåîðåòè÷åñêîãî çàêîíà ðàñïðåäåëåíèÿ, íàèáîëåå áëèçêîãî

ê ñòàòèñòè÷åñêîìó, è îöåíêè åãî ïàðàìåòðîâ ïðîèçâîäèòñÿ êîëè÷åñòâåííàÿ

îöåíêà ñïðàâåäëèâîñòè àïïðîêñèìàöèè. Ïðîâåðêà ñòàòèñòè÷åñêèõ ãèïîòåç,

ò.å. ïðîâåðêà ñîîòâåòñòâèÿ çíà÷åíèé ñëó÷àéíîé âåëè÷èíû ïðåäïîëàãàåìîé

ôóíêöèè ðàñïðåäåëåíèÿ, îñóùåñòâëÿåòñÿ ñ ïîìîùüþ êðèòåðèåâ ñîãëàñèÿ.

Êðèòåðèé Ñòüþäåíòà ñëóæèò äëÿ ñðàâíåíèÿ ñðåäíåãî àðèôìåòè÷åñêî-

ãî ñëó÷àéíîé âåëè÷èíû t

ñð

c ìàòåìàòè÷åñêèì îæèäàíèåì ðàñïðåäåëåíèÿ:

(

)

t Mt

. (8.45)

Ïîëó÷åííîå çíà÷åíèå ñðàâíèâàåòñÿ ñ êðèòè÷åñêèì (òàáëè÷íûì) T

êð

(f,g),

âûáèðàåìûì ïî ÷èñëó ñòåïåíåé ñâîáîäû f = n-1 è çíà÷åíèþ äîâåðèòåëü-

íîé âåðîÿòíîñòè g (ïðèë.I). Åñëè T £ T

êð

(f,g), òî ãèïîòåçà î âèäå ôóíêöèè

ðàñïðåäåëåíèÿ ïðèíèìàåòñÿ. Â ñëó÷àå îòðèöàòåëüíîãî ðåçóëüòàòà íåîáõî-

äèìî ïåðåñìîòðåòü ãèïîòåçó î ôóíêöèè ðàñïðåäåëåíèÿ èëè èçìåíèòü ïàðà-

ìåòðû ïëàíà èñïûòàíèé.

Òàáëèöà 8.9

ПОСТРОЕНИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ

Íîìåð

èíòåð-

Ãðàíèöû

èíòåðâàëîâ

*(t

max

)

F(t

min

)

F(t

max

)

Ðàñ÷åòíîå

÷èñëî

âàëà,

min

max

ïîïàäàíèé,

-¥

0 0

0 0,0000

0,0077

0,39

1 20

0,002

0,04

0,04 0,0077

0,0362

0,0285

1,42

2 40

0,004

0,08

0,12 0,0362

0,1206

0,0844

4,22

3 60

0,005

0,10

0,22 0,1206

0,2922

0,1716

8,58

4 80

100

0,012

0,24

0,46 0,2922

0,5311

0,2389

11,95

5 100

120

0,017

0,34

0,80 0,5311

0,7590

0,2279

11,39

6 120

140

0,007

0,14

0,94 0,7590

0,9079

0,1489

7,45

7 140

160

0,002

0,04

0,98 0,9079

0,9746

0,0667

3,33

8 160

180

0,001

0,02

1,00 0,9746

0,9950

0,0204

1,02

180

+¥

0 0

1 0,9950

1,0000

0,0050

0,25

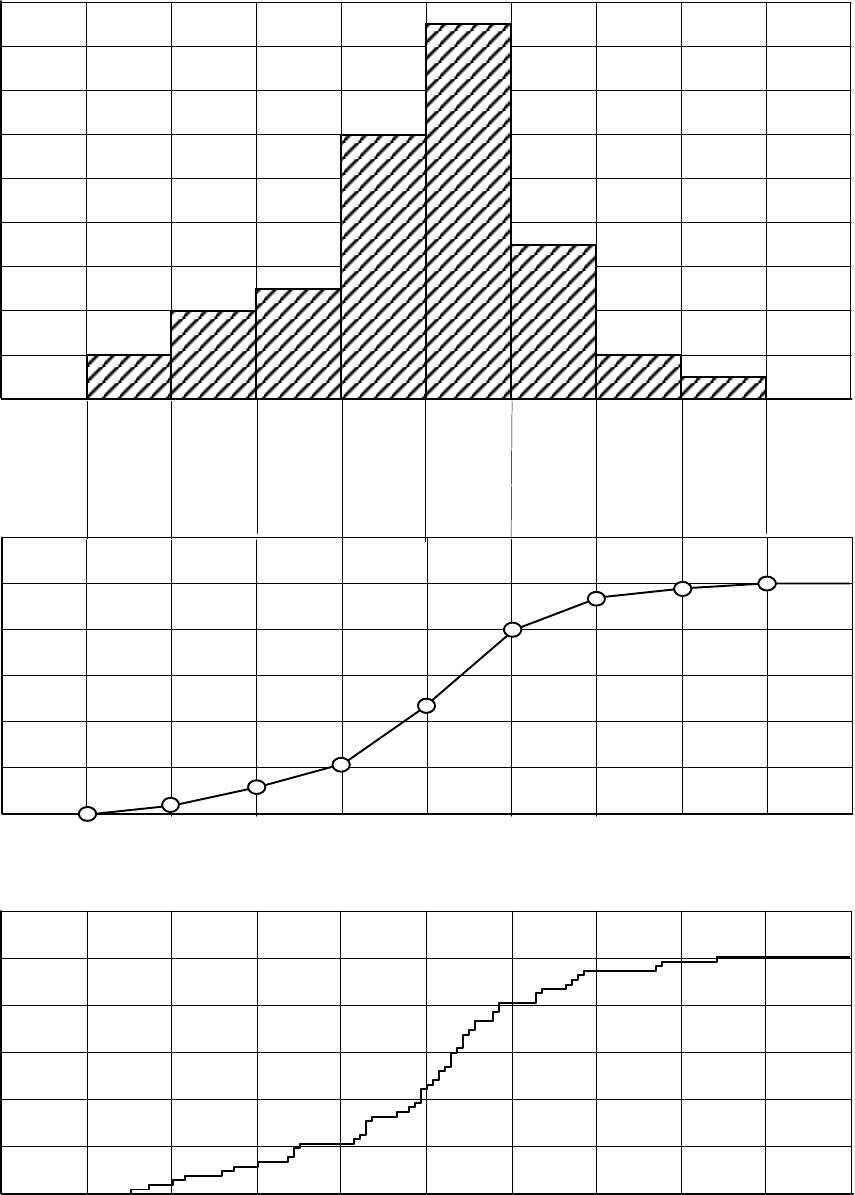
137

0,002

0,004

0,006

0,008

0,010

0,012

0,014

0,016

20 40 60 80 100 120 140 160 1800

0,2

0,4

0,6

0,8

1,0

0,2

0,4

0,6

0,8

1,0

Ðèñ.8.5. Ïîñòðîåíèå ñòàòèñòè÷åñêèõ ãðàôèêîâ (ê ïðèìåðó 8.13):

à - ãèñòîãðàììà íàðàáîòêè, á - ñòàòèñòè÷åñêàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ,

â - íåñãðóïïèðîâàííàÿ ñòàòèñòè÷åñêàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ.

138

Ïðèìåð 8.14. Äëÿ ïðèìåðà 8.13 çíà÷åíèå êðèòåðèÿ Ñòüþäåíòà ïî ôîðìóëå (8.45)

, ,

9886 975

320

00425

ãäå t

ñð

= 98,86 ÷ - ñðåäíåå àðèôìåòè÷åñêîå íàðàáîòîê.

Òàáëè÷íîå çíà÷åíèå êðèòåðèÿ Ñòüþäåíòà ïðè ÷èñëå ñòåïåíåé ñâîáîäû f = n-1 = 49

è ïðèíÿòîì çíà÷åíèè äîâåðèòåëüíîé âåðîÿòíîñòè g = 0,95 T

êð

(f,g) = 1,677 (ñì.ïðèë.I).

Òàê êàê T < T

êð

(f,g), òî ãèïîòåçà î âèäå ôóíêöèè ðàñïðåäåëåíèÿ ïðèíèìàåòñÿ.

Êðèòåðèé Ïèðñîíà (êðèòåðèé ñîîòâåòñòâèÿ) c

îïðåäåëÿåò îòêëîíåíèå

èñòèííîãî ðàñïðåäåëåíèÿ îò ãèïîòåòè÷åñêîãî è ïîçâîëÿåò ïðîâåðèòü ñîîò-

âåòñòâèå ýêñïåðèìåíòàëüíûõ äàííûõ ïðåäïîëàãàåìîé ôóíêöèè. Ðàñ÷åòíîå

çíà÷åíèå êðèòåðèÿ - ñóììà îòíîñèòåëüíûõ ðàñõîæäåíèé ôàêòè÷åñêîãî è

ðàñ÷åòíîãî ÷èñåë íàáëþäåíèÿ ñëó÷àéíîé íàðàáîòêè â êàæäîì èíòåðâàëå

(

)

(

)

2 2

= -

åå

D Dn np

j j

(8.46)

ñðàâíèâàåòñÿ ñ òàáëè÷íûì êðèòè÷åñêèì çíà÷åíèåì c

êð

(f,g) (ïðèë.I) äëÿ

÷èñëà ñòåïåíåé ñâîáîäû f = n-c-1 è äîâåðèòåëüíîé âåðîÿòíîñòè g èëè

óðîâíÿ çíà÷èìîñòè a = 1-g (ãäå c - êîëè÷åñòâî èñïîëüçóåìûõ âûáîðî÷íûõ

îöåíîê ïàðàìåòðîâ ïðîâåðÿåìîãî òåîðåòè÷åñêîãî ðàñïðåäåëåíèÿ). Ãèïîòåçà

î ôóíêöèè ðàñïðåäåëåíèÿ ïðèíèìàåòñÿ, åñëè c

< c

êð

(f,g). Âåëè÷èíà äî-

âåðèòåëüíîé âåðîÿòíîñòè îáû÷íî ïðèíèìàåòñÿ íå ìåíåå 0,9.

Äëÿ èñïîëüçîâàíèÿ êðèòåðèÿ ñîãëàñèÿ Ïèðñîíà íåîáõîäèìî çíàòü âñå

ïàðàìåòðû ïðîâåðÿåìîãî ðàñïðåäåëåíèÿ, ÷òîáû ìîæíî áûëî âû÷èñëèòü

çíà÷åíèÿ åãî òåîðåòè÷åñêîé èíòåãðàëüíîé ôóíêöèè F(t) â ëþáîé òî÷êå t.

Ïðè îöåíêå ñîãëàñèÿ âìåñòî òåîðåòè÷åñêèõ çíà÷åíèé ïàðàìåòðîâ ðàñïðå-

äåëåíèé èñïîëüçóþòñÿ èõ âûáîðî÷íûå òî÷å÷íûå îöåíêè (t* è s*).

Åñëè âûáîðî÷íàÿ ñîâîêóïíîñòü áûëà ñôîðìèðîâàíà ïðè èñïûòàíèÿõ ïî

ïëàíó [NUN], îöåíêîé ìàòåìàòè÷åñêîãî îæèäàíèÿ ÿâëÿåòñÿ ñðåäíåå àðèô-

ìåòè÷åñêîå, ïðè äðóãèõ ïëàíàõ èñïûòàíèé â êà÷åñòâå îöåíêè ìîæíî èñ-

ïîëüçîâàòü òî÷å÷íûå îöåíêè ñðåäíåé íàðàáîòêè (8.35)-(8.38), îäíàêî äîñ-

òîâåðíîñòü âûÿâëåííîãî ðàñïðåäåëåíèÿ ïðè ýòîì áóäåò äîâîëüíî íèçêîé.

Îöåíêà ñðåäíåãî êâàäðàòè÷åñêîãî îòêëîíåíèÿ

( )

s* * *=

- =

= =

å å

1 1

t t

n n

t t

. (8.47)

Â ñëó÷àå ëîãàðèôìè÷åñêè-íîðìàëüíîãî ðàñïðåäåëåíèÿ â êà÷åñòâå ïàðà-

ìåòðîâ ðàñïðåäåëåíèÿ èñïîëüçóþòñÿ ñðåäíåå àðèôìåòè÷åñêîå è ñðåäíåå

êâàäðàòè÷åñêîå îòêëîíåíèå ëîãàðèôìà íàðàáîòêè.

Ïðè ïðîâåðêå ñîãëàñèÿ ïî êðèòåðèþ Ïèðñîíà îáû÷íî èñïîëüçóþòñÿ èí-

òåðâàëû, âûäåëåííûå äëÿ ãðóïïèðîâàíèÿ âàðèàöèîííîãî ðÿäà. Âåëè÷èíà

òåîðåòè÷åñêîé âåðîÿòíîñòè ïîïàäàíèÿ ñëó÷àéíîé íàðàáîòêè â j-é èíòåðâàë:

= P(t

min

£t£t

max

) = F(t

max

) - F(t

min

). (8.48)

Ïîñêîëüêó òåîðåòè÷åñêàÿ ñëó÷àéíàÿ íàðàáîòêà t ìîæåò ïðèíèìàòü çíà-

÷åíèÿ îò 0 äî ¥, à èíòåðâàëû ãðóïïèðîâàíèÿ îõâàòûâàþò òîëüêî ðàçìàõ

âàðèàöèîííîãî ðÿäà R

(8.39), íåîáõîäèìî ïî ôîðìóëå (8.48) òàêæå âû÷èñ-

139

ëèòü òåîðåòè÷åñêóþ âåðîÿòíîñòü äëÿ "íóëåâîãî" èíòåðâàëà (j=0) ñ ãðàíè-

öàìè îò t

min

=0 äî t

max

min

è (k+1)-ãî èíòåðâàëà ñ ãðàíèöàìè îò

k+1

min

max

äî t

k+1

max

=¥. Ïîíÿòíî, ÷òî äëÿ j=0 è j=k+1 âñåãäà Dn

=0.

Ïðèìåð 8.15. Äëÿ îïðåäåëåíèÿ êðèòåðèÿ Ïèðñîíà ïî äàííûì ïðèìåðà 8.13 ìîæíî

èñïîëüçîâàòü òå æå èíòåðâàëû, ÷òî è ïðè ïîñòðîåíèè ãèñòîãðàììû. Ðàñ÷åòíûå çíà÷åíèÿ

âåðîÿòíîñòè ïîïàäàíèÿ íàðàáîòêè â êàæäûé èíòåðâàë p

è îæèäàåìîãî ÷èñëà ïîïàäàíèé

ïðèâåäåíû â òàáë.8.9. Çíà÷åíèÿ F(t

max

) è F(t

min

) ðàññ÷èòàíû ïî ïðèíÿòûì çíà÷å-

íèÿì m = 97,5 è s = 32,0. Êðèòåðèé Ïèðñîíà

= (2

/1,42) + (4

/4,22) + (5

/8,58) + (12

/11,95) +

+ (17

/11,39) + (7

/7,45) + (2

/3,33) + (1

/1,02) - 50 = 5,69.

Òàáëè÷íîå çíà÷åíèå êðèòåðèÿ ïðè ÷èñëå ñòåïåíåé ñâîáîäû f = n-c-1 = 50-2-1 = 47

è äîâåðèòåëüíîé âåðîÿòíîñòè g = 0,95 c

êð

(f,g) = 32,3 (ñì.ïðèë.I) . Òàê êàê c

êð

(f,g), òî ãèïîòåçà î ôóíêöèè ðàñïðåäåëåíèÿ ïðèíèìàåòñÿ.

Êðèòåðèé Êîëìîãîðîâà ïîçâîëÿåò îöåíèòü äîïóñòèìîñòü ìàêñèìàëüíî-

ãî îòêëîíåíèÿ ãèïîòåòè÷åñêîé (ðàñ÷åòíîé) ôóíêöèè ðàñïðåäåëåíèÿ F(t) îò

çíà÷åíèé, ïîëó÷åííûõ ïî ýêñïåðèìåíòàëüíûì äàííûì. Äëÿ ïðîâåðêè ìàê-

ñèìàëüíîå îòêëîíåíèå

D = max|F(t)

F*(t)|. (8.49)

ñðàâíèâàåòñÿ ñ êðèòè÷åñêèì çíà÷åíèåì D

êð

(n,a), êîòîðîå âûáèðàåòñÿ ïî

òàáëèöàì èñõîäÿ èç ÷èñëà ýêñïåðèìåíòîâ n è óðîâíÿ çíà÷èìîñòè a

(ñì.ïðèë.I). Ãèïîòåçà ïðèíèìàåòñÿ, åñëè D < D

êð

(n,a). Â êà÷åñòâå ñòàòè-

ñòè÷åñêîé èíòåãðàëüíîé ôóíêöèè ðàñïðåäåëåíèÿ F*(t) ïðåäïî÷òèòåëüíî

èñïîëüçîâàòü íåñãðóïïèðîâàííóþ ôóíêöèþ ðàñïðåäåëåíèÿ êàê íàèáîëåå

ïîäðîáíî îòîáðàæàþùóþ âûáîðî÷íóþ ñîâîêóïíîñòü {t

Êðèòåðèé Êîëìîãîðîâà óäîáíåå èñïîëüçîâàòü â ñëó÷àå, êîãäà âûáîð âè-

äà ðàñïðåäåëåíèÿ ïðîèçâîäèòñÿ ïî êîîðäèíàòíûì ñåòêàì. Ïðè ýòîì íå

îáÿçàòåëüíî çàðàíåå âû÷èñëÿòü ïàðàìåòðû ïðîâåðÿåìîãî ðàñïðåäåëåíèÿ è

ñòðîèòü åãî ãðàôèê, - äîñòàòî÷íî ïðîâåñòè ïðÿìóþ ëèíèþ, íàèëó÷øèì îá-

ðàçîì ïðîõîäÿùóþ ÷åðåç ìíîæåñòâî òî÷åê (t

*) è â êà÷åñòâå ìàêñè-

ìàëüíîãî ðàñõîæäåíèÿ (8.49) âçÿòü ìàêñèìàëüíîå (ñ ó÷åòîì íåëèíåéíîñòè

ìàñøòàáà) îòêëîíåíèå ýêñïåðèìåíòàëüíûõ òî÷åê îò ýòîé ëèíèè. Ïðèìåíå-

íèå êðèòåðèÿ Ïèðñîíà óäîáíåå, åñëè íà ýòàïå âûáîðà çàêîíà ðàñïðåäåëå-

íèÿ F(t) ïðîèçâîäèëîñü ãðóïïèðîâàíèå ýêñïåðèìåíòàëüíûõ äàííûõ è

ñòðîèëàñü ãèñòîãðàììà.

Ïðèìåð 8.16. Äîïóñòèìîñòü ìàêñèìàëüíîãî îòêëîíåíèÿ ðàñ÷åòíîé ôóíêöèè ðàñ-

ïðåäåëåíèÿ F(t) îò çíà÷åíèé, ïîëó÷åííûõ ïî ýêñïåðèìåíòàëüíûì äàííûì F*(t) ïðèìå-

ðà 8.13 îïðåäåëÿåì ïî êðèòåðèþ Êîëìîãîðîâà (8.49). Çíà÷åíèÿ îòêëîíåíèÿ

|F(t)

F*(t)| äëÿ âñåõ 50 òî÷åê ïðèâåäåíû â òàáë.8.8. Èç òàáëèöû ñëåäóåò D =

max|F(t)

F*(t)| = 0,1018. Òàê êàê D < D

êð

(n,a) = D

êð

(50,a) = 0,188 (ñì.ïðèë.I), òî

ãèïîòåçà î ôóíêöèè ðàñïðåäåëåíèÿ ïðèíèìàåòñÿ.

Èç ðàññìîòðåííûõ êðèòåðèåâ íàèáîëüøåé äîñòîâåðíîñòüþ îáëàäàåò

êðèòåðèé Ïèðñîíà, ïîñêîëüêó îí ó÷èòûâàåò ðàñõîæäåíèå òåîðåòè÷åñêîé è

ñòàòèñòè÷åñêîé èíòåãðàëüíûõ ôóíêöèé ðàñïðåäåëåíèÿ âî âñåì äèàïàçîíå

èçìåíåíèÿ ñëó÷àéíîé íàðàáîòêè.

8.2.6. Интервальное оценивание показателей надежности

Èñõîäíûìè äàííûìè äëÿ èíòåðâàëüíîãî îöåíèâàíèÿ ñëóæàò âûáîðî÷íàÿ

òî÷å÷íàÿ îöåíêà ñðåäíåé íàðàáîòêè t* è âèä ðàñïðåäåëåíèÿ ñëó÷àéíîé íà-

ðàáîòêè (èëè ðåñóðñà).

140

Òî÷å÷íàÿ âûáîðî÷íàÿ îöåíêà t* ÿâëÿåòñÿ ñëó÷àéíîé âåëè÷èíîé è ìåíÿ-

åòñÿ îò âûáîðêè ê âûáîðêå, òàê ÷òî ãåíåðàëüíàÿ ñðåäíÿÿ íàðàáîòêà åñòü

ìàòåìàòè÷åñêîå îæèäàíèå âûáîðî÷íîé îöåíêè. Åñëè áû áûëî èçâåñòíî ðàñ-

ïðåäåëåíèå âåëè÷èíû t* (ôóíêöèè`f(t*) èëè

F(t*)), ìîæíî áûëî áû çàïè-

ñàòü

( )

()

g= £ £ = = -

Pt t t ftdt Ft Ft

* * . (8.50)

Âûÿâëåíèå âèäà ðàñïðåäåëåíèÿ`f(t*) ïî ýêñïåðèìåíòàëüíûì äàííûì

ïîòðåáîâàëî áû ñîâîêóïíîñòè âûáîðî÷íûõ ñðåäíèõ {t

*}, äëÿ ÷åãî íóæíî

èñïûòàòü ñîîòâåòñòâóþùåå êîëè÷åñòâî íåçàâèñèìûõ âûáîðîê. Ïîýòîìó âèä

ðàñïðåäåëåíèÿ`f(t*) è åãî ïàðàìåòðû óñòàíàâëèâàþòñÿ êîñâåííûì ïóòåì.

Ïðè íîðìàëüíîì è óñå÷åííîì íîðìàëüíîì ðàñïðåäåëåíèè íàðàáîòêè t

âûáîðî÷íîå ñðåäíåå t* òàêæå ðàñïðåäåëåíî íîðìàëüíî ïðè ëþáîì îáúåìå

âûáîðî÷íîé ñîâîêóïíîñòè n, ïðè÷åì ñðåäíåå êâàäðàòè÷åñêîå îòêëîíåíèå

âûáîðî÷íûõ ñðåäíèõ s

ðàç ìåíüøå ñðåäíåãî êâàäðàòè÷åñêîãî îòêëî-

íåíèÿ ñëó÷àéíîé âåëè÷èíû â âûáîðêå

s s

n= . (8.51)

Äëÿ îäíîñòîðîííåãî äîâåðèòåëüíîãî èíòåðâàëà, îãðàíè÷åííîãî ñâåðõó

( ) ( )

g a e e

= - = £ + = - £ =

1 Pt t Pt t P

t t

* *

. (8.52)

Ïîñëåäíåå ðàâåíñòâî â âûðàæåíèè (8.52) ïî ñóòè åñòü îïðåäåëåíèå èí-

òåãðàëüíîé ôóíêöèè ðàñïðåäåëåíèÿ ñëó÷àéíîé âåëè÷èíû (t

t*)/s

âèäà

F(t)=P(t£t

). Ñëåäîâàòåëüíî, g = 1-`a - çíà÷åíèå ôóíêöèè ðàñïðåäåëåíèÿ

è âåëè÷èíó e/s

â âûðàæåíèè (8.52) ìîæíî çàìåíèòü íà òàêîå çíà÷åíèå

àðãóìåíòà ôóíêöèè ðàñïðåäåëåíèÿ, ïðè êîòîðîì îíà ðàâíà g. Çíà÷åíèå àð-

ãóìåíòà z

, ïðè êîòîðîì ôóíêöèÿ ðàñïðåäåëåíèÿ ïðèíèìàåò çíà÷åíèå g, íà-

çûâàåòñÿ êâàíòèëüþ ðàñïðåäåëåíèÿ âåðîÿòíîñòè g.

Äëÿ íîðìàëüíîãî çàêîíà êâàíòèëüþ âåðîÿòíîñòè g ÿâëÿåòñÿ íîðìèðî-

âàííîå è öåíòðèðîâàííîå çíà÷åíèå àðãóìåíòà u

( )

[

]

P Fz P

t Mt

zº =

0 g g

. (8.53)

Ïðè ýòîì F

(

z) = 1-F

(z), ò.å. z

-g

=-z

Êâàíòèëè íîðìàëüíîãî ðàñïðåäåëåíèÿ ïðèâåäåíû â ïðèë.I.

Òàê êàê âåëè÷èíà t* ðàñïðåäåëåíà íîðìàëüíî, òî âìåñòî âåëè÷èíû e/s

â âûðàæåíèè (8.52) ìîæíî çàïèñàòü êâàíòèëü íîðìàëüíîãî ðàñïðåäåëåíèÿ

âåðîÿòíîñòè 1-`a. Òîãäà ñ ýòîé âåðîÿòíîñòüþ áóäåò âûïîëíÿòüñÿ íåðàâåí-

ñòâî

z z tt z

t z

£ = £ + = -

- -

* *

a a a1 1

èëè . (8.54)

Ïðàâàÿ ÷àñòü âòîðîãî íåðàâåíñòâà (8.54) - âåðõíÿÿ äîâåðèòåëüíàÿ ãðà-

íèöà îäíîñòîðîííåãî èíòåðâàëà ñ óðîâíåì çíà÷èìîñòè`a: