Найханова Л.В., Дамбаева С.В. Методы и алгоритмы принятия решений в управлении учебным процессом в условиях неопределенности
Подождите немного. Документ загружается.


91
3.3.2 Методы оптимизации графа межпредметных связей
Характерной особенностью графа междисциплинарных связей является наличие
большого количества дуг, связывающих вершины графа. Впоследствии это может вызвать
затруднения в распределении дисциплин по семестрам. Для уменьшения размерности графа
межпредметных связей используются следующие методы: выявления и устранения
контуров; исключения несущественных или эквивалентных путей; исключения связей,
перекрещивающих слои графа.
3.3.2.1 Выявление и удаление контуров
Введем несколько определений [59]:
Определение 3.4. Маршрут (путь) – это такая последовательность конечного или
бесконечного числа ребер (l
1
, l
2
, l
3
,…,l
n
), что каждые два соседних ребра l
i-1
и l
i
инцидентны
одной вершине (смежные).
Определение 3.5. Вершина V
0
, инцидентная ребру l
1
, называется началом маршрута, а
вершина V
n
, инцидентная ребру l
n
называется концом маршрута.
Определение 3.6. Если V
0
= V
n
, где V
0
– начало маршрута, а V
n
– конец маршрута, то
маршрут называют циклическим или контуром.
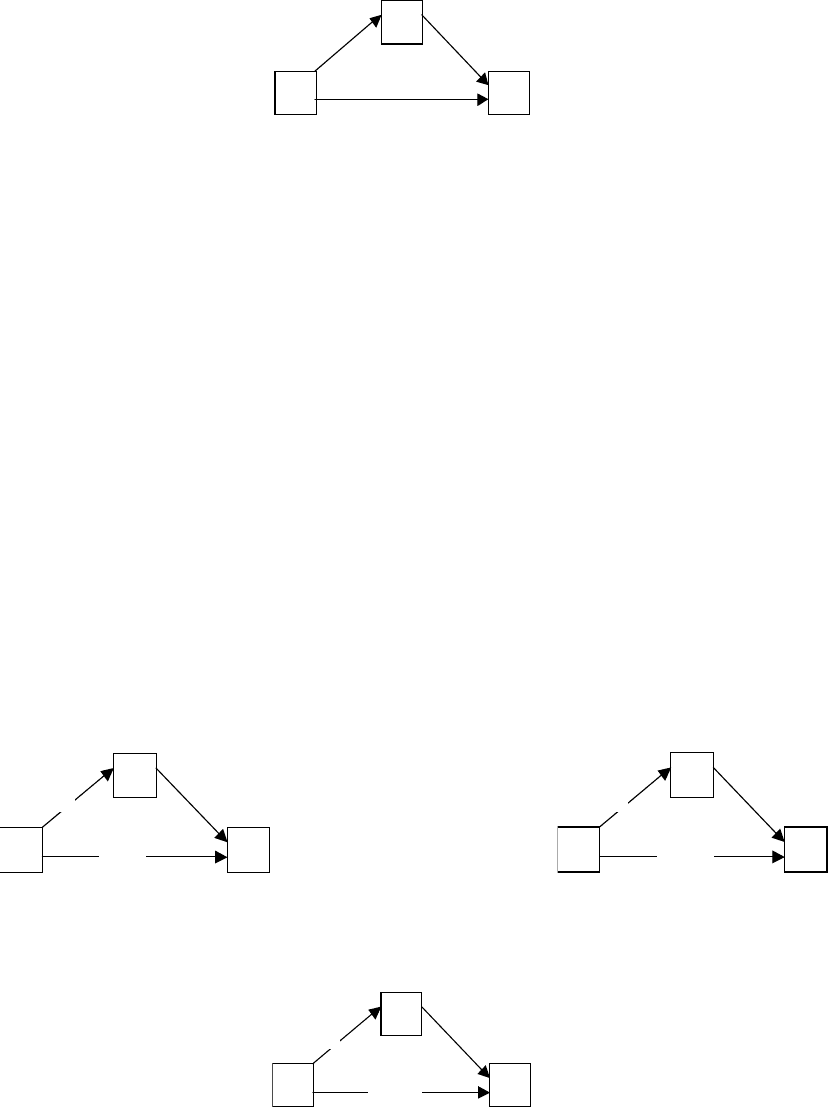
Возможны два случая образования контуров:
1. Наличие перекрестных связей между дисциплинами. Например, в результате
нарушения логики взаимосвязей между дисциплинами для начала изучения одного курса
требуется знание другого, и наоборот (рисунок 3.18а).
2. Необходимость параллельного изучения курсов с попеременной передачей
информации из одного курса в другой (рисунок 3.18б).
В процессе анализа графа межпредметных связей G(D,U) необходимо выявить
контуры, которые должны быть предоставлены ЛПР для их разрыва. В первом случае ЛПР
должен пересмотреть содержание курсов и ликвидировать противоречивые требования
путем перераспределения учебного материала или объединения дисциплин, входящих в
цикл. При возникновении второй ситуации необходимо провести детальный анализ и
выявить возможность параллельного изучения дисциплин или же обосновать необходимость
разрыва в изучении того или иного курса.
Алгоритм выявления контуров основан на методе поиска в глубину:
1.
Формируется множество вершин контура R = {r}, где r – вершина, входящая в
контур.
2.
Добавить во множество R вершину {k | (i,k) ≠ 0 и k ∉ R}.
3.
Если вершина k∈R, то обнаружен цикл и далее п.4, иначе п. 5.
4.
Двигаясь в обратном порядке, обнаружить вершины, входящие в цикл, и обнулить
связь [j,k], где j – последняя вершина, смежная k.
5.
Если есть смежные вершины вершине K, то повторить п. 2, иначе обнулить
элемент матрицы [j,k], где j – последняя вершина, смежная k.
6.
Повторять для всех вершин с п.1.
1
2
3
а) Перекрестные ссылки
1
2
б) Параллельные связи
Рисунок 3.18 - Возможные случаи образования контуров
92
3.3.2.2 Метод определения несущественных связей
В работах [57,59] дано следующее определение эквивалентных связей.
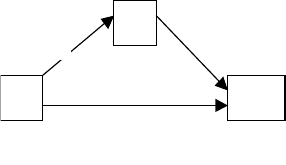
Определение 3.7. Эквивалентными называются связи между двумя вершинами,
имеющие различные пути. Так, например, связи 1 → 3 и 1 → 2 → 3 являются
эквивалентными. Они представлены на рисунке 3.19.
1
2
3
Рисунок 3.19 - Эквивалентные связи
Связи, представленные однозвенным путем, называются несущественными или
непосредственными. В приведенном выше примере связь 1 → 3 – несущественная. Связи,
содержащие многозвенные пути, называются транзитными (1 → 2 → 3). Связи, являющиеся
несущественными согласно данному определению, удаляются.
Однако в данном определении не учитываются:
а)
теснота связи между дисциплинами, которая может быть представлена весом
дуги, связывающей две вершины. Удаление несущественной связи без учета
тесноты может привести к удалению связи, имеющей очень большой вес, и
тогда возникает большой разрыв между дисциплиной-предком и
дисциплиной-потомком, использующей много понятий из дисциплины-предка.
б)
состав базовых понятий в дисциплинах-потомках, передаваемых из одной
дисциплины-предка.
Если рассматривать граф, который представлен на рисунке 3.8 без учета весовых
коэффициентов, то связь между дисциплинами 1→3 является несущественной и ее можно
удалить, так как для изучения дисциплины 3 необходимо изучить дисциплину 2, т.е.
дисциплина - потомок (3) не может изучаться раньше дисциплины - предка (2).
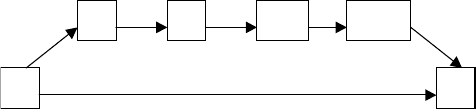
Рассмотрим случай, когда на графе указаны веса дуг. Разрыв несущественной связи
во многом зависит от весовых коэффициентов. На рисунках 3.20 а, б, в представлены
возможные варианты распределения на подграфе, состоящем из трех вершин.
1
2
3
20
4
3
1
2
3
3
10
4
а) вес дуги (1,2) больше веса дуги (1,3) б) вес дуги (1,3) больше веса дуги (1,2)
1
2
3
6
6
4
в) веса дуг (1,2) и (1,3) равны.
Рисунок 3.20 - Возможные случаи распределения значения весовых коэффициентов на графе
Пусть имеется взвешенный граф междисциплинарных связей G(D,U), где
D = {d
1
,d
2
,…,d
n
}– множество вершин графа;
93
U = {u}- множество ребер графа;
a
ij
– вес дуги u
ij.
Рассмотрим подграф G'(D',U') графа G, где:
D'⊆D, D'={d
i
, d
j
, d
k
}, где i, j, k – номера вершин подграфа;
U'⊆U, U'={u
ij
,u
ik
,u
jk
} – дуги подграфа, характеризуемые весами соответственно a
ij
,
a
ik
, a
jk
. Граф G'(D',U') представлен на рисунке 3.21.
d
i
d
j
d
k
a
ij
a
ik
a
jk
Рисунок 3.21 - Подграф из трех вершин
P
i
– множество модулей i-той дисциплины;
B
j
– базовые модули j-той дисциплины;
B
k
– базовые модули k-той дисциплины.
Пусть П – это множество модулей, которые входят в B
j
и B
k
, и наследуются от i-той
дисциплины.
П = P
i
∩B
j
∩B
k
.
(3.11)
Возможен один из вариантов значения множества П:
1)
П = ∅ - нельзя удалить дугу (d
i
,d
k
) – является существенной;
2)
П ≠ ∅. В этом случае необходимо скорректировать значение веса дуги (d
i
,d
k
)
следующим образом:
a'
ik
= a
ik
– |П| (3.12)
Из формул (3.11) и (3.12) следует, что величина a'
ik
может принимать только
неотрицательные значения. Если a'
ik
> 0, то дуга (d
i
,d
k
) менее существенная и удалять ее
нежелательно. Если a'
ik
= 0, то в данном случае дуга (d
i
,d
k
) – несущественная и ее можно
удалить.
Таким образом, с учетом тесноты и содержания междисциплинарных связей
необходимо переопределить понятие существенности связей:
Определение 3.8. Связь (i,k) называется несущественной в том случае, если (B
k
∩P
i
) ⊂
(B
j
∩P
i
), т.е. все модули, которые связывают дисциплины i и k, включены во множество
модулей, которые связывают дисциплины i и j.
Определение 3.9. Менее существенной называется связь (i, k), когда множество
модулей, которые связывают дисциплины i и k, частично включены во множество модулей,
которые связывают дисциплины i и j.
Определение 3.10. Существенной называется такая связь (i,k), у которой
(B
k
∩P
i
)
∩
(B
j
∩P
i
) = ∅, т.е. множество модулей, связывающих дисциплины i и k, не включено
во множество модулей, связывающих дисциплины i и k.
Несущественные связи в эквивалентных путях необходимо удалять. Менее
существенные связи нежелательно удалять. Существенные связи нельзя удалять.
Алгоритм обнаружения эквивалентных связей:
1.
Список А пуст;
2.
Найти пару (i,j)≠0 и сформировать список А ={k | (i,k) ≠0 и k
≠
j};
3.
Проверить наличие вершины j в списке А. Если она есть, то обнаружены
эквивалентные связи, иначе п. 4.
4.
Если список пуст, то повторить с п. 1 для следующей пары (i,j);
5.
Извлечь из списка первый элемент k. Добавить в конец списка элементы {l | (k,l) ≠0
и l∉А}. Далее п.3.
94
6.
Произвести корректировку веса дуги (i,j) по формуле (3.12).
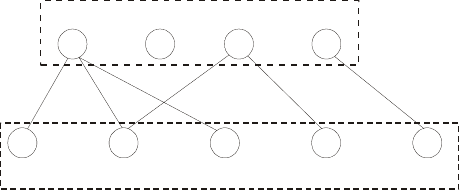
Если в транзитных путях эквивалентных связей имеется не одна, а множество
вершин, то этот случай можно привести к рассмотренному ранее случаю из трех вершин
(рисунок 3.22).
1
2 3 … n-1
n
Рисунок 3.22 - Многозвенный транзитный путь
В этом случае вершины 2 … n-1 можно объединить в одну вершину, и привести
данный случай к случаю из трех вершин.
3.3.3 Алгоритм формирования уровней базовой таксономии
Базовая таксономия характеризует «провязку» всех дисциплин отношением
«наследование знаний». От правильности построения базовой таксономии зависит качество
построения оптимального учебного плана, т.к. основным требованием к его построению
является последовательность, логичность обучения. Это требование предполагает, что
изучение базовой дисциплины должно предшествовать изучению опирающейся на неё
дисциплины. Отсутствие последовательности в обучении приводит к снижению его качества
и непроизвольным затратам учебного времени. Построение базовой таксономии позволяет
формировать варианты учебного плана с учетом этих требований.
Алгоритм формирования уровней базовой таксономии:
1. Определить дисциплины, у которых нет базовых дисциплин. Эти дисциплины
составляют первый уровень базовой таксономии.
2. В следующий уровень включаются те дисциплины, у которых все базовые
дисциплины распределены на предыдущих уровнях.
Базовые таксономии, полученные в результате проведения вычислительных
экспериментов, приведены в Приложении Г.
3.4 Методы и алгоритмы распределения дисциплин по семестрам
Имея полный список дисциплин специальности, зная продолжительность их
изучения и базовую таксономию, в которой все дисциплины упорядочены по отношению
«наследование знаний», можно решать задачу распределения дисциплин по семестрам.
Анализ предметной области задачи показал, что множество ограничений,
накладываемых на учебный план, можно разбить на группы по характеру применения.
1. Ограничения на учебный план семестра:
- количество дисциплин в семестре;
- средняя аудиторная нагрузка;
- интенсивность изучения дисциплин.
2. Ограничения на учебный план в целом:
- соответствие суммарного объема часов установленной норме;
- соответствие отношения федерального и национально-регионального
компонентов.
3. Ограничения на перераспределение часов:
- допустимое изменение часов в пределах ±5% внутри цикла;
- допустимое изменение часов в пределах ±10% между циклами.
В работе предлагается производить распределение дисциплин по семестрам,
упорядоченных по требованию последовательности и логичности обучения и образующих
95
базовую таксономию дисциплин.
Анализ ограничений показал, что многие из них не являются строго определенными.
Например, ограничение, налагающееся на изменение часов, гласит, что допустимый предел
изменения должен быть не больше 5%. Поэтому подобные ограничения удобно представлять
в виде нечетких чисел. На основании этого в данной работе была предпринята попытка
создания методов для распределения дисциплин по семестрам на основе теории нечетких
множеств. Решение задачи состоит из трех подзадач:
1)
формирование учебного плана семестра;
2)
проверка списка дисциплин учебного плана семестра на соответствие ограничениям
семестра;
3)
проверка всего учебного плана на соответствие ограничениям всего учебного плана.
3.4.1 Формирование учебного плана семестра
Имеем множество дисциплин D={d
1
, d
2
,…,d
n
}, каждая дисциплина описывается
следующим кортежем <N, Cl, Cm, H, L, P>, где N – наименование дисциплины, Cl – цикл
(ГСЭ, ОПД, ЕН, СД), Cm – компонент (федеральный, национально-региональный), H –
количество часов для изучения, L – коэффициент силы междисциплинарной связи, P –
признак переноса. Необходимо проверить данное множество на соответствие ограничению
по количеству дисциплин в семестре.
Изначально предполагается, что первый уровень базовой таксономии соответствует
первому семестру. У каждой дисциплины d
i
имеется сила связи с другими дисциплинами и
признак возможности переноса на другой уровень.
Рисунок 3.23 - Связи между дисциплинами
Дисциплины ранжируются по одному из вышеописанных признаков. Исходя из
этого, можно использовать два варианта решения данной подзадачи:
- ранжирование в порядке убывания по силе связи;
- ранжирование в порядке убывания по признаку возможности переноса.
При формировании списка дисциплин для i-го семестра выполняется контроль на
соответствие ограничению по количеству дисциплин в семестре. Если сформированный
список дисциплин-претендентов не соответствует этому ограничению, производится
удаление дисциплин из списка и перенос их на нижний уровень базовой таксономии в случае
их избытка на уровне i-го семестра, в случае недостаточного количества - добавление из (i-
1)-го семестра нижнего уровня базовой таксономии.
3.4.1.1 Регулятор усреднения интенсивностей
Имеем множество дисциплин D
i
={d
1
, d
2
,…,d
n
}, интенсивности для дисциплин
каждого цикла intEN, intDS, intOPD и среднюю аудиторную нагрузку L. Необходимо
проверить, соответствуют ли значения интенсивностей и средней аудиторной нагрузки
установленным ограничениям. Для этого построим нечеткий регулятор. Нечеткий вывод в
регуляторе реализуем по алгоритму Мамдани. Рассмотрим первый регулятор.
Как было указано выше, задачей данного регулятора является приведение
интенсивностей изучения дисциплин различных циклов к одному среднему значению,
которое в дальнейшем будет использоваться регулятором, выполняющим проверку
Дисциплины го уровняi+1
Дисциплины го уровняi-
V1 1
V12 V1 3
V2 1 V2 2
V31

96
соответствия списка дисциплин семестра ограничениям, налагаемым на учебный план
семестра.
Рассмотрим формальное описание лингвистических переменных нечеткого
регулятора. Введем следующие обозначения:
EN – интенсивность дисциплин цикла ЕН;
OPD – интенсивность дисциплин цикла ОПД;
SD – интенсивность дисциплин цикла СД;
IC - интенсивность дисциплин цикла;
intAll – усредненная интенсивность дисциплин одного семестра учебного плана.
Рассмотрим формальное описание обобщенной лингвистической переменной IC.
IC = <
β
, T, U, G, M, C>:
β
- наименование переменной
β
∈{EN, OPD, SD};
T – терм-множество нечетких переменных;
U - универсальное множество лингвистической переменной IC, U=[0,50];
G - синтаксические процедуры, порождающие элементы множества T;
M - семантические процедуры, определяющие значение переменной
β
.
Формальное описание лингвистической переменной «Усредненная интенсивность»:
IntAll = <Allβ, AllT, AllX, AllG, AllM>:
All
β
- наименование переменной. All
β
= «Усредненная интенсивность»;
AllT - множество нечетких переменных;
AllX - универсальное множество лингвистической переменной intAll, U=[0,50];
AllG - синтаксические процедуры, порождающие элементы множества
IntAllT;
AllM - семантические процедуры, определяющие значение переменной
IntAll
β
.
3.4.1.2 Описание управления диапазонами универсального множества
Лингвистическая переменная IC создана для фаззификации интенсивностей
дисциплин по циклам ЕН, ОПД и СД. В терм-множество Т лингвистической переменной
включим следующие первичные термины (нечеткие переменные): НОРМА, МЕНЬШЕ
НОРМЫ и БОЛЬШЕ НОРМЫ. Формирование нечетких множеств первичных терминов
производится на основании нормальных значений интенсивностей по каждому циклу
дисциплин. Графики функций принадлежности нечетких переменных описываются
формулой 2.51.
Значение нечеткой переменной НОРМА может быть различным в зависимости от
цикла дисциплин и задается рекомендациями учебно-методического совета по
специальности и вуза по составлению учебного плана специальности, а также
предпочтениями ЛПР. На рисунке 3.24 представлено разбиение на диапазоны
универсального множества U.
Рисунок 3.24 - Разбиение на диапазоны универсального множества U
Выполнение настройки диапазонов универсального множества U лингвистической
переменной IC заключается в настройке первичных терминов терм-множества Т на
нормальные значения интенсивностей изучения дисциплин циклов.
Рассмотрим настройку нечеткой переменной НОРМА, которая заключается в
задании константы с функции принадлежности этой нечеткой переменной. Константа с
н
равна среднему значению интенсивности изучения дисциплин i-того цикла (ЕН или ОПД,
или СД), a
н
и b
н
вычисляются как процент отклонения от нормы: с
н
– задаваемое среднее
значение интенсивности изучения дисциплин i-того цикла; a
н
– нижняя граница отклонения
0 Low
α
Normal
β
High
97
от нормы, a
н
= с
н
- с
н
*
δ
, где
δ
– процент отклонения от нормы; b
н
– верхняя граница
отклонения от нормы, b
н
= с
н
+ с
н
*
δ
.
Определим константы с, a и b для нечетких переменных МЕНЬШЕ НОРМЫ и
БОЛЬШЕ НОРМЫ: с
мн
– нижняя граница универсального множества U, =inf(u), a
мн
= с
н
,
b
мн
= a
н
; с
бн
– нижняя граница универсального множества U, с
бн
= sup(u), a
бн
= b
н
,
b
бн
= с
бн
.
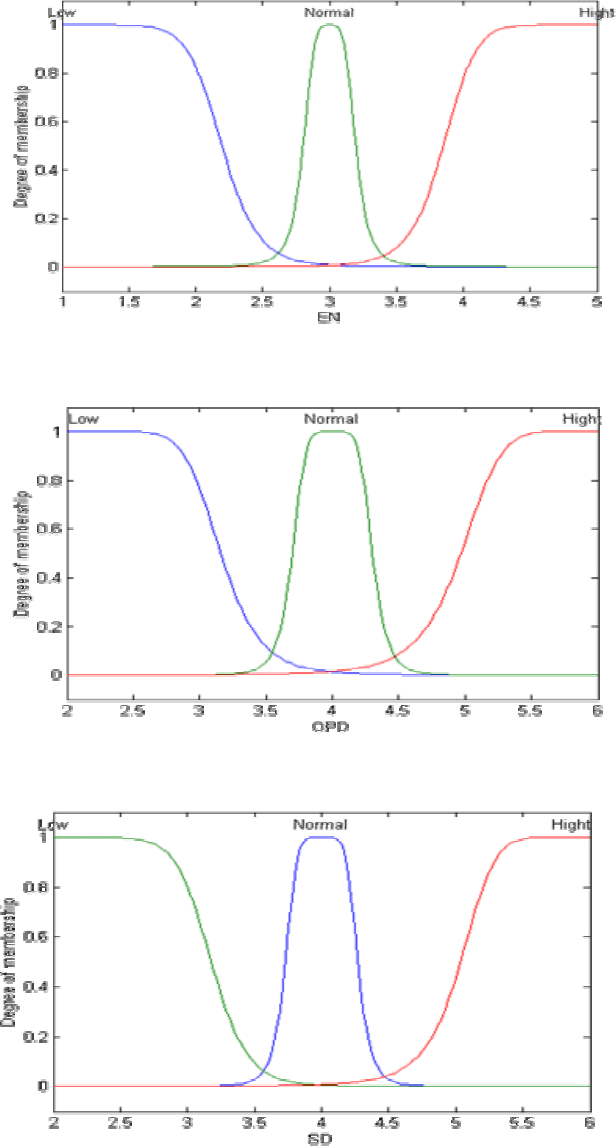
На рисунке 3.25 представлены графики функций принадлежности и разбиение
универсального множества U лингвистической переменной IC для различных циклов
дисциплин: при
β
= «ЕН» и с
н
=3;
β
= «ОПД» и с
н
=4;
β
= «СД» и с
н
=4.
в
)
интенсивность
д
ис
ц
иплин
ц
икла С
Д
а
)
интенсивность
д
ис
ц
иплин
ц
икла ЕН
б
)
интенсивность
д
ис
ц
иплин
ц
икла ОП
Д
98
Рисунок 3.25 - Функции принадлежности лингвистических переменных
На основании разбиений универсальных множеств, приведенных выше, мы имеем
следующие множества для нечетких переменных:
T = {Low, Normal, High};
Т
IntAll
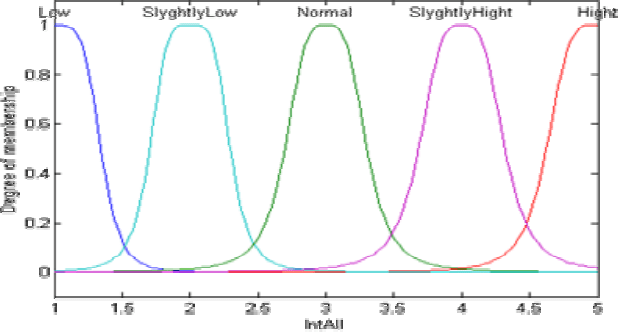
= {Low, SlightlyLow, Normal, SlightlyHigh, High}.
Терм-множества Т
IntAll
лингвистической переменной IntAll сформированно на основе
использования метода генерации составных терминов из первичных.
3.4.2.2 База правил нечеткого регулятора и алгоритм нечеткого вывода
Сформируем продукционные правила, отражающие предпочтения ЛПР в виде
нечетких логических правил усреднения интенсивностей, которые составят базу правил
нечеткого регулятора. Эти правила имеют следующий вид:
1.
If (EN=Low) and (OPD=Low) and (SD=Low) then IntAll=Low.
2.
If (EN=Low) and (OPD=Low) and (SD=Normal) then IntAll=SlightlyLow.
3.
If (EN=Low) and (OPD=Low) and (SD=High) then IntAll=SlightlyLow.
4.
If (EN=Low) and (OPD=Normal) and (SD=Low) then IntAll=Low.
5.
If (EN=Low) and (OPD=Normal) and (SD=High) then IntAll=SlightlyHigh.
6.
If (EN=Low) and (OPD=Normal) and (SD=Normal) then IntAll=SlightlyLow.
7.
If (EN=Low) and (OPD=High) and (SD=Low) then IntAll=SlightlyLow.
8.
If (EN=Low) and (OPD=High) and (SD=Normal) then IntAll=SlightlyLow.
9.
If (EN=Low) and (OPD=High) and (SD=High) then IntAll=High.
10.
If (EN=Normal) and (OPD=Low) and (SD=Low) then IntAll=Low.
11.
If (EN=Normal) and (OPD=Low) and (SD=Normal) then IntAll=SlightlyLow.
12.
If (EN=Normal) and (OPD=Low) and (SD=High) then IntAll=SlightlyHigh.
13.
If (EN=Normal) and (OPD=Normal) and (SD=Low) then IntAll=SlightlyLow.
14.
If (EN=Normal) and (OPD=Normal) and (SD=Normal) then IntAll=High.
15.
If (EN=Normal) and (OPD=Normal) and (SD=High) then
IntAll=SlightlyHigh.
16.
If (EN=Normal) and (OPD=High) and (SD=Low) then IntAll=SlightlyHigh.
17.
If (EN=Normal) and (OPD=High) and (SD=Normal) then
IntAll=SlightlyHigh.
18.
If (EN=Normal) and (OPD=High) and (SD=High) then IntAll=High.
г
)
у
с
р
е
д
ненная интенсивность

99
19.
If (EN=High) and (OPD=Low) and (SD=Low) then IntAll=Low.
20.
If (EN=High) and (OPD=Low) and (SD=Normal) then IntAll=SlightlyHigh.
21.
If (EN=High) and (OPD=Low) and (SD=High) then IntAll= SlightlyHigh.
22.
If (EN=High) and (OPD=Normal) and (SD=Normal) then
IntAll=SlightlyHigh.
23.
If (EN=High) and (OPD=Normal) and (SD=High) then IntAll=High.
24.
If (EN=High) and (OPD=Normal) and (SD=Low) then IntAll=SlightlyHigh.
25.
If (EN=High) and (OPD=High) and (SD=Low) then IntAll= SlightlyHigh.
26.
If (EN=High) and (OPD=High) and (SD=Normal) then IntAll= High.
27.
If (EN=High) and (OPD=High) and (SD=High) then IntAll= High.
Таким образом, согласно этапам логического вывода, описанным в Приложении Б,
для функционирования регулятора далее выполняются следующие этапы:
1. Фаззификация входных значений интенсивностей дисциплин, в результате
выполнения этого этапа будет сформировано множество значений функций
принадлежностей по каждому из лингвистических термов, которое мы обозначим }{
i
bB
′
=
.
2. Агрегация выполняется для каждого из правил системы нечеткого вывода. По
формуле 3.13 выполним агрегацию.
)}.(),(min{)( BTATBAT =∨
(3.13)
3. В результате получим множество
},...,,{
21
″
″
″
=
′′
n
bbbB
, где n – общее количество
правил в системе.
4. Активизация выполняется также по правилам системы нечеткого вывода. При
выполнении агрегации используется формула (3.14). В результате выполнения данного
этапа получим совокупность множеств
q
CCC ,...,,
21
, где q – общее количество
подзаключений в базе правил.
)};(,min{)(
ycy
i
µ
µ
=
′
(3.14)
5. Аккумуляция выполняется для каждой из выходных лингвистических
переменных, принадлежащих множеству
W. В нашем случае это множество представлено
одним элементом
}{int AllW = . При выполнении аккумуляции используется формула (3.15).
)}(),(max{)( xxx
BAD
µ
µ
µ
=
(3.15)
6. Дефаззификация выполняется по формуле (3.16).
,
)(
)(*
1
1
∑
∑
=
=
=
n
i
i
n
i
ii
x
xx
y
µ
µ
(3.16)
В результате работы нечеткого регулятора мы будем иметь значение усредненной
интенсивности изучения дисциплин.
3.4.2 Регулятор проверки дисциплин семестра на ограничения
Основной целью работы данного регулятора является проверка значений
усредненной интенсивности
IntAll и средней аудиторной нагрузки Ld и принятия решения на
основе значений этих переменных. Таким образом, введем лингвистические переменные
регулятора: усредненная интенсивность –
IntAll, средняя аудиторная нагрузка – Ld, действие
системы –
Actn. Представим лингвистические переменные аналогично предыдущему
регулятору в виде кортежа <
β
, Т, X, G, М>.
Лингвистическая переменная «Средняя аудиторная нагрузка».

100
Ld = <Ld
β
, LdT, LdX, LdG, LdM>:
Ld
β
- наименование переменной. Ld
β
= «Средняя аудиторная нагрузка»;
LdT - множество нечетких переменных;
LdX - универсальное множество лингвистической переменной Ld;
LdG - синтаксические процедуры, порождающие элементы множества LdT;
LdM - семантические процедуры, определяющие значение переменной Ld
β
.
Лингвистическая переменная «Действие системы».
Act = < Ld
β
, LdT, LdX, LdG, LdM>:
Act
β
- наименование переменной. Act
β
= «Действие системы»;
ActT - множество нечетких переменных;
ActX - универсальное множество лингвистической переменной Act;
ActG - синтаксические процедуры, порождающие элементы множества ActT;
ActM - семантические процедуры, определяющие значение переменной Act
β
.
Описание лингвистической переменной «Усредненная интенсивность» аналогично
описанию, представленному в разделе 3.4.1.1. Выполним разбиение на диапазоны
универсального множества
LdX для определения множества нечетких переменных LdT. Один
из вариантов разбиения представлен на рисунке 3.26.
22
Lo w
Hig ht
Sl y g h t l y
low
Norm al
Sl y g h t l y
hight
23
25
27
29
30
Рисунок 3.26 – Разбиение универсального множества LdX.
Изучение методических рекомендаций [48] и учебных планов различных вузов
показало, что не существует строго определенных правил, предписывающих придерживаться
какого-то конкретного значения аудиторной нагрузки, которая в свою очередь является
частью общей нагрузки студента. Как правило, это значение определяется вузом, однако во
многих примерах составлений учебных планов оптимальным значением объема учебной
нагрузки являются 54 часа в неделю.
Введем следующие обозначения:
h – количество часов изучения дисциплины. В
свою очередь объем учебной нагрузки состоит из аудиторных занятий и самостоятельной
работы студента (СРС), который можно определить следующим соотношением:
SRSAudV
+
=
(3.17)
где
,
j
weekCnt
hSum
Aud =
- средняя аудиторная нагрузка,
(3.18)
AudVSRS −=
- нагрузка СРС,
(3.19)
где
hSum – сумма аудиторных часов; weekCnt
j
– количество недель в j-м семестре.
Далее определим
hSum:
,
1
∑
=
=
n
i
i
hAudhSum
(3.20)
где
hAud
i
– количество аудиторных часов для i–й дисциплины; n - количество дисциплин в
семестре.
Изначально задается общее количество часов для изучения дисциплины, которое
также состоит из объема аудиторного изучения дисциплины и СРС.
,
iii
hSRShAudh
+
=
(3.21)
где
hSRS
i
- количество аудиторных часов для i – й дисциплины.
Соотношение между
hAud
i
и hSRS
i
можно задавать по формуле (3.22), где k –
коэффициент, определяющий процент часов СРС от общего бюджета часов дисциплины.
