Наноматериалы: лабораторный практикум под ред. В.А. Мошникова
Подождите немного. Документ загружается.

21
увеличение доли ячеек 1-го типа в исходном материале из ячеек 2-го типа по-
зволяет изменять электрические свойства системы от полностью изоляцион-
ных до полностью проводящих. Но этот переход не будет равномерно растя-
нут во всем диапазоне изменения концентрации проводящих ячеек. При ма-
лых концентрациях проводящих ячеек они изолированы друг от друга и от
электродов диэлектрическими ячейками. При некоторой доле
c
x , называемой
порогом протекания, возникает стягивающий кластер, т. е. появляется прово-
димость. Вблизи порога протекания
c
x тело разбивается на части, обладаю-
щие различными свойствами. Геометрия этих разбиений каждый раз приоб-
ретает новые случайные формы, но значения порога протекания для тел бес-
конечных размеров строго определены и зависят от симметрии и размерно-
сти пространства.
Если обозначить через
(
)
xP долю проводящих ячеек по отношению к
общему количеству ячеек, входящих только в стягивающий (бесконечный)
кластер, то зависимость
P
от общей доли проводящих ячеек имеет вид, при-
веденный на рис. 2.1. Там же построена приведенная проводимость
(
)
(
)
1σσ x
системы
,
содержащей
долю
проводящих
ячеек
x
(
нормированную
к
прово
-
димости
системы
,
когда
все
ячейки
проводящие
).
Бесконечный
стягивающий
кластер
(
)
xP появляется (по определению) при значении
c
xx
=
и приобрета-
ет максимальное значение при
1
=
x
.
Легко понять и пределы изме-
нения значений
(
)
(
)
1σσ x .
Прово
-
димость
(
)
xσ возникает при
c
xx
=
и не может быть больше, чем про-
водимость
(
)
xσ системы, состоящей
только из проводящих ячеек. Как
видно из рис. 2.1, для значений
c
x <
x
< 1 не все проводящие ячей-
ки, входящие в структуру беско-
нечного кластера, участвуют в уве-
личении проводимости (значение
(
)
xP выше, чем σ(x)/σ(1)). Для объяснения
введем понятия ячеек, принадлежащих скелету бесконечного кластера, и яче-
ек, лежащих на «мертвых концах». Для ячеек, находящихся на «мертвых
концах» возможно удаление в бесконечность только в одном направлении.
Рис
. 2.1.
Зависимости
мощности
бесконечного
кластера
и
приведенной
проводимости
от
доли
проводящих
ячеек
в
системе
(
)
xP
(
)
(
)
1σσ x
(
)
xP
(
)
(
)
1σσ x
0
1
с
x
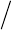
22
Такие
ячейки
,
входя
в
состав
бесконечного
кластера
,
увеличивают
значение
(
)
xP , но не влияют на значение
(
)
(
)
1σσ x .
С
материаловедческой
точки
зрения
применение
теории
перколяции
представляет
интерес
для
анализа
свойств
композитов
,
состоящих
не
только
из
«
проводящих
»
и
«
диэлектрических
»
ячеек
,
но
и
компонентов
,
составляю
-
щих
пары
«
проводник
–
сверхпроводник
», «
парамагнетик
–
магнетик
», «
па
-
раэлектрик
–
сегнетоэлектрик
»
и
др
.
С
теоретической
точки
зрения
модели
перколяции
разбивают
на
«
реше
-
точные
»
и
«
непрерывные
».
Решеточные
задачи
,
в
свою
очередь
,
разделяются
на
задачи
«
узлов
» (site problem)
и
«
связей
» (bond problem)
и
смешанные
зада
-
чи
(site-bond problem).
Задача
узлов
сводиться
к
нахождению
порога
проте
-
кания
на
решетке
с
заданными
параметрами
(
симметрия
,
размерность
про
-
странства
).
При
этом
анализируются
кластеры
,
образованные
контактирую
-
щими
узлами
–
сферами
(
например
, «
проводящими
»)
при
замещении
исход
-
ных
«
непроводящих
»
сфер
.
В
задаче
связей
все
исходные
узлы
–
сферы
,
расположенные
в
заданной
решетке
,
считаются
проводящими
,
но
контакт
между
ними
зависит
от
нали
-
чия
связей
.
В
задаче
связи
блокировка
узла
в
целом
осуществляется
при
раз
-
рыве
всех
связей
.
Разработаны
принципы
геометрии
«
покрывающих
»
реше
-
ток
,
демонстрирующих
соотношение
между
значениями
порогов
протекания
в
задаче
связей
(
)
св
c
x и задаче узлов
(
)
уз
c
x :
(
)
св
c
x ≤
(
)
уз
c
x .
Для прекращения протекания необходимо полностью блокировать опре-
деленную долю узлов, разорвав все связи, при этом остальная часть узлов
будет иметь некоторые разорванные связи. К настоящему времени найдены
значения порогов протекания для решеток в пространствах различной раз-
мерности d (d = 1, 2, 3 и др.), включая d = ∞ (решетки Бете). Решетки в про-
странствах d > 3, например, d = 6, представляют интерес для оценки перколя-
ционных явлений тензорных физических величин.
В табл. 2.1 приведены значения порогов протекания и связанных с ними
величин для двумерных и трехмерных решеток. Из табл. 2.1 видно, что зна-
чения порогов протекания существенно зависят от симметрии решетки и
размерности пространства d. Однако в задаче связей произведение
(
)
св
c
zx
(
z
–
координационное
число
ближайших
соседей
)
практически
не
зависит
от
симметрии
решетки
и
определяется
размерностью
пространства
d.
Для
задачи
узлов
такими
же
свойствами
обладает
произведение
(
)
уз
c
fx ,
23
где
f
–
доля
объема
(
площади
)
узла
в
элементарной
ячейке
.
Аналитические
решения
для
определения
c
x найдены только для четырех случаев двумер-
ных решеток (см. табл. 2.1).
Таблица 2.1
Размер
-
ность
,
d
Тип
решетки
Задача
узлов
Задача
связей
x
c
(
)
уз
f
(
)
(
)
узуз
c
fxI =
(
)
св
c
x
z
(
)
(
)
свсв
c
zxI
=
2
Квадратная
0.59 0.79 0.47
0.5
*
4 2
Треугольная
0.5
*
0.91 0.46
0.35
*
6 2.1
Медовые
соты
0.7 0.61 0.43
0.65
*
3 2
3
Тип
алмаз
0.43 0.34 0.15 0.39 4 1.56
Простая
кубическая
0.31 0.52 0.16 0.25 6 1.5
Объемно
-
центрированная
0.25 0.68 0.17 0.18 8 1.44
Гранецентрированная
0.2 0.74 0.15 0.12 12 1.44
* −
аналитические
решения
x
c
найдены
только
для
четырех
случаев
двумерных
решеток
.
Алгоритм
нахождения
c
x остальных задач включает процедуру оценки
случайных значений доли
ci
x
~
, при которых образуется стягивающий кластер
на заданной решетке с известным количеством узлом (например, для d = 2 на
квадратной решетке из
i
i
NN
×
узлов
),
усреднение
ci
x
~
для решетки
i
i
NN
×
,
нахождение
подобных
усредненных
значений
ci
x
~
для решеток с большим
числом узлов N и анализ зависимости усредненных значений
)(
~
NNc
x
×
от
N:
ν
)()(
~
N
D
xx
cNNc
+=
∞×
.
Если
полученные
результаты
удовлетворительно
описываются
приве
-
денной
зависимостью
(
т
.
е
.
значения
D
и
ν
положительны
),
то
определение
)(∞c
x
не
вызывает
затруднений
.
Смешанная
задача
(site-bond problem)
решается
на
решетках
,
в
которых
варьируются
доли
«
проводящих
»
и
«
непроводящих
»
узлов
и
доли
разорван
-
ных
и
целых
связей
.
Два
проводящих
узла
принадлежат
к
одному
и
тому
же
проводящему
кластеру
,
если
они
соединены
связью
.
Если
все
узлы
– «
проводящие
»,
задача
сводится
к
задаче
связей
.
Если
все
связи
не
разорваны
,
а
узлы
в
решетке
об
-
ладают
«
проводящими
»
и
«
непроводящими
»
свойствами
,
то
задача
сводиться

24
к
задаче
узлов
.
В
общем
виде
существует
критическая
кривая
на
плоскости
в
координатах
(
)
уз
c
x
и
(
)
св
c
x ,
разделяющая
фазовые
состояния
системы
.
Модель
site-bond
перколяции
наиболее
соответствует
образованию
геля
в
разбавленных
растворах
.
Рассмотрим
перколяционные
задачи
на
случайных
узлах
.
Переход
к
ре
-
шению
задач
со
случайным
распределением
узлов
–
существенный
шаг
в
ис
-
следовании
неоднородных
сред
.
В
теории
перколяции
ограничения
на
фик
-
сированные
положения
узлов
регулярной
решетки
снимаются
путем
рас
-
смотрения
изменения
перколяционных
параметров
при
взаимодействии
узла
с
узлами
не
только
первой
координационной
сферы
,
но
и
более
дальних
.
Физической
основой
такой
модели
может
служить
эффективное
взаимо
-
действие
магнитного
атома
не
только
с
ближайшими
соседями
,
но
и
с
атома
-
ми
из
более
удаленных
координационных
сфер
.
Из
анализа
результатов
,
сведенных
в
табл
. 2.2,
следует
,
что
значения
по
-
рога
протекания
(
)
уз
c
x
при
распространении
взаимодействия
на
более
уда
-
ленные
координационные
сферы
уменьшается
,
а
произведение
(
)
уз
c
zx
стре
-
мится
к
некоторым
постоянным
значениям
c
B ,
не
зависящим
от
симметрии
решетки
.
Заметим
,
что
для
гранецентрированной
кубической
(
ГЦК
)
решетки
чис
-
ло
возможных
расположений
взаимодействующих
узлов
только
в
первых
трех
координационных
сферах
уже
равно
42.
Значения
c
B
стремится
к
пре
-
делу
:
(
)
узlim
c
z
c
zxB
∞→
=
.
Для
простых
решеток
1,07,2
2
±
=
=d
c
B ,
для
объемных
3=d
c
B
=
= 4,1 ± 0,4.
Значения
c
B
определяют
возникновение
порога
протекания
.
Это
легко
показать
в
рамках
модели
охватывающих
сфер
(
окружностей
).
Под
охватывающими
сферами
понимают
перекрывающиеся
сферы
(
ок
-
ружности
).
Две
сферы
(
окружности
)
являются
связанными
,
если
центр
одной
сферы
(
окружности
)
находится
внутри
другой
.
Тогда
при
заданной
концен
-
трации
сфер
(
окружностей
)
N
можно
найти
перколяционный радиус
c
r
,
при
котором
достигается
порог
протекания
.
Для
задания
значения
c
r
можно
оп
-
ределить
необходимые
значения
концентраций
N
:
3
3
π
3
4
c
d
c
NrB
=
=
и

25
2
2
π
c
d
c
NrB
=
=
.
Необходимо
помнить
,
что
физические
величины
концентра
-
ций
N
имеют
различную
размерность
для
двумерного
и
трехмерного
случаев
.
Таблица
2.2
Тип
решетки
;
координационные
сферы
Число
соседей
z
Порог
протекания
x
c
(
)
уз
zx
c
(
)
уз
Плоские
Медовые
соты
; 1 3 0,7 2,1
Квадратная
; 1 4 0,59 2,36
Треугольная
; 1 6 0,5 3
Квадратная
; 1, 2 8 0,41 3,28
Треугольная
; 1, 2 12 0,295 3,54
Шестиугольная
; 1, 2, 3 12 0,3 3,6
Квадратная
; 1, 2, 3 12 0,292 3,5
Треугольная
; 1, 2, 3 18 0,225 4,05
Объемные
Тип
алмаз
; 1 4 0,425 1,7
ПК
; 1 6 0,307 1,84
ОЦК
; 1 8 0,243 1,94
ГЦК
; 1 12 0,195 2,34
ОЦК
; 1, 2 14 0,175 2,45
ПК
; 1, 2 18 0,137 2,47
ГЦК
; 1, 2 18 0,136 2,45
ПК
; 1, 2, 3 26 0,097 2,52
ОЦК
; 1, 2, 3 26 0,095 2,47
ГЦК
; 1, 2, 3 42 0,061 2,56
Теория
перколяции
успешно
используется
в
физике
полупроводников
.
На
ее
основе
развиты
теоретические
представления
о
переходе
«
металл
–
ди
-
электрик
»,
о
поведении
компенсированных
полупроводников
,
механизмах
прыжковой
проводимости
и
др
.
В
континуальных
задачах
теории
перколяции
узлы
вообще
не
рассмат
-
риваются
,
а
связанными
или
несвязанными
считаются
некоторые
области
пространства
.
Для
формирования
континуальной
задачи
вводится
непрерыв
-
ная
случайная
функция
V
(
r
).
Если
сопоставить
каждой
точке
r
случайное
число
,
никак
не
связанное
с
соседним
случайным
числом
,
получим
разрыв
-
ную
функцию
– «
белый
шум
».
Усреднение
белого
шума
по
сфере
радиуса
0
r
вокруг
данной
точки
дает
непрерывную
гауссову
случайную
функцию
.
Вели
-
чина
0
r
называется
радиусом
корреляции
случайных
функций
.

26
Если
гауссова
функция
построена
симметрично
(
средняя
по
пространст
-
ву
величина
0
=
V
),
то
она
характеризуется
гауссовым
распределением
с
дисперсией
σ
:
−=
2
2
σ2
exp
πσ2
1
)(
V
Vf .
При формулировке задачи протекания удобно разделять пространства на
два вида – «белое» и «черное». Пусть «белое» пространство то, где функция
(
)
rV меньше некоторого заданного числа
.
V
′
Тогда остальная часть про-
странства – «черное» пространство.
Посмотрим, что будет происходить при возрастании значения
.
V
′
Со
-
поставим
наши
представления
с
«
всемирным
потопом
».
Двумерная
модель
поверхности
имеет
впадины
и
вершины
.
При
увеличении
уровня
«
воды
» (
V
′
)
вначале
появляются
«
лужицы
»,
затем
«
озера
»,
которые
соединяются
канала
-
ми
,
наконец
,
при
некотором
значении
V
′
возникает
«
водяная
гладь
»,
по
ко
-
торой
можно
пересечь
пространство
«
водным
путем
».
Тогда
отношение
площади
зеркала
воды
к
общей
площади
соответствует
порогу
протекания
с
x ,
а
значение
V
′
(
уровень
воды
)
уровню
протекания
с
V .
Для
выбранной
функции
из
симметрийных
соображений
на
плоскости
всегда
есть
протекание
либо
по
«
белому
»,
либо
по
«
черному
»
пространству
.
Но
появление
протекания
по
«
белому
»
пространству
приводит
к
исчезнове
-
нию
протекания
по
«
черному
»
пространству
,
и
наоборот
.
Таким
образом
,
5,0
=
с
x .
Аналогично
из
симметрийных
соображений
0
=
с
V .
В
трехмерном
пространстве
каналы
протекания
по
«
белому
»
и
«
черно
-
му
»
пространствам
могут
быть
развязаны
(
подобно
развязке
дорог
через
виа
-
дук
).
Если
через
x
обозначить
долю
«
белого
»
пространства
,
а
с
x –
порог
протекания
по
«
белому
»
пространству
( 01,016,0
3
±
=
=
d
c
x ),
то
одновремен
-
ное
протекание
по
«
белому
»
и
«
черному
»
пространствам
будет
наблюдаться
при
с
x
<
x
<
с
x
−
1 .
Основной
задачей
теории
перколяции
является
исследование
поведение
системы
вблизи
порога
протекания
(
с
xx
−
<< 1).
Функции
,
характеризующие
перколяционный
переход
при
приближении
порога
протекания
,
изменяются
в
степенной
зависимости
от
расстояния
до
порога
.
Показатели
степени
носят
название
критических
индексов
.
Важней
-
шим
параметром
является
критический
индекс
радиуса
корреляции
.
ν

27
Зависимость
радиуса
корреляции
от
x
вблизи
порога
протекания
по
обе
стороны
характеризуется
симметричной
функцией
ν
−
−=
c
xxbL ,
где
b
–
длина
по
порядку
величины
,
близкая
к
периоду
решетки
.
Кроме
критическо
-
го
индекса
радиуса
корреляции
ν
в
теории
перколяции
важными
являются
критические
индексы
плотности
бесконечного
кластера
β
:
(
)
xP ~
(
)
β
c
xx −
и
критический
индекс
γ
среднего
числа
узлов
в
кластере
S
:
(
)
xS ~ .
γ
−
−
c
xx
Значения
критических
индексов
вблизи
перколяционного
перехода
сведены
в
табл
. 2.3.
Значения
критических
индексов
γ
,
υ
,
β
–
универсальны
.
Они
не
зависят
от
симметрии
решетки
и
от
типа
задач
и
определяются
только
размерностью
пространства
.
Это
свойство
характерно
для
теории
фазовых
переходов
,
по
-
этому
перколяционный
переход
часто
называют
геометрическим
фазовым
переходом
.
С
математической
точки
зрения
перколяционный
переход
анало
-
гичен
фазовому
переходу
второго
рода
.
При
этом
доля
«
проводящих
» («
магнитных
»
и
др
.)
узлов
(
связей
)
x
игра
-
ет
роль
температуры
,
мощность
бесконечного
кластера
(
)
xP
аналогична
па
-
раметру
порядка
,
средний
размер
кластера
(
)
xS
в
случае
магнитных
перехо
-
дов
аналогичен
восприимчивости
,
корреляционный
радиус
(
)
xL
имеет
оди
-
наковый
смысл
в
обоих
случаях
.
Значения
критических
индексов
для
двумерных
систем
получены
анали
-
тическим
путем
,
поэтому
в
табл
. 2.3
представлены
в
виде
дробей
.
Обратим
внимание
,
что
в
точке
перколяционного
перехода
функции
(
)
xL
и
(
)
xS
стремятся
к
бесконечности
,
а
функция
(
)
xP
обращается
в
ноль
.
Другими
словами
функции
(
)
xL
и
(
)
xS
имеют
симметричный
вид
относительно
точ
-
ки
перколяционного
перехода
c
x .
Поясним
физически
смысл
поведения
функций
(
)
xP ,
(
)
xL
и
(
)
xS .
При
случайном
характере
замещения
«
непроводящих
»
узлов
(
связей
) «
проводя
-
щими
»
с
ростом
доли
«
проводящих
»
узлов
(
связей
)
будут
возникать
одиноч
-
ные
«
проводящие
»
узлы
(
связи
)
и
объединяющие
их
кластеры
.
При
значении
c
x
возникает
перколяционный
кластер
,
пронизывающий
всю
систему
.
Мощ
-
ность
этого
бесконечного
кластера
(
)
xP
становится
отличной
от
нуля
и
воз
-
28
растает
вплоть
до
1
при
1
→
x
(
рис
. 2.1).
Только
вблизи
точки
перколяцион
-
ного
перехода
(
с
xx
−
<< 1)
наблюдается
степенная
зависимость
(
)
xP ~
( )
.
β
c
xx −
Рост
линейных
размеров
критических
(
больших
)
кластеров
от
0 < x <
c
x
характеризуется
функцией
(
)
.xL
Размер
критических
кластеров
стремится
к
бесконечности
при
приближении
значений
x
к
c
x .
При
перколя
-
ционном
переходе
возникает
один
бесконечный
кластер
(
)
xP
и
остается
множество
других
кластеров
меньших
размеров
.
Среднее
число
узлов
в
кла
-
стере
(
)
xS
имеет
подобный
вид
зависимости
от
значения
x
.
При
малом
уда
-
лении
от
порога
перколяции
с
xx
−
<< 1
вид
бесконечного
кластера
изменя
-
ется
,
образуется
сеткообразная
структура
,
обусловленная
присоединением
к
бесконечному
кластеру
(
)
xP
частей
,
ранее
представлявших
самостоятель
-
ные
ограниченные
кластеры
.
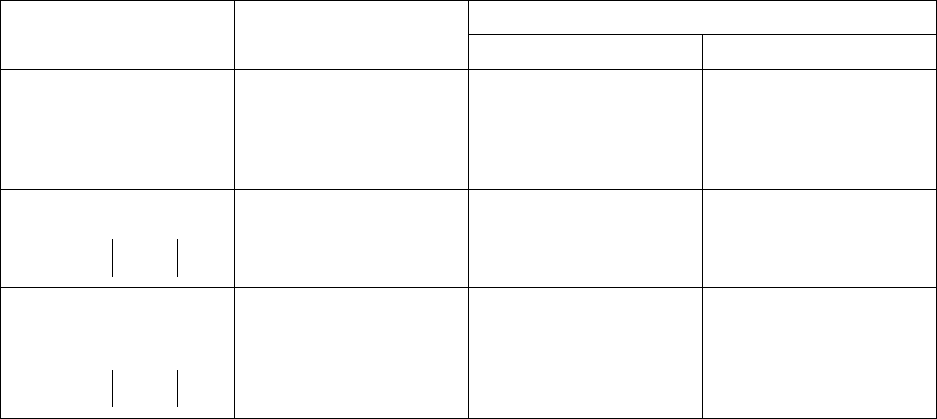
Таблица 2.3
Функция Критический индекс
Значение критического индекса
d = 2 d = 3
Мощность беско-
нечного кластера
(
)
xP ~
( )
β
c
xx
−
β
5/36 0,417
Радиус корреляции
(
)
xL ~
ν−
−
c
xx
ν
4/3 0,875
Среднее число уз-
лов в кластере
(
)
xS ~
γ−
−
c
xx
γ
43/18 1,795
Первоначальное
присоединение
(
только
одна
связь
)
между
кластерами
соответствуют
«
мертвому
»
концу
и
не
влияет
на
изменение
проводимости
.
В
дальнейшем
образуется
все
более
плотная
сетка
,
размеры
ячеек
которой
уменьшаются
.
Внутри
ячеек
остаются
изолированные
кластеры
.
Размеры
ячеек
сети
уменьшаются
с
дальнейшим
ростом
(
)
xP .
Корреляционная
длина
(
)
xL
и
средний
размер
кластера
(
)
xS
уменьшаются
.
Поскольку
размеры
ко
-
нечных
(
внутриячеистых
)
кластеров
,
изолированных
от
бесконечного
кла
-
стера
,
предопределяются
размерами
ячеек
,
часто
определяют
функцию
(
)
xL
как
функцию
,
несущую
информацию
о
размерах
больших
кластеров
до
точки

29
перколяционного
перехода
и
размеров
ячеек
сетки
после
перколяционного
перехода
.
Напомним
,
что
только
в
окрестности
c
xx
=
используются
степен
-
ные
зависимости
(
)
xL ~
ν
−
−
c
xx
и
(
)
xS ~ .
γ
−
−
c
xx
Зная
значения
критических
индексов
ν
,
γ
,
β
,
можно
оценить
критиче
-
ские
индексы
других
физических
явлений
в
неупорядоченных
средах
.
На
-
пример
,
компьютерные
расчеты
дают
для
зависимости
электропроводности
(
)
(
)
t
c
xxx −=
0
σσ , где
0
σ –
коэффициент
,
по
порядку
величины
близкий
к
значению
удельной
электропроводимости
кристаллической
решетки
со
всеми
проводящими
узлами
(
1
=
x
),
а
t
–
критический
индекс
электропроводности
( 3,1
2
=
t
для
размерности
пространства
d
= 2
и
7,1...6,1
3
=
t
для
d
= 3).
Найдем
зависимость
(
)
x
σ из модели одножильной сетки. Заменим не-
правильную и неупорядоченную скелетную сеть близкой идеальной решет-
кой (квадратной для
d
= 2,
кубической
для
d
= 3).
При
этом
период
решетки
будет
равен
радиусу
корреляции
L
.
Для
трехмерного
пространства
(
d
= 3)
удельная
электропроводность
(
)
x
σ такой идеализированной решетки равна
проводимости куба с единичной длиной ребра.
Число параллельно соединенных проволок, проходящих через грань
единичного куба, равно
.
2
−
L
Окончательно получаем:
(
)
xσ ~
2
−
L
~
(
)
.
ν
2
c
x
x −
Для двумерных случаев (d = 2) аналогичным путем получаем
(
)
xσ ~
1
−
L
~
(
)
.
ν
c
x
x −
Таким образом, критический индекс электропроводности t равен для
двумерных систем 34ν
2
=
=
=
tt ;
для
трехмерного
случая
75,1ν2
3
=
=
=
tt
(
см
.
табл
. 2.3).
При
рассмотрении
перколяционных
систем
часто
констатиру
-
ется
,
что
перколяционный
кластер
имеет
фрактальную
структуру
.
В
рамках
теории
перколяции
найдена
связь
массовой
фрактальной
размерности
D
с
универсальными
критическими
индексами
:
D = d – β/ν.
Например
,
для
двумерного
пространства
D = 91/48,
для
трехмерного
пространства
(d = 3)
находим
D ≈ 2,54.
Но
при
этом
надо
понимать
,
что
фрак
-
30
тальность
сохраняется
в
интервале
корреляционного
радиуса
(
)
.xL
Другими
словами
,
в
точке
перколяционного
перехода
c
xx
=
весь образец является
фракталом. С удалением от точки перколяционного перехода размеры
(
)
xL
быстро уменьшаются и фрактальность сохраняется только в меньших мас-
штабах. При экспериментальном определении фрактальной размерности D
необходимы методы с локальностью более высокой, чем текущее значение
(
)
.xL
При
больших
масштабах
сформированный
бесконечный
кластер
может
считаться
гомогенным
и
состоящим
из
ячеек
размером
(
)
.xL
2.2.
Описание
программы
«
Перколяция
»
В
работе
проводится
компьютерное
моделирование
образования
перко
-
ляционного
кластера
в
задаче
узлов
на
двумерной
решетке
.
Параметрами
,
определяющими
условия
роста
кластера
,
являются
тип
и
количество
узлов
решетки
,
а
также
число
учитываемых
координационных
сфер
.
На
рис
. 2.2
приведено
изображение
интерфейса
программы
с
примерами
перколяционных
кластеров
на
решетках
с
различным
числом
ближайших
со
-
седей
.
Выбрав
тип
и
размер
решетки
,
можно
увидеть
образующийся
перко
-
ляционный
кластер
и
порог
протекания
–
ту
долю
от
единицы
,
что
составля
-
ют
интересующие
нас
частицы
,
образующие
перколяционный
кластер
.
Поясним
на
конкретном
примере
.
Все
частицы
разделены
на
белые
и
черные
.
Существует
небольшая
доля
черных
частиц
.
Определим
,
при
какой
доле
черных
частиц
образуется
кластер
из
соседствующих
черных
частиц
,
пересекающий
все
имеющееся
пространство
.
Имеем
несколько
черных
час
-
тиц
на
левом
крае
и
начинаем
искать
соседние
черные
.
Для
новых
черных
тоже
ищем
их
соседей
.
Таким
образом
,
продолжаем
до
тех
пор
,
пока
все
чер
-
ные
,
которые
соприкасаются
с
первоначальными
на
левом
крае
,
в
том
числе
и
через
другие
черные
,
не
будут
обнаружены
.
Итак
,
имеем
большие
класте
-
ры
,
или
кластер
,
с
несколькими
точками
на
левом
крае
.
Если
этот
кластер
имеет
точки
,
или
хотя
бы
одну
,
на
правом
крае
,
то
это
–
перколяционный
кластер
,
пронизывающий
всю
плоскость
.
Доля
черных
в
общем
количестве
и
есть
порог
протекания
.
Примером
из
практики
может
служить
островковая
проводимость
.
Имея
проводящие
включения
в
диэлектрике
при
подаче
поля
,
мы
можем
иметь
пробой
за
счет
перескакивания
носителей
с
островка
на
соседний
.
Порог
протекания
и
будет
необходимой
долей
проводящих
включений
,
при
которых
