Наноматериалы: лабораторный практикум под ред. В.А. Мошникова

Подождите немного. Документ загружается.

МИНОБРНАУКИ РОССИИ

_________________________

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

_____________________________________

НАНОМАТЕРИАЛЫ

Лабораторный практикум

Санкт-Петербург

Издательство СПбГЭТУ «ЛЭТИ»

2010

УДК 612.3.049.77.002.3(07)

ББК Ж 37я7

Н25

Авторы: И. Е. Грачева, А. В. Гузь, А.А. Кальнин, С. С. Карпова,

М. Г. Кунгуров, Л. Б. Матюшкин, В. А. Мошников, А. А. Пономарева,

Ю. М. Спивак.

Наноматериалы: лабораторный практикум / Под ред. В. А. Мошнико-

ва. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2010. 93 с.

ISBN 978-5-7629-1118-4

Дано описание лабораторно-практических работ по образованию фрак-

талов, золь-гель-технологии, атомно-силовой микроскопии, измерению газо-

чувствительных структур с иерархией пор, анализу удельной поверхности

порошковых и пористых материалов методом тепловой десорбции, исследо-

ванию перколяционных переходов и нанокомпозитов с магнитными капсу-

лированными наночастицами со значениями концентрации до и после порога

протекания.

Предназначен для проведения лабораторных работ по дисциплинам

«Материаловедение микро- и наносистем», «Наноматериалы» для подготов-

ки магистров по направлениям «Электроника и микроэлектроника» и «Нано-

технология».

УДК 612.3.049.77.002.3(07)

ББК Ж 37я7

Рецензенты: кафедра ПФОТТ СПбГПУ; д-р физ.-мат. наук, проф.

С. Ю. Давыдов (ФТИ им. А. Ф. Иоффе РАН).

Утверждено

редакционно-издательским советом университета

в качестве учебного пособия

ISBN 978-5-7629-1118-4 © CПбГЭТУ «ЛЭТИ», 2010

ПРЕДИСЛОВИЕ

Цикл лабораторных работ предназначен для получения навыков и уг-

лубленного понимания процессов, происходящих при образовании наноком-

позитов. Композитные материалы используются при создании новых уст-

ройств фотоники, электроники, водородной энергетике, катализа.

Вклад каждого члена коллектива в лабораторный практикум:

Лабораторная работа 1: Матюшкин Л. Б., Кунгуров М. Г.

Лабораторная работа 2: Гузь А. В., Мошников В. А.

Лабораторная работа 3: Гузь А. В., Мошников В. А.

Лабораторная работа 4: Гузь А. В., Мошников В. А.

Лабораторная работа 5: Грачева И. Е., Карпова С. С.

Лабораторная работа 6: Грачева И. Е., Пономарева А. А.

Лабораторная работа 7: Карпова С. С., Мошников В. А., Грачева И. Е.

Лабораторная работа 8: Спивак Ю. М., Мошников В. А.

Лабораторная работа 9: Кальнин А. А.

Лабораторный практикум предназначен для магистерской подготовки по

программам «Микро- и наносистемная техника» и «Нанотехнология и диаг-

ностика».

Компьютерные лабораторные работы могут быть эффективно использо-

ваны для самоподготовки и повышения квалификации специалистов в про-

цессе непрерывного образования.

Лабораторная работа 1

РАСЧЕТ ЗОННОЙ СТРУКТУРЫ НАНОТРУБОК

МЕТОДОМ ЛКАО

Цель работы: ознакомление со строением нанотрубок, применением

метода ЛКАО для полимеров и использованием его в исследовании закона

дисперсии для различных видов нанотрубок.

1.1. Основные понятия и определения

1.1.1. Коэффициенты хиральности

Не содержащая дефектов одностенная углеродная нанотрубка представ-

ляет собой свернутую в виде цилиндра ленту с упаковкой атомов по типу

графита.

а б в

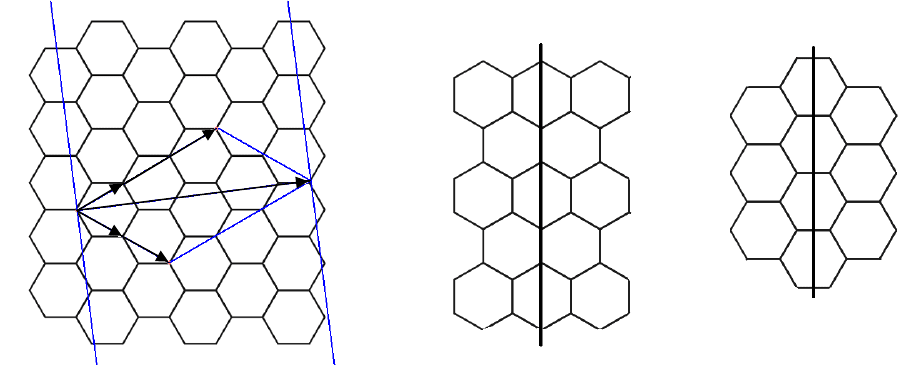
Рис. 1.1. Построение структурной модели: a – часть графитового слоя, из которого

вырезается лента, сворачиваемая в трубк у; фрагменты нанотрубок «зигзаг» (б)

и «кресло» (в) относительно образующей L

Чтобы представить пространственное расположение атомов в иде-

альной однослойной нанотрубке, отложим на графитовом слое вектор С =

+ ma

, где a

и a

– базисные векторы, а n и m – целые числа (рис.

1.1). Через концы вектора C проведем перпендикулярно ему две прямые –

L и L' и вырежем из слоя бесконечную ленту вдоль этих линий. Свернем

ленту в цилиндр так, чтобы прямые L и L' совместились. У этого цилинд-

ра L будет образующей, а длина окружности равна модулю вектора C. Так

мы получили структурную модель нанотрубки (n, m). Такая нанотрубка

не образует швов при сворачивании.

С = na

+ ma

В общем случае нанотрубки обладают винтовой осью симметрии (то-

гда говорят, что они хиральны). Нехиральными называются нанотрубки (n, 0)

и (n, n), в которых углеродные шестиугольники ориентированы, соответст-

венно, параллельно и перпендикулярно оси цилиндра (рис. 1.1, б, в). По

внешнему виду поперечного среза нанотрубки (n, 0) называют нанотрубками

«зигзаг» (zigzag), а нанотрубки (n, n) – нанотрубками типа «кресло»

(armchair).

Индексы хиральности нанотрубки (n, m) однозначным образом опреде-

ляют ее структуру, в частности, диаметр d. Эта связь имеет следующий вид:

2 2

d n m nm

= + +

, (1.1)

где

= 0,142

нм

–

расстояние

между

соседними

атомами

углерода

графи

товой

плоскости

1.1.2. Строение и электропроводность

Для

создания

электронных

устройств

их

объединения

сложные

при

боры

требуются

полупроводники

материалы

высокой

электропроводно

стью

Нанотрубки

разными

значениями

индексов

(

) –

это

полимеры

разного

строения

потому

они

должны

обладать

разными

электрическими

свойствами

Зависимости

электрических

свойств

нанотрубок

от

геометриче

ских

параметров

были

предсказаны

на

основе

квантово

химических

расчетов

их

зонной

структуры

независимо

фактически

еще

до

экспериментального

обнаружения

нанотрубок

Отметим

что

все

атомы

углерода

нанотрубках

имеют

тройную

коор

динацию

три

из

четырех

валентных

электронов

каждого

углерода

образуют

гибридные

орбитали

локализованные

связи

C – C,

четвертый

участ

вует

образовании

делокализованной

системы

(

как

графите

или

бензоле

Эти

электроны

слабо

связаны

со

своими

атомами

поэтому

именно

они

уча

ствуют

переносе

заряда

системе

Высокая

проводимость

должна

появить

ся

если

занятые

состояния

не

отделены

энергетической

щелью

от

вакант

ных

состояний

противном

случае

нанотрубка

–

полупроводник

если

щель

малая

или

диэлектрик

если

большая

Расчеты

показывают

что

металлическим

типом

зонной

структуры

обла

дают

те

нанотрубки

для

которых

разность

n – m

кратна

трем

Остальные

на

нотрубки

должны

быть

полупроводниками

шириной

запрещенной

зоны

от

нескольких

десятых

до

примерно

одного

электрон

вольта

возрастающей

уменьшением

диаметра

нанотрубки

качестве

иллюстрации

расчета

электронной

структуры

выбран

метод

линейной

комбинации

атомных

орбиталей (ЛКАО

)

электронном

прибли

жении

приближении

функциональной

плотности

Положительными

сторо

нами

этого

метода

являются

его

наглядность

относительная

простота

Эти

качества

теряются

более

сложных

не

рассматриваемых

здесь

случаях

на

пример

метод

ЛКАО

не

вполне

пригоден

для

расчетов

электронной

струк

туры

нанотрубок

интеркалированных

атомами

тяжелых

элементов

напри

мер

переходных

металлов

Для

таких

случаев

используют

более

сложные

методы

например

метод

линеаризованных

присоединенных

цилиндриче

ских

волн

(

ЛПЦВ

1.1.3. Введение в метод линейной комбинации

атомных орбиталей (ЛКАО)

Согласно

положениям

квантовой

механики

электронное

строение

моле

кулы

как

системы

электронов

кулоновском

поле

ядер

пространственное

расположение

которых

известно

можно

определить

из

ее

многоэлектронной

волновой

функции

зависящей

от

координат

всех

электронов

Волновые

функции

дают

максимально

полную

информацию

об

электронной

систе

ме

молекулы

но

рассчитать

их

для

сложных

систем

например

нанотрубок

опираясь

только

на

уравнение

Шредингера

не

используя

никаких

физически

правдоподобных

предположений

характере

волновой

функции

многоэлек

тронной

системы

невозможно

Одно

из

важнейших

приближений

исполь

зуемых

теории

строения

многоэлектронных

систем

упрощающих

решение

уравнения

Шредингера

состоит

том

что

многоэлектронную

волновую

функцию

записывают

виде

детерминанта

построенного

из

одноэлектрон

ных

волновых

функций

1 1 2 2 1

1 2 2 2 2

1 2

( ) ( ) ... ( )

( , , ... , ) det .

... ... ... ...

( ) ( ) ... ( )

k N

N N N N

q q q

ϕ ϕ ϕ

Ψ =

ϕ ϕ ϕ

(1.2)

Физический смыл записи многоэлектронной волновой функции в виде

антисимметризованного произведения одноэлектронных волновых функций

состоит в том, что каждому электрону молекулы приписывается своя волно-

вая функция

, называемая спин-орбиталью. Каждая спин-орбиталь являет-

ся произведением функции Ψ

, y

, z

), зависящей только от пространст-

венных координат электрона, на спиновую функцию. Функция Ψ

называется

орбиталью. Для атомов это будет атомная орбиталь (АО), для молекул – мо-

лекулярная орбиталь (МО). В кристаллах или полимерах с трансляционной

симметрией функции Ψ

называют блоховскими функциями. Спиновая

функция может принимать два значения, отвечающие проекции спина на ось

z: +1/2 и –1/2. Представление волновой функции Ψ в виде определителя (1.2)

обеспечивает выполнение условия антисимметричности волновой функции

относительно перестановки электронов; перестановке электронов соответст-

вует перестановка строк в определителе (1.2), при этом он умножается на –1.

Множитель перед определителем необходим для нормировки много-

электронной функции; орбитали считаются нормированными:

1, 0 ï ðè .

d d

µ µ ν

ϕ ν = ϕ ϕ ν = µ ≠ ν

∫ ∫

Явный вид обитали Ψ

находится из одноэлектронного приближения

уравнения Шредингера:

H E

µ µ µ

Ψ = Ψ

= 1, 2, 3, …; (1.3)

+ ( ).

H U

= − ∆

Системы

уравнений

Хартри

–

Фока

(1.3)

решаются

помощью

метода

по

следовательных

приближений

поскольку

явный

вид

гамильтониана

зависит

от

вида

искомых

волновых

функций

Сущность

этого

метода

состоит

том

что

для

каждого

электрона

на

первом

этапе

подбирается

пробная

волно

вая

функция

помощью

которой

рассчитывается

оператор

Хартри

–

Фока

(

гамильтониан

)

решаются

уравнения

(1.3).

Полученные

более

точные

вол

новые

функции

подставляются

систему

уравнений

(1.3),

ее

решают

зано

во

Этот

процесс

продолжают

до

тех

пор

пока

энергии

вид

орбиталей

на

предыдущем

последующем

шаге

не

перестанут

различаться

Когда

это

достигнуто

полученное

решение

называют

самосогласованным

помощью

быстродействующих

ЭВМ

уравнения

Хартри

–

Фока

чис

ленной

форме

были

решены

для

всех

основных

атомов

ионов

результа

те

определен

вид

атомных

орбиталей

(

АО

)

их

энергии

Из

за

более

низкой

симметрии

многоатомных

систем

расчет

орбиталей

этом

случае

непосред

ственно

из

уравнений

Хартри

–

Фока

оказывается

существенно

более

трудо

емкой

задачей

чем

расчет

АО

атомов

Поэтому

здесь

используются

даль

нейшие

приближения

Стандартный

подход

состоит

том

что

искомые

ор

битали

разлагаются

по

базису

i i

µ µ

Ψ = χ

∑

(1.4)

где

–

функции

вид

которых

вообще

говоря

не

тривиален

разных

методах

различен

; n –

общее

число

включенных

базис

функций

; a

µi

–

коэффициенты

определяющие

вклад

базисной

функции

собственную

функцию

выражении

(1.4)

качестве

базиса

для

расчета

орбиталей

многоатом

ной

системы

используют

атомные

орбитали

теории

молекул

такой

подход

называют

методом

ЛКАО

теории

кристаллов

–

методом

сильной

связи

Первоначально

теория

электронного

строения

нанотрубок

развивалась

рам

ках

метода

ЛКАО

физической

точки

зрения

представление

МО

виде

ЛКАО

отвечает

предположению

том

что

окрестности

каждого

атома

где

влияние

потенциала

более

далеких

атомов

ослабевает

одноэлектронная

вол

новая

функция

молекулы

должна

походить

на

атомную

разложениях

(1.4)

можно

использовать

численные

хартри

фоковские

АО

или

проводить

вычис

ления

аналитическими

функциями

имеющими

явную

запись

виде

фор

мул

но

которые

хорошо

аппроксимируют

хартри

фоковские

АО

Впрочем

конкретный

вид

АО

нам

здесь

не

потребуется

1.1.4. Симметрия полимеров

Отличие

нанотрубок

от

малых

молекул

конечно

состоит

том

что

на

нотрубка

–

это

полимер

система

состоящая

из

очень

большого

числа

атомов

–

порядка

числа

Авогадро

Расчеты

электронной

структуры

полиме

ров

удобно

проводить

предположении

том

что

число

атомов

полимере

бесконечно

что

они

образуют

структуру

повторяющуюся

одном

направ

лении

–

вдоль

трансляционной

оси

такой

точки

зрения

полимер

–

это

од

номерный

кристалл

Такой

подход

позволяет

понизить

размерность

секуляр

ного

уравнения

метода

ЛКАО

от

числа

базисных

атомных

орбиталей

поли

мере

до

их

числа

элементарной

ячейке

Элементарная

ячейка

–

это

минимальный

фрагмент

трансляцией

кото

рого

воспроизводится

вся

структура

полимера

качестве

простейшего

по

лимера

представим

себе

линейную

цепочку

из

атомов

углерода

одинаковы

ми

расстояниями

между

атомами

Это

будет

полимер

одним

атомом

каж

дой

ячейке

Размер

элементарной

ячейки

длина

вектора

элементарной

трансляции

здесь

будут

равны

расстоянию

между

атомами

Совокупность

векторов

= l

(l = 0, ±1, ±2, …)

образует

прямую

решетку

одномерной

пе

риодической

системы

элементарной

ячейке

может

быть

несколько

атомов

Например

если

только

что

рассмотренной

цепочке

чередуются

длинные

короткие

расстояния

между

атомами

то

это

будет

полимер

двумя

атомами

элементарной

ячейке

Такой

структурой

обладает

карбин

–

простейший

чисто

углеродный

нанопровод

элементарных

ячейках

нанотрубок

(5, 5)

(10, 0)

содержится

атомов

соответственно

Для

полимера

трансляционной

симметрией

направлении

гамильто

ниан

инвариантен

относительно

трансляций

( ) ( )

ˆ ˆ

H l H+ =

r c r

этом

случае

решение

уравнения

Шредингера

(1.3)

облегчается

тем

что

электронная

плотность ρ

(

)

также

является

периодической

функцией

вектора

трансляций

(

r +

) =

(

Как

известно

любую

периодическую

функцию

f(z)

можно

разложить

ряд

Фурье

( ) exp .

f z A i nz

 

 

 

∑

(1.5)

Определим

одномерную

обратную

решетку

как

совокупность

точек

на

оси

координатами

g n

расстоянием

между

точками

Соответственно

терминах

обратного

пространства

разложение

(1.5)

можно

переписать

несколько

более

ком

пактной

форме

которая

называется

разложением

ряд

по

обратной

решетке

(

)

( ) exp .

n n

f z A ig z

∑

Легко

убедиться

трансляционной

периодичности

функций

описываемых

этим

разложением

(

)

(

)

( )

( ) exp exp

exp exp 2 exp ( ).

n n n

n n n n

n n

f z lc A ig z ig lc

A ig z i nl A ig z f z

+ = =

= π = =

∑

∑ ∑

Коэффициенты разложения A

равны

( )

( )exp .

n n

A f z ig z dz

∫

В общем случае, Ψ(r + lc) ≠ Ψ(r): волновая функция полимера не являет-

ся периодической функцией трансляций. Однако из условий ρ(r) = |Ψ(r)|

периодичности распределения электронной плотности ρ(r) следует, что

квадрат волновой функции является функцией периодической, а значит

Ψ(r + lc) = e

Ψ(r), т. е. трансляция сопровождается умножением волновой

функции на фазовый множитель, по модулю равный единице. Этот множи-

тель обычно записывают в виде α = klc. Величина k является характеристи-

кой свойств симметрии волновой функции, и этой функции можно приписать

индекс k. Итак,

Ψ(r + lc) = e

iklc

Ψ(r).

Это уравнение называют теоремой Блоха. Величина k имеет размер-

ность обратную длине и определяется с точностью до постоянной обратной

решетки g

. Для определенности, значения величины k выбирают в интерва-

ле – π/с < k ≤ π/с (в так называемой первой зоне Бриллюэна для одноперио-

дической системы). Величину k называют волновым вектором или квазиим-

пульсом.

Иногда удобно считать, что полимер состоит из конечного, а не из бес-

конечного числа L повторяющихся элементов, а чтобы избежать влияния

концевых элементов, полагать, что полимер замкнут в кольцо так, что первая

ячейка соединена с последней. (В физике твердого тела этот прием известен

как циклические граничные условия Борна–Кармана). Тогда в результате L

трансляций система переходит сама в себя:

(r + lc) = e

ikLc

(r) = Ψ

(r).

Из условий Борна–Кармана следует, что k на интервале – π/с < k ≤ π/с

принимает L дискретных значений, отвечающих условию:

k m

, m = 0, ± 1, ± 2, …, ± L / 2.

Если L достаточно велико, например порядка числа Авогадро, то элек-

тронное строение бесконечной линейной цепочки и замкнутого кольца не

будет различаться.