Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

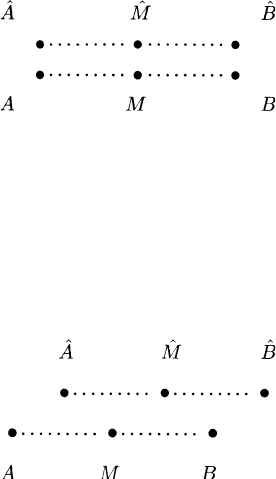
34 1 Geometrical Structure of M

by E

) and similarly B and

B coincide when E

occurs. At their convenience

the two observers O and

O presiding over S and

S respectively collect all

of the data recorded by their assistants for analysis. Each will inspect the

coordinates of the two marked points, calculate from them the coordinates

of the midpoint of the line segment joining these two points in his coordinate

system (denote these midpoints by M and

M) and inquire of his assistant

located at this point whether or not the light signals emitted from the two

explosions arrived simultaneously at his location. In general, of course, there

is no reason to expect an aﬃrmative answer from either, but let us just

suppose that in this particular case one of the observers, say O, ﬁnds that the

light signals from the two explosions did indeed arrive simultaneously at the

midpoint of the line segment joining the spatial locations of the explosions in



. According to the criteria we have established, O will therefore conclude

that E

and E

were simultaneous so that, from his point of view, A and

A, M and

M and B and

B all coincide “at the same time”.

Fig. 1.3.8

Continuing to analyze the situation as it is viewed from S we observe that, by

virtue of the ﬁnite speed at which the light signals propagate, a nonzero time

interval is required for these signals to reach M and that, during this time

interval, M and

M separate so that the signals cannot meet simultaneously

Fig. 1.3.9

Indeed, if the motion is as indicated in Figures 1.3.8 and 1.3.9, the light from

will clearly reach

M before the light from E

. Although we have reached

this conclusion by examining the situation from the point of view of O,any

other admissible observer will necessarily concur since we have assumed that

all such observers agree on the temporal order of any two events on the

1.3 The Lorentz Group 35

worldline of a photon (consider a photon emitted at E

and the two events

on its worldline corresponding to its encounters with

M and the light signal

emitted at E

). In particular,

O must conclude that E

occurred before E

and consequently that these two events are not simultaneous. When O and

next meet they compare their observations of the two explosions and discover,

much to their chagrin, that they disagree as to whether or not these two

events were simultaneous. Having given the matter some thought, O believes

that he has resolved the diﬃculty. The two events were indeed simultaneous

as he had claimed, but they did not appear so to

O because

O was moving

(running toward the light signal from E

and away from that of E

). To this

O responds without hesitation “I wasn’t moving — you were! The explosions

were not simultaneous, but only appeared so to you because of your motion

toward E

and away from E

”. This apparent impasse could, of course, be

easily overcome if one could determine with some assurance which of the two

observers was “really moving”. But it is precisely this determination which

the Relativity Principle disallows: One can attach no objective meaning to

the phrase “really at rest”. The conclusion is inescapable: It makes no more

sense to ask if the events were “really simultaneous” than it does to ask if O

was “really at rest”. “Simultaneity”, like “motion” is a purely relative term.

If two events are simultaneous in one admissible frame of reference they will,

in general, not be simultaneous in another such frame.

The relativity of simultaneity is not easy to come to terms with, but it

is essential that one do so. Without it even the most basic contentions of

relativity appear riddled with logical inconsistencies.

Exercise 1.3.22 Observer

O is moving to the right at constant speed β rel-

ative to observer O (along their common x

-, ˆx

-axes with origins coinciding

at x

=ˆx

= 0). At the instant O and

O pass each other a ﬂashbulb emits

a spherical electromagnetic wavefront. O observes this spherical wavefront

moving away from him with speed 1. After x

meters of time the wavefront

will have reached points a distance x

meters from him. According to O,at

the instant the light has reached point A in Figure 1.3.10 it has also reached

point B. H

ever,

O regards himself as at rest with O moving so he will also

observe a spherical wavefront moving away from him with speed 1. But as the

light travels to A,

O has moved a short distance to the right of O so that the

spherical wavefront observed by

O is not concentric with that observed by O.

In particular, when the light arrives at A,

O will contend that it also reaches

(not B yet, but) C. They cannot both be right. Resolve the “paradox”. Hint:

There is an error in Figure 1.3.10. Compare it with Figure 1.3.11 after you

ve ﬁlled in

the

blanks.

To be denied the absolute, universal notion of simultaneity which the

rather limited scope of our day-to-day experience has led us to accept uncriti-

cally is a serious matter. Disconcerting enough in its own right, this relativity

of simultaneity also necessitates a profound reevaluation of the most basic

concepts with which we describe the world. For example, since our observers

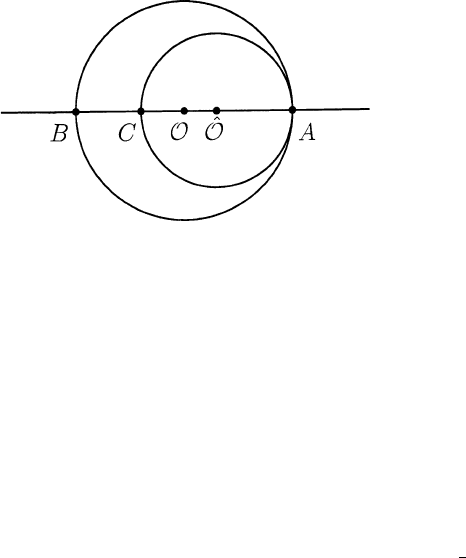
36 1 Geometrical Structure of M

Fig. 1.3.10

O and

O need not agree on the time lapse between two events even when one

of them measures it to be zero, one could scarcely expect them to agree on

the elapsed time between two arbitrarily given events. And, indeed, we have

already seen in (1.3.20)thatΔx

and Δˆx

are generally not equal. This eﬀect,

known as time dilation, has a particularly nice geometrical representation in

a Minkowski diagram (see Figure 1.3.12). E

(resp., E

)canbeidentiﬁed

physically with the appearance of the reading “1” on the clock at the origin

of S (resp.,

S). In S,E

is simultaneous with E

which corresponds to a

reading strictly less than 1 on the clock at the origin in

S. Since the clocks

at the origins of S and

S agreed at x

=ˆx

=0, O concludes that

O’s

clock is running slow. Indeed, (1.3.21)and(1.3.22) show that each observes

the other’s time dilated by the same constant factor γ =(1− β

)

−

.The

moral of the story, perhaps a bit too tersely stated, is that “moving clocks

run slow”.

Exercise 1.3.23 Pions are subatomic particles which decay spontaneously

and have a half-life (at rest) of 1.8 × 10

−8

sec (= 5.4m). A beam of pions

is accelerated to a speed of β =0.99. One would expect that the beam

would drop to one-half its original intensity after travelling a distance of

(0.99)(5.4m) = 5.3m. However, it is found experimentally that the beam

reaches one-half intensity after travelling approximately 38m. Explain! Hint:

Let S denote the laboratory frame of reference,

S the rest frame of the pi-

ons and assume that S and

S are related by (1.3.27)and(1.3.29). Draw a

Minkowski diagram which represents the situation.

Return for a moment to Figure 1.3.12 and, in particular, to the line ˆx

=1.

Each point on this line can be identiﬁed with the appearance of the reading

“1” on a clock that is stationary at some point in



.Thesealloccur“simul-

taneously” for

O because his clocks have been synchronized. However, each

of these events occurs at a diﬀerent “time” in S so O will disagree. Clocks at

diﬀerent locations in



read 1 at diﬀerent “times” so, according to O,they

cannot be synchronized.

Here is an old, and much abused, “paradox” with its roots in the phe-

nomenon of time dilation, or rather, in a basic misunderstanding of that

phenomenon. Suppose that, at (0, 0, 0, 0), two identical twins part company.

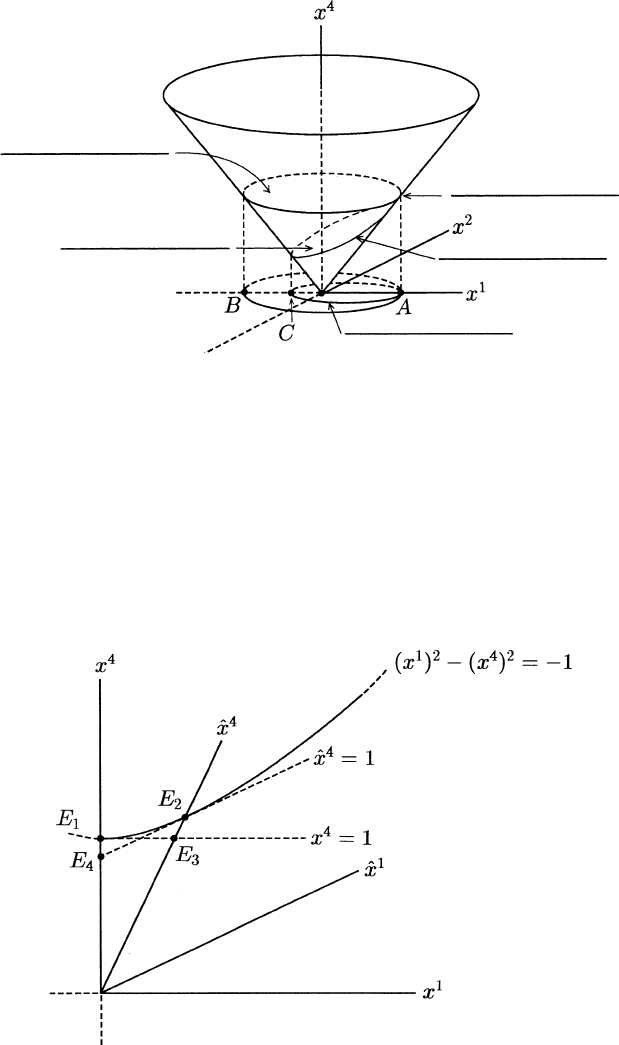
1.3 The Lorentz Group 37

Fig. 1.3.11

One remains at rest in the admissible frame in which he was born. The other

is transported away at some constant speed to a distant point in space where

he turns around and returns at the same constant speed to rejoin his brother.

At the reunion the stationary twin ﬁnds that he is considerably older than his

more adventurous brother. Not surprising; after all, moving clocks run slow.

However, is it not true that, from the point of view of the “rocket” twin, it

is the “stationary” brother who has been moving and must, therefore, be the

younger of the two?

Fig. 1.3.12

38 1 Geometrical Structure of M

The error concealed in this argument, of course, is that it hinges upon a

supposed symmetry between the two twins which simply does not exist. If

the stationary twin does, in fact, remain at rest in an admissible frame, then

his brother certainly does not. Indeed, to turn around and return midway

through his journey he must “transfer” from one admissible frame to another

and, in practice, such a transfer would require accelerations (slow down, turn

around, speed up) and these accelerations would be experienced only by the

traveller and not by his brother. Nothing we have done thus far equips us

to deal with these accelerations and so we can come to no conclusions about

their physical eﬀects (we will pursue this further in Section 1.4). That they

do have physical eﬀects, however, can be surmised even now by idealizing the

situation a bit. Let us replace our two twins with three admissible frames: S

(stationary twin),

S (rocket twin on his outward journey) and

S (rocket twin

on his return journey). What this amounts to is the assumption that the two

individuals involved compare ages in passing (without stopping to discuss it)

at the beginning and end of the trip and that, at the turnaround point, the

traveller “jumps” instantaneously from one admissible frame to another (he

cannot do that, of course, but it seems reasonable that, with a suﬃciently

durable observer, we could approximate such a jump arbitrarily well by a

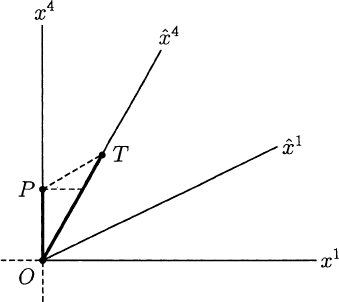
“large” acceleration over a “small” time interval). Figure 1.3.13 represents

the outward journey from O to the turnaround event T .

Fig. 1.3.13

Notice that, in

S,Tis simultaneous with the event P on the worldline

of the stay-at-home. In S,Pis simultaneous with some earlier event on the

worldline of the traveller. Each sees the other’s time dilated. Figure 1.3.14

represents the return journey. Notice that, in

S,Tis simultaneous with (not

P , but) the event Q on the worldline of the stationary twin, whereas, in S,Q

is simultaneous with some later event on the traveller’s worldline. Each sees

the other’s time dilated. Now, put the two pictures together in Figure 1.3.15

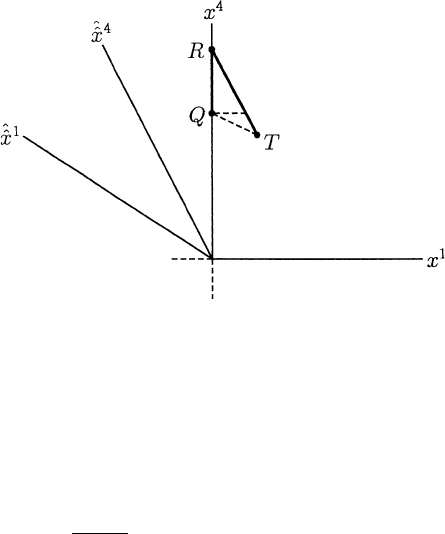
1.3 The Lorentz Group 39

Fig. 1.3.14

and notice that in “jumping” from

S to

S, our rocket twin has also jumped

over the entire interval from P to Q on the worldline of his brother; an interval

over which his brother ages, but he does not. The lesson to be learned is that,

while all motion is indeed relative, it is not all physically equivalent.

Exercise 1.3.24 Account, in a sentence or two, for the “missing” time in

Figure 1.3.15. Hint:

2β

1+β

>βfor 0 <β<1.

There is one last kinematic consequence of the relativity of simultaneity,

as interesting, as important and as surprising as time dilation. To trace its

origins we return once again to the explosions E

and E

,observedbyS and

S and discussed on pages 33–36. Recall that the points A in



and

A in



coincided when E

occurred, whereas B in



and

B in



coincided when E

occurred. Since the two events were simultaneous in S,theobserverO will

conclude that A coincides with

A at the same instant that B coincides with

B and, in particular, that the segments AB and

B have the same length

(see Figure 1.3.8). However, in

S,E

occurred before E

so B coincides

with

B before A coincides with

A and

O must conclude that the length

B is greater than the length of AB. More generally, two objects (say,

measuring rods) in relative motion are considered to be equal in length if,

when they pass each other, their respective endpoints A,

A and B,

B coincide

simultaneously. But, “simultaneously” according to whom? Here we have two

events (the coincidence of A and

A and the coincidence of B and

B)andwe

have seen that if one admissible observer claims that they are simultaneous

(i.e., that the lengths AB and

B are equal), then another will, in general,

disagree and we have no reason to prefer the judgment of one such observer to

that of another (Relativity Principle). “Length”, we must conclude, cannot

be regarded as an objective attribute of the rods, but is rather simply the

result of a speciﬁc measurement which we can no longer go on believing

must be the same for all observers. Notice also that these conclusions have

40 1 Geometrical Structure of M

nothing whatever to do with the material construction of the measuring rods

(in particular, their “rigidity”) since, in the case of the two explosions, for

example, there need not be any material connection between the two events.

This phenomenon is known as length contraction (or Lorentz contraction)

and we shall now look into the quantitative side of it.

Fig. 1.3.15

To simplify the calculations and to make available an illuminating

Minkowski diagram we shall restrict our discussion to frames of reference

whose spatial axes are in standard conﬁguration (see Figure 1.3.3)andwhose

coordinates are

therefore

related by (1.3.27)and(1.3.29). For the picture let

nsider

“r

igid” rod resting along the ˆx

-axis of

S with ends ﬁxed at

ˆx

=0andˆx

=1.Thus,thelengthoftherodasmeasuredin

S is 1. The

worldlines of the left and right ends of the rod are the ˆx

-axis and the line

ˆx

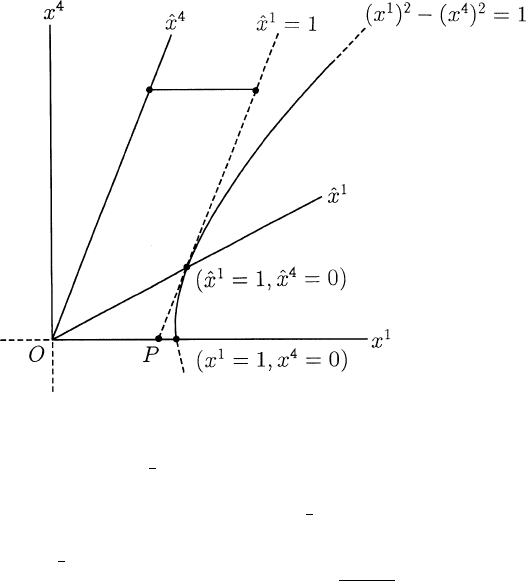
= 1 respectively. Geometrically, the measured length of the rod in S is

the Euclidean length of the segment joining two points on these worldlines at

the same instant in S (“locate the ends of the rod simultaneously and com-

pute the length from their coordinates at this instant”). Since the Euclidean

length of such a segment is clearly the same as the x

-coordinate of the point

P in Figure 1.3.16 and since this is clearly less than 1, length contraction is

visually appa

nt.

For the calculation we will be somewhat more general and consider a rod

lying along the ˆx

-axis of

S between ˆx

and ˆx

with ˆx

< ˆx

so that its

measured length in

S is Δˆx

=ˆx

−ˆx

. The worldline of the rod’s left- (resp.,

right-) hand endpoint has

S-coordinates



ˆx

, 0, 0, ˆx



(resp.,



ˆx

, 0, 0, ˆx



with −∞ < ˆx

< ∞. S will measure the length of this rod by locating

its endpoints “simultaneously”, i.e., by ﬁnding one event on each of these

worldlines with the same x

(not ˆx

). But, for any ﬁxed x

, the transformation

equations (1.3.27)give

ˆx

=(1−β

)

−

− β(1 − β

)

−

ˆx

=(1−β

)

−

− β(1 − β

)

−

1.3 The Lorentz Group 41

Fig. 1.3.16

so that Δˆx

=(1−β

)

−

Δx

and therefore

Δx

=(1−β

)

Δˆx

. (1.3.36)

Since (1 − β

)

< 1 we ﬁnd that the measured length of the rod in S is less

than its measured length in

S by a factor of



1 − β

. By reversing the roles

of S and

S we again ﬁnd that this eﬀect is entirely symmetrical.

Exercise 1.3.25 Return to Exercise 1.3.23 and oﬀer another explanation

based, not on time dilation, but on length contraction.

As it is with time dilation, the correct physical interpretation of the

Lorentz contraction often requires rather subtle and delicate argument.

Exercise 1.3.26 Imagine a barn which, at rest, measures 8 meters in length.

A (very fast) runner carries a pole of rest length 16 meters toward the barn

at such a high speed that, for an observer at rest with the barn, it appears

Lorentz contracted to 8 meters and therefore ﬁts inside the barn. This ob-

server slams the front door shut at the instant the back of the pole enters

the front of the barn and so encloses the pole entirely within the barn. But

is it not true that the runner sees the barn Lorentz contracted to 4 meters

so that the 16 meter pole could never ﬁt entirely within it? Resolve the diﬃ-

culty! Hint:LetS and

S respectively denote the rest frames of the barn and

the pole and assume that these frames are related by (1.3.27)and(1.3.29).

Calculate β. Suppose the front of the pole enters the front of the barn at

(0, 0, 0, 0). Now consider the two events at which the front of the pole hits

the back of the barn and the back of the pole enters the front of the barn.

42 1 Geometrical Structure of M

Finally, think about the maximum speed at which the signal to stop can be

communicated from the front to the back of the pole.

The underlying message of Exercise 1.3.26 would seem to be that the

classical notion of a perfectly “rigid” body has no place in relativity, even as

an idealization. The pole must compress since otherwise the signal to halt

would proceed from the front to the back instantaneously and, in particular,

the situation described in the exercise would, indeed, be “paradoxical”, i.e.,

represent a logical inconsistency.

1.4 Timelike Vectors and Curves

Let us now consider in somewhat more detail a pair of events x

and x for

which x −x

is timelike, i.e., Q(x −x

) < 0. Relative to any admissible basis

} we have (Δx

)

+(Δx

)

+(Δx

)

< (Δx

)

. Clearly then, Δx

=0

and we may assume without loss of generality that Δx

> 0, i.e., that x −x

is future-directed. Thus, we obtain

((Δx

)

+(Δx

)

+(Δx

)

Δx

< 1.

Physically, it is therefore clear that if one were to move with speed

((Δx

)

+(Δx

)

+(Δx

)

Δx

relative to the frame S corresponding to {e

} along the line in



from





to (x

) and if one were present at x

, then one would also

experience x, i.e., that there is an admissible frame of reference

S in which

and x occur at the same spatial point, one after the other. Speciﬁcally, we

now prove that if one chooses β = ((Δx

)

+(Δx

)

+(Δx

)

1/2

/Δx

and

lets d

and d

be the direction cosines in



of the directed line segment

from





to (x

), then the basis {ˆe

} for M obtained from

} by performing any Lorentz transformation whose fourth row is Λ

−β(1−β

)

−1/2

,i=1, 2, 3, and Λ

=(1−β

)

−1/2

= γ, has the property

that Δˆx

=Δˆx

=0.

Exercise 1.4.1 There will, in general, be many Lorentz transformations

with this fourth row. Show that deﬁning the remaining entries by Λ

−βγd

,i=1, 2, 3, and Λ

=(γ −1)d

+ δ

,i,j=1, 2, 3(δ

being the

Kronecker delta) gives an element of L.

To prove this we compute Δˆx

=Λ

Δx

. To simplify the calculations we

let Δ



= ((Δx

)

+(Δx

)

+(Δx

)

1/2

. We may clearly assume that Δ



=0

since otherwise there is nothing to prove. Thus, β

=Δ



/(Δx

)

,γ=

Δx



−Q(x − x

),βγ=Δ





−Q(x − x

)andd

=Δx

/Δ



for i =

1, 2, 3. From (1.3.20) we therefore obtain

1.4 Timelike Vectors and Curves 43

Δˆx

= −





−Q(x − x

)

(Δ



(Δx

)



−Q(x − x

)



−Q(x − x

Consequently, Q(x − x

)=−(Δˆx

)

. But, computing Q(x − x

)relativeto

the basis {ˆe

} we ﬁnd that Q(x −x

)=(Δˆx

)

+(Δˆx

)

+(Δˆx

)

−(Δˆx

)

so we must have (Δˆx

)

+(Δˆx

)

+(Δˆx

)

= 0, i.e., Δˆx

=Δˆx

as required.

For any timelike vector v in M we deﬁne the duration τ(v)ofv by τ(v)=



−Q(v). If v is the displacement vector v = x − x

between two events x

and x, then, as we have just shown, τ(x − x

) is to be interpreted physically

as the time separation of x

and x in any admissible frame of reference in

which both events occur at the same spatial location.

A subset of M of the form {x

+t(x−x

): t ∈ R},wherex−x

is timelike,

is called a timelike straight line in M. A timelike straight line which passes

through the origin is called a time axis. We show that the name is justiﬁed

by proving that if T is a time axis, then there exists an admissible basis {ˆe

}

for M such that the subspace of M spanned by ˆe

is T. To see this we select

an event ˜e

on T with ˜e

· ˜e

= −1 and let Span {˜e

} be the linear span of

˜e

in M. Next let Span {˜e

}

⊥

be the orthogonal complement of Span {˜e

}

in M. By Exercise 1.1.2, Span {˜e

}

⊥

is also a subspace of M. We claim that

M = Span{˜e

}⊕Span {˜e

}

⊥

(recall that a vector space V is the direct sum

of two subspaces W

and W

of V , written V = W

⊕W

,ifW

∩W

= {0}

and if every vector in V can be written as the sum of a vector in W

and a

vector in W

). Since every nonzero vector in Span {˜e

} is timelike, whereas,

by Corollary 1.3.2, every nonzero vector in Span {˜e

}

⊥

is spacelike, it is clear

that these two subspaces intersect only in the zero vector. Next we let v

denote an arbitrary vector in M and consider the vector w = v +(v · ˜e

)˜e

in M.Sincew · ˜e

= v · ˜e

+(v · ˜e

)(˜e

· ˜e

) = 0 we ﬁnd that w is in Span

{˜e

}

⊥

. Thus, the expression v = −(v · ˜e

)˜e

+ w completes the proof that

M = Span{˜e

}⊕Span{˜e

}

⊥

.Now,therestrictionoftheM-inner product

to Span {˜e

}

⊥

is positive deﬁnite so, by Theorem 1.1.1, we may select three

vectors ˜e

, ˜e

and ˜e

in Span {˜e

}

⊥

such that ˜e

· ˜e

= δ

for i, j =1, 2, 3.

Thus, {˜e

, ˜e

} is an orthonormal basis for M.Nowletusﬁxan

admissible basis {e

} for M. There is a unique orthogonal transformation

of M that carries e

onto ˜e

for each a =1, 2, 3, 4. If the corresponding

Lorentz transformation is either improper or nonorthochronous or both we

may multiply ˜e

or ˜e

or both by −1 to obtain an admissible basis {ˆe

}

for M with Span {ˆe

} = T and so the proof is complete. Any time axis is

therefore the x

-axis of some admissible coordinatization of M and so may be

identiﬁed with the worldline of some admissible observer. Since any timelike

straight line is parallel to some time axis we view such a straight line as the

worldline of a point at rest in the corresponding admissible frame (say, the

worldline of one of the “assistants” to our observer).