Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

4 Introduction

locations and times for events occurring in his immediate vicinity; the data

can later be collected for analysis by the observer.

How are the

S-coordinates of an event related to its S-coordinates?

That is, what can be said about the mapping F : R

→ R

deﬁned by

F(x

)=(ˆx

, ˆx

)? Certainly, it must be one-to-one and onto.

Indeed, F

−1

: R

→ R

must be the coordinate transformation from hat-

ted to unhatted coordinates. To say more we require a seemingly innocuous

“causality assumption.”

Any two admissible observers agree on the temporal order of any two

events on the worldline of a photon, i.e., if two such events have coor-

dinates (x

) and





in S and (ˆx

, ˆx

) and



ˆx

, ˆx



S, then x

− x

and ˆx

− ˆx

have the same sign.

Notice that we do not prejudge the issue by assuming that Δx

and Δˆx

are

equal, but only that they have the same sign, i.e., that O and

O agree as to

which of the two events occurred ﬁrst. Thus, F preserves order in the fourth

coordinate, at least for events which lie on the worldline of some photon.

How are two such events related? Since photons propagate rectilinearly with

speed 1, two events on the worldline of a photon have coordinates in S which

satisfy

− x

= v



− x



,i=1, 2, 3,

for some constants v

and v

with (v

)

+(v

)

+(v

)

=1and

consequently



− x





− x





− x



−



− x



=0. (0.1)

Geometrically, we think of (0.1) as the equation of a “cone” in R

with

vertex at





(compare (z − z

)

=(x − x

)

+(y − y

)

in R

But all of this must be true in any admissible frame of reference so F must

preserve the cone (0.1). We summarize:

The coordinate transformation map F : R

→ R

carries the cone (0.1)

onto the cone



ˆx

− ˆx





ˆx

− ˆx





ˆx

− ˆx



−



ˆx

− ˆx



=0 (0.2)

and satisﬁes ˆx

> ˆx

whenever x

and (0.1) is satisﬁed.

Being simply the coordinate transformation from hatted to unhatted co-

ordinates, F

−1

: R

→ R

has the obvious analogous properties. In 1964,

Zeeman [Z

] called such a mapping F a “causal automorphism” and proved

the remarkable fact that any causal automorphism is a composition of the

following three basic types:

1. Translations: ˆx

= x

+Λ

,a=1, 2, 3, 4, for some constants Λ

2. Positive scalar multiples: ˆx

= kx

,a=1, 2, 3, 4, for some positive

constant k.

Introduction 5

3. Linear transformations

ˆx

=Λ

,a=1, 2, 3, 4, (0.3)

where the matrix Λ = [Λ

]

a,b=1,2,3,4

satisﬁes the two conditions

ηΛ=η, (0.4)

where T means “transpose” and

η =

⎡

⎢

⎣

1000

0100

0010

000− 1

⎤

⎥

⎦

and

≥ 1. (0.5)

This result is particularly remarkable in that it is not even assumed at

the outset that F is continuous (much less, linear). We provide a proof in

Section 1.6.

Since two frames of reference related by a mapping of type 2 diﬀer only

by a trivial and unnecessary change of scale we shall banish them from fur-

ther consideration. Moreover, since the constants Λ

in maps of type 1 can

be regarded as the

S-coordinates of S’s spacetime origin we may request

that all of our observers cooperate to the extent that they select a common

event to act as origin and thereby take Λ

=0fora =1, 2, 3, 4. All that

remain for consideration then are the admissible frames of reference related

by transformations of the form (0.3) subject to (0.4) and (0.5). These are the

so-called “orthochronous Lorentz transformations” and, as we shall prove in

Chapter 1, are precisely the maps which leave invariant the quadratic form

)

+(x

)

+(x

)

− (x

)

(analogous to orthogonal transformations of

which leave invariant the usual squared length x

+ y

+ z

)andwhich

preserve “time orientation” in the sense described immediately after (0.2). It

is the geometry of this quadratic form, the structure of the group of Lorentz

transformations and their various physical interpretations that will be our

concern in the text.

With this we conclude our attempt at motivation for the deﬁnitions that

confront the reader in Chapter 1. There is, however, one more item on the

agenda of our introductory remarks. It is the cornerstone upon which the

special theory of relativity is built.

The Relativity Principle: All admissible frames of reference are com-

pletely equivalent for the formulation of the laws of physics.

The Relativity Principle is a powerful tool for building the physics of spe-

cial relativity. Since our concern is primarily with the mathematical structure

6 Introduction

of the theory we shall have few occasions to call explicitly upon the Principle

except for the physical interpretation of the mathematics and here it is vital.

We regard the Relativity Principle primarily as an heuristic principle assert-

ing that there are no “distinguished” admissible observers, i.e., that none

can claim to have a privileged view of the universe. In particular, no such

observer can claim to be “at rest” while the others are moving; they are all

simply in relative motion. We shall see that admissible observers can disagree

about some rather startling things (e.g., whether or not two given events are

“simultaneous”) and the Relativity Principle will prohibit us from preferring

the judgment of one to any of the others. Although we will not dwell on

the experimental evidence in favor of the Relativity Principle it should be

observed that its roots lie in such commonplace observations as the fact that

a passenger in a (smooth, quiet) airplane travelling at constant groundspeed

in a straight line cannot “feel” his motion relative to the earth, i.e., that no

physical eﬀects are apparent in the plane which would serve to distinguish it

from the (quasi-) admissible frame rigidly attached to the earth.

Our task then is to conduct a serious study of these “admissible frames

of reference”. Before embarking on such a study, however, it is only fair to

concede that, in fact, no such thing exists. As is the case with any intellec-

tual construct with which we attempt to model the physical universe, the

notion of an admissible frame of reference is an idealization, a rather fanciful

generalization of circumstances which, to some degree of accuracy, are en-

countered in the world. In particular, it has been found that the existence of

gravitational ﬁelds imposes severe restrictions on the “extent” (both in space

and in time) of an admissible frame. Knowing this we will intentionally avoid

the diﬃculty (until Chapter 4) by restricting our attention to situations in

which the eﬀects of gravity are “negligible.”

Chapter 1

Geometrical Structure of M

1.1 Preliminaries

We denote by V an arbitrary vector space of dimension n ≥ 1overthereal

numbers. A bilinear form on V is a map g : V×V→R that is linear

in each variable, i.e., such that g(a

+ a

,w)=a

g(v

,w)+a

g(v

,w)

and g(v, a

+ a

)=a

g(v, w

)+a

g(v, w

) whenever the a’s are real

numbers and the v’s and w’s are elements of V. g is symmetric if g(w, v)=

g(v, w) for all v and w and nondegenerate if g(v, w) = 0 for all w in V implies

v = 0. A nondegenerate, symmetric, bilinear form g is generally called an

inner product and the image of (v, w) under g is often written v ·w rather

than g(v, w). The standard example is the usual inner product on R

:ifv =

,...,v

)andw =(w

,...,w

), then g(v, w)=v ·w = v

+ ···+v

This particular inner product is positive deﬁnite, i.e., has the property that if

v =0,theng(v, v) > 0. Not all inner products share this property, however.

Exercise 1.1.1 Deﬁne a map g

: R

× R

→ R by g

(v, w)=v

+ ···+ v

n−1

−v

. Show that g

is an inner product and exhibit

nonzero vectors v and w such that g

(v, v)=0andg

(w, w) < 0.

An inner product g for which v = 0 implies g(v, v) < 0issaidtobenegative

deﬁnite,whereasifg is neither positive deﬁnite nor negative deﬁnite it is said

to be indeﬁnite.

If g is an inner product on V, then two vectors v and w for which

g(v, w)=0aresaidtobeg-orthogonal,orsimplyorthogonal if there

is no ambiguity as to which inner product is intended. If W is a sub-

space of V, then the orthogonal complement W

⊥

of W in V is deﬁned by

⊥

= {v ∈V: g(v, w) = 0 for all w ∈W}.

Exercise 1.1.2 Show that W

⊥

is a subspace of V.

The quadratic form associated with the inner product g on V is the map

Q : V→R deﬁned by Q(v)=g(v, v)=v · v (often denoted v

). We ask

, : An Introduction

, Applied Mathematical Sciences 92,

G.L. Naber The Geometry of Minkowski Spacetime to the Mathematics

of the Special Theory of Relativity

DOI 10.1007/978-1-4419-7838-7_ , © Springer Science+Business Media, LLC 2012

8 1 Geometrical Structure of M

the reader to show that distinct inner products on V cannot give rise to the

same quadratic form.

Exercise 1.1.3 Show that if g

and g

are two inner products on V which

satisfy g

(v, v)=g

(v, v) for all v in V,theng

(v, w)=g

(v, w) for all v and

w in V. Hint:Themapg

− g

: V×V→R deﬁned by (g

− g

)(v, w)=

(v, w)−g

(v, w) is bilinear and symmetric. Evaluate (g

−g

)(v +w, v+ w).

A vector v for which Q(v)iseither1or−1 is called a unit vector.Aba-

sis {e

,...,e

} for V which consists of mutually orthogonal unit vectors is

called an orthonormal basis for V and we shall now prove that such bases

always exist.

Theorem 1.1.1 Let V be an n-dimensional real vector space on which is de-

ﬁned a nondegenerate, symmetric, bilinear form g : V×V→R. Then there

exists a basis {e

,...,e

} for V such that g(e

)=0if i = j and

Q(e

)=±1 for each i =1,...,n. Moreover, the number of basis vectors

for which Q(e

)=−1 is the same for any such basis.

Proof: We begin with an observation. Since g is nondegenerate there exists

a pair of vectors (v, w)forwhichg(v, w) = 0. We claim that, in fact, there

must be a single vector u in V with Q(u) = 0. Of course, if one of Q(v)or

Q(w) is nonzero we are done. On the other hand, if Q(v)=Q(w)=0,then

Q(v +w)=Q(v)+2g(v, w)+Q(w)=2g(v, w) =0sowemaytakeu = v+w.

The proof of the theorem is by induction on n.Ifn = 1 we select any u in

V with Q(u) = 0 and deﬁne e

=(|Q(u)|)

−1/2

u.ThenQ(e

)=±1so{e

} is

the required basis.

Now we assume that n>1 and that every inner product on a vector space

of dimension less than n has a basis of the required type. Let the dimension

of V be n. Again we begin by selecting a u in V such that Q(u) =0and

letting e

=(|Q(u)|)

−1/2

u so that Q(e

)=±1. Now we let W be the orthog-

onal complement in V of the subspace Span {e

} of V spanned by {e

}.By

Exercise 1.1.2, W is

a subspace of V and

since e

is not in W,dimW <n.

The restriction of g to W×Wis an inner product on W so the induction

hypothesis assures us of the existence of a basis {e

,...,e

},m=dim W,

for W such that g(e

)=0ifi = j and Q(e

)=±1fori =1,...,m.We

claim that m = n − 1andthat{e

,...,e

} is a basis for V.

Exercise 1.1.4 Show that the vectors {e

,...,e

} are linearly

independent.

Since the number of elements in the set {e

,...,e

} is m +1≤ n,bothof

our assertions will follow if we can show that this set spans V.Thus,weletv be

an arbitrary element of V and consider the vector w = v −(Q(e

)g(v, e

))e

Then w is in W since g(w, e

)=g(v − (Q(e

)g(v, e

))e

)=g(v, e

) −

(Q(e

))

g(v, e

) = 0. Thus, we may write v = w

+ ··· + w

(Q(e

)g(v, e

))e

so {e

,...,e

} spans V.

1.2 Minkowski Spacetime 9

To show that the number r of e

for which Q(e

)=−1isthesamefor

any orthonormal basis we proceed as follows: If r = 0 the result is clear since

Q(v) ≥ 0 for every v in V, i.e., g is positive deﬁnite. If r>0, then V will

have subspaces on which g is negative deﬁnite and so will have subspaces of

maximal dimension on which g is negative deﬁnite. We will show that r is the

dimension of any such maximal subspace W and thereby give an invariant

(basis-independent) characterization of r. Number the basis elements so that

,...,e

r+1

,...,e

},whereQ(e

)=−1fori =1,...,r and Q(e

)=1

for i = r +1,...,n.LetX = Span{e

,...,e

} be the subspace of V spanned

by {e

,...,e

}. Then, since g is negative deﬁnite on X and dim X = r,we

ﬁnd that r ≤ dim W. To show that r ≥ dim W as well we deﬁne a map

T : W→Xas follows: If w =



i=1

is in W we let Tw =



i=1

Then T is obviously linear. Suppose w is such that Tw =0.Thenforeach

i =1,...,r, w

=0.Thus,

Q(w)=g

⎛

⎝



i=r+1



j=r+1

⎞

⎠



i,j=r+1

g(e



i=r+1

)

which is greater than or equal to zero. But g is negative deﬁnite on W so

we must have w

=0fori = r +1,...,n, i.e., w = 0. Thus, the null space

of T is {0} and T is therefore an isomorphism of W onto a subspace of X.

Consequently, dim W≤dim X = r as required. 

The number r of e

in any orthonormal basis for g with Q(e

)=−1 is called

the index of g. Henceforth we will assume that all orthonormal bases are

indexed in such a way that these e

appear at the end of the list and so are

numbered as follows:

,...,e

n−r

n−r+1

,...,e

}

where Q(e

)=1fori =1, 2,...,n−r and Q(e

)=−1fori = n−r+1,...,n.

Relative to such a basis if v = v

and w = w

,thenwehave

g(v, w)=v

+ ···+ v

n−r

− v

n−r+1

−···−v

1.2 Minkowski Spacetime

Minkowski spacetime is a 4-dimensional real vector space M on which is

deﬁned a nondegenerate, symmetric, bilinear form g of index 1. The elements

of M will be called events and g is referred to as a Lorentz inner product on

M. Thus, there exists a basis {e

} for M with the property that if

v = v

and w = w

,then

g(v, w)=v

+ v

− v

10 1 Geometrical Structure of M

The elements of M are “events” and, as we suggested in the Introduction,

are to be thought of intuitively as actual or physically possible point-events.

An orthonormal basis {e

} for M “coordinatizes” this event world

and is to be identiﬁed with a “frame of reference”. Thus, if x = x

+ x

, we regard the coordinates (x

)ofx relative to {e

}

as the spatial (x

)andtime(x

) coordinates supplied the event x by

the observer who presides over this reference frame. As we proceed with the

development we will have occasion to expand upon, reﬁne and add additional

elements to this basic physical interpretation, but, for the present, this will

suﬃce.

In the interest of economy we shall introduce a 4 × 4matrixη deﬁned by

η =

⎡

⎢

⎣

100 0

010 0

001 0

000−1

⎤

⎥

⎦

whose entries will be denoted either η

or η

, the choice in any particular

situation being dictated by the requirements of the summation convention.

Thus, η

= η

=1ifa = b =1, 2, 3, −1ifa = b = 4 and 0 otherwise.

As a result we may write g(e

)=η

= η

and, with the summation

convention, g(v, w)=η

Since our Lorentz inner product g on M is not positive deﬁnite there exist

nonzero vectors v in M for which g(v, v) = 0, e.g., v = e

+ e

is one such

since g(v, v)=Q(e

)+2g(e

)+Q(e

)=1+0− 1 = 0. Such vectors are

said to be null (or lightlike, for reasons which will become clear shortly) and

M actually has bases which consist exclusively of this type of vector.

Exercise 1.2.1 Construct a null basis for M, i.e., a set of four linearly

independent null vectors.

Such a null basis cannot consist of mutually orthogonal vectors, however.

Theorem 1.2.1 Two nonzero null vectors v and w in M are orthogonal if

and only if they are parallel, i.e., iﬀ there is a t in R such that v = tw.

Exercise 1.2.2 Prove Theorem 1.2.1. Hint:T

heSchwart

z Inequality for R

asserts that if x =(x

)andy =(y

), then

+ x

)

≤ ((x

)

+(x

)

+(x

)

)((y

)

+(y

)

+(y

)

and that equality holds if and only if x and y are linearly dependent. 

Next consider two distinct events x

and x for which the displacement vector

v = x − x

from x

to x is null, i.e., Q(v)=Q(x − x

) = 0. Relative to any

orthonormal basis {e

},ifx = x

and x

= x

,then



− x





− x





− x



−



− x



=0. (1.2.1)

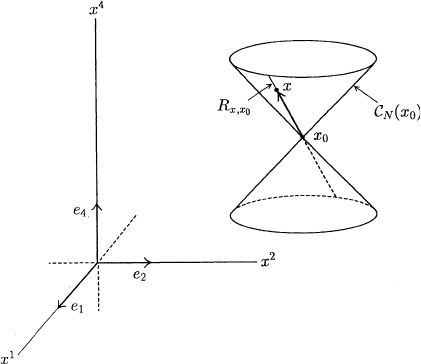
1.2 Minkowski Spacetime 11

Fig. 1.2.1

But we have seen this before. It is precisely the condition which, in the

Introduction, we decided describes the relationship between two events that

lie on the worldline of some photon. For this reason, and because of the formal

similarity between (1.2.1) and the equation of a right circular cone in R

,we

deﬁne the null cone (or light cone) C

) at x

in M by

)={x ∈M: Q(x − x

)=0}

and picture it by suppressing the third spatial dimension x

(see Figure 1.2.1).

) therefore consists of all those events in M that are “connectible to

by a light ray”. For any such event x (other than x

itself) we deﬁne the

null worldline (or light ray) R

containing x

and x by

= {x

+ t(x − x

):t ∈ R}

and think of it as the worldline of that particular photon which experiences

both x

and x.

Exercise 1.2.3 Show that if Q(x − x

)=0,thenR

x,x

= R

) is just the union of all the light rays through x

. Indeed,

Theorem 1.2.2 Let x

and x be two distinct events with Q(x−x

)=0.Then

= C

) ∩C

(x). (1.2.2)

Proof: First let z = x

+ t(x − x

)beanelementofR

.Thenz −x

t(x−x

)soQ(z−x

)=t

Q(x−x

)=0soz is in C

). With Exercise 1.2.3

it follows in the same way that z is in C

(x)andsoR

⊆C

) ∩C

(x).

12 1 Geometrical Structure of M

To prove the reverse containment we assume that z is in C

) ∩C

(x).

Then each of the vectors z − x, z − x

and x

− x is null. But z − x

(z−x)−(x

−x)so0=Q(z−x

)=Q(z−x) −2g(z−x, x

−x)+Q(x

−x)=

−2g(z −x, x

−x). Thus, g(z −x, x

−x)=0.Ifz = x we are done. If z = x,

then, since x = x

, we may apply Theorem 1.2.1 to the orthogonal null

vectors z − x and x

− x to obtain a t in R such that z − x = t(x

− x)and

it follows that z is in R

as required. 

For reasons which may not be apparent at the moment, but will become

clear shortly, a vector v in M is said to be timelike if Q(v) < 0andspacelike

if Q(v) > 0.

Exercise 1.2.4 Use an orthonormal basis for M to construct a few vectors

of each type.

If v is the displacement vector x − x

between two events, then, relative to

any orthonormal basis for M, Q(x − x

) < 0 becomes (Δx

)

+(Δx

)

(Δx

)

< (Δx

)

(x − x

is inside thenullconeatx

). Thus, the (squared)

spatial separation of the two events is less than the (squared) distance light

would travel during the time lapse between the events (remember that x

measured in light travel time). If x−x

is spacelike the inequality is reversed,

we picture x −x

outside the null cone at x

and the spatial separation of x

and x is so great that not even a photon travels quickly enough to experience

both events.

If {e

} and {ˆe

, ˆe

} are two orthonormal bases for M,then

there is a unique linear transformation L : M→Msuch that L(e

)=ˆe

for

each a =1, 2, 3, 4. As we shall see, such a map “preserves the inner product

of M”, i.e., is of the following type: A linear transformation L : M→Mis

said to be an orthogonal transformation of M if g(Lx , Ly)=g(x, y) for all x

and y in M.

Exercise 1.2.5 Show that, since the inner product on M is nondegener-

ate, an orthogonal transformation is necessarily one-to-one and therefore an

isomorphism.

Lemma 1.2.3 Let L : M→Mbe a linear transformation. Then the fol-

lowing are equivalent:

(a) L is an orthogonal transformation.

(b) L preserves the quadratic form of M, i.e., Q(Lx )=Q(x) for all x in M.

for M.

Exercise 1.2.6 Prove Lemma 1.2.3. Hi

nt:

To prove that (b) implies (a)

compute L(x + y) · L(x + y) − L(x − y) · L(x − y). 

w let L : M→M be an orthogonal transformation of M and

} an orthonormal basis for M. By Lemma 1.2.3,ˆe

= Le

, ˆe

= Le

and ˆe

= Le

also form an orthonormal basis for M.In

1.2 Minkowski Spacetime 13

particular, each e

,u=1, 2, 3, 4, can be expressed as a linear combination

of the ˆe

=Λ

ˆe

+Λ

ˆe

+Λ

ˆe

+Λ

ˆe

=Λ

ˆe

,u=1, 2, 3, 4, (1.2.3)

where the Λ

are constants. Now, the orthogonality conditions g(e

)=η

c, d =1, 2, 3, 4, can be written

+Λ

− Λ

= η

(1.2.4)

or, with the summation convention,

= η

,c,d=1, 2, 3, 4. (1.2.5)

Exercise 1.2.7 Show that (1.2.5)isequivalentto

= η

,a,b=1, 2, 3, 4. (1.2.6)

We deﬁne the matrix Λ=[Λ

]

a,b=1,2,3,4

associated with the orthogonal

transformation L and the orthonormal basis {e

} by

Λ=

⎡

⎢

⎣

⎤

⎥

⎦

Observe that Λ is actually the matrix of L

−1

relative to the basis {ˆe

Heuristically, conditions (1.2.5) assert that “the columns of Λ are mutually

orth

ogonal

unit vectors”, whereas (1.2.6) makes the same statement about

the

ows.

e regard the matrix Λ associated with L and {e

} as a coordinate trans-

formation matrix in the usual way. Speciﬁcally, if the event x in M has co-

ordinates x = x

+ x

relative to {e

}, then its coordinates

relative to {ˆe

} = {Le

} are x =ˆx

ˆe

+ˆx

ˆe

+ˆx

ˆe

+ˆx

ˆe

,where

ˆx

=Λ

+Λ

ˆx

=Λ

+Λ

ˆx

=Λ

+Λ

ˆx

=Λ

+Λ

which we generally write more concisely as

ˆx

=Λ

,a=1, 2, 3.4. (1.2.7)

Exercise 1.2.8 By performing the indicated matrix multiplications show

that (1.2.5) [and therefore (1.2.6)] is equivalent to

ηΛ=η, (1.2.8)

where T means “transpose”.