Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

14 1 Geometrical Structure of M

Notice that we have seen (1.2.8) before. It is just equation (0.4)ofthe

Introduction, which perhaps seems somewhat less mysterious now than it

did then. Indeed, (1.2.8) is now seen to be the condition that Λ is the

trix o

f a linear transformation which preserves the quadratic form of

M. In particular, if x − x

is the displacement vector between two events

for which Q(x − x

) = 0, then both (Δx

)

+(Δx

)

+(Δx

)

− (Δx

)

and (Δˆx

)

+(Δˆx

)

+(Δˆx

)

− (Δˆx

)

,wheretheΔˆx

are, from (1.2.7),

Δˆx

=Λ

Δx

, are zero. Physically, the two observers presiding over the

hatted and unhatted reference frames agree that x

and x are “connectible

by a light ray”, i.e., they agree on the speed of light.

Any 4 ×4 matrix Λ that satisﬁes (1.2.8) is called a gen

eral (homo

geneous)

Lorentz transformation. At times we shall indulge in a traditional abuse of

terminology and refer to the coordinate transformation (1.2.7)asaLorentz

ansf

ormation. Since the orthogonal transformations of M are isomorphisms

and therefore invertible, the matrix Λ associated with such an orthogonal

transformation must be invertible [also see (1.3.6)]. From (1.2.8) we ﬁnd that

ηΛ=η implies Λ

η = ηΛ

−1

so that Λ

−1

= η

−1

η or, since η

−1

= η,

−1

= ηΛ

η. (1.2.9)

Exercise 1.2.9 Show that the set of all general (homogeneous) Lorentz

transformations forms a group under matrix multiplication, i.e., that it is

closed under the formation of products and inverses. This group is called the

general (homogeneous) Lorentz group and we shall denote it by L

We shall denote the entries in the matrix Λ

−1

by Λ

so that, by (1.2.9),

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

−Λ

⎤

⎥

⎦

. (1.2.10)

Exercise 1.2.10 Show that

= η

,a,b=1, 2, 3, 4, (1.2.11)

and similarly

= η

,a,b=1, 2, 3, 4. (1.2.12)

Since we have seen (Exercise 1.2.9)thatΛ

−1

is in L

whenever Λ is it must

also satisfy conditions analogous to (1.2.5)and(1.2.6), namely,

= η

,c,d=1, 2, 3, 4, (1.2.13)

and

= η

,a,b=1, 2, 3, 4. (1.2.14)

1.3 The Lorentz Group 15

The analogues of (1.2.3)and(1.2.7)are

ˆe

=Λ

,u=1, 2, 3, 4, (1.2.15)

and

=Λ

ˆx

,b=1, 2, 3, 4. (1.2.16)

1.3 The Lorentz Group

Observe that by setting c = d =4in(1.2.5)oneobtains





=1+













so that, in particular,





≥ 1. Consequently,

≥ 1orΛ

≤−1 (1.3.1)

An element Λ of L

is said to be orthochronous if Λ

≥1and

nonorthochronous if Λ

≤−1. Nonorthochronous Lorentz transforma-

tions have certain unsavory characteristics which we now wish to expose.

First, however, the following extremely important preliminary.

Theorem 1.3.1 Suppose that v is timelike and w is either timelike or null

and nonzero. Let {e

} be an orthonormal basis for M with v = v

and

w = w

. Then either

(a) v

> 0,inwhichcaseg(v, w) < 0,or

(b) v

< 0,inwhichcaseg(v, w) > 0.

Proof: By assumption we have g(v, v)=(v

)

+(v

)

+(v

)

− (v

)

< 0

and (w

)

+(w

)

+(w

)

−(w

)

≤ 0so(v

)

> ((v

)

+(v

)

)((w

)

+(w

)

+(w

)

) ≥ (v

)

, the second inequality

following from the Schwartz Inequality for R

(see Exercise 1.2.2). Thus, we

ﬁnd that



+ v



so, in particular, v

= 0 and, moreover, g(v, w) = 0. Suppose that

> 0. Then v

= |v

| > |v

|≥v

and so v

+ v

−v

< 0, i.e., g(v, w) < 0. On the other hand,

if v

< 0, then g(v, −w) < 0sog(v, w) > 0. 

Corollary 1.3.2 If a nonzero vector in M is orthogonal to a timelike vector,

then it must be spacelike.

We denote by τ the collection of all timelike vectors in M and deﬁne a

relation ∼ on τ as follows: If v and w are in τ,thenv ∼ w if and only if

g(v, w) < 0(sothatv

and w

have the same sign in any orthonormal basis).

16 1 Geometrical Structure of M

Exercise 1.3.1 Verify that ∼ is an equivalence relation on τ with precisely

two equivalence classes. That is, show that ∼ is

1. reﬂexive (v ∼ v for every v in τ ),

2. symmetric (v ∼ w implies w ∼ v),

3. transitive (v ∼ w and w ∼ x imply v ∼ x)

and that τ is the union of two disjoint subsets τ

and τ

−

with the property

that v ∼ w for all v and w in τ

,v∼ w for all v and w in τ

−

and v/∼ w if

one of v or w is in τ

and the other is in τ

−

Fig. 1.3.1

We think of the elements of τ

(and τ

−

) as having the same time orientation.

More speciﬁcally, we select (arbitrarily) τ

and refer to its elements as future-

directed timelike vectors, whereas the vectors in τ

−

we call past-directed.

Exercise 1.3.2 Show that τ

(and τ

−

)arecones, i.e., that if v and w are

in τ

(τ

−

)andr is a positive real number, then rv and v + w are also in

(τ

−

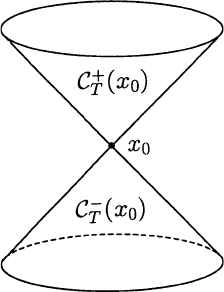
For each x

in M we deﬁne the time cone C

), future time cone C

)

and past time cone C

−

) at x

)={x ∈M: Q(x − x

) < 0},



x ∈M: x − x

∈ τ



= C

) ∩ τ

and

−



x ∈M: x − x

∈ τ

−



= C

) ∩ τ

−

We picture C

) as the interior of the null cone C

). It is the disjoint

union of C

)andC

−

) and we shall adopt the convention that our

pictures will always be drawn with future-directed vectors “pointing up” (see

Figure 1.3.1).

1.3 The Lorentz Group 17

We wish to extend the notion of past- and future-directed to nonzero null

vectors as well. First we observe that if n is a nonzero null vector, then

n · v has the same sign for all v in τ

. To see this we suppose that there

exist vectors v

and v

in τ

such that n · v

< 0andn · v

> 0. We may

assume that |n · v

| = n · v

since if this is not the case we can replace

by (n · v

/|n · v

|)v

, which is still in τ

by Exercise 1.3.2 and satisﬁes

g(n, (n·v

/|n·v

|)v

)=(n·v

/|n·v

|)g(n, v

)=−n·v

.Thus,n·v

= −n·v

so n·v

+n·v

= 0 and therefore n·(v

) = 0. But, again by Exercise 1.3.2,

+ v

is in τ

and so, in particular, is timelike. Since n is nonzero and null

this contradicts Corollary 1.3.2. Thus, we may say that a nonzero null vector

n is fu

ure

-directed if n ·v<0 for all v in τ

and past-directed if n ·v>0for

all v in τ

Exercise 1.3.3 Show that two nonzero null vectors n

and n

have the same

time orientation (i.e., are both past-directed or both future-directed) if and

only if n

and n

have the same sign relative to any orthonormal basis for M.

For any x

in M we deﬁne the future null cone at x

by C

{x ∈C

):x − x

is future-directed} and the past null cone at x

−

)={x ∈C

):x − x

is past-directed}. Physically, event x is in

)ifx

and x respectively can be regarded as the emission and recep-

tion of a light signal. Consequently, C

) may be thought of as the history

in spacetime of a spherical electromagnetic wave (photons in all directions)

whose emission event is x

(see Figure 1.3.2).

The disagreeable nature of nonorthochronous Lorentz transformations is

that they always reverse time orientations (and so presumably relate reference

frames in which someone’s clock is running backwards).

Theorem 1.3.3 Let Λ= [Λ

]

a,b=1,2,3,4

be an element of L

and

}

a=1,2,3,4

an orthonormal basis for M. Then the following are equivalent:

(a) Λ is orthochronous.

(b) Λ preserves the time orientation of all nonzero null vectors, i.e., if v =

is a nonzero null vector, then the numbers v

and ˆv

=Λ

have

the same sign.

Proof: Let v = v

be a vector which is either timelike or null and nonzero.

By the Schwartz Inequality for R

we have



+Λ



≤





i=1









i=1







. (1.3.2)

Now, by (1.2.6)witha = b =4,w

ave













−





= −1 (1.3.3)

18 1 Geometrical Structure of M

Fig. 1.3.2

and so

















.Moreover,sincev is either timelike

or null, (v

)

≥ (v

)

+(v

)

+(v

)

.Sincev is nonzero, (1.3.2) therefore

yields



+Λ







,whichwemaywriteas



+Λ

− Λ



+Λ



< 0.

(1.3.4)

Deﬁne w in M by w =Λ

+Λ

.By(1.3.3), w is

timelike. Moreover, (1.3.4) can now be written

(v · w)ˆv

< 0. (1.3.5)

Consequently, v · w and ˆv

have opposite signs.

We now show that Λ

≥ 1 if and only if v

and ˆv

have the same sign.

First suppose Λ

≥ 1. If v

> 0, then, by Theorem 1.3.1, v ·w<0soˆv

> 0

by (1.3.5). Similarly, if v

< 0, then v ·w>0soˆv

< 0. Thus, Λ

≥ 1 implies

that v

and ˆv

havethesamesign.Inthesameway,Λ

≤−1 implies that

and ˆv

have opposite signs. 

Notice that we have actually shown that if Λ is nonorthochronous, then it

necessarily reverses the time orientation of all timelike and nonzero null vec-

tors. For this reason we elect to restrict our attention henceforth to the or-

thochronous elements of L

. Since such a Lorentz transformation never

reverses the time orientation of a timelike vector we may also limit ourselves

to orthonormal bases {e

} with e

future-directed. At this point

the reader may wish to return to the Introduction with a somewhat better

understanding of why the condition Λ

≥ 1 appeared in Zeeman’s Theorem.

1.3 The Lorentz Group 19

Thereisyetonemorerestrictionwewouldliketoimposeonour

Lorentz transformations. Observe that taking determinants on both sides

of (1.2.8) yields (det Λ

)(det η)(det Λ) = det η so that, since det Λ

det Λ, (det Λ)

= 1 and therefore

det Λ = 1 or det Λ = −1. (1.3.6)

We shall say that a Lorentz transformation Λ is proper if det Λ = 1 and

improper if det Λ = −1.

Exercise 1.3.4 Show that an orthochronous Lorentz transformation is im-

proper if and only if it is of the form

⎡

⎢

⎣

−1 000

0100

0010

0001

⎤

⎥

⎦

Λ, (1.3.7)

where Λ is proper and orthochronous.

Notice that the matrix on the left in (1.3.7) is an orthochronous Lorentz

ansf

ormation and, as a coordinate transformation, has the eﬀect of chang-

ing the sign of the ﬁrst spatial coordinate, i.e., of reversing the spatial orienta-

tion (left-handed to right-handed or right-handed to left-handed). Since there

seems to be no compelling reason to make such a change we intend to restrict

our attention to the set L of proper, orthochronous Lorentz transformations.

Having done so we may further limit the orthonormal bases we consider by

selecting an orientation for the spatial coordinate axes. Speciﬁcally, we de-

ﬁne an admissible basis for M to be an orthonormal basis {e

}

with e

timelike and future-directed and {e

} spacelike and “right-

handed”, i.e., satisfying e

× e

· e

= 1 (since the restriction of g to the

span of {e

} is the usual dot product on R

, the cross product and dot

product here are the familiar ones from vector calculus). At this point we

fully identify an “admissible basis” with an “admissible frame of reference”

as discussed in the Introduction. Any two such bases (frames) are related by

a proper, orthochronous Lorentz transformation.

Exercise 1.3.5 Show that the set L of proper, orthochronous Lorentz trans-

formations is a subgroup of L

, i.e., that it is closed under the formation

of products and inverses.

Generally, we shall refer to L simply as the Lorentz group and its elements

as Lorentz transformations with the understanding that they are all proper

and orthochronous. Occasionally it is convenient to enlarge the group of coor-

dinate transformations to include spacetime translations (see the statement

of Zeeman’s Theorem in the Introduction), thereby obtaining the so-called

inhomogeneous Lorentz group or Poincar´egroup. Physically, this amounts to

allowing “admissible” observers to use diﬀerent spacetime origins.

20 1 Geometrical Structure of M

The Lorentz group L has an important subgroup R consisting of those

R =[R

]oftheform

R =

⎡

⎢

⎣





0001

⎤

⎥

⎦

where [R

]

i,j=1,2,3

is a unimodular orthogonal matrix, i.e., satisﬁes

det[R

]=1and[R

]

=[R

]

−1

. Observe that the orthogonality con-

ditions (1.2.5) are clearly satisﬁed by such an R and

at, moreover, R

and det R =det[R

]=1sothatR is indeed in L. The coordinate transfor-

mation associated with R corresponds physically to a rotation of the spatial

coordinate axes within a given frame of reference. For this reason R is called

the rotation subgroup of L and its elements are called rotations in L.

Lemma 1.3.4 Let Λ=[Λ

]

a,b=1,2,3,4

be a proper, orthochronous Lorentz

transformation. Then the following are equivalent:

(a) Λ is a rotation,

(b) Λ

=Λ

=0,

=Λ

=0,

(d) Λ

=1.

Proof: Set c = d =4in(1.2.5)toobtain













−





= −1. (1.3.8)

Similarly, with a = b =4,(1.2.6) becomes













−





= −1. (1.3.9)

The equivalence of (b), (c) and (d) now follows immediately from (1.3.8)and

(1.3.9) and the fact that Λ is assumed orthochronous. Since a rotation in L

tisﬁes

(b), (c)

and (d) by deﬁnition, all that remains is to show that if Λ

satisﬁes one (and therefore all) of these conditions, then





i,j=1,2,3

is a

unimodular orthogonal matrix.

Exercise 1.3.6 Complete the proof. 

Exercise 1.3.7 Use Lemma 1.3.4 to show that R is a

subg

roup of L, i.e.,

that it is closed under the formation of inverses and products.

Exercise 1.3.8 Show that an element of L has the same fourth row as

[Λ

]

a,b=1,2,3,4

if and only if it can be obtained from [Λ

] by multiplying on

the left by some rotation in L. Similarly, an element of L has the same fourth

column as [Λ

] if and only if it can be obtained from [Λ

] by multiplying

on the right by an element of R.

1.3 The Lorentz Group 21

There are 16 parameters in every Lorentz transformation, although, by

virtue of the relations (1.2.5), these are not all independent. We now derive

mple ph

ysical interpretations for some of these parameters. Thus, we con-

sider two admissible bases {e

} and {ˆe

} and the corresponding admissible

frames of reference S and

S. Any two events on the worldline of a point

which can be interpreted physically as being at rest in

S have coordinates in

S which satisfy Δˆx

=Δˆx

=0andΔˆx

= the time separation of the

two events as measured in

S.From(1.2.16) we ﬁnd that the corresponding

rdina

te diﬀerences in S are

Δx

=Λ

Δˆx

=Λ

Δˆx

. (1.3.10)

From (1.3.10) and the fact that Λ

and Λ

are nonzero it follows that the

ratios

Δx

= −

,i=1, 2, 3,

are constant and independent of the particular point at rest in

S we choose

to examine. Physically, these ratios are interpreted as the components of the

ordinary velocity 3-vector of

S relative to S:



= u

+ u

, where u

= −

,i=1, 2, 3 (1.3.11)

(notice that we use the term “3-vector” and the familiar vector notation

to distinguish such highly observer-dependent spatial vectors whose physical

interpretations are not invariant under Lorentz transformations, but which

are familiar from physics). Similarly, the velocity 3-vector of S relative to

S is



ˆu =ˆu

ˆe

+ˆu

ˆe

+ˆu

ˆe

, where ˆu

−

,i=1, 2, 3. (1.3.12)

Next observe that



i=1

(Δx

/Δx

)

=(Λ

)

−2



i=1

(Λ

)

=(Λ

)

−2

[(Λ

)

− 1]. Similarly,



i=1

(Δˆx

/Δˆx

)

=(Λ

)

−2

[(Λ

)

− 1]. Physically,

we interpret these equalities as asserting that the velocity of

S relative to S

and the velocity of S relative to

S have the same constant magnitude which

we shall denote by β.Thus,β

=1− (Λ

)

−2

, so, in particular, 0 ≤ β

< 1

and β = 0 if and only if Λ is a rotation (Lemma 1.3.4). Solving for Λ

(and

taking the positive square root since Λ is assumed orthochronous) yields

=(1−β

)

−

(= Λ

). (1.3.13)

The quantity (1 − β

)

−1/2

will occur frequently and is often designated γ.

Assuming that Λ is not a rotation we may write



= β



= β(d

+ d

),d

= u

/β, (1.3.14)

22 1 Geometrical Structure of M

where



is the direction 3-vector of

S relative to S and the d

are interpreted

as the direction cosines of the directed line segment in



along which the

observer in S sees



moving. Similarly,



ˆu = β



d = β(

ˆe

=ˆu

/β. (1.3.15)

Exercise 1.3.9 Show that the d

are the components of the normalized

projection of ˆe

onto the subspace spanned by {e

}, i.e., that

⎛

⎝



j=1

(ˆe

· e

)

⎞

⎠

−

(ˆe

· e

),i=1, 2, 3, (1.3.16)

and similarly

⎛

⎝



j=1

· ˆe

)

⎞

⎠

−

· ˆe

),i=1, 2, 3. (1.3.17)

Exercise 1.3.10 Show that ˆe

= γ(β



) and, similarly, e

= γ(β



d +ˆe

)

and notice that it follows from these that e

· ˆe

=ˆe

· e

= −γ.

Comparing (1.3.11)and(1.3.14) and using (1.3.13)weobtain

= −Λ

= β(1 − β

)

−

,i=1, 2, 3, (1.3.18)

and similarly

= −Λ

= β(1 − β

)

−

,i=1, 2, 3. (1.3.19)

Equations (1.3.13), (1.3.18)and(1.3.19) give the last row and column of Λ

in t

erm

s of physically measurable quantities and even at this stage a number

of interesting kinematic consequences become apparent. Indeed, from (1.2.7)

ain

Δˆx

= −βγ



Δx

+ d

Δx

+ d

Δx



+ γΔx

(1.3.20)

for any two events. Let us consider the special case of two events on the

worldline of a point at rest in S.ThenΔx

=Δx

=0so(1.3.20)

becomes

Δˆx

= γΔx



1 − β

Δx

. (1.3.21)

In particular, Δˆx

=Δx

if and only if Λ is a rotation. Any relative motion

of S and

S gives rise to a time dilation eﬀect according to which Δˆx

> Δx

Since our two events can be interpreted as two readings on one of the clocks

at rest in S,anobserverin

S will conclude that the clocks in S are running

slow (even though they are, by assumption, identical).

1.3 The Lorentz Group 23

Exercise 1.3.11 Show that this time dilation eﬀect is entirely symmetrical,

i.e., that for two events with Δˆx

=Δˆx

=0,

Δx

= γΔˆx



1 − β

Δˆx

. (1.3.22)

We shall return to this phenomenon of time dilation in much greater detail

after we have introduced a geometrical construction for picturing it. Never-

theless, we should point out at the outset that it is in no sense an illusion;

it is quite “real” and can manifest itself in observable phenomena. One such

instance occurs in the study of cosmic rays (“showers” of various types of

elementary particles from space which impact the earth). Certain types of

mesons that are encountered in cosmic radiation are so short-lived (at rest)

that even if they could travel at the speed of light (which they cannot) the

time required to traverse our atmosphere would be some ten times their nor-

mal life span. They should not be able to reach the earth, but they do. Time

dilation, in a sense, “keeps them young”. The meson’s notion of time is not

the same as ours. What seems a normal lifetime to the meson appears much

longer to us. It is well to keep in mind also that we have been rather vague

about what we mean by a “clock”. Essentially any phenomenon involving ob-

servable change (successive readings on a Timex, vibrations of an atom, the

lifetime of a meson, or a human being) is a “clock” and is therefore subject

to the eﬀects of time dilation. Of course, the eﬀects will be negligibly small

unless β is quite close to 1 (the speed of light). On the other hand, as β → 1,

(1.3.21)showsthatΔˆx

→∞so that as speeds approach that of light the

eﬀects become inﬁnitely great.

Another special case of (1.3.20) is also of interest. Let us suppose that our

wo e

vents are judged simultaneous in S, i.e., that Δx

=0.Then

Δˆx

= −βγ



Δx

+ d

Δx

+ d

Δx



. (1.3.23)

Again assuming that β = 0 we ﬁnd that, in general, Δˆx

will not be zero,

i.e., that the two events will not be judged simultaneous in

S. Indeed, S and

S will agree on the simultaneity of these two events if and only if the spatial

locations of the events in



bear a very special relation to the direction in



along which



is moving, namely,

Δx

+ d

Δx

+ d

Δx

= 0 (1.3.24)

(the displacement vector in



between the locations of the two events is

either zero or nonzero and perpendicular to the direction of



’s motion in



). Otherwise, Δˆx

= 0 and we have an instance of what is called the

relativity of simultaneity. Notice, incidentally, that such disagreement can

arise only for spatially separated events. More precisely, if in some admissible

frame S two events x and x

are simultaneous and occur at the same spatial

location, then Δx

=0fora =1, 2, 3, 4sox − x

= 0. Since the Lorentz

transformations are linear it follows that Δˆx

=0fora =1, 2, 3, 4, i.e., the

events are also simultaneous and occur at the same spatial location in

Again, we will return to this phenomenon in much greater detail shortly.