Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

54 1 Geometrical Structure of M

The general solution to (1.4.21) can be written

= U

(τ)=a sinh gτ + b cosh gτ.

Assuming that the explorer accelerates from rest at τ =0(U

(0) = 0,

(0) = g)oneobtains

(τ)=sinhgτ. (1.4.22)

Equation (1.4.19)nowgives

(τ)=coshgτ. (1.4.23)

Integrating (1.4.22)and(1.4.23) and assuming, for convenience, that x

(0) =

1/g and x

(0) = 0, one obtains

⎧

⎪

⎨

⎪

⎩

cosh gτ,

sinh gτ.

(1.4.24)

Observe that (1.4.24) implies that (x

)

−(x

)

=1/g

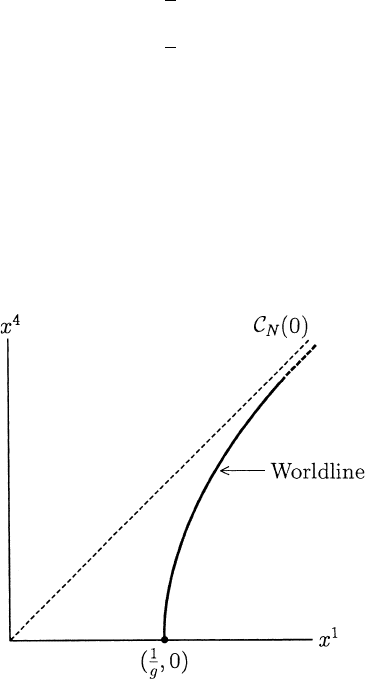
so that our explorer’s

worldline lies on a hyperbola in the 2-dimensional representation of M (see

Figure 1.4.1).

Exercise 1.4.15 Assume that the explorer’s point of departure (at x

1/g) was the earth, which is at rest in the frame of reference under consid-

eration. How far from the earth (as measured in the earth’s frame) will the

explorer be after

Fig. 1.4.1

1.5 Spacelike Vectors 55

(a) 40 years as measured on earth? (How much time will have elapsed on the

rocket?) Answers: 39 light years (4.38 years).

(b) 40 years as measured on the rocket? (How much time will have elapsed

on earth?) Answers:10

light years (10

years).

Hint: It will simplify the arithmetic to measure in light years rather than

meters. Then g ≈ 1 (light year)

−1

We conclude this section with a theorem which asserts quite generally

that an accelerated observer such as the explorer in the preceding discussion

of hyperbolic motion or the “rocket twin” in the twin paradox must always

experience a time dilation not experienced by those of us who remain at rest

in an admissible frame.

Theorem 1.4.8 Let α :[a, b] →Mbe a timelike worldline in M from

α(a)=q to α(b)=p.Then

L(α) ≤ τ(p − q) (1.4.25)

and equality holds if and only if α is a parametrization of a timelike straight

line joining q and p.

Proof: By Theorem 1.4.6, p − q is timelike and future-directed so we may

select a basis {e

} with q = x

+ x

,p= x

+ x

and τ(p − q)=x

−x

=Δx

.Nowparametrizeα by x

.Then

L(α)=



1 −













≤



=Δx

= τ(p − q).

Moreover, equality holds if and only if

=0fori =1, 2, 3, that is, if

and only if x

is constant for i =1, 2, 3 and this is the case if and only if

α(x

)=x

+ x

for x

≤ x

as required. 

1.5 Spacelike Vectors

Now we turn to spacelike separations, i.e., we consider two events x and x

for which Q(x − x

) > 0. Relative to any admissible basis we have (Δx

)

(Δx

)

+(Δx

)

> (Δx

)

so that x −x

lies outside thenullconeatx

and

there is obviously no admissible basis in which the spatial separation of the

two events is zero, i.e., there is no admissible observer who can experience

both events (to do so he would have to travel faster than the speed of light).

However, an argument analogous to that given at the beginning of Section 1.4

will show that there is a frame in which x and x

are simultaneous.

56 1 Geometrical Structure of M

Exercise 1.5.1 Show that if Q(x − x

) > 0, then there is an admissible

basis {ˆe

} for M relative to which Δˆx

=0.Hint:With{e

} arbitrary, take

β =

Δx



and d

Δx



and proceed as at the beginning of Section 1.4.

Exercise 1.5.2 Show that if Q(x−x

) > 0ands is an arbitrary real number

(positive, negative or zero), then there is an admissible basis for M relative

to which the temporal separation Δx

of x and x

is s (so that admissible

observers will, in general, not even agree on the temporal order of x and x

Since ((Δx

)

+(Δx

)

+(Δx

)



(Δx

)

+ Q(x − x

)inanyadmis-

sible frame and since (Δx

)

can assume any non-negative real value, the

spatial separation of x and x

can assume any value greater than or equal



Q(x − x

); there is no frame in which the spatial separation is less than

this value. For any two events x and x

for which Q(x − x

) > 0 we deﬁne

the proper spatial separation S(x − x

)ofx and x

S(x − x



Q(x − x

and regard it as the spatial separation of x and x

in any frame of reference

in which x and x

are simultaneous.

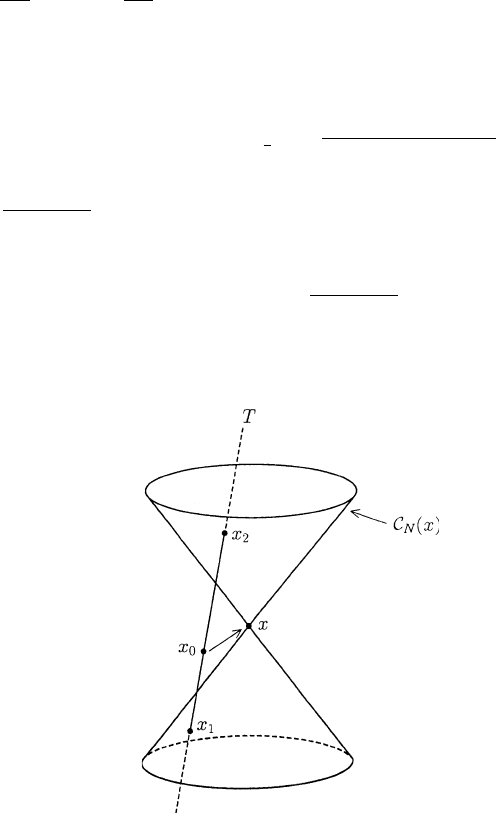
Fig. 1.5.1

Let T be an arbitrary timelike straight line containing x

. We have seen

that T can be identiﬁed with the worldline of some observer at rest in an

admissible frame, but not necessarily stationed at the origin of the spatial

coordinate system of this frame (we consider the special case of a time axis

shortly). Let x in M be such that x −x

is spacelike and let x

and x

be the

points of intersection of T with C

(x)asshowninFigure1.5.1. We claim that

(x − x

)=τ(x

− x

)τ(x

− x

) (1.5.1)

1.5 Spacelike Vectors 57

(a result ﬁrst proved by Robb [R]). To prove (1.5.1) we observe that, since

x − x

is null,

0=Q(x − x

)=Q((x

− x

)+(x − x

)),

0=−τ

− x

)+2(x

− x

) ·(x − x

)+S

(x − x

). (1.5.2)

Similarly, since x

− x is null,

0=−τ

− x

) − 2(x

− x

) ·(x − x

)+S

(x − x

). (1.5.3)

There exists a constant k>0 such that x

− x

= k(x

− x

)soτ

−

)=k

−x

). Multiplying (1.5.2)byk and adding the result to (1.5.3)

therefore yields

−(k + k

)τ

− x

)+(k +1)S

(x − x

)=0.

Since k +1= 0 this can be written

(x − x

)=kτ

− x

)

= τ(x

− x

)(kτ(x

− x

))

= τ(x

− x

)τ(x

− x

)

as required.

Suppose that the spacelike displacement vector x −x

is orthogonal to the

timelike straight line T . Then (with the notation as above) (x

−x

)·(x−x

−x

) ·(x −x

)=0so(1.5.2)and(1.5.3) yield S(x −x

)=τ(x

−x

τ(x

− x

) which we prefer to write as

S(x − x

(τ(x

− x

)+τ(x

− x

)). (1.5.4)

In particular, this is true if T is a time axis. We have seen that, in this

case, T can be identiﬁed with the worldline of an admissible observer O and

the events x and x

are simultaneous in this observer’s reference frame. But

then S(x − x

) is the distance in this frame between x and x

.Sincex

lies on T we ﬁnd that (1.5.4) admits the following physical interpretation:

The O-distance of an event x from an admissible observer O is one-half the

time lapse measured by O between the emission and reception of light signals

connecting O with x.

Exercise 1.5.3 Let x, x

and x

be events for which x −x

and x

−x are

spacelike and orthogonal. Show that

− x

)=S

− x)+S

(x − x

) (1.5.5)

and interpret the result physically by considering a time axis T which is

orthogonal to both x − x

and x

− x.

58 1 Geometrical Structure of M

Suppose that v and w are nonzero vectors in M with v · w =0.Thus

farwehaveshownthefollowing:Ifv and w are null, then they must

be parallel (Theorem 1.2.1). If v is timelike, then w must be spacelike

(Corollary 1.3.2). If v and w are spacelike, then their proper spatial lengths

satisfy the Pythagorean Theorem S

(v+w)=S

(v)+S

(w) (Exercise 1.5.3).

Exercise 1.5.4 Can a spacelike vector be orthogonal to a nonzero null

vector?

1.6 Causality Relations

We begin by deﬁning two order relations  and < on M as follows: For x

and y in M we say that x chronologically precedes y and write x  y if

y −x is timelike and future-directed, i.e., if y is in C

(x). We will say that x

causally precedes y and write x<yif y − x is null and future-directed, i.e.,

if y is in C

(x). Both  and < are called causality relations because they

establish a causal connection between the two events in the sense that the

event x can inﬂuence the event y either by way of the propagation of some

material phenomenon if x  y or some electromagnetic eﬀect if x<y.

Exercise 1.6.1 Prove that  is transitive, i.e., that x  y and y  z

implies x  z, and show by example that < is not transitive.

It is an interesting, and useful, fact that each of the relations  and < can

be deﬁned in terms of the other.

Lemma 1.6.1 For distinct points x and y in M,

x<yif and only if

)

x  y and

y  zimpliesx z.

Proof: First suppose x<y.ThenQ(y −x)=0sox  y is clear. Moreover,

if y  z,thenz − y is timelike and future-directed. Since y − x is null and

future-directed, Lemma 1.4.3 implies that z −x =(z −y)+(y −x)

is timelike

and future-directed, i.e., x  z.

For the converse we suppose x ≮ y and show that either x  y or there

exists a z in M with y  z, but x  z.Ifx ≮ y and x  y,theny−x is either

timelike and past-directed, null and past-directed or spacelike. In the ﬁrst case

any z with x<zhas the property that z −y =(z −x)+(x−y) is timelike and

future-directed (Lemma 1.4.3 again) so y  z, but x  z. Finally, suppose

y −x is either null and past-directed or spacelike (see Figure 1.6.1 (a) and (b)

espectively).Ineachcaseweproduceaz in M with y  z, but x  z in the

same way. Fix an admissible basis {e

} for M with x = x

and y = y

If y −x is null and past-directed, then x

−y

> 0. If y −x is spacelike we may

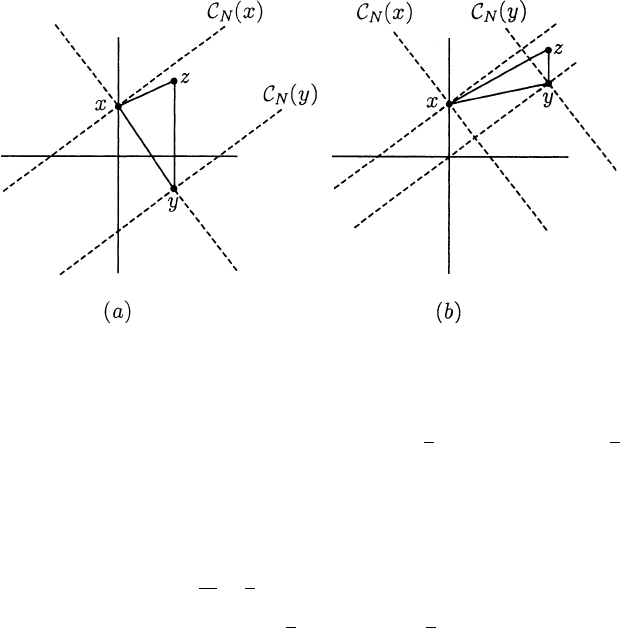
1.6 Causality Relations 59

Fig. 1.6.1

choose {e

} so that x

−y

> 0 (Exercise 1.5.2). Now, for each n =1, 2, 3,...,

deﬁne z

in M by z

= y

+ y





.Thenz

−y =

is timelike and future-directed so y  z

for each n. However,

Q(z

− x)=((z

− y)+(y −x))

= Q(z

− y)+2(z

− y) · (y − x)+Q(y − x)

= −

− y

)+Q(y − x)

= Q(y − x)+



2(x

− y

) −



Since Q(y −x) ≥ 0andx

−y

> 0 we can clearly choose n suﬃciently large

that Q(z

− x) > 0. For this n, z = z

satisﬁes y  z, but x  z. 

Exercise 1.6.2 Show that, for distinct x and y in M,

x  y if and only if

)

x ≮ y and

x<z<y for some z in M.

AmapF : M→Mis said to be a causal automorphism if it is one-to-one,

onto and both F and F

−1

preserve <, i.e., x<yif and only if F(x) <F(y).

Note that, in particular, F is not assumed to be linear (or even continuous).

We will eventually prove that this actually follows from the deﬁnition.

Exercise 1.6.3 Show that a one-to-one map F of M onto M is a causal

automorphism if and only if both F and F

−1

preserve , i.e., x  y if and

only if F (x)  F (y).

60 1 Geometrical Structure of M

We propose next to embark upon a proof of the remarkable result of

Zeeman [Z

] to which we referred in the Introduction.

For the statement

of the theorem we deﬁne a translation of M to be a map T : M→Mof

the form T (v)=v + v

for some ﬁxed v

in M and a dilation to be a map

K : M→Msuch that K(v)=kv for some positive real number k.Anor-

thogonal transformation L : M→Mis said to be orthochronous if x·Lx < 0

for all timelike or null and nonzero x.

Exercise 1.6.4 Show that any translation, dilation, orthochronous orthog-

onal transformation, or any composition of such mappings is a causal auto-

morphism.

Zeeman’s Theorem asserts that we have just enumerated them all.

Theorem 1.6.2 Let F : M→Mbe a causal automorphism of M.Then

there exists an orthochronous orthogonal transformation L : M→M,a

translation T : M→Mand a dilation K : M→Msuch that F = T ◦K ◦L.

For the proof we will require a sequence of ﬁve lemmas, the ﬁrst of which, at

least, is easy.

Lemma 1.6.3 A causal automorphism F : M→Mmaps light rays to light

rays. More precisely, if x<yand R

x,y

is the light ray through x and y,then

F (R

x,y

)=R

F (x),F (y)

Proof: Since both F and F

−1

preserve <, F maps null cones to null cones

so F (C

(x)) = C

(F (x)) and F (C

(y)) = C

(F (y)). By Theorem 1.2.2,

x,y

= C

(x) ∩C

(y)andR

F (x),F (y)

= C

(F (x)) ∩C

(F (y)). Thus,

F (R

x,y

)=F (C

(x) ∩C

(y))

= F(C

(x)) ∩ F (C

(y))

= C

(F (x)) ∩C

(F (y))

= R

F (x),F (y)



Lemma 1.6.4 A causal automorphism F : M→Mmaps parallel light rays

onto parallel light rays.

Proof: Let R

and R

be two distinct parallel light rays in M and P the

(2-dimensional) plane containing them. Any plane in M is the translation of

a plane through the origin which contains 0, 1 or 2 independent null vectors

(depending on whether the plane is outside the null cone to each of its points,

tangent to these null cones or intersects all of its time cones). Only the second

two cases are relevant to P however.

The proof is considerably more demanding than anything we have attempted thus far and

might reasonably be omitted on a ﬁrst reading.

1.6 Causality Relations 61

Suppose ﬁrst that P contains two independent null directions. Then it

contains two families {R

} and {S

} of light rays with all of the R

parallel

to R

and R

and all of the S

parallel to some light ray which intersects

both R

and R

. Thus, the families {F (R

)} and {F (S

)} are two families

of light rays in M with the following properties:

1. No two of the F(R

) intersect.

2. No two of the F(S

) intersect.

3. Each F (R

) intersects every F (S

To show that F (R

)andF (R

) are parallel it will suﬃce (since they do not

intersect) to show them coplanar. Suppose not. Then F (R

)andF (R

) lie

in some 3-dimensional aﬃne subspace R

of M. Since each F(S

) intersects

both F (R

)andF (R

), it too must lie in R

. Thus, by #3 above, all of the

F (R

)arecontainedinR

. We claim that, as a result, no F (R

)canbe

coplanar with either F (R

)orF (R

) (unless α =1orα = 2). For suppose

to the contrary that some F (R

) were coplanar with, say, F (R

). Every

F (S

) intersects both F (R

)andF (R

) so it too must lie in this plane.

Since F (R

) does not (by assumption) lie in this plane it can intersect the

plane in at most one point. Thus, F (R

) intersects at most one F (S

)and

this contradicts #3 above. Consequently, we may select an F (R

) such that

no two of {F (R

),F(R

)} are coplanar. Since {F (S

)} is then the

family of straight lines in R

intersecting all of {F (R

),F(R

)} it

is the family of generators (rulings) for a hyperboloid of one sheet in R

(this old, and none-too-well-known, result in analytic geometry is proved on

pages 105–106 of [Sa]). In the same way one shows that {F (R

)} is the other

family of rulings for this hyperboloid. But then each F (R

) would be parallel

to some F (S

) and this again contradicts #3 above.

Finally, we consider the case in which P contains only one independent

null direction (and so is tangent to each of its null cones). Any point in M has

through it a light ray parallel to both R

and R

. Since the tangent space to

the null cone at each point of R

is (only) 3-dimensional and since the same

is true of R

we may select a light ray R

parallel to both R

and R

and not

in either of these tangent spaces. Thus, the argument given above applies to

and R

as well as R

and R

.Consequently,F (R

)andF (R

)areboth

parallel to F (R

) and so are parallel to each other. 

Let R

x,y

= {x + r(y − x):r ∈ R} be a light ray and F (R

x,y

)={F (x)+

s(F (y) − F (x)) : s ∈ R} its image under F . We regard s as a function

of r : s = f(r). Our next objective is to show that f is linear, i.e., that

f(r + t)=f (r)+f(t)andf(tr)=tf (r) for all r and t in R. First though,

a few preliminaries. A map g : R

x,y

→ R

x,y

is called a translation of R

x,y

there exists a ﬁxed t in R such that

g(x + r(y −x)) = x +(r + t)(y −x)

62 1 Geometrical Structure of M

for all r in R. We shall say that a translation g of a light ray R lifts to F (R)

if there is a translation e : F (R) → F (R) such that the diagram

commutes, i.e., such that F ◦g = e ◦F . We show next that, in fact, every

translation of R lifts to F (R).

Lemma 1.6.5 Let R be a light ray, g:R → R a translation of R and F:M→

M a causal automorphism. Then g lifts to a translation e : F (R) → F (R)

of F (R).

Proof: For the proof we will construct a family of translations of R which

clearly do lift and then prove that this family exhausts all the translations

of R.

Select a light ray R

parallel to R and such that the plane of R and

contains two independent null directions. This plane therefore contains

a family {S

} of parallel light rays all of which meet R and R

. The family

} therefore determines an obvious parallel displacement map g

of R onto

(see Figure 1.6.2). Since F carries parallel light rays to parallel light rays

there is a parallel displacement e

of F (R)ontoF (R

) for which the diagram

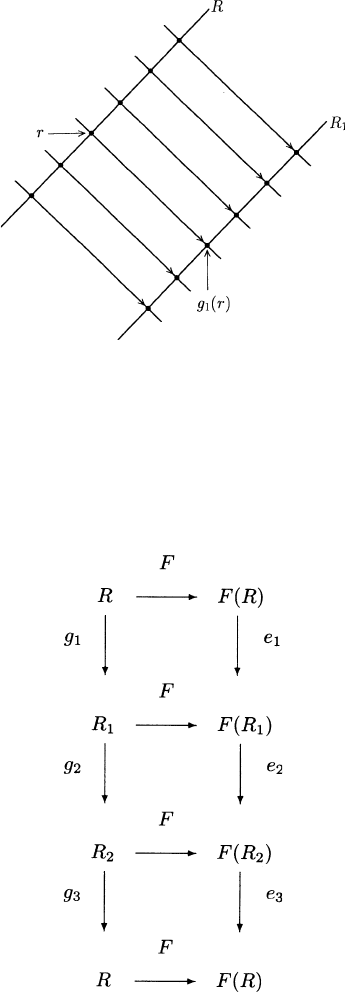
1.6 Causality Relations 63

Fig. 1.6.2

commutes. Now choose a light ray R

parallel to R

(and therefore to R)such

that the planes of R

and R

and of R and R

both contain two independent

null directions. Construct g

and g

as above so that all of the following

diagrams commute.

Now compose to get