Naber G.L. The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of the Special Theory of Relativity

Подождите немного. Документ загружается.

84 1 Geometrical Structure of M

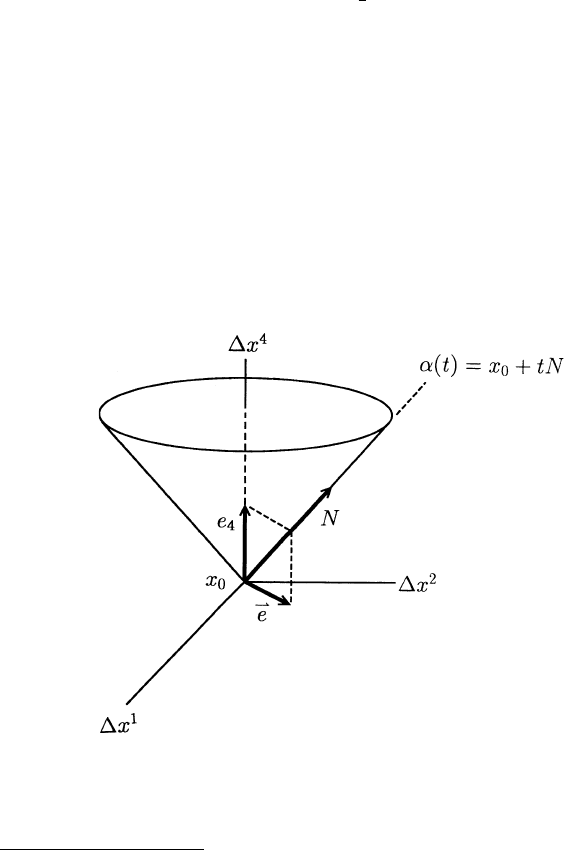
Exercise 1.8.3 Let N be a future-directed null vector in M and {e

} an

admissible basis with N = N

. Show that

N = (



+ e

), (1.8.7)

where  = −N · e

= N

and



is the direction 3-vector of N relative to

}, i.e.,



=((N

)

+(N

)

+(N

)

−

+ N

Now, we deﬁne a photon

in M to be a pair (α, N ), where N is a future-

directed null vector called the photon’s world momentum (or 4-momentum)

and α : I →M(I an interval in R containing 0) is given by α(t)=x

+ tN

for some ﬁxed event x

in M and all t in I. Relative to any admissible basis

} the positive real number

 = −N ·e

= N

is called the energy of (α, N ) in { e

} (see Figure 1.8.1). The frequency ν and

wavelength λ of (α, N)in{e

} are deﬁned by ν = /h and λ =1/ν,whereh

is a constant (called Planck’s constant).

Fig. 1.8.1

No quantum mechanical subtleties are to be inferred from our use of the term “photon”.

Our deﬁnition is intended to model any “massless” particle travelling at the speed of light.

1.8 Particles and Interactions 85

It is interesting to compare the energies of a photon (α, N )intwodiﬀerent

frames of reference. Thus, we let {e

} and {ˆe

} be two admissible bases

and write N = (



+ e

)=ˆ(



ˆe +ˆe

), where  = −N · e

and ˆ = −N · ˆe

Exercise 1.8.4 Show that ˆ = γ(1 − β(



)). Hint: Use Exercise 1.3.10.

But



and



both lie in the subspace spanned by e

and e

and the

restriction of the Lorentz inner product to this subspace is just the usual

positive deﬁnite inner product on R

.Thus,



=cosθ,whereθ is the

angle in



(the spatial coordinate system of the frame corresponding to {e

})

between the direction of the photon and the direction of



. We therefore

obtain

ˆ



ˆν

= γ(1 − β cos θ)=

1 − β cos θ



1 − β

(1.8.8)

which is the relativistic formula for the Doppler eﬀect. Using the binomial

expansion (1.8.2)forγ gives

ˆ



ˆν

=(1−β cos θ)+

(1 − β cos θ)+··· . (1.8.9)

The ﬁrst term 1−β cos θ is the familiar classical formula for the Doppler eﬀect,

whereas the remaining terms constitute the relativistic correction contributed

by time dilation. Three special cases of (1.8.8) are of particular interest.

θ =0(so



)=⇒

ˆν



1 − β

1+β

, (1.8.10)

θ = π(so



= −



)=⇒

ˆν



1+β

1 − β

, (1.8.11)

θ =

(so



=0)=⇒

ˆν



1 − β

. (1.8.12)

The classical theory predicts no Doppler shift in the case θ = π/2sothat

the formula (1.8.12) for the so-called t

ansverse

Doppler eﬀect represents a

purely relativistic phenomenon. Experimental veriﬁcation of (1.8.12)wasﬁrst

cco

mplished b

y Ives and Stilwell [IS] and is regarded as direct conﬁrmation

the r

eality of time dilation.

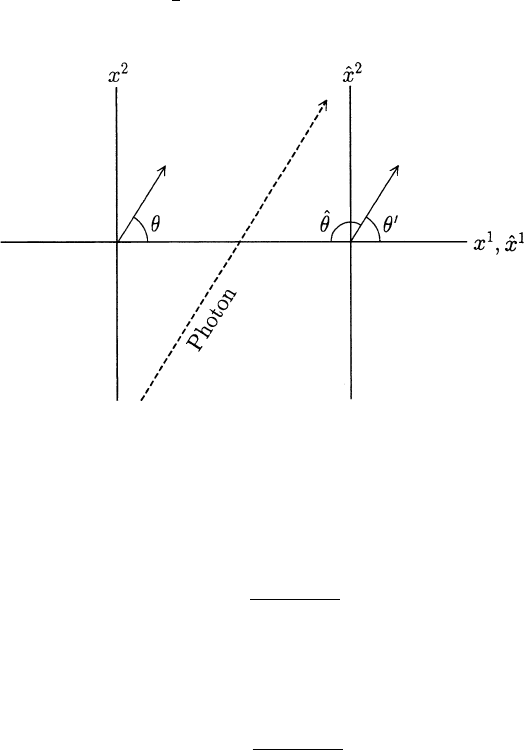
Next we wish to compare the angles θ and

θ deﬁned by cos θ =



and cos

θ =



ˆe ·



d .

Exercise 1.8.5 Let



ˆu denote the velocity 3-vector of S relative to

((1.3.12)and(1.3.15)) and show that



ˆu = −γβ(



+ βe

). (1.8.13)

86 1 Geometrical Structure of M

From (1.8.13) we conclude that



d = −γ(



+ βe

). (1.8.14)

Since N = (



+ e

)=ˆ(



ˆe +ˆe

) we obtain from the deﬁnitions of θ and



·N =  cos θ and



d · N =ˆ cos

θ. (1.8.15)

Now, ˆ cos

θ =



d ·N = −γ(



·N + βe

·N )=−γ( cos θ −β)=−γcos θ +

γβ.Thus,

ˆ



cos

θ = γ(β −cos θ)

Fig. 1.8.2

which, by (1.8.8), we may write as

γ(1 − β cos θ)cos

θ = γ(β −cos θ),

cos

θ =

β −cos θ

1 − β cos θ

. (1.8.16)

Generally, however, one would be more interested in comparing the angles θ

and θ



= π −

θ, e.g., when the spatial axes are in standard orientation as in

Figure 1.8.2. Since cos θ



= −cos

θ,(1.8.16) becomes the standard relativistic

aberration formula

cos θ



cos θ − β

1 − β cos θ

. (1.8.17)

At this point we have assembled enough machinery to study some of the

physical interactions to which the special theory of relativity is routinely

1.8 Particles and Interactions 87

applied. Henceforth, we shall use the term free particle to refer to either a

free material particle or a photon. If A is a ﬁnite set of free particles, then

each element of A has a unique world momentum vector. The sum of these

vectors is called the total world momentum (or total 4-momentum) of A.

A contact interaction in M is a triple (A,x,

A), where A and

A are two

ﬁnite sets of free particles, neither of which contains a pair of particles with

linearly dependent world momenta, and x is an event such that

(a) x is the terminal point of all the particles in A (i.e., for each (α, m)inA

with α :[a, b] →M,wehaveα(b)=x),

(b) x is the initial point of all the particles in

A,and

Intuitively, the event x should be regarded as the collision of all the particles

in A, from which emerge all the particles in

A (which may be physically

quite diﬀerent than those in A, e.g., it has been observed that the collision of

two electrons can result in three electrons and a positron). The prohibition

on pairs of particles with linearly dependent world momenta in the same set

is based on the presumption that two such particles would be physically in-

distinguishable. Property (c) is called the conservation of world momentum

and contains the appropriate relativistic generalizations of two classical con-

servation principles: the conservation of momentum and the conservation of

energy.

Several conclusions concerning contact interactions can be drawn directly

from the results we have available. Consider, for example, an interaction

(A,x,

A)inwhich

A consists of a single photon. Then the total world mo-

mentum of

A isnullsothesamemustbetrueofA.

Since the world momenta

of the

individual particles in A are all either timelike or null and all are future-

directed, Lemma 1.4.3 implies that all of these world momenta must be null

and parallel. Since A cannot contain two distinct photons with parallel world

momenta, A must also consist of a single photon which, by (c), must have the

same world momentum as the photon in

A. In essence, “nothing happened

at x”. We conclude that no nontrivial interaction of the type modelled by our

deﬁnition can result in a single photon and nothing else.

A contact interaction (A,x,

A) is called a disintegration or decay if A

consists of a single free particle.

Exercise 1.8.6 Analyze a disintegration (A,x,

A)inwhichA consists of a

single photon.

Suppose that A consists of a single free material particle of proper mass

and

A consists of two material particles with proper masses m

and m

(such disintegrations do, in fact, occur in nature, e.g., in α-emission). Let

and P

be the world momenta of the particles with masses m

and m

respectively. Appealing to (1.8.1), the Reversed Triangle Inequality

88 1 Geometrical Structure of M

(Theorem 1.4.2) and the fact that P

and P

are linearly independent we

ﬁnd that

+ m

. (1.8.18)

The excess mass m

− (m

+ m

) of the initial particle is regarded as a

measure of the amount of energy required to split m

into two pieces. Stated

somewhat diﬀerently, when the two particles in

A were held together to form

the single particle in A the “binding energy” contributed to the mass of this

latter particle, while, after the decay, the diﬀerence in mass appears in the

form of kinetic energy of the generated particles.

Exercise 1.8.7 Show that a free electron cannot emit or absorb a photon.

Hint: The contradiction arises from the constancy of the proper mass m

of an electron. A more complicated system such as an atom or molecule

whose proper mass can vary with its energy state (these being determined

by the principles of quantum mechanics) is not prohibited from absorbing or

emitting photons.

Next we consider two examples of more detailed calculations for speciﬁc

interactions, each of which models an important reaction in particle physics.

We should emphasize at the outset, however, that the conservation of world

momentum alone is almost never suﬃcient to determine all of the details of

the resulting motion. Additional conservation laws (e.g., of “spin”) can reduce

the degree of indeterminacy, but quantum mechanics imposes a positive lower

bound on the extent to which this is possible. As ﬁnal preparation for our

examples we will need to record the conservation of world momentum in

component form relative to an arbitrary admissible basis {e

}.Thuswewrite



mγu



hνe



˜m˜γ ˜u



h˜ν˜e

,i=1, 2, 3, (1.8.19)



mγ +



hν =



˜m˜γ +



h˜ν, (1.8.20)

where the ﬁrst and third sums in each are over all the material particles in

A and

A respectively, whereas the second and fourth sums are over all of the

photons in A and

A respectively.

In our ﬁrst example we describe the so-called Compton eﬀect. The physical

situation we propose to model is the following: A photon collides with an

electron and rebounds from it (generally with a diﬀerent frequency), while

the electron recoils from the collision. Thus, we consider a contact interaction

(A,x,

A), where A consists of a photon with world momentum N and a

material particle with proper mass m

and world velocity U and

A consists

of a photon with world momentum

N and a material particle with proper

mass m

and world velocity

U. We analyze the interaction in a frame of

reference in which the material particle in A is at rest (time axis parallel

to the worldline of the particle). In this frame the conservation of world

momentum equations (1.8.19)and(1.8.20) become (since u

=0,γ=1)

1.8 Particles and Interactions 89

Fig. 1.8.3

˜γ ˜u

+ h˜ν˜e

= hνe

,i=1, 2, 3, (1.8.21)

˜γ + h˜ν = m

+ hν. (1.8.22)

Let ξ =˜ν/ν and k = hν/m

.Wedenotebyθ the angle between the direction

vectors of the two photons in the given frame of reference, i.e., cos θ = e

˜e

+ e

˜e

(see Figure 1.8.3). With this notation (1.8.21)and(1.8.22)can

be written

˜γ ˜u

= ke

− ξk˜e

,i=1, 2, 3, (1.8.23)

˜γ − 1=k(1 − ξ). (1.8.24)

Since

=(˜u

)

+(˜u

)

+(˜u

)

=1− ˜γ

−2

, when we (Euclidean) dot each

side of (1.8.23)withitselfweobtain

˜γ

= k

(1 − 2ξ cos θ + ξ

)=˜γ

− 1.

Thus,

˜γ +1=

(1 − 2ξ cos θ + ξ

)

˜γ − 1

k(1 − 2ξ cos θ + ξ

)

1 − ξ

(1.8.25)

by (1.8.24). Subtracting (1.8.24)from(1.8.25)wenextobtain

k(1 − 2ξ cos θ + ξ

) − k(1 − ξ)

1 − ξ

k(2ξ − 2ξ cos θ)

1 − ξ

2kξ(1 − cos θ)

1 − ξ

4kξ sin





1 − ξ

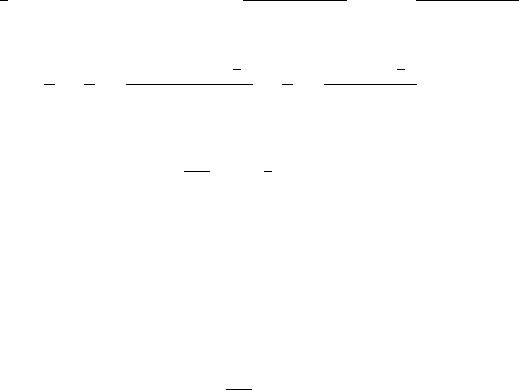
90 1 Geometrical Structure of M

Thus, 2kξ sin





=1−ξ and therefore ξ =

1+2k sin

(θ/2)

so ˜ν =

1+2k sin

(θ/2)

From this we compute

λ − λ =

˜ν

−

1+2k sin





−

2k sin





We conclude that

λ − λ =

sin





(1.8.26)

which gives the change in wavelength of the photon as a function of the angle

θ through which it is deﬂected (in the frame in which the electron is initially

at rest). Observe that this change in wavelength does not depend on the

wavelength λ of the incident photon, but only on the angle through which

it is deﬂected. Moreover, this diﬀerence ranges from a minimum of 0 when

θ = 0 (the photon and electron do not interact physically) to a maximum of

Δλ

max

(1.8.27)

when θ = π (the photon is thrown straight back). This maximum change in

wavelength is a characteristic feature of the electron; the quantity h/m

called the Compton wavelength of the electron.

Next we consider an inelastic collision between two material particles.

The situation we have in mind is as follows: two free material particles with

masses m

and m

collide and coalesce to form a third material particle of

mass m

. Classically it is assumed that m

= m

and on the basis of this

assumption (and the conservation of Newtonian momentum) one ﬁnds that

kinetic energy is lost during the collision. In Newtonian mechanics this lost

kinetic energy disappears entirely from the mechanical picture in the sense

that it is viewed as having taken the form of heat in the combined particle and

therefore cannot be discussed further by the methods of mechanics. We shall

see that this rather unsatisfactory feature of Newtonian mechanics is avoided

in relativistic mechanics by observing that conservation of world momentum

(which includes the conservation of energy) requires that the “hot” combined

particle have a proper mass which is greater than the sum of the two masses

from which it is formed, the diﬀerence m

− (m

+ m

) being a measure of

the energy required to bind the two particles together; this energy “acts like

mass” in the combined particle.

We shall therefore consider a contact interaction (A,x,

A), where A con-

sists of two free material particles with proper masses m

and m

and world

velocities U

and U

respectively and

A consists of one free material particle

with proper mass m

and world velocity U

. Conservation of world momen-

tum requires that

= m

+ m

. (1.8.28)

1.8 Particles and Interactions 91

Again observe that the Reversed Triangle Inequality (Theorem 1.4.2) gives

+ m

.Moreover,sinceU

· U

= U

· U

= U

· U

= −1weobtain

(by dotting both sides of (1.8.28) with itself and using any admissible frame

ref

erence)

= m

+ m

− 2m

· U

= m

+ m

− 2m

(



, 1) · (



, 1), (1.8.29)

= m

+ m

+2m

(1 −



which yields the resultant mass m

in terms of m

and the quantities u

and u

,i=1, 2, 3, which can be measured in the given frame of reference.

From (1.8.28) one can then compute U

We wish to obtain an approximate formula for m

which can be compared

with the Newtonian expression for the loss in kinetic energy. Assume that β

and β

are small so that γ

and γ

are approximately 1 (the frame of reference

is then no longer arbitrary, of course). We will eventually take γ

≈ 1, but

ﬁrst we consider the somewhat better approximations

≈ 1+

,j=1, 2,

obtained from the binomial expansion (1.8.2). Then

≈







=1+

≈ 1+

. (1.8.30)

Exercise 1.8.8 Show that (1.8.29)and(1.8.30) yield

≈ (m

+ m

)

+ m



+ β

− 2γ

(



)



. (1.8.31)

Now taking γ

≈ 1in(1.8.31)weobtain

≈ (m

+ m

)

+ m



, (1.8.32)

where |



is the squared magnitude of the relative velocity



−



of the two particles in A as measured in the given frame. From (1.8.32)we

obtain

≈ m

+ m



Assuming that m

≈ m

+ m

in the denominator we arrive at

≈ m

+ m



, (1.8.33)

where the last term represents the approximate gain in proper mass as a

result of the collision.

92 1 Geometrical Structure of M

Now, in Newtonian mechanics it is assumed that m

= m

+ m

so that

conservation of Newtonian momentum requires that

+ m

)



= m



+ m



. (1.8.34)

Taking the Euclidean dot product of each side of (1.8.34)withitselfthen

yields

+ m

)



= m



+ m



+2m

(



). (1.8.35)

Exercise 1.8.9 Use (1.8.35) to show that the classical loss in kinetic energy

due to

the c

ollision is given by



−

+ m



+ m



where |



= |



−



Consequently, the Newtonian expression for the lost kinetic energy coincides

with the relativistic formula (1.8.33) for the approximate gain in proper mass

combined particle.

Chapter 2

Skew-Symmetric Linear

Transformations and

Electromagnetic Fields

2.1 Motivation via the Lorentz Law

A charged particle in M is a triple (α, m, e), where (α, m)isamaterial

particle and e is a nonzero real number called the charge of the particle.

A free charged particle is a charged particle (α, m, e), where (α, m)isafree

material particle. Charged particles do two things of interest to us. By their

very presence they create electromagnetic ﬁelds and they also respond to the

ﬁelds created by other charges. Our objective in this chapter is to isolate the

appropriate mathematical object with which to model an electromagnetic

ﬁeld in M , derive many of its basic properties and then investigate these two

activities.

Charged particles “respond” to the presence of an electromagnetic ﬁeld

by experiencing changes in world momentum. The quantitative nature of

this response is expressed by a diﬀerential equation relating the proper time

derivative of the particle’s world momentum to the ﬁeld. This equation of

motion is generally taken to be the so-called Lorentz World Force Law (or

Lorentz 4-Force Law ) which expresses the rate at which the particle’s world

momentum changes at each point on the worldline as a linear function of the

particle’s world velocity:

dτ

= eFU , (2.1.1)

where U = U(τ) is the particle’s world velocity, P = mU its world momentum

and, at each point, F : M→Mis a linear transformation deﬁned in terms of

the classical “electric and magnetic 3-vectors



and



”atthatpoint((2.1.1)

is an abbreviated version of the somewhat more accurate and considerably

more cumbersome

dP(τ )

dτ

= eF

α(τ )

(U(τ)), where F

α(τ )

is the appropriate

linear transformation at α(τ) ∈M). We should point out that (2.1.1)can

be regarded as an appropriate equation of motion for charged particles in an

, : An Introduction

, Applied Mathematical Sciences 92,

G.L. Naber The Geometry of Minkowski Spacetime to the Mathematics

of the Special Theory of Relativity