Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

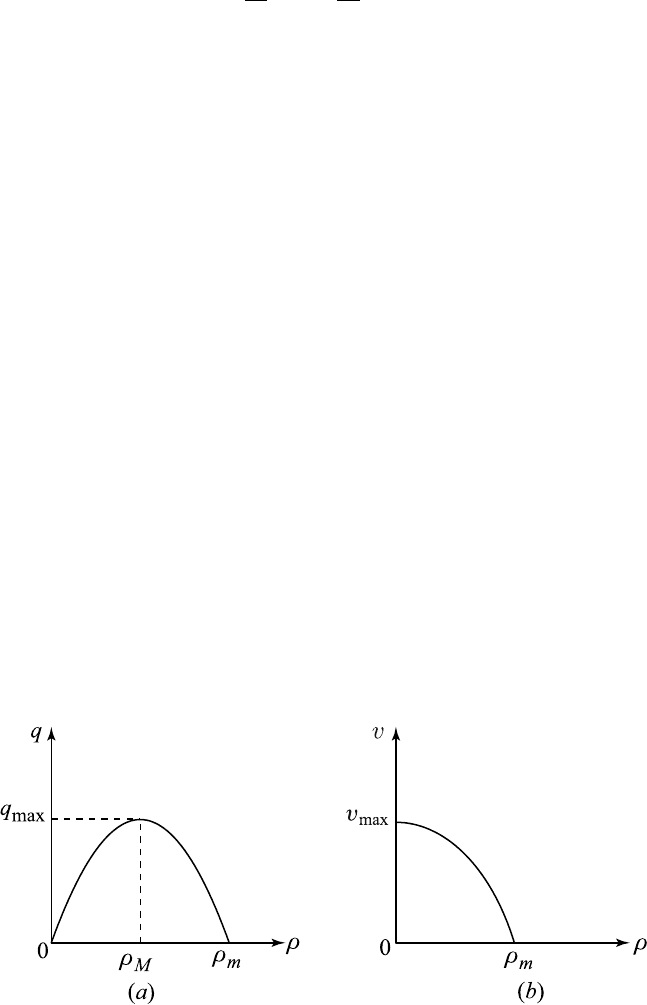
13.6 The Traﬃc Flow Model 551

∂ρ

∂t

+ c (ρ)

∂ρ

∂x

=0, (13.6.6)

where

c (ρ)=q

′

(ρ)=v + ρv

′

(ρ) . (13.6.7)

In general, the local velocity v (ρ) is a decreasing fun ction of ρ so that

v (ρ) has a ﬁnite maximum value v

max

at ρ = 0 and decreases to zero at

ρ = ρ

max

= ρ

. For the value of ρ = ρ

, the cars are bumper to bumper.

Since q = ρv, q (ρ)=0whenρ = 0 and ρ = ρ

. This means that q is an

increasing function of ρ until it attains a maximum value q

max

= q

for

some ρ = ρ

and then decreases to zero at ρ = ρ

. Both q (ρ)andv (ρ)

are shown in Fi gure 13.6.1.

Equation (13.6.6) is similar to (13.2.1) with the wave propagation ve-

locity c (ρ)=v (ρ)+ρv

′

(ρ). Since v

′

(ρ) < 0, c (ρ) <v(ρ), that is, the

propagation velocity is less than the car velocity. In other words, waves

propagate backwards through the stream of cars, and drivers are warned of

disturbances ahead. It follows from Figure 13.6.1a that q (ρ) is an i ncreasing

function in [0,ρ

], a decreasing function in [ρ

,ρ

], and attains a max-

imum at ρ

. Hence, c (ρ)=q

′

(ρ) is positive in [0,ρ

], zero at ρ

and

negative in [ρ

,ρ

]. All these mean that waves propagate forward relative

to the highway in [0,ρ

], are stationary at ρ

, and then travel backwards

in [ρ

,ρ

We use Section 13.1 to solve the initial-value problem for the nonlinear

equation (13.6.6) with the initial condition ρ (x, 0) = f (x). The solution is

ρ (x, t)=f (ξ) ,x= ξ + tF (ξ) , (13.6.8)

where

F (ξ)=c (f (ξ)) .

Figure 13.6.1 Graphs of q (ρ) and v (ρ).

552 13 Nonlinear Partial Diﬀerential Equations with Applications

Since c

′

(ρ)=q

′′

(ρ) < 0, q (ρ) is convex, and c (ρ) is a decreasing function

of ρ. This means that breaking occurs at the left due to formation of sho ck

at the back. Waves propagate slower than the cars, so drivers enter such

a l ocal density increase from behind; they must decelerate rapidly through

the shock but speed up slowly as they get out from the crowded area. These

conclusions are in accord with observational results.

Actual observational data of traﬃc ﬂ ow indicate that a typical result

on a single lane highway is ρ

≈ 225 cars per mile, ρ

≈ 80 cars per mile,

and q

≈ 1590 cars p er hou r. Thus, the maximum ﬂow rate q

occurs at

alowvelocityv = q

/ρ

≈ 20 miles per hour.

13.7 Flood Waves in Rivers

We consider ﬂood waves in a long rectangular r iver of constant breadth. We

take the x-axis along the river which ﬂows in the positive x-direction and

assume that the disturbance is approximately the same across the breadth.

In this problem, the depth h (x, t) of the river plays the role of density in

the traﬃc ﬂow model discussed in Section 13.6. Let q (x, t) be the ﬂow per

unit breadth and per unit time. According to the Conservation Law, the

rate of change of the mass of the ﬂuid in any section x

≤ x ≤ x

must be

balanced by the net ﬂux across x

and x

so that the conservation equation

becomes



h (x, t) dx + q (x

,t) − q (x

,t)=0. (13.7.1)

An argument similar to the previous section gives

∂h

∂t

∂q

∂x

=0. (13.7.2)

Although the ﬂuid ﬂow is extremely complicated, we assume a simple func-

tion relation q = Q (h) as a ﬁrst approximation to express the increase in

ﬂow as the water level arises. Thus, equation (13.7.2) becomes

+ c (h) h

=0, (13.7.3)

where c (h)=Q

′

(h)andQ (h) is determined from the balance between the

gravitational force and the frictional force of the river bed. This equation

is similar to (13.2.1) and the method of solution has already been obtained

in Section 13.2.

Here we discuss the velocity of wave propagation for some particular

values of Q (h). One such result is given by the Chezy result as

Q (h)=hv, (13.7.4)

13.8 Riemann’s Simple Waves of Finite Amplitude 553

where v = α

√

h is the velocity of ﬂuid ﬂow and α is a constant, so that the

propagation velocity of ﬂood waves is given by

c (h)=Q

′

(h)=

√

h =

v. (13.7.5)

Thus, the ﬂood waves propagate one and a half times faster than the stream

velocity .

For a general case where v = αh

Q (h)=hv = αh

n+1

, (13.7.6)

so the propagation velocity of ﬂood waves is

c (h)=Q

′

(h)=(n +1)v. (13.7.7)

This result also indicates that ﬂood waves propagate faster than the ﬂuid.

13.8 Riemann’s Simple Waves of Finite Amplitude

We consider a one-dimensional unsteady isentropic ﬂow of gas of density

ρ and pressure p with the direction of motion along the x-axis. Suppose

u (x , t)isthex-component of the velocity at time t and A is an area-

element of the (y, z)-plane. The volume of the rectangular cylinder of height

dx standing on the element A is then Adx and its mass Aρ

dx dt is

determined by the mass entering it, which is equal to −A (∂/∂x)(ρu) dx dt.

Its acceleration is (u

+ uu

) and the force impelling it in the p ositive x-

direction is −p

Adx= −c

Adx,wherep = f (ρ)andc

= f

′

(ρ). These

results lead to two coupled nonlin ear partial diﬀerential equations

∂ρ

∂t

∂

∂x

(ρu)=0, (13.8.1)

+ uu

=0. (13.8.2)

In matrix form, this system is

∂U

∂x

+ I

∂U

∂t

=0, (13.8.3)

where U, A and I are matrices given by

U =

⎛

⎝

⎞

⎠

,A=

⎛

⎝

uρ

/ρ u

⎞

⎠

and I =

⎛

⎝

⎞

⎠

. (13.8.4)

The concept of characteristic curves introduced brieﬂy in Section 13.2

requires generali zation if it is to be applied to quasi-linear systems of ﬁrst-

order partial diﬀerential equations (13.8.1)–(13.8.2).

554 13 Nonlinear Partial Diﬀerential Equations with Applications

It is of interest to determine how a solution evolves with time t. Hence,

we leave the time variable unchanged and replace the space variable x by

some arbitrary curvilinear coordinate ξ so that the semi-curvilinear coor-

dinate transformation from (x, t)to(ξ, t

′

) can be introduced by

ξ = ξ (x, t) ,t

′

= t. (13.8.5)

If the Jacobian of this transformation is nonzero, we can transform

(13.8.3) by the following correspondence rule:

∂

∂t

≡

∂ξ

∂t

∂

∂ξ

∂t

′

∂t

∂

∂t

′

∂ξ

∂t

∂

∂ξ

∂

∂t

′

∂

∂x

≡

∂ξ

∂x

∂

∂ξ

∂t

′

∂x

∂

∂t

′

∂ξ

∂x

∂

∂ξ

This rule transforms (13.8.3) into the form

∂U

∂t

′



∂ξ

∂t

I +

∂ξ

∂x



∂U

∂ξ

=0. (13.8.6)

This equation can be used to determine ∂U/∂ξ provided that the de-

terminant of its coeﬃcient matrix is non-zero. Obviously, this condition de-

pends on the nature of th e curvilinear coordinate curves ξ (x, t) = constant,

which has been kept arbitrary. We assume now that the determinant van-

ishes for the particular choice ξ = η so that



∂η

∂t

I +

∂η

∂x



=0. (13.8.7)

In view of this, ∂U/∂η will become indeterminate on the family of curves

η = constant, and hence, ∂U/∂η may be discontinuous across the curves

η = constant. This implies that each element of ∂U/∂η will be discontinuou s

across any of the curves η = constant. It is then necessary to ﬁnd out how

these discontinuities in the elements of ∂U/∂η are related across the curve

η = constant. We next consider the solutions U which are everywhere con-

tinuous with discontinuous derivatives ∂U/∂η across the particular curve

η = constant = η

.SinceU is continuous, elements of the matrix A are not

discontinuous across η = η

so that A can be determined in the neighbor-

hood of a point P on η = η

. And sin ce ∂U/∂t

′

is continuous everywhere,

it is continuous across the curve η = η

at P .

In view of all of the above facts, it follows that diﬀerential equation

(13.8.6) across the curve ξ = η = η

at P becomes



∂η

∂t

I +

∂η

∂x





∂U

∂η



=0, (13.8.8)

where [f]

= f (P +)−f (P −) denotes the discontinuous jump in the quan-

tity f across the curve η = η

,andf (P −)andf (P +) represent the values

13.8 Riemann’s Simple Waves of Finite Amplitude 555

to the immediate left and immediate right of the curve at P .SinceP is

any arbitrary point on the curve, ∂/∂η denotes the diﬀerentiation normal

to the curves η = constant so that equation (13.8.8) can be regarded as the

compatibility condition satisﬁed by ∂U/∂η on either side of and normal to

these curves in the (x, t)-plane.

Obviously, equation (13.8.8) is a homogeneous system of equations for

the two jump quantities [∂U/∂η]. Therefore, for the existence of a non-

trivial solution, the coeﬃcient determinant must vanish, that is,



∂η

∂t

I +

∂η

∂x



=0. (13.8.9)

However, along the curves η = constant, we have

0=dη = η





, (13.8.10)

so that these curves have the constant slope, λ

= −

= λ. (13.8.11)

Consequently, equations (13.8.9) and (13.8.8) can be expressed in terms of

λ in the form

|A − λI| =0, (13.8.12)

(A − λI)



∂U

∂η



=0, (13.8.13)

where λ represents the eigenvalues of the matrix A,and[∂U/∂η] is propor-

tional to the corresponding right eigenvector of A.

Since A is a 2 ×2 matrix, it must have two eigenvalues. If these are real

and d istin ct, integration of (13.8.11) leads to two distinct families of real

curves Γ

and Γ

in the (x, t)-plane:

= λ

,r=1, 2. (13.8.14)

The families of curves Γ

are called the characteristic curves of the system

(13.8.3). Any one of these famili es of curves Γ

may be chosen for the

curvilinear coordinate curves η = constant. The eigenvalues λ

have the

dimensions of velocity, and the λ

associated with each family will then be

the velocity of propagation of the matrix column vector [∂U/∂η] along the

curves Γ

belonging to that family.

In this particular case, the eigenvalues λ of the matrix A are determined

by (13.8.12), that is,



u − λρ

/ρ u − λ



=0, (13.8.15)

556 13 Nonlinear Partial Diﬀerential Equations with Applications

so that

λ = λ

= u+

c, r =1, 2. (13.8.16)

Consequently, the families of the characteristic curves Γ

(r =1, 2) deﬁned

by (13.8.14) become

= u + c, and Γ

= u − c. (13.8.17)

In physical terms, these results indicate that disturbances propagate

with the sum of the velocities of the ﬂuid and sound along the family of

curves Γ

. In the second family Γ

, they propagate with the diﬀerence of

the ﬂuid velocity u and the sound velocity c.

The right eigenvectors µ

≡

⎛

⎜

⎝

(1)

(2)

⎞

⎟

⎠

are solutions of the equations

(A − λ

I) µ

=0,r=1, 2, (13.8.18)

or,

⎛

⎝

u − λ

/ρ u − λ

⎞

⎠

⎛

⎜

⎝

(1)

(2)

⎞

⎟

⎠

=0,r=1, 2. (13.8.19)

This result combined with (13.8.13) gives

⎛

⎝

[ρ

]

⎞

⎠

⎛

⎜

⎝

(1)

(2)

⎞

⎟

⎠

= α

⎛

⎝

c/ρ

⎞

⎠

,r=1, 2, (13.8.20)

where α is a constant.

In other words, across a wavefront in the Γ

family of characteristic

curves,

[∂ρ/∂η]

[∂u/∂η]

c/ρ

, (13.8.21)

and across a wavefront in the Γ

family of ch aracteristic curves,

[∂ρ/∂η]

[∂u/∂η]

−c/ρ

, (13.8.22)

where c and ρ have values appropriate to the wavefront.

The above method of characteristics can be applied to a more general

system

13.8 Riemann’s Simple Waves of Finite Amplitude 557

∂U

∂t

+ A

∂U

∂x

=0, (13.8.23)

where U is an n ×1 matrix with elements u

, u

, ..., u

and A is an n ×n

matrix with elements a

. An argument similar to that given above leads

to n eigenvalues of (13.8.13). If these eigenvalues are real and distinct,

integration of equations (13.8.14) with r =1,2,..., n gives n distinct

families of real curves Γ

in the (x, t)-plane so that

= λ

,r=1, 2,...n. (13.8.24)

When the eigenvalues λ

of A are all real and distinct, there are n dis-

tinct linearly independent right eigenvectors µ

of A satisfying the equation

Aµ

= λ

where µ

is an n ×1 matrix with elements µ

(1)

, µ

(2)

, ..., µ

(n)

. Then across

awavefrontbelongingtotheΓ

family of char acteristics, it turns out that

[∂u

/∂η]

(1)

[∂u

/∂η]

(2)

= ...=

[∂u

/∂η]

(n)

, (13.8.25)

where the elements of µ

are known on the wavefront.

In order to introduce the Riemann invariants, we form the linear com-

bination of the eigenvectors (+

c/ρ, 1) with equations (13.8.1)–(13.8.2) to

obtain

(ρ

+ ρu

+ uρ



+ uu



=0. (13.8.26)

We use ∂u/∂ρ =+

c/ρ from (13.8.21)–(13.8.22) and rewrite (13.8.26) as

[ρ

+(u +

c) ρ

]+[u

+(u + c) u

]=0. (13.8.27)

In view of (13.8.17), equation (13.8.27) becomes

du +

dρ =0 on Γ

,r=1, 2, (13.8.28)

or,

d [F (ρ)+

u]=0 on Γ

, (13.8.29)

where

F (ρ)=



c (ρ)

dρ. (13.8.30)

Integration of (13.8.29) gives

558 13 Nonlinear Partial Diﬀerential Equations with Applications

F (ρ)+u =2r on Γ

and F (ρ) − u =2s on Γ

, (13.8.31)

where 2r and 2s are constants of integration on Γ

and Γ

, respectively.

The quantities r and s are called the Riemann invariants. As stated

above, r is an arbitrary constant on characteristics Γ

, an d hence, in general,

r will vary on each Γ

. Similarly, s is constant on each Γ

but will vary on

.Itisnaturaltointroducer and s as new curvilinear coordinates. Since r

is constant on Γ

, s can be treated as the parameter on Γ

. Similarly, r can

be regarded as the parameter on Γ

. Then, dx =(u +

c) dt on Γ

implies

that

=(u + c)

on Γ

, (13.8.32)

=(u − c)

on Γ

. (13.8.33)

In fact, r is a constant on Γ

,ands is a constant on Γ

. Therefore, the

derivatives in the two equations are really partial derivations with respect

to s and r so that we can rewrite them as

∂x

∂s

=(u + c)

∂t

∂s

, (13.8.34)

∂x

∂r

=(u − c)

∂t

∂r

. (13.8.35)

These two ﬁrst-order PDE’s can, in general, be solved for x = x (r, s),

t = t (r, s), and then, by inversion, r and s as functions x and t can be

obtained. Once this is done, we use (13.8.31) to determine u (x, t)andρ (x, t)

in terms of r and s as

u (x , t)=r − s, F (ρ)=r + s. ( 13.8.36)

When one of the Riemann invariants r and s is constant throughout

the ﬂow, the corresponding solution is tremendously simpliﬁed. The solu-

tions are known as simple wave motions representing simple waves in one

direction only. The generating mechanisms of simple waves with their pr op-

agation laws can be illustrated by the piston problem in gas dynamics.

Example 13.8.1. Determine the Riemann invariants for a polytropic gas

characterized by the law p = kρ

,wherek and γ are constants.

In this case

dρ

= kγ ρ

γ−1

,F(ρ)=



c (ρ)

γ − 1

Hence, the Riemann invariants are given by



γ − 1



c +

u =(2r, 2s)onΓ

. (13.8.37)

13.8 Riemann’s Simple Waves of Finite Amplitude 559

It is also possible to express the dependent variables u and c in terms

of the Riemann invariants. It turns out that

u = r − s, c =

γ − 1

(r + s) . (13.8.38)

Example 13.8.2. (The Piston Problem in a Polytropic Gas). The problem

is to determine how a simple wave is produced by the prescribed motion of

a piston in the closed end of a semi-inﬁnite tube ﬁlled with gas.

This is a one-dimensional unsteady problem in gas dynamics. We assume

that the gas is initially at rest with a uniform state u =0,ρ = ρ

,and

c = c

. The piston starts from rest at th e origin and is allowed to withdraw

from the tu be with a variable velocity f or a time t

, after which the velocity

of withdrawal r emains constant. The piston path is shown by a dotted

curve in Figure 13.8.1. In the (x, t)-plane, the path of the piston is given

by x = X (t)withX (0) = 0. The ﬂuid velocity u is equal to the piston

velocity

X (t) on the piston x = X (t), which will be used as the boundary

condition for the piston.

The initial state of the gas is given by u = u

, ρ = ρ

,andc = c

at t =0,inx ≥ 0. The characteristic line Γ

that bounds it and passes

through the origin is determined by the equation

=(u + c)

t=0

= c

so that the equation of the characteristic line Γ

is x = c

Figure 13.8.1 Simple waves generated by the motion of a piston.

560 13 Nonlinear Partial Diﬀerential Equations with Applications

In v iew of the uniform initial state, all the Γ

characteristics start on

the x-axis so that the Riemann invariants s in (12.8.37b) must be constant

andoftheform

γ − 1

− u =

γ − 1

, (13.8.39)

or,

u =

2(c − c

)

γ − 1

,c= c

(γ − 1)

u. (13.8.40ab)

The characteristics Γ

meeting the piston are given by

γ − 1

+ u =2r on each Γ

and Γ

= u + c, (13.8.41)

which is, since (13.8.40ab ) holds everywhere,

u = constant on Γ

and Γ

= c

(γ +1)u. (13.8.42)

Since the ﬂow is continuous with no shocks, u = 0 and c = c

ahead of

and on Γ

, which separates those Γ

meeting the x-axis from those meet-

ing the piston. The family of lines Γ

through the origin has the equation

(dx/dt)=ξ,whereξ is a parameter with ξ = c

on Γ

.TheΓ

characteris-

tics are also deﬁned by (dx/dt)=u+c so that ξ = u+c. Hence, elimination

of c from (13.8.40b) gives

u =



γ +1



(ξ − c

) . (13.8.43)

Substituting this value of u in (13.8.40b), we obtain

c =



γ − 1

γ +1



ξ +

γ +1

. (13.8.44)

It follows from c

= γkρ

γ−1

and (13.8.40b) with the initial data, ρ = ρ

c = c

that

ρ = ρ



γ − 1



2/(γ−1)

. (13.8.45)

With ξ =(x/t), results (13.8.43) through (13.8.45) give the complete

solution of the piston problem in terms of x and t.

Finally, the equation of the characteristic line Γ

is found by integrating

the second equation of (13.8.42) and using the boundary condition on the

piston. When a line Γ

intersects the piston path at time t = τ,then

u =

X (τ ) along it, and the equation becomes