Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

13.10 Structure of Shock Waves and Burgers’ Equation 571
Thus,
∞
−∞
x − ζ
t
exp
−
f
2ν
dζ =
0
−∞
x − ζ
t
exp
A
2ν
−
(x − ζ)
2
4νt
dζ
+
∞
0
x − ζ
t
exp
−
(x − ζ)
2
4νt
dζ
=2ν
e
A/2ν
− 1
exp
−
x
2
4νt
,
which is obtained by substitution,
x − ζ
2
√
νt
= α.
Similarly,
∞
−∞
exp
−
f
2ν
dζ =2
√
νt
√
π +
e
A/2ν
− 1
erfc
x
2
√
νt
,
where erfc (x) is the complementary error function defined by
erfc (x)=
2
√
π
∞
x
e
−η
2
dη. (13.10.31)
Therefore, the solution for u (x, t)is
u (x , t)=
ν
t
e
A/2ν
− 1
exp
−
x
2
4νt
√
π +
e
A/2ν
− 1
(
√
π/2) erf c
x
2
√
νt
. (13.10.32)
In the limit as ν →∞, the effect of diffusion would be more significant
than that of nonlinearity. Since
erfc
x
2
√
νt
→ 0,e
A/2ν
∼ 1+
A
2ν
as ν →∞,
the solution (13.10.32) tends to the limiting value
u (x , t) ∼
A
2
√
πν t
exp
−
x
2
4νt
. (13.10.33)
This represents the well-known source solution of th e classical linear heat
equation u
t
= νu
xx
.
On the other hand, when ν → 0 nonlinearity would dominate over
diffusion. It is expected that solution (13.10.32) tends to that of Burgers’
equation as ν → 0.
572 13 Nonlinear Partial Differential Equations with Applications
We next introduce the similarity vari able η = x/
√
2At to rewrite
(13.10.32) in the form
u (x , t)=
ν
t
1
2
e
A/2ν
− 1
exp
−
Aη
2
2ν
√
π +
e
A/2ν
− 1
(
√
π/2) erf c
%
A
2ν
η
, (13.10.34)
∼
ν
t
1
2
exp
&
A
2ν
1 − η
2
'
√
π +(
√
π/2) exp
A
2ν
erfc
%
A
2ν
η
as ν → 0 for all η,
(13.10.35)
∼ 0asν → 0, for η<0andη>1. (13.10.36)
Invoking the asymptotic result,
erfc (x) ∼
2/
√
π
e
−x
2
2x
as x →∞, (13.10.37)
the solution (13.10.34) for 0 <η<1 has the form,
u (x , t) ∼
ν
t
1
2
2η
A
2ν
1
2
exp
&
A
2ν
1 − η
2
'
2η
Aπ
2ν
1
2
+exp
&
A
2ν
(1 − η
2
)
'
.
=
2A
t
1
2
η
1+2η
Aπ
2ν
1
2
exp
&
A
2ν
(η
2
− 1)
'
∼
2A
t
1
2
as ν → 0.
The final asymptotic solution as ν → 0is
u (x , t) ∼
⎧
⎨
⎩
x
t
, 0 <x<(2At)
1
2
0, otherwise .
(13.10.38)
This result represents a shock at x =(2At)
1
2
with the velocity U =(A/2t)
1
2
.
This solution u has a jump from 0 to x/t =(2A/t)
1
2
so that the shock
condition is fulfilled.
Asymptotic Behavior of Burgers’ Solution as ν → 0.
We use the Kelvin stationary ph ase approximation method discussed in
Section 12.7 to examine the asymptotic behavior of Burgers’ solution
(13.10.30). According to this method, the significant contribution to the
integrals involved in (13.10.30) comes from points of stationary phase for
fixed x and t, that is, from the roots of the equation
13.11 The Korteweg–de Vries Equation and Solitons 573
∂f
∂ζ
= F (ζ) −
(x − ζ)
t
=0. (13.10.39)
Suppose that ζ = ξ (x, t) is a root. According to result (12.7.8), integrals
in (13.10.30) as ν → 0 yield
∞
−∞
x − ξ
t
exp
−
f
2ν
dζ ∼
x − ξ
t
4πν
|f
′′
(ξ)|
1
2
exp
−
f (ξ)
2ν
∞
−∞
exp
−
f
2ν
dζ ∼
4πν
|f
′′
(ξ)|
1
2
exp
−
f (ξ)
2ν
.
Therefore, the final asymptotic solution is
u (x , t) ∼
x − ξ
t
, (13.10.40)
where ξ satisfies (13.10.39). In other words, the solution can be rewritten
in the form
u
x
=
=
F (ξ)
ξ + tF (ξ)
. (13.10.41)
This is identical with the solution (13.2.12) which was obtained in Sec-
tion 13.2. In this case, the stationary point ξ represents the characteristic
variable.
Although the exact solution of Burgers’ equation is a single-valued an d
continuous function for all time t, the asymptotic solution (13.10.41) ex-
hibits instability. It has already been shown that (13.10.41) progressively
distorts itself and becomes multiple-valued after sufficiently long time.
Eventually, breaking will definitely occur.
It follows from the analysis of Burgers’ equation that the nonlinear and
diffusion terms show opposite effects. The former introduces steepening in
the solution profile, whereas the latter tends to diffuse (spread) the sharp
discontinuities into a smooth pr ofile. In view of this property, the solution
represents the diffusive wave. In the context of fluid flows, ν denotes the
kinematic viscosity which measures the viscous dissipation.
Finally, Burgers’ equation arises in many physical problems, includ-
ing one-dimensional turbulence (where this equation had its origin), sound
waves in viscous media, shock waves in viscous media, waves in fluid-filled
viscous elastic pipes, and magnetohydrodynamic waves in media with finite
conductivity.
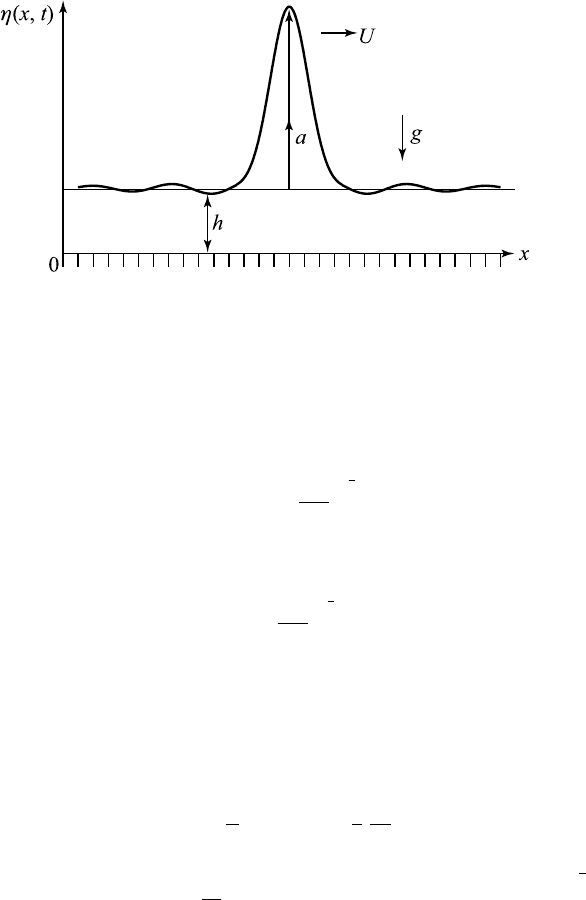
13.11 The Korteweg–de Vries Equation and Solitons
The celebrated dispersion relation (13.3.14) for dispersive surface waves on
water of constant depth h
0
is

574 13 Nonlinear Partial Differential Equations with Applications
ω =(gk tanh kh
0
)
1
2
= c
0
k
1 −
1
3
k
2
h
2
0
1
2
≈ c
0
k
1 −
1
6
k
2
h
2
0
, (13.11.1)
where c
0
=(gh
0
)
1
2
is the shallow water wave speed.
In many physical p rob lems, wave motions with small dispersion exhibit
such a k
2
term in contrast to the linearized theory value of c
0
k. An equation
for the fr ee surface elevation η (x, t) with this disp ersion relation is given
by
η
t
+ c
0
η
x
+ ση
xxx
=0, (13.11.2)
where σ =
1
6
c
0
h
2
0
is a constant f or fairly long waves. This equation is called
the linearized Korteweg–de Vries (KdV) equation for fairly long waves mov-
ingtothepositivex direction only. The phase and group velocities of the
waves are found from (13.11.1) and they are given by
C
p
=
ω
k
= c
0
− σk
2
, (13.11.3)
C
g
=
dω
dk
= c
0
− 3σk
2
. (13.11.4)
It is noted that C
p
>C
g
, and the dispersion comes from the term involving
k
3
in the dispersion relation (13.11.1) and hence, from the term ση
xxx
.For
sufficiently long waves (k → 0), C
p
= C
g
= c
0
, and hence, these waves are
nondispersive.
In 1895, K orteweg–de Vries derived the nonlinear equation for long wa-
ter waves in a channel of depth h
0
which has the remarkable form
η
t
+ c
0
1+
3
2
η
h
0
η
x
+ ση
xxx
=0. (13.11.5)
This is th e simplest nonlinear model equation for dispersive waves, and
combines nonlinearity and dispersion. The KdV equation arises in many
physical problems, which include water waves of long wavelengths, plasma
waves, and magnetohydynamics waves. Like Burgers’ equation, the nonlin-
earity and dispersion have opposite effects on the KdV equation. The former
introduces steepening of the wave profile while the latter counteracts wave-
form steepening. The most remarkable features is that the dispersive term
in the KdV equation does allow the solitary and periodic waves which are
not found in shallow water wave theory. In Burgers’ equation the nonlinear
term leads to steepening which produces a shock wave; on the other hand,
in the KdV equation the steepening process is balanced by dispersion to
give a rise to a steady solitary wave.
We now seek the traveling wave solution of the KdV equation (13.11.5)
in the form

13.11 The Korteweg–de Vries Equation and Solitons 575
η (x, t)=h
0
f (X) ,X= x − Ut, (13.11.6)
for some function f and constant wave velo city U . We determine f and
U by substitution of the form (13.11.6) into (13.11.5). This gives, with
σ =
1
6
c
0
h
2
0
,
1
6
h
2
0
f
′′′
+
3
2
ff
′
+
1 −
U
c
0
f
′
=0, (13.11.7)
and then integration leads to
1
6
h
2
0
f
′′
+
3
4
f
2
+
1 −
U
c
0
f + A =0,
where A is an integrating constant.
We next multiply this equation by f
′
and integrate again to obtain
1
3
h
2
0
f
′2
+ f
3
+2
1 −
U
c
0
f
2
+4Af + B =0, (13.11.8)
where B is a constant of integration.
We now seek a solitary wave solution under the boundary conditions f,
f
′
, f
′′
→ 0as|X|→∞. Therefore, A = B = 0 and (13.11.8) assumes the
form
1
3
h
2
0
f
′2
+ f
2
(f −α)=0, (13.11.9)
where
α =2
U
c
0
− 1
. (13.11.10)
Finally, we obtain
X =
f
0
df
f
′
=
h
2
0
3
1
2
f
0
df
f
(α − f)
,
which is, by the substitution f = α sech
2
θ,
X − X
0
=
4h
2
0
3α
1
2
θ, (13.11.11)
for some integrating constant X
0
.
Therefore, the solution for f (X)is
f (X)=α sech
2
3α
4h
2
0
1
2
(X − X
0
)
. (13.11.12)
576 13 Nonlinear Partial Differential Equations with Applications
Figure 13.11.1 A soliton.
The solution f (X) increases from f =0asX →−∞so that it attains a
maximum value f = f
max
= α at X = 0, and then decreases symmetrically
to f =0asX →∞as shown in Figure 13.11.1. These features also imply
that X
0
= 0, so that (13.11.12) becomes
f (X)=α sech
2
3α
4h
2
0
1
2
X
. (13.11.13)
Therefore, the final solution is
η (x, t)=η
0
sech
2
3η
0
4h
3
0
1
2
(x − Ut)
, (13.11.14)
where η
0
=(αh
0
). This is called the solitary wave solution of the KdV
equation for any positive constant η
0
. However, it has come to be known as
soliton since Zabusky and Kruskal coined the term in 1965. Since η>0for
all X, the soliton is a wave of elevation which is symmetrical about X =0.
It propagates in the medium without change of shape with velocity
U = c
0
1+
α
2
= c
0
1+
1
2
η
0
h
0
, (13.11.15)
which is directly proportional to the amplitude η
0
. The width,
3η
0
/4h
3
0
−
1
2
is inversely proportional to
√
η
0
. In other words, the solitary wave propa-
gates to the right with a velocity U which is directly proportional to the
amplitude, and has a width that is inversely proportional to the square root
of the amplitude. Therefore, taller solitons travel faster and are narrower
than the shorter (or slower) ones. They can overtake the shorter ones, and
surprisingly, they emerge from the interaction without change of shape as
shown in Figure 13.11.2. Indeed the discovery of soliton interactions con-
firms that solitons behave like elementary particles.
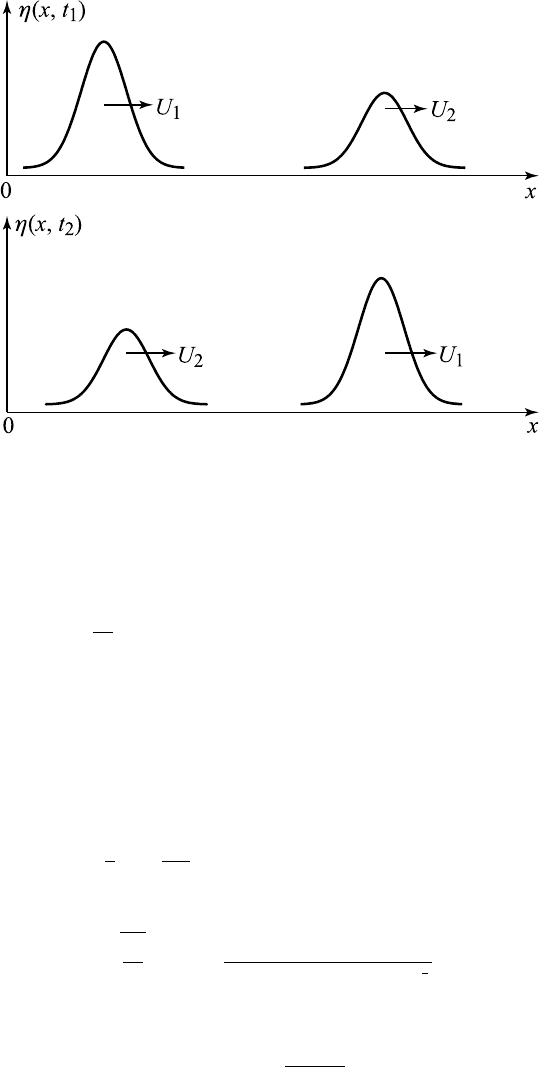
13.11 The Korteweg–de Vries Equation and Solitons 577
Figure 13.11.2 Interaction of two solitons (U
1
>U
2
,t
2
>t
1
, ).
General Waves of Permanent Form.
We now consider the general case given by (13.11.8) which can be written
h
2
0
3
f
′2
= −f
3
+ αf
2
− 4Af − B ≡ F (f) .
We seek real bounded solutions for f (X). Therefor e, f
′2
≥ 0andvaries
monotonically until f
′
is zero. Hence, the zeros of the cubic F (f ) are crucial.
For bounded solutions, all the three zeros f
1
, f
2
, f
3
must be real. Without
loss of generality, we choose f
1
= 0 and f
2
= α . The third zero must be
negative so we set f
3
= α − β with 0 <α<β. Therefore, the equation for
f (X)is
1
3
h
2
0
df
dX
2
= f (α − f )(f − α + β) , (13.11.16)
or
$
3
h
2
0
dX = −
df
[f (α − f )(f − α + β)]
1
2
, (13.11.17)
where
U = c
0
1+
2α − β
2
. (13.11.18)

578 13 Nonlinear Partial Differential Equations with Applications
We p ut α − f = p
2
in (13.11.17) to obtain
3
4h
2
0
1
2
dX =
dp
[(α − p
2
)(β − p
2
)]
1
2
. (13.11.19)
We next substitute p =
√
αq into (13.11.19) to transform it into the
standard form
3β
4h
2
0
1
2
X =
q
0
dq
[(1 − q
2
)(1− m
2
q
2
)]
1
2
(13.11.20)
where m =(α/β)
1
2
.
The right hand side is an integral of the first kind, and hence, q can
be expressed in terms of the Jacobi an sn function (see Dutta and Debnath
(1965))
q = sn
3β
4h
2
0
1
2
X, m
, (13.11.21)
where m is the modulus of the Jacobian elliptic function sn (z, m). There-
fore,
f (X)=α
1 − sn
2
/
3β
4h
2
0
1
2
X
0
= αcn
2
3β
4h
2
0
1
2
X
, (13.11.22)
where cn (z, m) is also the Jacobian elliptic function of modulus m and
cn
2
(z)=1− sn
2
(z).
From (13.11.20), the period P is given by
P =2
4h
2
0
3β
1
2
1
0
dq
[(1 − q
2
)(1− m
2
q
2
)]
1
2
(13.11.23)
=
4h
0
√
3β
K (m) ≡ λ, (13.11.24)
where K (m) is the complete elliptic integral of the first kind defined by
K (m)=
π/2
0
1 − m sin
2
θ
−
1
2
dθ (13.11.25)
and λ denotes the wavelength of the cnoidal wave.
It is important to note that cn (z, m) is periodic, and hence, η (X)rep-
resents a train of periodic waves in shallow water. Thus, th ese waves are
called cnoidal waves with wavelength
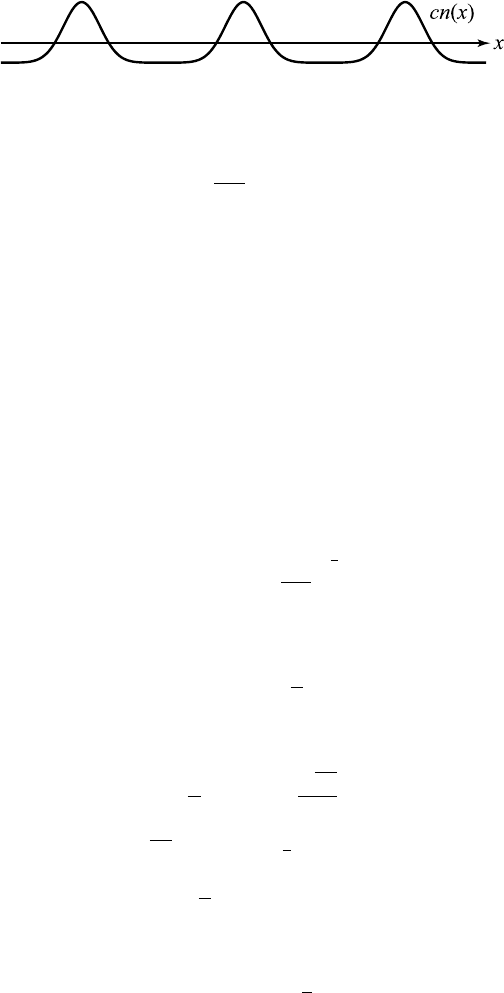
13.11 The Korteweg–de Vries Equation and Solitons 579
Figure 13.11.3 A cnoidal wave.
λ =2
4h
3
3b
1/2
K (m) . (13.11.26)
The outcome of this analysis is that solution (13. 11.22) represents a
nonlinear wave whose shape and wavelength (or period) all depend on the
amplitude of the wave. A typical cnoidal wave is shown in Figure 13.11.3.
Sometimes, the cnoidal waves with slowly varying amplitude are observed
in rivers. More often, wavetrains behind a weak bore (called an undular
bore ) can be regarded as cnoidal waves.
Two limiting cases are of special interest: (i) m → 1 and (ii) m → 0.
When m → 1(α → β), it is easy to show that cn (z) → sech z. Hence, the
cnoidal wave solution (13.11.22) tends to the solitary wave with the wave-
length λ, given by (13.11.24) which approaches infinity because K (1) = ∞,
K (0) = π/2. The solution i dentically reduces to (13.11.14) with (13.11.15).
In the other limit m → 0(α → 0), sn z → sin z an d cn z → cos z so that
solution (13.11.22) becomes
f (X)=α cos
2
3β
4h
2
0
1
2
X
, (13.11.27)
where
U = c
0
1 −
β
2
. (13.11.28)
Using cos 2θ =2cos
2
θ − 1, we can rewrite (13.11.27) in the form
f (X)=
α
2
1+cos
√
3β
h
0
X
. (13.11.29)
We next introduce k =
√
3β/h
0
(or β =
1
3
k
2
h
2
0
) to simplify (13.11.29) as
f (X)=
α
2
[1 + cos (kx − ωt)] , (13.11.30)
where
ω = Uk = c
0
k
1 −
1
6
k
2
h
2
0
. (13.11.31)
This corresponds to the first two terms of the series of (gk tanh kh
0
)
1/2
.
Thus, these results are in perfect agreement with the linearized theory.

580 13 Nonlinear Partial Differential Equations with Applications
Remark: It is important to point out that the phase velocity (13.11.3)
becomes negative for k
2
> (c
0
/σ) which indicates that waves propagate
in the negative x direction. This contradicts the original assumption of
forward travelling waves. Moreover, th e group velocity given by (13.11.4)
assumes large negative values for large k so that the fine-scale features of
the solution are propagated in the negative x direction. The solution of
(13.11.2) involves the Airy function which shows fiercely oscillatory char-
acter for large negative arguments. This leads to a lack of continuity and a
tendency to emphasize short wave components which contradicts the KdV
model representing fairly long waves. In order to eliminate these physically
undesirable features of the KdV equation, Benjamin, Bona, and Mahony
(1972) proposed a new nonlinear model equation in the form
η
t
+ η
x
+ ηη
x
− η
xxt
=0. (13.11.32)
This is known as the Benjamin, Bona and Mahony (BBM) equation.The
advantage of this model over the KdV equation becomes apparent when
we examine their linearized forms and the corresponding solutions. The
linearized form (13.11.32) gives the dispersion relation
ω =
k
1+k
2
, (13.11.33)
which shows that both the phase velocity and the group velocity are
bounded f or all k, and both velocities tend to zero for large k. In other
words, the model has the desirable feature of responding very insignifi-
cantly to short wave components that may be introduced into the initial
wave form. Thus, the BBM model seems to be a preferable long wave model
of physical interest. However, whether the BBM equation is a better model
than the KdV equation has not yet been established.
Another important property of the KdV equation is that it satisfies the
conservation law of the form
T
t
+ X
x
=0, (13. 11.34)
where T is called the density and the X is called the flux.
If T and X areintegrablein−∞ <x<∞,andX → 0as|x|→∞,
then
d
dt
∞
−∞
Tdx= −|X|
∞
−∞
=0.
Therefore,
∞
−∞
Tdx= constant
so that the density is conserved.
