Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

Numerical and Approximation Methods

“The strides that have been made recently, in the theory of nonlinear partial

diﬀerential equations, are as great as in the linear theory. Unlike the linear

case, no wholesale liquidation of broad classes of problems has taken place;

rather, it is steady progress on old fronts and on some new ones, the com-

plete solution of some special problems, and the discovery of some brand

new phenomena. The old tools – variation al methods, ﬁxed point theorems,

mapping degree, and other topological tools have been augmented by some

new ones. Pre-eminent for discovering new phenomena is numerical exper-

imentation; but it is likely that in the future numerical calculations will be

parts of proofs.”

Peter Lax

“Almost everyone using computers has experienced instances where

computational results have sparked new insights.”

Norman J. Zabusky

14.1 Introduction

The p r eceding chapters have been devoted to the analytical treatment of

linear and nonlinear partial diﬀerential equations. Several analytical meth-

ods to ﬁnd the exact analytical solution of these equations within simple

domains have been discussed. The boundary and initial conditi ons in these

problems were also relatively simple, and were expressible in simple math-

ematical form. In dealing with many equations arising from the modelling

of physical problems, the determination of such exact solutions in a simple

domain is a formidable task even when the boundary and/or initial data are

simple. It is then necessary to resort to numerical or appr oximation meth-

ods in order to deal with the problems that cannot be solved analytically. In

602 14 Numerical and Approximation Methods

view of the widespread accessibility of today’s high speed electronic com-

puters, numerical and appr oximation methods are becoming increasingly

important and useful in applications.

In this chapter some of the major numerical and approximation ap-

proaches to the solution of partial diﬀerential equations are d iscussed in

some detail. These include numerical methods based on ﬁnite diﬀerence ap-

proximations, variational methods, and the Rayleigh–Ritz, Galerkin, and

Kantorovich methods of approximation. The chapter also contains a large

section on analytical treatment of variational methods and the Euler–

Lagrange equations and their applications. A short section on the ﬁnite

element method is also included.

14.2 Finite Diﬀerence Approximations, Convergence,

and Stability

The Taylor series expansion of a function u (x, y) of two independent vari-

ables x and y is

u (x

h, y

)=u

i +

1,j

= u

i,j

h (u

)

i,j

)

i,j

xxx

)

i,j

+ ..., (14.2.1ab )

u (x

k)=u

i,j +

= u

i,j

k (u

)

i,j

)

i,j

yyy

)

i,j

+ ..., (14.2.2ab)

where u

i,j

= u (x, y), u

i +

1,j

= u (x +

h, y), and u

i,j +

= u (x, y +

k).

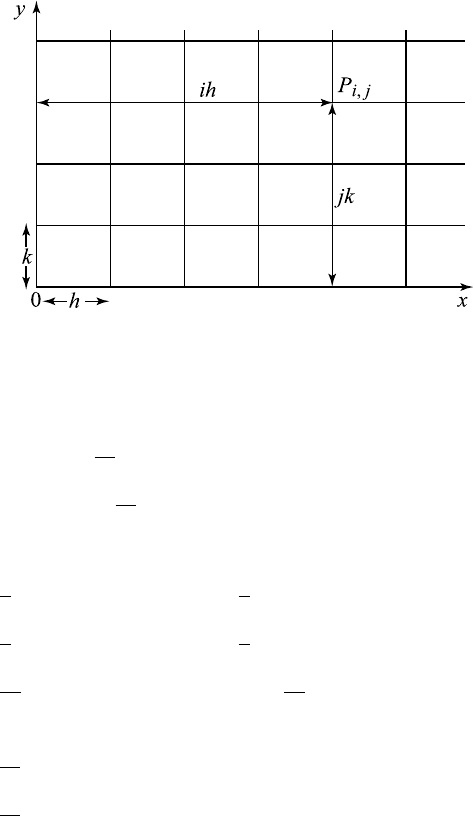
We choose a set of uniformly spaced rectangles with vertices at P

i,j

with

coordinates (ih, jk), where i, j, are positive or negative integers or zero, as

shown in Figure 14.2.1. We denote u (ih, jk)byu

i,j

Using the above Taylor series expansion, we write approximate expres-

sions for u

at the vertex P

i,j

in terms of u

i,j

, u

i +

1,j

[u (x + h, y) − u (x, y)] ∼

i+1,j

− u

i,j

)+O (h) , (14.2.3)

[u (x, y) − u (x − h, y)] ∼

i,j

− u

i−1,j

)+O (h) , (14.2.4)

[u (x + h, y) − u (x − h, y)] ∼

i+1,j

− u

i−1,j

)+O





(14.2.5)

These expressions are called the forward ﬁrst diﬀerence, backward ﬁrst

diﬀerence,andcentral ﬁrst diﬀerence of u

, respectively. The quantity O (h)

or O





is known as the truncation error in this discretization process.

14.2 Finite Diﬀerence Approximations, Convergence, and Stability 603

Figure 14.2.1 Uniformly spaced rectangles.

A similar approximate result for u

at the vertex P

i,j

[u (x + h, y) − 2 u (x, y)+u (x − h, y)]

∼

i+1,j

− 2 u

i,j

+ u

i−1,j

]+O





. (14.2.6)

Similarly, the approximate formulas for u

and u

at P

i,j

are

[u (x, y + k) − u (x, y)] ∼

i,j+1

− u

i,j

)+O (k) , (14.2.7)

[u (x, y) − u (x, y − k)] ∼

i,j

− u

i,j−1

)+O (k) , (14.2.8)

[u (x, y + k) − u (x, y − k)] ∼

i,j+1

− u

i,j−1

)+O





(14.2.9)

[u (x, y + k) − 2 u (x, y)+u (x, y − k)]

∼

i,j+1

− 2u

i,j

+ u

i,j−1

]+O





. (14.2.10)

All these diﬀerence formulas are extremely useful in ﬁnding numerical

solutions of ﬁrst or second order partial diﬀerential equations.

Suppose U (x, y) represents the exact solution of a partial diﬀerential

equation L (U) = 0 with independent variables x an d y,andu

i,j

is the

exact solution of the corresponding ﬁnite diﬀerence equation F (u

i,j

)=0.

Then, the ﬁnite diﬀerence scheme is said to be convergent if u

i,j

tends to

U as h and k tend to zero. The diﬀerence, d

i,j

≡ (U

i,j

− u

i,j

) is called the

cummulative truncation (or discretization) error.

This error can generally be minimized by decreasing the grid sizes h

and k. However, this error depends not only on h and k, but also on the

604 14 Numerical and Approximation Methods

number of terms in the truncated series which is used to approximate each

partial derivative.

Another kind of error is introduced when a parti al diﬀerential equation

is ap proximated by a ﬁnite diﬀerence equation. If the exact ﬁnite diﬀerence

solution u

i,j

is replaced by the exact solution U

i,j

of the par tial diﬀerential

equation at the grid points P

i,j

, then the value F (U

i,j

) is called the local

truncation error at P

i,j

. The ﬁnite diﬀerence scheme and the partial diﬀer-

ential equation are said to be consistent if F (U

i,j

) tends to zero as h and

k tend to zero.

In general, ﬁnite diﬀerence equations cannot be solved exactly because

the numerical computation is carried out only up to a ﬁnite number of

decimal places. Consequently, another kind of error is introduced in the

ﬁnite diﬀerence solution duri ng the actual process of computation. This

kind of error is called the round-oﬀ error, and it also depends upon the

type of computer used. In practice, the actual computation al solution is

∗

i,j

, but not u

i,j

, so that the diﬀerence r

i,j



i,j

− u

∗

i,j



is the round-

oﬀ error at the grid point P

i,j

. In fact, this error is introduced into the

solution of the ﬁnite diﬀerence equation by round-oﬀ errors. In reality, the

round-oﬀ error depends mainly on the actual computational process and

the ﬁnite diﬀerence itself. In contrast to the cummulative truncation error,

the round-oﬀ error cannot be made small by allowing h and k to tend to

zero.

Thus, the total error involved in the ﬁnite diﬀerence analysis at the

point P

i,j

is given by



i,j

− u

∗

i,j



=(U

i,j

− u

i,j



i,j

− u

∗

i,j



= d

i,j

− r

i,j

. (14.2.11)

Usually the discretization error d

i,j

is bounded when u

i,j

is bounded

because the value of U

i,j

is ﬁxed for a given partial diﬀerential equation

with the prescribed boundary and initial data. This fact is used or assumed

in order to introduce the concept of stability. The ﬁnite diﬀerence algo-

rithm is said to be stable if the round-oﬀ errors are suﬃciently small for

all i as j →∞, that is, the growth of r

i,j

can be controlled. It should be

pointed out again that the round-oﬀ error depends not only on the actual

computational process and the type of computer used, but also on the ﬁnite

diﬀerence equation itself. Lax (1954) proved a remarkable theorem which

establishes the relationship between consistency, stability, and convergence

for the ﬁnite diﬀerence algorithm.

Theorem 14.2.1. (Lax’s Equivalence Theorem). Given a properly posed

linear initial-value problem and a ﬁnite diﬀerence approxi mation to it that

satisﬁes the consistency criterion, stability is a necessary and suﬃcient

condition for convergence.

14.3 Lax–Wendroﬀ Explicit Method 605

Von Neumann’s Stability Method

This method is essentially based u pon a ﬁnite Fourier series. It expresses

the initial errors on the line t = 0 in terms of a ﬁnite Fourier series and then

examines the propagation of errors as t →∞. It is convenient to denote

the error fu nction by e

r,s

instead of e

i,j

so that e

r,s

gives the initial values

r,0

= e (rh)=e

on the line t = 0 between x = 0 and x = l,wherer =0,

1, 2, ..., N and Nh = l. The ﬁnite Fourier series expansion of e



n=0

exp (inπx/l)=



n=0

exp (iα

rh) , (14.2.12)

where α

=(nπ/l), x = rh,andA

are the Fourier coeﬃcients which are

determined from the (N + 1) equations (14.2.12).

Since we are concerned with the linear ﬁnite diﬀerence scheme, errors

form an additi ve system so that the total error can b e found by the superp o-

sition principle. Thus, it is suﬃcient t o consider a single term exp (iαrh)in

the Fourier series (14.2.12). Following the method of separation of variables

commonly used for ﬁnding the analytical solu tion of a partial diﬀerential

equation, we seek a separable solution of the ﬁni te diﬀerence equation for

r,s

in the form

r,s

=exp(iαrh + βsk)=exp(iαrh) p

(14.2.13)

which reduces to exp (iαrh)ats =0(t = sk = 0), where p =exp(βk), and

β is a complex constant. This shows that the error is bounded as (t →∞)

provided that

|p|≤1 (14.2.14)

is satisﬁed. This condition is found to be necessary and suﬃcient for the

stability of the ﬁnite diﬀerence algorithm.

14.3 Lax–Wendroﬀ Explicit Method

To describe this method, we consider the ﬁrst-order conservation equation

∂u

∂t

+ c

∂u

∂x

= 0 (14.3.1)

where u ≡ u (x, t) is some physical function of space variable x and time t.

This equation occurs frequently in applied mathematics.

Lax and Wendroﬀ use the Taylor series expansion in t in the form

i,j+1

= u

i,j

+ k (u

)

i,j

)

i,j

ttt

)

i,j

+ ..., (14.3.2)

606 14 Numerical and Approximation Methods

where k ≡ δt.

The partial derivatives in t in (14.3.2) can easily be eliminated by using

= −cu

so that (14.3.2) becomes

i,j+1

= u

i,j

− ck(u

)

i,j

)

i,j

− .... (14.3.3)

Replacing u

, u

by the central diﬀerence formulas, (14.3.3) becomes

i,j+1

= u

i,j

−





i+1,j

− u

i−1,j





i+1,j

− 2 u

i,j

+ u

i−1,j

) ,

i,j+1



1 − ε



i,j

(1 + ε) u

i−1,j

−

(1 + ε) u

i+1,j

+ O





,(14.3.4)

where ε =(ck/h). This is called the Lax–Wendroﬀ second-order ﬁnite dif-

ference scheme; it has been widely used to solve ﬁrst-order hyperbolic equa-

tions.

Von Neumann criterion (14.2.14) can be applied to investigate the sta-

bility of the Lax–Wendroﬀ scheme. It is noted that the error function e

r,s

given by (14.2.13) satisﬁes the ﬁnite diﬀerence equation (14.3.4). We then

substitute (14.2.13) into (14.3.4) and cancel common factors to obtain

p =



1 − ε



(1 + ε) e

−iαh

− (1 − ε) e

iαh

=1− 2 ε

sin



αh



− 2iε sin



αh



cos



αh



so that

|p|

=1− 4ε



1 − ε



sin



αh



. (14.3.5)

According to the von Neumann criterion, the Lax–Wendroﬀ scheme

(14.3.4) is stable as t →∞if |p|≤1, which gives 4ε



1 − ε



≥ 0, that is,

0 <ε≤ 1.

The local truncation error of the Lax–Wendroﬀ equation (14.3.4) at P

i,j

i,j+1

− u

i−1,j

)

which is, by (14.2.2a) and (14.2.1b) with ck = h (ε = 1),

=(u

+ cu

)

i,j



− c

xxx



i,j



ttt

+ c

xxx



i,j

+ O



(ck)



(14.3.6)

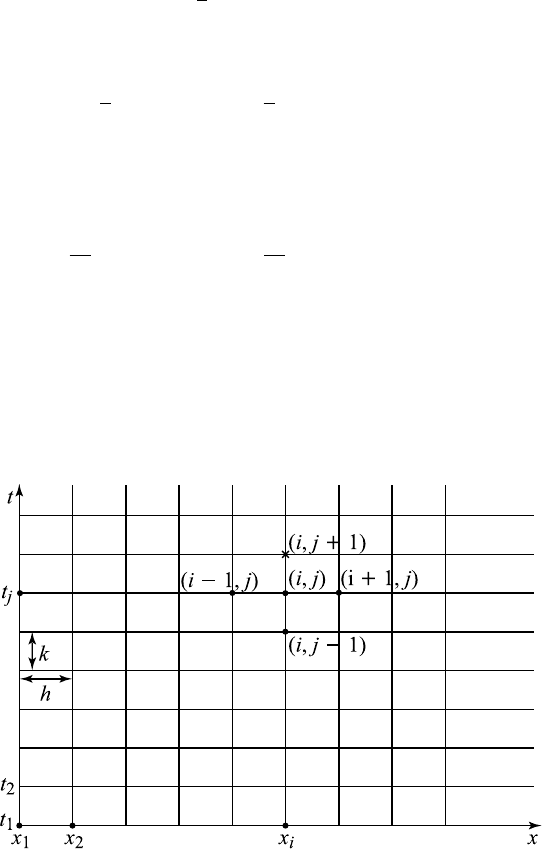
14.3 Lax–Wendroﬀ Explicit Method 607

The ﬁrst two terms on the right side of (14.3.6) vanish by equation (14.3.1)

so that the local truncation error becomes

i,j



ttt

+ ch

xxx



i,j

. (14.3.7)

Another approximation to (14.3.1) with ﬁrst-order accuracy is

i,j+1

− u

i,j

− u

i−1,j

)=0. (14.3.8)

A ﬁnal explicit scheme for (14.3.1) is based on the central diﬀerence ap-

proximation.Thisschemeiscalledtheleap frog algorithm. In this method,

the ﬁnite diﬀerence approximation to (14.3.1) is

i,j+1

− u

i,j−1

i+1,j

− u

i−1,j

)=0,

or,

i,j+1

= u

i,j−1

− ε (u

i+1,j

− u

i−1,j

) . (14.3.9)

As shown in Figure 14.3.1, this equation shows that the value of u at

i,j+1

is computed from the previously computed values at three grid points

at two previous time steps.

Figure 14.3.1 Grid system for the leap frog algorithm.

608 14 Numerical and Approximation Methods

14.4 Explicit Finite Diﬀerence Methods

(A) Wave Equation and the Courant–Friedrichs–Lewy

Convergence Criterion

The method of characteristics provides the most convenient and accurate

procedure for solving Cauchy problems involving hyperbolic equations. One

of the main advantages of this method is that discontinuities of the initial

data propagate into the solution domain along the characteristics. However,

when the initial data are discontinuous, the ﬁnite diﬀerence algorithm for

the hyperbolic systems is not very convenient. Problems concerning hyper-

bolic equations with continuous initial data can be solved successfully by

ﬁnite diﬀerence methods with rectangular gr id systems.

A commonly cited pr oblem is the propagation of a one-dimensional wave

governed by the system

= c

, −∞ <x<∞,t>0, (14.4.1)

u (x , 0) = f (x) ,u

(x, 0) = g (x) for all x ∈ R. (14.4.2)

Using a rectangular grid system with h = δx, k = δt, u

i,j

= u (ih, jk),

−∞ <x<∞,and0≤ j<∞, the central diﬀerence approximation to

equation (14.4.1) is

i,j+1

− 2 u

i,j

+ u

i,j−1

i+1,j

− 2 u

i,j

+ u

i−1,j

) ,

or,

i,j+1

= ε

i+1,j

+ u

i−1,j

)+2



1 − ε



i,j

− u

i,j−1

, (14.4.3)

where ε ≡ (ck/h), and is often called the Courant parameter. This explicit

formula allows us to determine the approximate values at the grid points

on the lines t =2k,3k,4k, ..., when the grid values at t = k have been

obtained.

The approximate values of the initial data on the line t = 0 are

i,0

= f

i,1

− u

i,−1

)=g

i,0

(14.4.4)

so that the second result gives

i,−1

= u

i,1

− 2kg

i,0

. (14.4.5)

When j = 0 in (14.4.3) and (14.4.5) is used, we obtain

i,1

i−1

+ f

i+1



1 − ε



+ kg

i,0

. (14.4.6)

This result determines grid values on the line t = k.

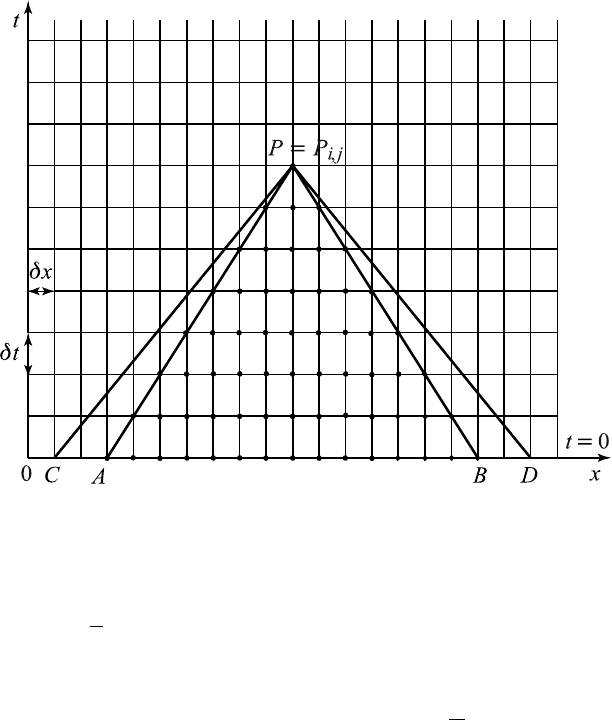
14.4 Explicit Finite Diﬀerence Methods 609

Figure 14.4.1 Computational grid systems and characteristics.

The value of u at P

i,j+1

is obtain ed in terms of its previously calculated

values at P

i +

1,j

, P

i,j

,andP

i,j−1

, which are determined from previously

computed values on th e lines t =(j − 1) k,(j − 2) k,(j − 3) k. Thus, the

computation from the lines t = 0 and t = k suggests that u at P

i,j

will rep-

resent a function of the values of u within the domain bounded by the lines

drawn back toward t =0fromP whose gradients are (+

ε) as shown in Fig-

ure 14.4.1. Thus the triangular regions PAB, PCD represent the domains

of dependence at P of the solutions of the ﬁnite diﬀerence equation (14.4.3)

and the diﬀerential equation (14.4.1). By analogy with real characteristic

lines PC and PD of the diﬀerential equation, the straight lines PA and

PB are called the numerical characteristi cs. Thus, it f ollows from Figure

14.4.1 that ∆P AB lies inside ∆P CD, which means that the soluti on of the

ﬁnite diﬀerence system at P would remain unchanged even when the initial

data along PA and PB are changed. Courant, Friedrichs and Lewy (CFL,

1928) proved that the solution of the ﬁnite diﬀerence system converges to

that of the diﬀerential equation system as h and k tend to zero provided

that the domain of dependence of the diﬀerence equation lies inside that of

the partial diﬀerential equation. This condition for convergence is known

as the CFL condition,whichmeans1/c ≥ k/h,thatis,0<ε≤ 1.

If the Courant parameter is ε = 1, equation (14.4.3) reduces to a simple

form

610 14 Numerical and Approximation Methods

i,j+1

= u

i+1,j

+ u

i−1,j

− u

i,j−1

. (14.4.7)

As shown in Figure 14.3.1, this equation shows that the value of u at

i,j+1

is computed from the previously computed values at three grid points

at two previous time steps. This is called the leap frog algorithm.

From equation (5.3.4) in Chapter 5, we know that the solution of the

Cauchy problem for the wave equation has the form

u (x , t)=φ (x + ct)+ψ (x − ct) ,

where the functions φ and ψ represent waves propagating without changing

shape along the negative and positive x directions with a constant speed

c. The lines of slope (dt/dx)=+

(1/c)inthex − t plane, which trace the

progress of the waves, are known as the characteristics of the wave equation.

In terms of a grid p oint (x

), the above solution has the form

i,j

= φ (x

+ ct

)+ψ (x

− ct

) . (14.4.8)

It follows from Figure 14.3.1 that x

= x

+(i − 1) h and t

= t

(j − 1) k so that (14.4.8) takes the f or m

i,j

= φ (α + ih + jck)+ψ (β + ih − jck) , (14.4.9)

where

α =(x

− h)+c (t

− k) ,β=(x

− h) − c (t

− k) .

Since ε =1,ck = h, solution (14.4.9) becomes

i,j

= φ (α +(i + j) h)+ψ (β +(i − j) h) .

This satisﬁes equation (14.4.7). It follows that the leap frog metho d

gives the exact solution of the partial diﬀerential equation (14.4.1).

We apply von Neumann stability analysis to investigate the stability of

the above numerical method for the wave equation. We seek a separable

solution of the error function e

r,s

=exp(iαrh) p

, (14.4.10)

where p =exp(βk). This function satisﬁes the ﬁnite diﬀerence equation

(14.4.3). Substituting (14.4.10) into (14.4.3) and cancelling the common

factors, we obtain th e quadratic equation for p

− 2 bp+1=0, (14.4.11)

where b =1− 2ε

sin

(αh/2), ε =(ck/h), and b ≤ 1 for all real ε and α.

This quadratic equation has two complex roots p

and p

if b

< 1. Since

·p

= 1, it follows that on e of the roots will always have modulus greater