Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

14.4 Explicit Finite Diﬀerence Methods 621

or,

i,j

i+1,j

+ u

i−1,j

+ u

i,j+1

+ u

i,j−1

i,j

where f

i,j

= f (i h, jh). This is known as the ﬁve-point formula.

Example 14.4.7. Find the numerical solution of the torsion problem in a

square beam governed by

∇

u = −2inD = {(x, y):0≤ x ≤ 1, 0 ≤ y ≤ 1}

with u (x, y)=0on∂D.

From the above ﬁve-point formula, we obtain

i,j

i+1,j

+ u

i−1,j

+ u

i,j+1

+ u

i,j−1

) −

where h is the side-length of the unit square net.

We choose h =

,1/2

to calculate the corresponding nu-

merical values u

i,j

=0.1250, 0.1401, 0.1456, 0.1469.

Note that the known exact analytical solution is 0.1474.

Example 14.4.8. Using the explicit ﬁnite diﬀerence method, ﬁnd the solu-

tion of the Dirichlet problem

+ u

=0, in 0 <x<1, 0 <y<1,

u (x , 0) = x , u (x, 1) = 0, on 0 ≤ x ≤ 1,

u (x , y)=0, for x =0,x=1 and 0≤ y ≤ 1.

We use four interior grid points (that is, i, j =1, 2, 3, 4) as shown in

Figure 14.4.2 in the (x, y)-plane.

We apply the explicit ﬁnite diﬀerence formula (14.4.32) to obtain four

algebraic equations

−4u

2,2

+ u

3,2

+ u

1,2

+ u

2,3

+ u

2,1

=0,

−4u

2,3

+ u

3,3

+ u

1,3

+ u

2,4

+ u

2,2

=0,

−4u

3,2

+ u

4,2

+ u

2,2

+ u

3,3

+ u

3,1

=0,

−4u

3,3

+ u

4,3

+ u

2,3

+ u

3,4

+ u

3,2

=0.

The given boundary conditions imply that u

2,1

= u

2,4

= u

3,1

= u

3,4

4,2

= u

4,3

=0,u

1,2

and u

1,3

so that the above system of equations

becomes

−4u

2,2

+ u

3,2

+ u

2,3

=0,

−4u

2,3

+ u

3,3

+ u

2,2

=0,

−4u

3,2

+ u

2,2

+ u

3,3

=0,

−4u

3,3

+ u

2,3

+ u

3,2

=0.

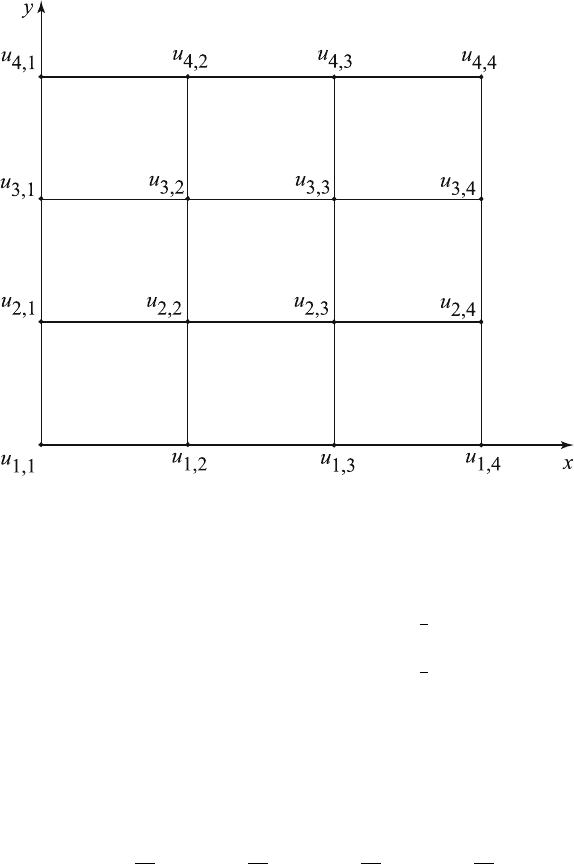
622 14 Numerical and Approximation Methods

Figure 14.4.2 The square grid system.

In matrix notation, this system reads as

⎡

⎢

⎣

−4110

1 −40 1

10−41

011−4

⎤

⎥

⎦

⎡

⎢

⎣

2,2

2,3

3,2

3,3

⎤

⎥

⎦

⎡

⎢

⎣

−

⎤

⎥

⎦

The solutions of this system are

2,2

2,3

3,2

3,3

(D) Simultaneous First-Order Equations

We recall the wave equation (14.4.1) in 0 <x<1, t>0. Introducing two

auxiliary variables v and w by v = u

and w = c

, the wave equation

gives two simultaneous ﬁrst-order equations

= w

= c

. (14.4.38)

14.4 Explicit Finite Diﬀerence Methods 623

The initial values of v and w are given at t =0forallx in 0 <x<1.

The boundary condition on v and w is also prescribed on the lines x =0

and x =1fort>0.

The explicit ﬁnite diﬀerence method can be used to determine v and

w in the triangular domain of dependence bounded by the characteristics

x − ct = 0 and x + ct =1.

The ﬁnite diﬀerence approximations to the diﬀerential equations (14.4.38)

are

i,j+1

− v

i,j

i+1,j

− w

i−1,j

) , (14.4.39)

i,j+1

− w

i,j

i+1,j

− v

i−1,j

) , (14.4.40)

where th e forward diﬀerence for v

or w

and the central diﬀerence for v

or w

are used. However, the central diﬀerence approximations to (14.4.38)

can also be utilized to obtain

i,j+1

− v

i,j−1

i+1,j

− w

i−1,j

) , (14.4.41)

i,j+1

− w

i,j−1

i+1,j

− v

i−1,j

) . (14.4.42)

We examine the stability of the above two sets of ﬁnite diﬀerence formu-

las with c = 1. The von Neumann stability method is applied by replacing

i and j by r and s respectively. The error function e

r,s

given by (14.4.10)

is substituted in (14.4.39)–(14.4.40) to obtain the stability relations

A (p − 1) = εiB sin αh, (14.4. 43)

B (p − 1) = εiA sin αh, (14.4.44)

where the initial perturbations in v and w along t = 0 are A exp (iαrh)and

B exp (iαrh) respectively with two diﬀerent constants A and B.

Elimination of A and B from the above relations gives

(p − 1)

+ ε

sin

αh =0

p =1+

iε sin αh,

and

|p| =



1+ε

sin

αh



∼ 1+

sin

αh =1+O





. (14.4.45)

Since |p| > 1+O (ε), the ﬁnite diﬀerence scheme for the ﬁnite time-step

t = sk would be unstable as the grid sizes tend to zero.

A similar stability analysis for (14.4.41)–(14.4.42) leads to the condition

624 14 Numerical and Approximation Methods



p −



+4ε

sin

αh =0. (14.4.46)

This scheme is stable for ε ≤ 1.

Another ﬁnite diﬀerence approximation to the coupl ed system (14.4.38)

r+1,s

− v

r−1,s



r,s+1

−

r+1,s

− w

r−1,s

)



, (14.4.47)

r+1,s

− w

r−1,s



r,s+1

−

r+1,s

− v

r−1,s

)



. (14.4.48)

A similar stability analysis can be carried out for these systems by

substituting v

r,s

= Ap

iαrh

and w

r,s

= Bp

iαrh

into the equations. Elim-

ination of A/B yields the stability equation

p =cosαh +

sin αh,

|p|

=cos

αh +

sin

αh ≤ 1. (14.4.49)

Hence, the scheme is stable provided that

ε ≥ 1, that is,k≤ h. (14.4.50)

14.5 Implicit Finite Diﬀerence Methods

From a computational point of view, the explicit ﬁnite diﬀerence algorithm

is simple and convenient. However, as shown in Section 14.4(B), the major

diﬃculty in the method for solving parabolic partial diﬀerential equations

is the severe restriction on the time-step imposed by the stability condi-

tion ε ≤

or k ≤ h

/2κ. This diﬃculty is also present in the explicit ﬁnite

diﬀerence method for the solution of hyperbolic equations. In order to over-

come the above diﬃculty, we d evelop implicit ﬁnite diﬀerence schemes for

solving partial diﬀerential equations.

(A) Parabolic Equations

One of the successful implicit ﬁnite diﬀerence schemes is the Crank and

Nicolson Method (1947), which is based on six grid points. This method

eliminates the major diﬃculty involved in the explicit scheme. When

the Crank–Nicolson implicit scheme is applied to the parabolic equation

(14.4.13), u

is replaced by the mean value of the ﬁnite diﬀerence values

14.5 Implicit Finite Diﬀerence Methods 625

in the jth and the (j + 1) th row so that the ﬁnite diﬀerence approximation

(14.4.13) becomes

i,j+1

− u

i,j

[(u

i+1,j+1

− 2u

i,j+1

+ u

i−1,j+1

)

+(u

i+1,j

− 2u

i,j

+ u

i−1,j

)] , (14.5.1)

2(1+ε) u

i,j+1

− ε (u

i−1,j+1

+ u

i+1,j+1

)

=2(1− ε) u

i,j

+ ε (u

i−1,j

+ u

i+1,j

) , (14.5.2)

where ε =



kκ/h



is a parameter.

The left side of (14.5.2) is a linear combination of three unknowns in

the (j + 1) th row, and the right side involves three known values of u in

the jth row of the grid system in the (x, t)-plane. Equation (14.5.2) is

called the Crank–Nicolson implicit formul a. This formula (or its suitable

modiﬁcation) is widely used for solving parabolic equations. If there are n

internal grid points along each jth row, then, for j = 0 and i =1,2,3,...,

n, the implicit formula (14.5.2) gives n simultaneous algebraic equations

for n unknown values of u along the ﬁrst jth row (j = 0) in terms of given

boundary and initial data. Similarly, if j = 1 and i =1,2,3,..., n, equation

(14.5.2) represents n unknown values of u along the second jth row (j =1)

and so on. This means that the method involves the solution of a system of

simultaneous algebraic equations. In practice, the Crank–Nicolson scheme

is convergent and unconditionally stable for all ﬁnite values of ε, and has

the advantage of reducing the amount of numerical computation.

This implicit scheme can b e further generalized by introducing a numer-

ical weight factor λ in the modiﬁed version of the explicit equation (14.4.16)

which is written below by approximating u

in (14.4.13) in the (j +1)th

row instead of the jth row.

i,j+1

− u

i,j

i+1,j+1

− 2u

i,j+1

+ u

i−1,j+1

) , (14.5.3)

i,j+1

− u

i,j

= ε (u

i+1,j+1

− 2u

i,j+1

+ u

i−1,j+1

) . (14.5.4)

Introducing the numerical factor λ, this can be replaced by a more

general diﬀerence equation in the form

i,j+1

− u

i,j

= ε

λδ

i,j+1

+(1− λ) δ

i,j

, (14.5.5)

where 0 ≤ λ ≤ 1andδ

is the diﬀerence operator deﬁned by

i,j

= u

i+1,j

− 2u

i,j

+ u

i−1,j

. (14.5.6)

Another equivalent form of (14.5.5) is

626 14 Numerical and Approximation Methods

(1 + 2ελ) u

i,j+1

− ελ (u

i+1,j+1

+ u

i−1,j+1

)

= {1 − 2ε (1 − λ)}u

i,j

+ ε (1 − λ)(u

i+1,j

− u

i−1,j

) . (14.5.7)

This is a fairly general implicit formula which reduces to (14.5.4) when

λ =1.Whenλ =

, (14.5.7) becomes the Crank–Nicolson formula (14.5.2).

Finally, if λ = 0, this implicit diﬀerence equation reduces to the explicit

equation (14.4.17).

The Richardson explicit scheme was found to be unconditionally unsta-

ble in Section 14.4. This undesirable feature of the scheme can be elimi-

nated by considering the corresponding implicit scheme. In terms of δ

,the

Richardson equation (14.4.22) can be expressed as

i,j+1

=2εδ

i,j

+ u

i,j−1

. (14.5.8)

To obtain the implicit Richardson formula, we replace δ

i,j

i,j+1

+ u

i,j

+ u

i,j−1

) in (14.5.8) and we obtain



1 −

2 ε



i,j+1

2ε

i,j



2ε



i,j−1

. (14.5.9)

This implicit scheme can be shown to be unconditionally stable. To

prove this result, we apply the von Neumann stability method with the

error function (14.5.9) to obtain the equation for p as

(1 + a) p

+ ap +(a − 1) = 0, (14.5.10)

where

a ≡



8ε



sin



αh



. (14.5.11)

The roots of the quadratic equation are

p =

−a +



4 − 3a



2(1+a)

. (14.5.12)

This gives |p|≤1 for all values of a. Hence, the result is proved.

Example 14.5.1. Obtain the numerical solution of the following p arabolic

system by using th e Crank–Nicolson method

= u

, 0 <x<1,t>0,

u (0,t)=u (1,t)=0,t≥ 0,

u (x , 0) = x (1 − x) , 0 ≤ x ≤ 1.

We recall the Crank–Nicolson equation (14.5.2) and then set h =0.2

and k =0.01 so that ε =

. The boundary and initial conditions give

14.5 Implicit Finite Diﬀerence Methods 627

0,0

= u

5,0

= u

0,1

= u

5,1

= 0 and u

i,0

= u (i h, 0) = ih (1 − ih), i =1,2,

3, 4. Consequently, formula (14.5.2) leads to the foll owing system of four

equations:

−u

0,1

− u

2,1

+10u

1,1

= u

0,0

+ u

2,0

+6u

1,0

−u

1,1

− u

3,1

+10u

2,1

= u

1,0

+ u

3,0

+6u

2,0

−u

2,1

− u

4,1

+10u

3,1

= u

2,0

+ u

4,0

+6u

3,0

−u

3,1

− u

5,1

+10u

4,1

= u

3,0

+ u

5,0

+6u

4,0

Using the boundary and initial conditions, the above system becomes

−u

2,1

+10u

1,1

=1.20

−u

1,1

+10u

2,1

− u

3,1

=1.84

−u

2,1

− u

4,1

+10u

3,1

=1.84

−u

3,1

+10u

4,1

=1.20.

These equations can be solved by direct elimination to obtain the solutions

as u

1,1

=0.1418, u

2,1

=0.2202, u

3,1

=0.2202, u

4,1

=0.1420.

(B) Hyperbolic Equations

We consider an implicit ﬁnite diﬀerence scheme to solve the initial boundary-

value problem consisting of the ﬁrst-order hyperbolic equation

∂u

∂t

+ c

∂u

∂x

=0, (c>0) , (14.5.13)

with the initial data u (x, 0) = U (x) and the boundar y condition u (0,t)=

V (t)where0≤ x, t<∞.

The implicit ﬁnite diﬀerence approximation to (14.5.13) is

i,j+1

− u

i,j

i,j+1

− u

i−1,j+1

)=0,

i,j

=(1+ε) u

i,j+1

− εu

i−1,j+1

, (14.5.14)

where ε =(ck/h).

The stability of the scheme can be examined by using the von Neumann

method with the error function (14.4.10). It turns out that

p =[1− ε + ε exp (−iαh)]

−1

, (14.5.15)

from which it follows that |p|≤1 for all h. Hence, the implicit scheme is

unconditionally stable.

628 14 Numerical and Approximation Methods

We next solve the wave equation u

= c

by an implicit ﬁnite diﬀer-

ence scheme. In this case, u

is replaced by the central diﬀerence formula,

and u

by the mean value of the central diﬀerence values in the (j − 1) th

and (j + 1) th rows. Consequently, the implicit diﬀerence approximation to

the wave equation is

i,j+1

− 2 u

i,j

+ u

i,j−1

[(u

i+1,j+1

− 2u

i,j+1

+ u

i−1,j+1

)

+(u

i+1,j−1

− 2 u

i,j−1

+ u

i−1,j−1

)] ,

(14.5.16)

where ε =(ck/h).

Expressing the solution for the (j +1)thstepintermsofthetwopre-

ceding steps gives



1+ε



i,j+1

− ε

i−1,j+1

+ u

i+1,j+1

)

=4u

i,j

+ ε

i−1,j−1

+ u

i+1,j−1

) − 2



1+ε



i,j−1

(14.5.17)

The N grid points along the time step, j =0,i =1,2,3,..., N,

(14.5.17) along with the ﬁnite diﬀerence approximation to the boundary

condition give N simultaneous equations for the N unknown values of u

along the ﬁrst time step. This constitutes a tridiagonal system of equations

that can be solved by direct or iterative numerical methods.

To investigate the stability of the imp licit scheme, we apply the von

Neumann stability method with the error function (14.4.10). This leads to

the equation

p +



1+2ε

sin

αh



−1

− 2bp +1=0, (14.5.18)

where b =



1+2ε

sin

αh/2



−1

so that 0 <b≤ 1.

Hence, the stability condition is

|p|≤1 (14.5.19)

which is always satisﬁed provided 0 <b≤ 1, that is, ε<1 for all positive

h. This conﬁrms the unconditional stability of the scheme.

A more general implicit scheme can be introduced by replacing u

the wave equation (14.4.1) with

∼



i,j+1

+ δ

i,j−1



+(1+2λ) δ

i,j

, (14.5.20)

14.6 Variational Methods and the Euler–Lagrange Equations 629

where λ is a numerical weight (relaxation) f actor and the central diﬀerence

operator δ

is given by (14.5.6). This general scheme allows us to approxi-

mate the wave equation with c = 1 by the form

i,j

= ε



i,j+1

+ δ

i,j−1



+(1− 2λ) δ

i,j

, (14.5.21)

where ε = k/h. This equation reduces to (14.5.16) when λ =

, and to the

explicit ﬁnite diﬀerence result when λ =0.

It follows from von Neumann stabi lity anal ysis that the implicit scheme

is unconditionally stable for λ ≥

. Von Neumann introduced another fairly

general ﬁnite diﬀerence algorithm for the wave equation (14.4.1) in the form

i,j

= ε

i,j

. (14.5.22)

This equation with appropriate boundary conditions can be solved by

the tridiagonal method. Von Neumann discussed the question of stability

of this implicit scheme and proved that the scheme is conditionally stable

if ω ≤

and unconditionally stable if ω>

14.6 Variational Methods and the Euler–Lagrange

Equations

To describe the variational methods and Rayleigh–Ritz appr oximate method,

it is convenient to introd uce the concepts of the inner product (pre-Hilbert)

and Hilbert spaces. An inner product space X consisting of elements u, v,

w, ... over the complex number ﬁeld C is a complex linear space with an

inner product u, v : X ×X → C such that

(i) u, v =

v, u, where the bar denotes the complex conjugate of v,u,

(ii) αu + βv,w = α u, w  + β v, w for any scalars α, β ∈ C,

(iii) u, u≥0; equality holds if and only if u =0.

By (i) u, u =

u, u,andsou, u is real. We denote u, u

= u,which

is called the norm of u. Thus, the norm is induced by the inner product.

Thus, every inner product space is a normed linear space under the norm

u =



u, u.

Let X be an inner product space. A sequence {u

} where u

∈ X for

every n is called a Cauchy sequence in X if and only if for every given ε>0

(no matter how small) we can ﬁnd an N (ε) such that

u

− u

 <ε for all n, m > N (ε) .

The space X is called complete if every Cauchy sequence converges to

apointinX. A complete normed linear space is called a Banach Space.A

complete linear inner product space is called a Hilbert Space and is usually

denoted by H.

630 14 Numerical and Approximation Methods

Example 14.6.1. Let C

be the set of all n-tuples of complex numbers. Thus,

is an n-dimensional Hilbert space with the inner product

x, y =



k=1

Obviously, the set of all n-tuples of real numbers R

is an n-dimensional

Hilbert space.

Example 14.6.2. Let l

be the set of all sequences with entries from C such

that

∞

k=1

< ∞. This forms a Hilbert space with the inner product

x, y =

∞



k=1

Example 14.6.3. Let L

([a, b]) be the set of all square integrable functions

in the Lebesgue sense in an interval [a, b]. L

([a, b]) is a Hilbert space with

the inner product

u, v =



u (x)

v (x) dx.

We next introduce the notion of an operator in a Hilbert space H.An

operator A is a mapping from H to H (that is, A : H → H). It assigns to

an element u in H a new element Au in H. An op erator A is called linear

if it satisﬁes the property

A (αu + βv)=αAu + βAv for every α, β ∈ C.

An operator is said to be bounded if there exists a constant k such that

Au≤k u for all u ∈ H.

We consider a b oun ded operator A on a Hilbert space H. For a ﬁxed

element v in H, the inner product Au, v in H can be regarded as a number

I (u)whichvarieswithu.Thus,Au, v = I (u)isalinear functional on H.

If there exists an operator A

∗

on a Hilbert space (A

∗

: H → H)such

that

Au, v = u, A

∗

v for all u, v ∈ H,

then A

∗

is called the adjoint of A. In general, A = A

∗

.IfA = A

∗

,thatis,

Au, v = u, Av for all u, v in H,thenA is called self-adjoint.

It is important to note that any bounded operator T on a real Hilbert

space (T : H → H) of the form T = A

∗

A is self-adjoint. This follows from

the fact that

Tu,v = A

∗

Au, v = Au, Av = u, A

∗

Au = u, T v.