Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

14.4 Explicit Finite Diﬀerence Methods 611

than one unless |p

| = |p

| = 1. Thus, the scheme is unstable as s →∞if

the modulus of one of the roots exceeds unity.

On the other hand, when −1 ≤ b ≤ 1, b

≤ 1, then |p

| = |p

| =1.

Thus, the ﬁnite diﬀerence scheme is stable provided −1 ≤ b ≤ 1, which

leads to the useful condition for stability as b ≥−1that

≤ cosec



αh



. (14.4.12)

This shows the dependence of the stability limit on the space-grid size h.

However, this stability condition is always true if ε

≤ 1.

Example 14.4.1. Find the explicit ﬁnite diﬀerence solution of the wave equa-

tion

− u

=0, 0 <x<1,t>0,

with the boundary conditions

u (0,t)=u (1,t)=0,t≥ 0,

and the initial conditions

u (x , 0) = sin πx, u

(x, 0) = 0, 0 ≤ x ≤ 1.

Compare the numerical solution with the analytical solution u (x, t)=

cos πt sin πx at several p oi nts.

The expli cit ﬁnite diﬀerence approximation to the wave equation with

ε =(k/h) = 1 is f oun d from (14.4.3) in the form

i,j+1

= u

i−1,j

+ u

i+1,j

− u

i,j−1

,j≥ 1.

The problem is symmetric with respect to x =

, so we need to calculate

the solution only for 0 ≤ x ≤

. We take h = k =

=0.1. The bound-

ary conditions give u

0,j

=0forj =0, 1, 2, 3, 4, 5. The initial condition

(x, 0) = 0 yields

(x, 0) =

i,1

− u

i,−1

)=0,

or,

i,1

= u

i,−1

The explicit formula with j = 0 gives

i,1

i−1,0

+ u

i+1,0

) ,i=1, 2, 3, 4, 5.

Thus,

612 14 Numerical and Approximation Methods

1,1

0,0

+ u

2,0

sin (0.2π)=0.2939.

Similarly,

2,1

=0.5590,u

3,1

=0.7695,u

4,1

=0.9045,u

5,1

=0.9511.

We next use the basic explicit formula to compute

1,2

= u

0,1

+ u

2,1

− u

1,0

=0+0.5590 − 0.3090 = 0.2500,

2,2

= u

1,1

+ u

3,1

− u

2,0

=0.2939 + 0.7695 − 0.5878 = 0.4756.

Similarly, we compute other values for u

i,j

which are shown in Table 14.4.1.

The analytical solu tions at (x, t)=(0.1, 0.1) and (0.2, 0.3) are given by

u (0.1, 0.1) = cos (0.1π)sin(0.1π)=(0.9511) (0.3090) = 0.2939,

u (0.2, 0.2) = cos (0.2π)sin(0.2π)=(0.8090) (0.5878) = 0.4577,

u (0.2, 0.3) = cos (0.3π)sin(0.2π)=(0.5878) (0.5878) = 0.3455.

Comparison of the analytical solutions with the above ﬁnite diﬀerence

solutions shows that the latter results are very accurate.

(B) Parabolic Equations

As a prototype diﬀusion problem, we consider

= κu

, 0 <x<1,t>0, (14.4.13)

u (0,t)=u (1,t)=0, for all t, (14.4.14)

u (x , 0) = f (x) , for all x in (0, 1) , (14.4.15)

where f (x) is a given f un ction.

Table 14.4.1.

i 0 1 2 3 4 5

x 0.0 0.1 0.2 0.3 0.4 0.5

10.1 0 0.2939 0.5590 0. 7695 0.9045 0.9511

20.2 0 0.2500 0.4577 0. 6545 0.7695 0.8090

30.3 0 0.1817 0.3455 0. 4756 0.5590 0.5878

40.4 0 0.9045 0.7695 0. 2500 0.2939 0.3090

50.5 0 0 0 0 0 0

14.4 Explicit Finite Diﬀerence Methods 613

The explicit ﬁnite diﬀerence approximation to (14.4.13) is

i,j+1

− u

i,j

i+1,j

− 2 u

i,j

+ u

i−1,j

) , (14.4.16)

or,

i,j+1

= ε (u

i+1,j

+ u

i−1,j

)+(1− 2 ε) u

i,j

, (14.4.17)

where ε =



κk/h



This explicit ﬁnite diﬀerence formula gives approximate values of u on

t =(j +1)k in terms of values on t = jk with given u

i,0

= f

.Thus,u

i,j

can be obtained for all j by successive use of (14.4.17).

The problems of stability and convergence of the parabolic equation are

similar to those of the wave equation. It can be shown that the solution of

the ﬁnite diﬀerence equation converges to that of the diﬀerential equation

system (14.4.13)–(14.4.15) as h and k tend to zero provided ε ≤

In particular, when ε =

, equation (14.4.17) takes a simple form

i,j+1

i+1,j

+ u

i−1,j

) . (14.4.18)

This is called the Bender–Schmidt explicit formula which determines the

solution at (x

j+1

) as the mean of the values at the grid points (i +

1,j).

However, more accurate results can be found from (14.4.17) for ε<

To investigate the stability of the numerical scheme, we assume that the

error function is

r,s

=exp(iαrh) p

, (14.4.19)

where p = e

βk

. The error function and u

satisfy the same diﬀerence

equation. Hence, we substitute (14.4.19) into (14.4.17) to obtain

p =1− 4 ε sin



αh



. (14.4.20)

Clearly, p is always less than 1 because ε>0. If p ≥ 0, the function given

by (14.4.19) will decay steadily as s = j →∞.If−1 <p<0, then the

solution will have a decaying amplitude as s →∞. Therefore, the ﬁnite

diﬀerence scheme will be stable if p>−1, that is, if

0 <ε≤

cosec



αh



. (14.4.21)

This shows that the stability limit depends on h. However, in view of the

inequality

ε ≤

≤

cosec



αh



we conclude that the stability condition is ε ≤

. Finally, if p<−1, the

solution oscillates with increasing amplitude as s →∞, and hence, the

scheme will be unstable for ε>

614 14 Numerical and Approximation Methods

Example 14.4.2. Show that the Richardson explicit ﬁnite diﬀerence scheme

for (14.4.13) is unconditionally unstable.

The Richardson ﬁnite d iﬀerence approximation to (14.4.13) is

i,j+1

− u

i,j−1

i+1,j

− 2 u

i,j

+ u

i−1,j

) . (14.4.22)

To establish the instability of this equation, we use the Fourier method

and assume that

r,s

=exp(iαrh) p

,p= e

βk

This function satisﬁes the Richardson diﬀerence equation as does u

r,s

. Con-

sequently,

p −

= −8 ε sin



αh



+8pεsin



αh



− 1=0.

This quadratic equation has two roots

= −4 ε sin



αh





1+16ε

sin

αh



, (14.4.23)

1 − 4 ε sin



αh



+2ε sin

αh



+ O





This gives |p

|≤1and

| > 1+4ε sin



αh



> 1

for all positive ε and, consequently, the Richardson scheme is always un-

stable.

The unstable feature of the Richardson scheme can be eliminated by

replacing u

i,j

with

i,j+1

+ u

i,j−1

) in (14.4.22), which now becomes

(1 + 2 ε) u

i,j+1

=2ε (u

i+1,j

+ u

i−1,j

)+(1− 2 ε) u

i,j−1

. (14.4.24)

This is called the Du Fort–Frankel explicit algorithm,anditcanbe

shown to be stable for all ε.

14.4 Explicit Finite Diﬀerence Methods 615

Example 14.4.3. Prove that the solution of the ﬁnite diﬀerence equation for

the diﬀusion equation (14.4.13) i n −∞ <x<∞ with the initial condition

u (x , 0) = e

iαx

converges to the exact solution of (14.4.13) as h and k tend

to zero.

We obtain the exact solution of (14.4.13) by seeking a separable form

u (x , t)=e

iαx

v (t) ,

where v (t) is a function of t alone which is to be determined.

Substituting this solution into (14.4.13) gives

+ κα

v =0

which admits solutions

v (t)=Ae

−κα

where A is an integrating constant. The initial condition v (0) = 1 gives

A = 1. Hence,

u (x , t)=exp



iαx − α

κt



. (14.4.25)

We now solve the corresponding ﬁnite diﬀerence equation (14.4.17) by

replacing i, j with r, s. We seek a separable solution of the diﬀerence

equation

r,s

= e

iαrh

with the initial condition

r,0

= e

iαrh

, so that v

=1.

Substituting this solution into the ﬁnite diﬀerence equation (14.4.7)

yields

s+1



1 − 4 ε sin

αh



=1,

so that the solution can b e obtained by a simple inspection as



1 − 4 ε sin

αh



, (14.4.26)

r,s

= e

iαrh



1 − 4ε sin

αh



, (14.4.27)

where ε =



κk/h



For small h,1− 4 ε sin

(αh/2) ∼ 1 − εα

so that 1 − εα

≈

exp



−εα



for small εα

= κα

k. Consequently, the ﬁnal solution

becomes

616 14 Numerical and Approximation Methods

r,s

∼ e

iαrh−κα

as h, k → 0. (14.4.28)

This is identical with the exact solution of the diﬀerential equation (14.4.13)

with rh = x and sk = t. This example shows that the ﬁnite diﬀerence

approximation is reasonably good.

Example 14.4.4. Calculate a ﬁnite diﬀerence solution of the initial boundary-

value problem

= u

, 0 <x<1,t>0,

with the boundary conditions

u (0,t)=u (1,t)=0,t≥ 0,

and the initial condition

u (x , 0) = x (1 − x) , 0 ≤ x ≤ 1.

Compare the numerical solution with the exact analytical solution at

x =0.04 and t =0.02.

The explicit ﬁnite diﬀerence approximation to the parabolic equation is

i,j+1

= εu

i−1,j

+(1− 2 ε) u

i,j

+ εu

i+1,j

where ε =



k/h



. This gives the unknown value u

i,j+1

at the (i, j +1)th

grid point in terms of given values of u along the jth time row.

We set h =

and k =

100

so that ε =



k/h



and the above

formula becomes

i,j+1

i−1,j

+2u

i,j

+ u

i+1,j

) .

With the notation u

i,0

= u (ih, 0), the initial condition gives

4,0

=0.16, and u

5,0

=0.

The boundary conditions yield u

0,j

= u (0,jk)=0andu

5,j

u (5h, jk)=u (1,jk)=0,forallj =0,1,2,....

Using these initial and boundary data, we calculate u

i,j

as follows:

1,1

0,0

+2u

1,0

+ u

2,0

)=0.14,u

1,2

0,1

+2u

1,1

+ u

2,1

)

=0.125,

2,1

1,0

+2u

2,0

+ u

3,0

)=0.22,u

2,2

1,1

+2u

2,1

+ u

3,1

)

=0.200,

3,1

2,0

+2u

3,0

+ u

4,0

)=0.22,u

3,2

2,1

+2u

3,1

+ u

4,1

)

=0.200,

4,1

3,0

+2u

4,0

+ u

5,0

)=0.14,u

4,2

3,1

+2u

4,1

+ u

5,1

)

=0.125,

14.4 Explicit Finite Diﬀerence Methods 617

1,3

0,2

+2u

1,2

+ u

2,2

)=0.1125,u

1,4

0,3

+2u

1,3

+ u

2,3

)

=0.1016,

2,3

1,2

+2u

2,2

+ u

3,2

)=0.1813,u

2,4

1,3

+2u

2,3

+ u

3,3

)

=0.1641,

3,3

2,2

+2u

3,2

+ u

4,2

)=0.1813,u

3,4

2,3

+2u

3,3

+ u

4,3

)

=0.1641,

4,3

3,2

+2u

4,2

+ u

5,2

)=0.1125,u

4,4

3,3

+2u

4,3

+ u

5,3

)

=0.1016.

The method of separation of variables gives the analytical solution of

the problem as

u (x , t)=

∞



n=0

(2n +1)

exp

−(2n +1)

sin (2n +1)πx.

This exact solution u (x, t)atx =0.4(i =2)andt =0.02 (j =2)gives

u ∼



exp



−0.02 π



sin (0.4) π +

exp



−0.18 π



sin (1.2) π



=0.2000.

The analytical solution is seen to be identical with the numerical value.

Example 14.4.5. Obtain the numerical solution of the initial boundary-

value problem

= κu

, 0 ≤ x ≤ 1,t>0,

u (0,t)=1,u(1,t)=0,t≥ 0,

u (x , 0) = 0, 0 ≤ x ≤ 1.

We use the explicit ﬁnite-diﬀerence formula (14.4.17)

i.j+1

= ε (u

i+1,j

+ u

i−1,j

)+(1− 2 ε) u

i,j

where ε =



κk/h



We set h =0.25 =

and ε =

=0.4tocomputeu

i.j

for i, j =0,1,2,

3, 4 as follows:

618 14 Numerical and Approximation Methods

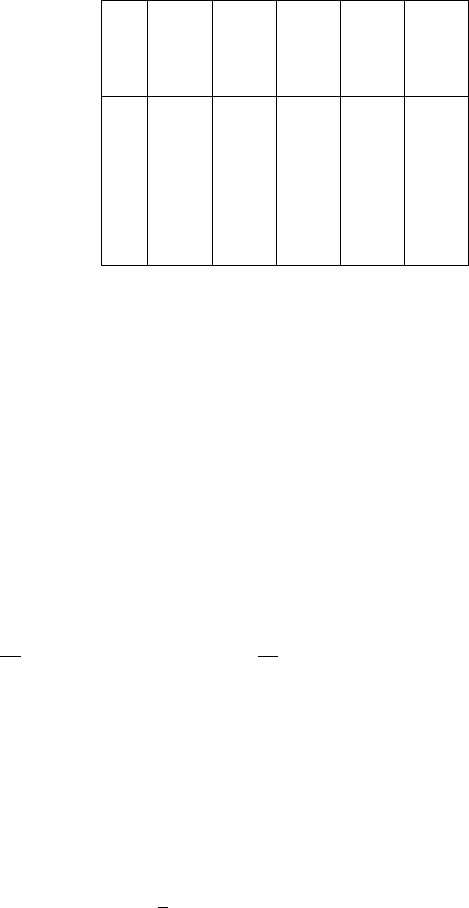
i 0 1 2 3 4

0 1.000 0.000 0.000 0.000 0.000

1 1.000 0.400 0.000 0.000 0.000

2 1.000 0.480 0.160 0.000 0.000

3 1.000 0.560 0.224 0.064 0.000

4 1.000 0.602 0.295 0.103 0.000

As a prototype boundary-value problem, we consider the Dirichlet problem

for the Laplace equation

∇

u ≡ u

+ u

=0, 0 ≤ x ≤ a, 0 ≤ y ≤ b, (14.4.29)

wherethevalueofu (x, y) is prescribed everywhere on the boundary of the

rectangular domain.

The r ectangul ar grid system is the most common and convenient system

for this problem. We choose the vertices of the rectangular domain as the

nodal points and set h = a/m and k = b/n where m and n are positive

integers so that th e domain is divided into mn subrectangles.

The ﬁnite diﬀerence approximation to the Laplace equation (14.4.29) is

i+1,j

− 2u

i,j

+ u

i−1,j

i,j+1

− 2u

i,j

+ u

i,j−1

)=0,(14.4.30)

or,



+ k



i,j

= k

i+1,j

+ u

i−1,j

)+h

i,j+1

+ u

i,j−1

) , (14.4.31)

where 1 ≤ i ≤ m − 1and1≤ j ≤ n − 1.

The prescribed conditions on the boundary of the rectangular domain

determine the values u

0,j

, u

m,j

, u

i,0

,andu

i,n

. For a square grid system

(k = h), equation (14.4.30) becomes

i,j

i+1,j

+ u

i−1,j

+ u

i,j+1

+ u

i,j−1

) . (14.4.32)

This means that the value of u at an interior point is equal to the average

of the value of u at four adjacent points. This is the well known mean value

theorem for harmonic f unction s that satisfy the Laplace equation.

As i and j vary, th e present scheme reduces to a set of (m − 1) (n − 1)

linear non-homogeneous algebraic equations for (m − 1) (n − 1) unknown

values of u at interior grid points. It can be shown the solution of the ﬁnite

14.4 Explicit Finite Diﬀerence Methods 619

diﬀerence equation (14.4.31) converges to the exact solution of the problem

as h, k → 0. The proof of the existence of a solution and its convergence

to the exact solution as h and k tend to zero is essentially based on the

Maximum Modulus Pri nciple. It follows from the ﬁnite diﬀerence equation

(14.4.30) or (14.4.31) that the val ue of |u| at any interior grid point does

not exceed its value at any of the four ad join ing no d al p oints. In other

words, the value of u at P

i,j

cannot exceed its values at the four adjoining

points P

i +

1,j

and P

i,j + 1

. The successive application of this argument at

all interior grid points leads to the conclusion that |u| at the interior grid

points cannot be greater than the maximum value of |u| on the boundary.

This may be recognized as the ﬁnite diﬀerence analogue of the Maximum

Modulus Principle discussed in Section 9.2. Thus, the success of the nu-

merical method is directly associated with the existence of the Maximum

Modulus Principle.

Clearly, the present numerical algorithm deals with a large numb er of

algebraic equations. Even though numerical accuracy can be improved by

making h and k suﬃciently small, there is a major computational diﬃculty

involved in the numerical solution of a large number of equations. It is

possible to handle such a large number of algebraic equations by direct

methods or by iterative methods, but it would be very diﬃcult to obtain

a numerical solution with suﬃcient accuracy. It is therefore necessary to

develop some alternative methods of solution that can be conveniently and

eﬃciently carried out on a computer.

In order to eliminate some of the d rawbacks stated above, one of the nu-

merical schemes, the Liebmann’s iterative method, is useful. In this method

values of u are ﬁrst guessed for all interior grid points in addition to those

given as the boundary points on the edges of the given domain. These values

are denoted by u

(0)

i,j

where the superscript 0 indicates the zeroth iteration.

It is convenient to choose a square grid so that the simpliﬁed ﬁnite diﬀer-

ence equation (14.4.32) can be used. The values of u are calculated for the

next iteration by using (14.4.32) at every interior point based on the values

of u at the present iteration. The sequence of computation starts from the

interior grid point located at the lowest left corner, proceeds upward un-

til reaching the top, and then goes to the bottom of the next vertical line

on the right. This process is repeated until the n ew value of u at the last

interior grid point at the upper right corner has been obtained.

At the starting point, formula (14.4.32) gives

(1)

2,2



(0)

3,2

+ u

(0)

1,2

+ u

(0)

2,3

+ u

(0)

2,1



, (14.4.33)

where u

(0)

1,2

and u

(0)

2,1

are boundary values which remain constant during

the iteration process. They may be replaced, respectively, with u

(1)

1,2

, u

(1)

2,1

(14.4.33). The computation at the next step involves u

(0)

2,2

. Since an improved

value u

(1)

2,2

is available at this time, it will be utilized instead. Hence,

620 14 Numerical and Approximation Methods

(1)

2,3



(0)

3,3

+ u

(1)

1,3

+ u

(0)

2,4

+ u

(1)

2,2



, (14.4.34)

where u

(1)

1,3

is used to replace the constant boundary value u

(0)

1,3

We repeat this argument to obtain a general iteration formul a for com-

putation of u at step (n +1)

(n+1)

i,j



(n)

i+1,j

+ u

(n+1)

i−1,j

+ u

(n)

i,j+1

+ u

(n+1)

i,j−1



. (14.4.35)

This result is valid for any interior p oint, whether it is next to some bound-

ary point or not. If P

i,j

is a true point, the second and fourth terms on the

right side of (14.4.35) represent, respectively, the values of u at the grid

points to the left of and below that point. These values have already been

recomputed according to our scheme, and therefore, carry the superscript

(n + 1). Result (14.4.35) is known as the Liebmann (n +1)thiteration for-

mula. It can be proved that u

(n)

i,j

converges to u

i,j

as n →∞.

Another iteration sch eme similar to (14.4.35) is given by

(n+1)

i,j



(n)

i+1,j

+ u

(n)

i−1,j

+ u

(n)

i,j+1

+ u

(n)

i,j−1



. (14.4.36)

This is called the Richardson iteration formula, and it is also useful. How-

ever, this scheme converges more slowly than that based on (14.4.35).

One of the major diﬃculties of the above methods is the slow rate of con-

vergence. An improved numerical method, the Successive Over-Relaxation

(SOR) scheme gives a faster convergence than the Liebmann or Richardson

method in solving the Laplace (or the Poisson) equation. For a rectangular

domain of square grids, the successive iteration scheme is given by

(n+1)

i,j

= u

(n)

i,j



(n+1)

i−1,j

+ u

(n)

i+1,j

+ u

(n+1)

i,j−1

+ u

(n)

i,j+1

− 4 u

(n)

i,j



, (14.4.37)

where ω is called the acceleration parameter (or relaxation factor)tobe

determined. In general, ω lies in the range 1 ≤ ω<2. The successive

iterations converge fairly rapidly to the desired solution f or 1 ≤ ω<2. The

most rapid rate of convergence i s achieved for the optimum value of ω.

Example 14.4.6. Obtain the standard ﬁve-point formula for the Poisson

equation

+ u

= −f (x, y)inD ⊂ R

with the prescribed value of u (x, y) on the boundary ∂D.

We assume that the domain D is covered by a system of squares with

sides of length h parallel to the x and y axes. Using the central diﬀerence

approximation to the Laplace operator, we obtain

i+1,j

− 2 u

i,j

+ u

i−1,j

i,j+1

− 2 u

i,j

+ u

i,j−1

)=−f

i,j