Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

14.6 Variational Methods and the Euler–Lagrange Equations 631

A self-adjoint operator A on a Hil bert space H is said to be positive if

Au, u≥0 for all u in H, where equality implies that u =0inH. Further,

if there exists a positive constant k such that Au, u ≥k u, u for all u in

H,thenA is called positive deﬁnite in H.

The rest of this section is essentially concerned with linear operators in

a real Hilbert space, which means that the associated scalar ﬁeld involved

is real. Some speciﬁc inner products which will be used in the subsequent

sections include

u, v =



u (x) v (x) dx, u, v =



u (x , y) v (x, y) dx dy,

where D ⊂ R

Example 14.6.4. Determine whether the diﬀerentiable operators (i) A =

d/dx, (ii) A = d

/dx

, and (iii) A = ∇



∂

/∂x





∂

/∂y



are self-

adjoint for functions that are diﬀerentiable in a ≤ x ≤ b or in D ⊂ R

and

vanish on the boundary.

(i) Au, v =







vdx=





−



dx +[u, v]

= u, A

∗

v where A

∗

= −

= A.

Hence, A is not self-adjoint.

(ii) Au, v =







vdx=







−



dx +











dx +



− u









dx = u, Av.

Thus, A is self-adjoi nt.

(iii) Au, v =





∇



vdxdy=



[∇·(∇u) v −∇u ·∇v] dx dy



∂D

(

n ·∇u) vdS−



∇u ·∇vdxdy

= −



(∇u ·∇v) dx dy,

where the divergence theorem is used with the unit outward normal vector

Noting the symmetry of the right hand side in u and v, it follows that

Au, v = Av, u = u, Av.

This means th at the operator A = ∇

is self-adjoint.

632 14 Numerical and Approximation Methods

Example 14.6.5. Use the inn er pro d uct u, v =

***

(u · v) dV and the

operator A = grad to show that A

∗

= −div provided the functions vanish

on the boundary surface ∂D of D.

We use the divergence theorem to obtain

Aφ, v =



(grad φ · v) dV =



[div (φv) − φ div v] dV,



φ (−div v) dV +



∂D

(

n · φv) dS,



φ (−div v) dV = φ, −div v = φ, A

∗

v.

In the theory of calculus of variations it is a common practice to use δu,

u, etc. to denote the ﬁrst and second variations of a function u.Thus,δ

can be regarded as an operator that changes u into δu, u

into δ (u

), and

into δ (u

) with the meaning, δu = εv, δ (u

)=εv

, δ (u

)=εv

where ε is a small arbitrary real parameter. The operators δ, δ

are called

the ﬁrst and second variational operators respectively.

Some simple properties of the operator δ are given by

∂

∂x

(δu)=

∂

∂x

(εv)=ε

∂v

∂x

= δ



∂u

∂x



, (14.6.1)





udx



= ε



vdx=



εvdx =



(δu) dx. (14.6.2)

The variational operator can be interchanged with the diﬀerential and in-

tegral operators, and proves to be very useful in the calculation of the

variation of a functional.

The main task of the calculus of variations is concerned with the problem

of minimizing or maximizing functionals involved in mathematical, physical

and engineering p robl ems. The variational principles have their origins in

the simplest kin d of variational problem, which was ﬁrst considered by Euler

in 1744 and Lagrange in 1760-61.

The classical Euler–Lagrange variational problem is to determine the

extremum value of the functional

I (u)=



F (x, u, u

′

) dx, u

′

, (14.6.3)

with the boundary conditions

u (a)=α and u (b)=β, (14.6.4)

where u b elongs to the class C

([a, b]) of functions which have continuous

derivatives up to second-order in a ≤ x ≤ b,andF has continuous second-

order derivatives with respect to all of its arguments.

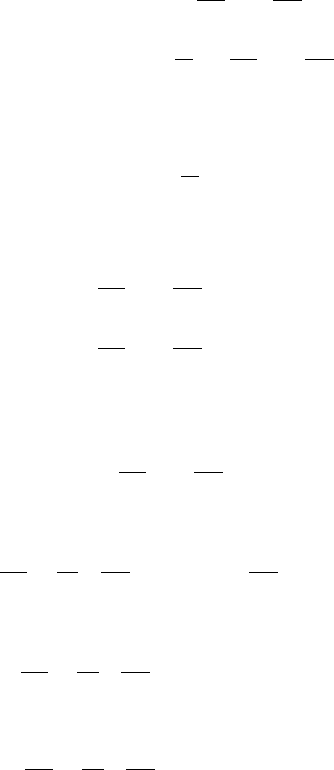
14.6 Variational Methods and the Euler–Lagrange Equations 633

We assume that I (u) has an extremum at some u ∈ C

(2)

([a, b]). Then

we consider the set of all variations u + ǫv for ﬁx ed u where v is an arbi-

trary function belonging to C

([a, b]) such that v (a)=v (b)=0.Wenext

consider the increment of the functional

δI = I (u + εv) − I (u)=



[F (x, u + εv,u

′

+ εv

′

) − F (x, u, u

′

)] dx.

(14.6.5)

From the Taylor series expansion

F (x, u + εv,u

′

+ εv

′

)=F (x, u, u

′

)+ε



∂F

∂u

+ v

′

∂F

∂u

′





∂F

∂u

+ v

′

∂F

∂u

′



+ ··· ,

it follows from (14.6.5) that

I (u + εv)=I (u)+εδI +

I + ··· , (14.6.6)

where the ﬁrst and second variations of I are given by

δI =





∂F

∂u

+ v

′

∂F

∂u

′



dx, (14.6.7)

I =





∂F

∂u

+ v

′

∂F

∂u

′



dx. (14.6.8)

The necessary condition for the functional I (u) to have an extremum (that

is, I (u) is stationary at u) is that th e ﬁrst variation becomes zero at u so

0=δI =





∂F

∂u

+ v

′

∂F

∂u

′



dx (14.6.9)

which is, by partial integration of the second integral,





∂F

∂u

−



∂F

∂u

′



vdx+



∂F

∂u

′



Because v (a)=v (b) = 0, this means that





∂F

∂u

−



∂F

∂u

′



vdx=0. (14.6.10)

Since v is arbitrary in a ≤ x ≤ b, it follows from (14.6.10) that

∂F

∂u

−



∂F

∂u

′



=0. (14.6.11)

This is the famous Euler–Lagrange equation. We therefore can state:

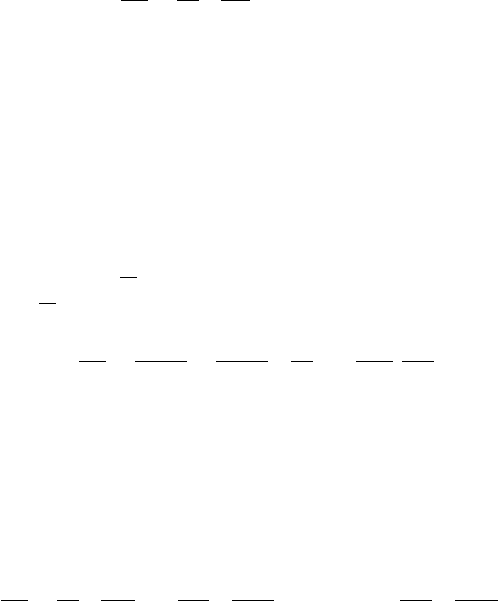
634 14 Numerical and Approximation Methods

Theorem 14.6.1. A necessary condition for the functional I (u) to be sta-

tionary at u is that u is a solution of the Euler–Lagrange equation

∂F

∂u

−



∂F

∂u

′



=0,a≤ x ≤ b (14.6.12)

with

u (a)=α, u (b)=β. (14.6.13)

This is called the Euler–Lagrange variational principle.

Note that, in general, equation (14.6.12) is a nonlinear second-order

ordinary diﬀerential equations, and, although such an equation is very dif-

ﬁcult to solve, still it seems to be more accessible analytically than the

functional (14.6.3) from which it is derived.

The derivative

in (14.6.12) can be computed by recalling u = u (x)

and u

′

, and equation (14.6.12) becomes

∂F

∂u

−

∂

∂x∂u

′

−

∂

∂u∂u

′





−

∂

∂u

′2

∂x

=0.

It is left to the reader to verify that the functional with one independent

variable and nth-order derivatives in the for m

I (u)=



F (x, u, u

,...,u

,...,) dx

admits the Euler–Lagrange equation

∂F

∂u

−



∂F

∂u





∂F

∂u



− ...(−1)



∂

∂u



=0.

After we have determined the f unction u which makes I (u) stationary,

the question of the nature of the extremu m arises, that is, its minimum,

maximum, or saddle point properties. To answer this question, we look at

the second variation deﬁned in (14.6.8). If terms of O





can be neglected

in (14.6.6), or if they vanish for the case of quadratic F, it follows from

(14.6.6) that a necessary condition for the functional I (u)tohaveamini-

mum I (u) ≥ I (u

)atu = u

is that δ

I ≥ 0, for I (u) to have a maximum

I (u) ≤ I (u

)atu = u

is that δ

I ≤ 0atu = u

respectively for all

admissible values of v. These results enable us to determine the upper or

lower bounds for the stationary value I (u

) of the functional.

Example 14.6.6. Find out the shortest distance between given points A and

B in the (x, y)-plane.

Suppose APB is any curve in the plane through A and B,ands =

arcAP . The problem is to determine the curve for which the functional

14.6 Variational Methods and the Euler–Lagrange Equations 635

I (y)=



ds, (14.6.14)

is a minimum.

Since ds/dx =



1+y

′2



, functional (14.6.14) becomes

I (y)=





1+y

′2



dx. (14.6.15)

In this case, F =



1+y

′2



which depends on y

′

only, so ∂F/∂y =0.

Hence, the Euler–Lagrange equation (14.6.12) becomes



∂F

∂y

′



=0.

This gives the diﬀerential equation

′′

=0. (14.6.16)

This means that the curvature for all points on the curve AB is zero. Hence,

the path AB is a straight line. It follows from the integration of (14.6.16)

that y = mx + c is a two-parameter family of straight lines.

Example 14.6.7. (Fermat principle in optics). In an optically homogeneous

isotro-pic medium, light travels from one point A to another point B along

thepathforwhichthetraveltimeisminimum.

The velocity of light v is the same at all points of the medium; hence, the

minimum time is equivalent to the minimum path length. For simplicity,

consider a path joining the two points A and B in the (x, y)-plane. The

time to travel an elementary arc length ds is ds/v. Thus, the variational

problem is to ﬁnd the path for which





1+y

′2





F (y, y

′

) dx (14.6.17)

is a minimum, where y

′

= dy/dx,andv = v (y).

When F is a function of y and y

′

, the Euler–Lagrange equation (14.6.12)

becomes

(F − y

′

)=0. (14.6.18)

This follows from the result

(F − y

′

F (y, y

′

) − y

′′

′

− y

′

)

= y

′

+ y

′′

− y

′′

− y

′

)

= y

′



−

′

)



=0, by (14.6.12) .

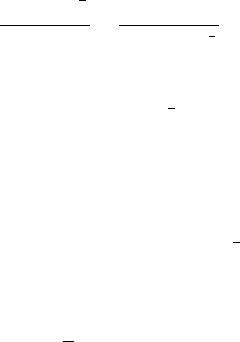
636 14 Numerical and Approximation Methods

Hence,

F − y

′

= constant, (14.6.19)



1+y

′2



−

′2

v (1 + y

′2

)

= constant,

−1



1+y

′2



−

= constant. (14.6.20)

In order to give a simple physical interpretation, we rewrite (14.6.20) in

terms of th e angle φ made by the tangent to the minimum path with the

vertical y-axis so that

sin φ =



1+y

′2



−

Hence,

sin φ = constant = K (14.6.21)

for all points on the minimum curve. For a ray of light, (1/v)mustbe

directly proportional to the refractive index n of the medium through which

light is travelling. Equation (14.6.21) is called the Snell law of refraction of

light. Often this law is stated as

n sin φ = constant. (14.6.22)

(A) Hamilton Pr inciple

The diﬀerence between the kinetic energy T and the potential energy V

of a dynamical system is denoted by L = T − V . The quantity L is called

the Lagrangian of the system. The Hamilton principle states that the ﬁrst

variation of the time integral of L is zero, that is,



Ldt= δ



(T − V ) dt =0. (14.6.23)

This result is supposed to be valid for all dynamical systems whether they

are conservative or nonconservative.

For a conservative system the force ﬁ eld F = −∇V and T + V = C,

where C is a constant, and so (14.6.23) gives the principle of least action

δA =0,A=



Ldt, (14.6.24)

where A is called the action integral or simply the action of the system.

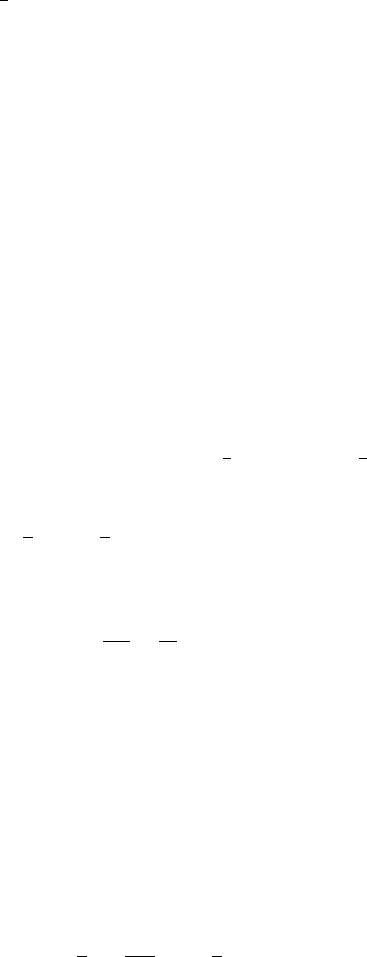
14.6 Variational Methods and the Euler–Lagrange Equations 637

Example 14.6.8. Derive the Newton second law of motion from the Hamil-

ton principle.

Consider a particle of mass m at the position r =(x, y, z)whichis

moving under the action of a ﬁeld of force F. The kinetic energy of the

particle is T =

, and the variation of work done is δW = F · δr and

δV = −δW. Thus, th e Hamilton principle for the system is

0=δ



(T − V ) dt =



(δT −δV ) dt =



r · δ

r + F · δr) dt.

Integrating this result by parts and noting that δr vanishes at t = t

and t = t

, we obtain



r − F) · δr dt =0.

This is true for every virtual displacement δr, and hence, the integrand

must vanish, that is,

r = F. (14.6.25)

This is the celebrated Newton second law of motion.

Example 14.6.9. Derive the equation for a simple harmonic oscillator in a

non-resisting medium from the Hamilton principle.

For a simple harmonic oscillator, T =

m ˙x

and V =

mω

. Accord-

ing to the Hamilton principle





m ˙x

−

mω



dt = δ



F (x, ˙x) dt =0.

This leads to the Euler–Lagrange equation

∂F

∂x

−

(m ˙x)=0,

¨x + ω

x =0. (14.6.26)

This is the equation for the simple harmonic oscillator.

Example 14.6.10. A straight uniform elastic beam of length l, line density ρ,

cross-sectional moment of inertia I, and modulus of elasticity E is ﬁxed at

each end. The beam performs small transverse oscillations in the horizontal

(x, y)-plane. Derive the equation of motion of the beam.

The potential energy of the elastic beam is

V =



dx =



EIy

′′2

dx,

638 14 Numerical and Approximation Methods

where the bending moment M is proportional to the curvature so that

M = EI

′′

(1 + y

′2

)

∼ EI y

′′

for small y

′

The variational principle gives



(T − V ) dt = δ



F (y

′′

, ˙y) dt =0,

where

F (y

′′

, ˙y)=





ρ ˙y

− EI y

′′2



dx.

This principle leads to the Euler–Lagrange equation

−





ρ¨y + EIy

(iv)



dx =0,

ρ¨y + EIy

(iv)

=0. (14.6.27)

This represents the partial diﬀerential equation of the transverse vibration

of the beam.

(B) The Generalized Coordinates, Lagrange Equation, and

Hamilton Equation

The Euler–Lagrange analysis of a dynamical system can be extended to

more complex cases where the conﬁguration of the system is described by

generalized coordinates q

, q

, ..., q

. Without loss of generality, we consider

a system of three variables where the familiar Cartesian coordinates x, y,

z can be expressed in terms of the generalized coordinates q

, q

x = x (q

) ,y= y (q

) ,z= z (q

) . (14.6.28)

For example, if (q

) represents the cylindrical polar coordinates

(r, θ, z), the above result becomes

x = r cos θ, y = r sin θ, z = z.

Since the coordinates are functions of time t, we obtain the following

result by diﬀerentiation

˙x =

∂x

∂q

˙q

∂x

∂q

˙q

∂x

∂q

˙q

(14.6.29)

14.6 Variational Methods and the Euler–Lagrange Equations 639

with similar expressions for ˙y and ˙z.

If these results are substituted into T =



˙x

+˙y

+˙z



and V =

V (x, y, z), then both T and V can be written in terms of the generalized

coordinates q

and the generalized velocities ˙q

,as

T = T (q

;˙q

, ˙q

) ,V= V (q

) , (14.6.30)

so that the Lagrangian has the form

L = T − V = L (q

, ˙q

) . (14.6.31)

The Hamilton principle gives



L (q

, ˙q

) dt =0. (14.6.32)

The simple variation of this integral with ﬁxed end points, the inter-

change of the variation operations and time derivatives f or the variation of

the generalized velocities, and then integration by parts yield







i=1



∂L

∂q

−



∂L

∂ ˙q



δq



dt =0, (14.6.33)

where the integrated components vanish because of the conditions δq

(i =1, 2, 3) at t = t

and t = t

When the generalized coordinates are independent and the variations

δq

are independent for all t in (t

), the coeﬃcients of the variations δq

vanish independently for arbitrary values of t

and t

. This means that the

integrand in (14.6.33) vanishes, that is,



∂L

∂ ˙q



−

∂L

∂q

=0,i=1, 2, 3. (14.6.34)

These are called the Lagrange equations of motion.

If a particle of mass m at position r =(x

) moves under the

action of a conservative force ﬁeld F

= −∂V/∂x

, the Lagrangian function

L = T − V =



˙x

+˙x



− V (x

) . (14.6.35)

Consequently,

∂L

∂ ˙x

= m ˙x

∂L

∂x

= −

∂V

∂x

= F

. (14.6.36)

The former represents the momentum of the particle and the latter is the

force acting on the particle. In view of (14.6.36), the Lagrange equation

(14.6.34) gives the Newton second law of motion in the form

(m ˙x

)=F

. (14.6.37)

640 14 Numerical and Approximation Methods

Example 14.6.11. Apply the Lagrange equations of motion to derive the

equations of motion of a particle under the action of a central force,

−mF (r)wherer is the distance of the particle of mass m from the center

of force.

It is convenient to use the polar coordinates r and θ. In terms of the

generalized coordinates q

= r and q

= θ,wewrite

x = r cos θ = q

cos q

,y= r sin θ = q

sin q

The kinetic energy T is

T =



˙x

+˙y





˙r

+ r





˙q

+ q

˙q



. (14.6.38)

Since F = ∇V ,thepotentialis

V (r)=



F (r) dr =



F (q

) dq

. (14.6.39)

Then, the Lagrangian L is

L = T − V =





˙q

+ q

˙q



− 2



F (q

) dq



. (14.6.40)

Thus, the Lagrange equations (14.6.34) wit h i = 1, 2, 3 give the equations

of motion

¨q

− q

˙q

+ F (q

)=0,



˙q



=0. (14.6.41)

In term of the polar coordinates, these equations become

¨r − r

= −F (r) ,





=0. (14.6.42ab)

Equation (14.6.42b) gives immediately

θ = h, (14.6.43)

where h is a constant. In this case, r

θ represents the transverse velocity

component, and mr

θ = mh is the constant angular momentum of the

particle about the center of force.

Introducing r =1/u, we obtain

˙r =

= −

dθ

= −h

dθ

¨r =

= −h



dθ



= −h

dθ

= −h

dθ

Substituting these into (14.6.42a) gives