Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


14.9 The Kantorovich Method 661
∂F
∂a
k
−
d
dx
∂F
∂a
′
k
=0,k=1, 2, 3,...,n. (14.9.9)
This system of ordinary differential equations for the functions a
k
is to be
solved with the boundary conditions a
k
(a)=a
k
(b)=0,k =1,2,..., n.
Consequently, the requi red solution u
n
(x, y) is determined.
Example 14.9.1. Find a solution of the torsion problem governed by the
Poisson equation ∇
2
u = −2 in the rectangle D = {(x, y):−a<x<a,
−b<y<b} with the boundary condition u =0on∂D = {x =+
a, y =+b}.
In the first approximation, we seek a solution in the form
u
1
(x, y)=
y
2
− b
2
a
1
(x)
which satisfies the boundary condition on y =+
b. We next determine
a
1
(x)sothata
1
(x)=a
1
(−a)=0.
The functional associated with the p roblem is
I (u)=
D
u
2
x
+ u
2
y
− 4u
dx dy.
Substituting u
1
into this functional yields
I (u
1
)=
a
−a
dx
b
−b
"
y
2
− a
2
2
a
′
2
1
+4y
2
a
2
1
− 4
y
2
− b
2
a
1
#
dy
=
a
−a
16
15
b
5
a
′
2
1
+
8
3
b
3
a
2
1
+
16
3
b
3
a
1
dx.
The Euler equation for the functional is
a
′′
1
−
5
2b
2
a
1
−
5
2b
2
=0.
This is a linear ordinary differential equation for a
1
with constant coeffi-
cients, and has the general solution
a
1
(x)=A cosh kx + B sinh kx − 1,k=
1
b
5
2
,
where the constants A and B are determined by the boundary conditions
a
1
(a)=a
1
(−a)=0sothatB = 0 and
A =
1
cosh ka
.
Thus, an approximate solution is
u
1
(x, y)=
y
2
− b
2
cosh kx
cosh ka
− 1
.
662 14 Numerical and Approximation Methods
Finally, the torsional moment is given by
M =2µα
D
udxdy∼ 2µα
D
u
1
dx dy
=2µα
a
−a
cosh kx
cosh ka
− 1
dx
b
−b
y
2
− b
2
dy
=
16
3
µαb
3
a
1 −
1
ka
tanh (ak)
.
Example 14.9.2. Solve the Poisson equation ∇
2
u = −1 in a triangular do-
main D bounded by x = a and y =+
x/
√
3
with u =0on∂D.
The associated functional for the Poisson equation is
I (u)=
D
u
2
x
+ u
2
y
− 2u
dx dy.
We seek the Kantorovich solution in the first approximation
u (x , y) ∼
y
2
−
x
2
3
u
1
(x)
so that u
1
(a)=0.
Substituting the solution into I (u)gives
I (u
1
)=
a
0
dx
x/
√
3
−x/
√
3
y
2
−
x
2
3
u
′
1
−
2xu
1
3
2
+
+4y
2
u
2
1
(x) − 2
y
2
−
x
2
3
u
1
dy
=
8
135
√
3
a
0
2x
5
u
′
2
1
+10x
4
u
1
u
′
1
+30x
3
u
2
1
+15x
3
u
1
dx.
The Euler equation for this functional is
4
x
2
u
′′
1
+5xu
′
1
− 5u
1
=15.
This is a nonhomogeneous ordinary differential equation of order two. We
seek a solution of the corresponding homogeneous equation in the form x
r
where r is determined by the equation (r − 1) (r + 5) = 0. The p articular
integral of the equation is u
1
= −
3
4
. Hence, the general solution is
u
1
(x)=Ax + Bx
−5
−
3
4
,
where the constants A and B are to be determined by the boundary con-
ditions. For the bounded solution, B ≡ 0. The condition u
1
(a) = 0 implies
A =(3/4a). Therefore, the final solution is
u (x , y)=
3
4
x
a
− 1
y
2
−
x
2
3
.
14.10 The Finite Element Method 663
14.10 The Finite Element Method
Many problems in mathematics, science and engineering are not simple
and cannot be solved by exact closed-form analytical formulas. It is often
necessary to obtain approximate numerical or asymptotic solutions rath er
than exact solutions. Many numerical methods that have evolved over the
years reduce algebraic or differential equations to discrete form which can
be solved easily by computer. However, if the numerical method is not care-
fully chosen, the numerically computed solution may not be anywhere close
to the true solution. Another problem is that the computation for a difficult
problem may take so long that it is impractical for a computer to carry out.
The most commonly used numerical methods are finite differences that give
pointwise approximations of the governing equations. These methods can
be used successfully to solve many fairly difficult problems, but their major
weakness is that they are not suitable f or problems with irregular geome-
tries, curved boundaries or unusual boundary condition s. For example, the
finite difference methods are not particularly effective for a circular d omain
because a circle cannot be accurately partitioned into rectangles. However,
there are other numerical methods including the finite element method and
the boundary element method.
Unlike fin ite difference methods, the finite element method can be used
effectively to determine fairly accurate approximate solutions to a wide
variety of governing equations defined over irregular r egions. The entire so-
lution domain can be modeled analytically or approximated by replacing it
with small, interconnected discrete finite elements (hence the name finite
element). The solution is then approximated by extremely simple functions
(linear fu nction s) on these small elements such as triangles. These small ele-
ments are collected together and requirements of continuity and equilibrium
are satisfied between neighboring elements.
In a nutshell, the basic idea of the finite element method (FEM) con-
sists of decomposing a given domain into a set of finite elements of arbitrary
shape and size. This decomposition is usually called a mesh or a grid with
the restriction that elements cannot overlap nor leave any part of the do-
main uncovered. For each element, a certain number of points is introduced
that can be located on the edges of the elements or inside. These points are
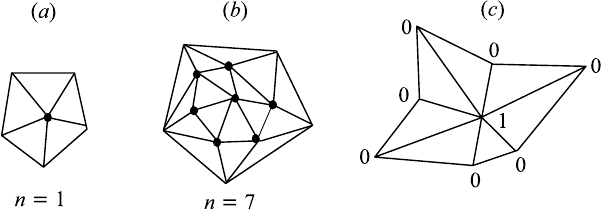
called nodes that are usually vertices of triangles as shown in Figure 14.10.1.
Finally, these nodes are used to approximate a function under consideration
over the whole domain by interpolation in the finite elements.
Historically, the finite element method was developed originally to study
stress fields in complicated aircraft structures in the early 1960s. Subse-
quently, it has been extended and widely applied to find approximate solu-
tions to a wide variety of problems in mathematics, science, and engineering.
It was Richard Courant (1888–1972) who first introduced piecewise contin-
uous functions defined over triangular domains in 1943; he then used these
triangular elements combined with the principle of minimum potential en-
664 14 Numerical and Approximation Methods
ergy to study the St. Venant torsion problem in continuum mechanics. He
also d escribed element properties and finite element equations based on a
variational principle. In 1965, the finite element method received an even
broader interpretation when Zienkiewicz and Cheung (1965) suggested that
it is applicable to all field problems that can be cast in variational form.
During the late 1960s and early 1970s, considerable attention has been given
to errors, bounds and convergence criteria for finite element approximations
to solutions of various problems in continuum mechanics.
In order to develop the finite element method, we recall the celebrated
Euler–Lagrange equation (14.6.12) with u (a)=α and u (b)=β. We divide
the interval a ≤ x ≤ b into n parts by the R
n+1
set: a = x
0
<x
1
<x
2
<
...<x
n
= b.Eachsuchsubintervaliscalledanelement. In general, the
length of the elements need not be equal, though for simplicity, we assume
that they are equal in length so that h =
1
n
(b − a). We set u
k
= u (x
k
),
k =0, 1, 2,...,n so that u
0
(x
0
)=α and u
n
(x
n
)=β, while u
1
, u
2
, ...,
u
n−1
are unknown quantities. We next rewrite the fu nctional (14.6.3) as
I (u)=
x
1
x
0
F (x, u, u
′
) dx +
x
2
x
1
F (x, u, u
′
) dx + ...+
x
n
x
n−1
F (x, u, u
′
) dx.
(14.10.1)
We define a p iecewise linear interpolating function L (x)ofu
i
as the
function which i s continuous on [a, b] and whose graph consists of straight
line segments joining the consecutive pairs of points (x
k
,u
k
), (x
k+1
,u
k+1
)
for k =0,1,2,...,(n − 1), that is,
L (x)=u
k
+
1
h
(u
k+1
− u
k
)(x − x
k
) ,x
k
≤ x ≤ x
k+1
, (14.10.2)
where k =0,1,2,...,(n − 1).
Substituting L for u and L
′
for u
′
in (14.10.1) and assuming that the
integrals can be computed exactly yields
I
n−1
= I
n−1
(u
1
,u
2
,...,u
n−1
) . (14.10.3)
We next find the minimum of I
n−1
by solving the system of equations
∂I
n−1
∂u
k
=0,k=1, 2,...,(n − 1) . (14.10.4)
The solution of this system (14.10.4) is then substituted into (14.10.2) to
obtain a continuous, piecewise linear approximation for the exact solution
u (x).
Example 14.10.1. (The Dirichlet problem for the Poisson equation in a
plane).
We consider the problem
14.10 The Finite Element Method 665
−△u = f (x, y)inD , (14.10.5)
u = 0 on the boundary ∂D. (14.10.6)
The region D is first triangulated so that it is approximated by a region
D
n
which is the union of a finite number of triangles as shown in Figures
14.10.1 (a) and 14.10.1 (b). We denote the interior vertices by V
1
, V
2
, ...,
V
n
.
We next choose n trial functions v
1
(x, y), v
2
(x, y), ..., v
n
(x, y), one for
each interior vertex. Each trial function v
m
(x, y)isassumedtobeequalto
1 at its vertices V
m
and equal to zero at all other vertices as in shown in
Figure 14.10.1 (c).
Each linear trial function v
m
(x, y)=ax + by + c,wherea, b,andc
are different for each trial function and for each triangle. This requir ement
determines v
m
(x, y) uniquely. Indeed, its graph is simply a pyramid of unit
height with its peak at V
m
and it is zero on all the triangles which do not
touch V
m
.
We next approximate the solution u (x, y) by a linear combination of
the v
m
(x, y)sothat
u
n
(x, y)=a
1
v
1
(x, y)+a
2
v
2
(x, y)+...+ a
n
v
n
(x, y)=
n
m=1
a
m
v
m
(x, y) ,
(14.10.7)
where the coefficients a
1
, a
2
, ..., a
n
aretobedetermined.
We multiply the Poisson equation (14.10.5) by any function v (x, y)
which is zero on ∂D an d next use Green’s first identity to obtain
D
∇u ·∇vdxdy=
D
f v dx dy. (14.10.8)
We assume that (14.10.8) is valid only for the first n trial functions so
that v = v
k
for k =1,2,..., n. With u (x, y)=u
n
(x, y)andv (x, y)=
v
k
(x, y), result (14.10.8) becomes
Figure 14.10.1 (a), (b), and (c). Triangular elements.
666 14 Numerical and Approximation Methods
n
m=1
a
m
D
(∇u
m
·∇v
k
) dx dy
=
D
fv
k
dx dy. (14.10.9)
This is a system of n linear equations, where m =1,2,..., n in the n
unknown coefficients a
m
,andcanberewrittenintheform
n
m=1
α
mk
a
m
= f
k
,k=1, 2,...,n, (14.10.10)
where
α
mk
=
D
(∇u
m
·∇v
k
) dx dy, f
k
=
D
fv
k
dx dy. (14.10.11)
Consequently, the finite element method leads to finding α
mk
and f
k
from
(14.10.11) and then solving (14.10.10). Finall y, the approximate value of
the solution u (x, y) is then given by (14.10.7).
Several comments are in order. First, the trial functions v
m
(x, y) depend
on the geometry of the problem and are completely known. Second, the
approximate solution u
n
(x, y) vanishes on the boundary ∂D
n
.Third,ata
vertex V
i
=(x
i
,y
i
),
u
n
(x
i
,y
i
)=a
i
v
i
(x
i
,y
i
)+...+ a
n
v
n
(x
i
,y
i
)=
n
r=1
a
r
v
r
(x
i
,y
i
)=a
i
where
v
r
(x
k
,y
k
)=
⎧
⎨
⎩
0,r= k
1,r= k.
Fourth, the coefficients a
i
are exactly the values of the approximate solution
at the vertices V
i
=(x
i
,y
i
).
Example 14.10.2. We consider the variational problem of finding the ex-
tremes of the functional
I (u)=
6
0
u
′2
+ u
2
− 2u − 2xu
dx (14.10.12)
with the boundary conditions u (0) = 1 and u (6) = 7.
We divide 0 ≤ x ≤ 6 into three equal parts of length h =2byx
0
=0,
x
1
=2,x
2
= 4 and x
3
= 6. We set u
k
= u (x
k
)sothatu
0
= u (0) = 1 and
u
3
= u (6) = 7, while u
1
and u
2
are unknown quantities. We have
F (x, u, u
′
)=u
′2
+ u
2
− 2u − 2xu (14.10.13)
so that
14.10 The Finite Element Method 667
I =
2
0
F (x, u, u
′
) dx +
4
2
F (x, u, u
′
) dx +
6
4
F (x, u, u
′
) dx. (14.10.14)
We take
L (x)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
u
0
+
1
2
(u
1
− u
0
) x, 0 ≤ x ≤ 2
u
1
+
1
2
(u
2
− u
1
)(x − 2) , 2 ≤ x ≤ 4
u
2
+
1
2
(u
3
− u
1
)(x − 4) , 4 ≤ x ≤ 6,
, (14.10.15)
so that its derivative is
L
′
(x)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
1
2
(u
1
− u
0
) , 0 ≤ x ≤ 2
1
2
(u
2
− u
1
) , 2 <x≤ 4
1
2
(u
3
− u
1
) , 4 <x≤ 6.
(14.10.16)
Substituting (14.10.15)–(14.10.16) into (14.10.14) and using (14.10.13) we
get
I =
2
0
u
1
− u
0
2
2
+
u
0
+
1
2
(u
1
− u
0
) x
2
− 2
u
0
+
1
2
(u
1
− u
0
) x
−2x
u
0
+
1
2
(u
1
− u
0
) x
dx
+
4
2
u
2
− u
1
2
2
+
u
1
+
1
2
(u
2
− u
1
)(x − 2)
2
−2
u
1
+
1
2
(u
2
− u
1
)(x − 2)
− 2x
u
1
+
1
2
(u
2
− u
1
)(x − 2)
dx
+
6
4
u
3
− u
1
2
2
+
u
2
+
1
2
(u
3
− u
1
)(x − 4)
2
−2
u
2
+
1
2
(u
3
− u
1
)(x − 4)
−2x
u
2
+
1
2
(u
3
− u
1
)(x − 4)
dx.
Using the known values of u
0
and u
3
and integrating we obtain (n =3)
I
2
=
7
3
u
2
1
+ u
2
2
−
1
3
u
1
u
2
−
37
3
u
1
−
67
3
u
2
−
101
3
.
Consequently, equation (14.10.4) gives two equations
∂I
2
∂u
1
=
14
3
u
1
−
1
3
u
2
−
37
3
=0,
∂I
2
∂u
2
= −
1
3
u
1
+
14
3
u
2
−
67
3
=0.
668 14 Numerical and Approximation Methods
Thus, the solutions f or u
1
and u
2
are u
1
= 3 and u
2
=5.
Putting these values into (14.10.15) leads to the approximate solution
L (x)=1+x, 0 ≤ x ≤ 6. (14.10.17)
In this problem, the Euler–Lagrange equation for (14.10.12) is given by
u
′′
− u = −(1 + x) . (14.10.18)
Solving this equation with u (0) = 1 and u (6) = 7 yields the exact solution
u (x)=1+x.
In this example, the exact and approximate solutions are identical due
to the simplicity of the problem. In general, these solutions will be different.
We close this section by adding some comments on another numerical
technique known as the boundary element method (boundary integral equa-
tion method). This method was widely used in early research in solid me-
chanics, fluid mechanics, potential theory and electromagnetic theory. How-
ever, the major breakthrou gh in the boundary integral equation method
came in 1963 when two classic papers were published by Jaswon (1963) and
Symm (1963). The boundary element method is based on the mathemati-
cal aspect of finding the Green’s function solution of differential equations
with prescribed boundary conditions. It also uses Green’s theorem to re-
duce a volume problem to a surface problem, and a surface problem to a
line problem. This technique is not only very useful but also very accurate
for linear problems, especially for three dimensional problems with rapidly
changing variables in fracture and contact problems in solid mechanics.
However, this method is computationally less efficient than the finite ele-
ment method, and is not widely used in industry. It is fairly popular for
finding numerical solutions of acoustic problems. Since the early 1970s the
boundary element method has continu ed to develop at a fast pace and has
been extended to include a wide variety of linear and nonlinear problems
in continuum mechanics.
14.11 Exercises
1. Obtain the explicit finite difference solution of the problem
u
tt
− 4u
xx
=0, 0 <x<1,t>0,
u (0,t)=u (1,t)=0,t≥ 0,
u (x , 0) = sin 2πx, u
t
(x, 0) = 0, 0 ≤ x ≤ 1.
Compare the numerical solution with the analytical solution
u (x , t)=cos4πt sin 2πx
at several points.

14.11 Exercises 669
2. (a) Calculate an explicit finite difference solution of the wave equation
u
xx
− u
tt
=0, 0 <x<1,t>0,
satisfying the boundary conditions
u (0,t)=u (1,t)=0,t≥ 0,
and the initial conditions
u (x , 0) =
1
8
sin πx, u
t
(x, 0) = 0, 0 ≤ x ≤ 1.
Show that the exact solution of the problem is
u (x , t)=
1
8
cos πt sin πx.
Compare the two solutions at several points.
(b) Solve the wave equation in (a) with the same boundary data and
the initial data
u (x , 0) = sin πx, u
t
(x, 0) = 0, 0 ≤ x ≤ 1.
3. Use the Lax–Wendroff method to find a numerical solution of the prob-
lem
u
x
+ u
t
=0,x>0,t>0,
u (x , 0) = 2 + x, x > 0,
u (0,t)=2− t, t > 0.
Show that the exact solution of the problem is
u (x , t)=2+(x − t) .
Compare the two solutions at various points.
4. Show that the finite difference approximation to the equation
au
t
+ bu
x
= f (x, t)
is
u
i,j+1
−
1
2
(u
i+1,j
+ u
i−1,j
)+
εb
2a
(u
i+1,j
− u
i−1,j
) − f
i,j
=0,
where a, b are constants and ε = k/h.

670 14 Numerical and Approximation Methods
5. Obtain a finite difference solution of the heat conduction problem
u
t
= κu
xx
, 0 <x<l, t>0,
with the boundary conditions
u (0,t)=u (l, t)=0,t>0,
and the initial condition
u (x , 0) =
4x
l
(l − x) , 0 ≤ x ≤ l.
6. (a) Find an explicit finite difference solution of the parabolic system
u
t
= u
xx
, 0 <x<1,t>0,
u (0,t)=u (1,t)=0,t>0,
u (0,t)=sinxπ on 0 ≤ x ≤ 1.
Compare the numerical results with the analytical solution
u (x , t)=e
−π
2
t
sin πx,
at t =0.5andt =0.05.
(b) Prove that the Richardson finite difference scheme for problem 6(a)
is
u
i,j+1
= u
i,j−1
+2εδ
2
x
u
i,j
.
Hence, show that the exact solution of this equation is
u
i,j
=
A
1
α
j
1
+ A
2
α
j
2
sin πhi,
where α
1
and α
2
are the roots of the quadratic equation
x
2
+8εx sin
2
(πh/2) − 1=0.
7. Using four internal grid p oints, find the explicit finite difference solution
of the Dirichlet problem
∇
2
u ≡ u
xx
+ u
yy
=0, 0 <x<1, 0 <y<1,
u (x , 0) = x (1 − x) ,u(x, 1) = 0 on 0 ≤ x ≤ 1,
u (0,y)=u (1,y)=0, on 0 ≤ y ≤ 1.
Compare the numerical solution with the exact analytical solution
u (x , y)=
4
π
3
∞
n=0
2
(2n +1)
3
sin nπx sinh nπ (1 − y)
sinh nπ
at the point (x, y)=
1
3
,
1
3
.
