Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


15.5 Hankel Transforms 691
15.5 Hankel Transforms
f (r) order
n
˜
f
n
(k)=
∞
0
rJ
n
(kr) f (r) dr
1 H (a − r) 0
a
k
J
1
(ak)
2 exp (−ar) 0 a
a
2
+ k
2
−
3
2
3
1
r
exp (−ar)
0
a
2
+ k
2
−
1
2
4
a
2
− r
2
H (a − r)
0
4a
k
3
J
1
(ak) −
2a
2
k
2
J
0
(ak)
5 a
a
2
+ r
2
−
3
2
0 exp (−ak)
6
1
r
cos (ar)
0
k
2
− a
2
−
1
2
H (k − a)
7
1
r
sin (ar)
0
a
2
− k
2
−
1
2
H (a − k)
8
1
r
2
(1 − cos ar)
0 cosh
−1
a
k
H (a − k)
9
1
r
J
1
(ar)
0
1
a
H (a − k) ,a>0
10 Y
0
(ar) 0
2
π
a
2
− k
2
−1
11 K
0
(ar) 0
a
2
+ k
2
−1
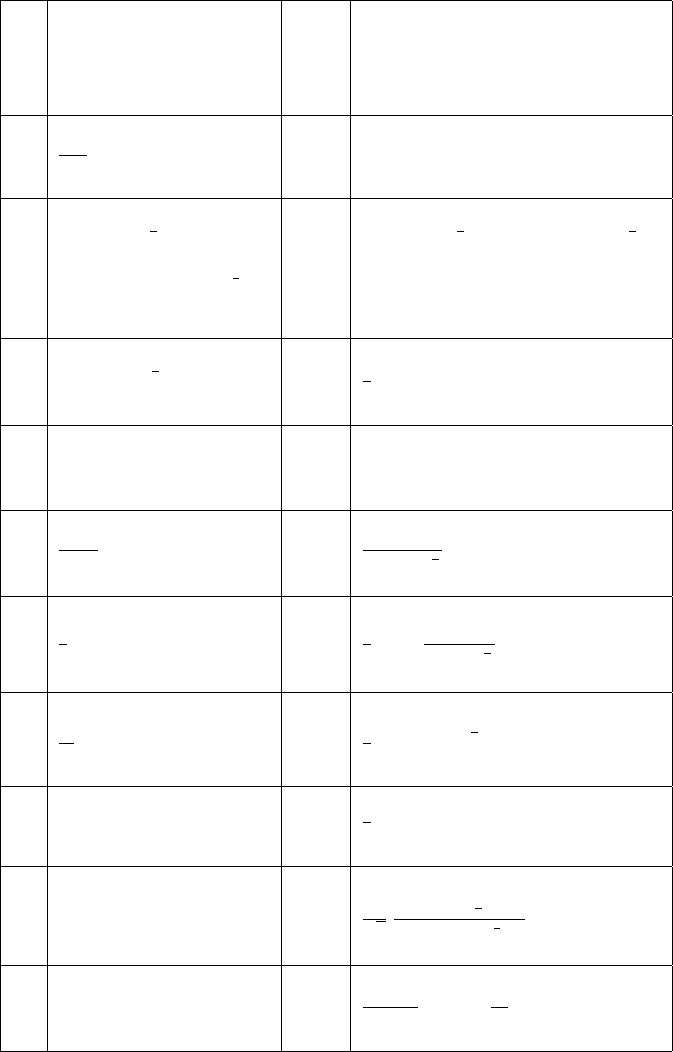
692 15 Tables of Integral Transforms
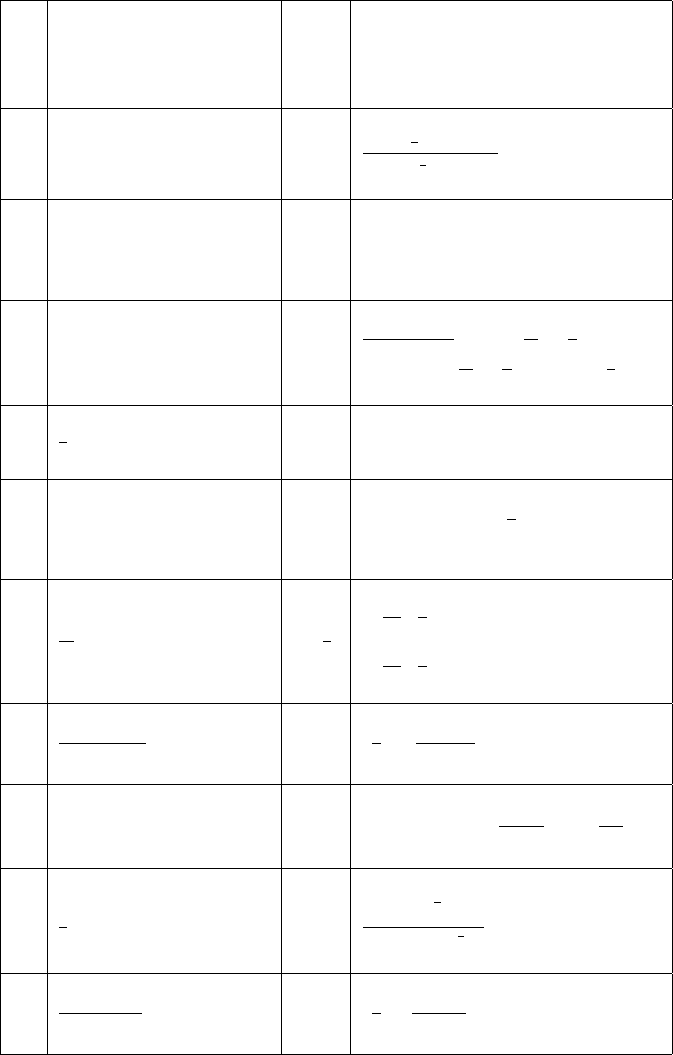
f (r) order
n
˜
f
n
(k)=
∞
0
rJ
n
(kr) f (r) dr
12
δ ( r)
r
0 1
13
r
2
+ b
2
−
1
2
×exp
(
−a
r
2
+ b
2
1
2
)
0
k
2
+ a
2
−
1
2
exp
(
−b
k
2
+ a
2
1
2
)
14
r
2
+ a
2
−
1
2
0
1
k
exp (−ak )
15 exp (−ar) 1 k
a
2
+ k
2
−3/2
16
sin ar
r
1
aH(k−a)
k(k
2
−a
2
)
1
2
17
1
r
exp (−ar)
1
1
k
1 −
a
(k
2
+a
2
)
1
2
18
1
r
2
exp (−ar)
1
1
k
"
k
2
+ a
2
1
2
− a
#
19 r
n
H (a − r) > −1
1
k
a
n+1
J
n+1
(ak)
20 r
n
exp (−ar), (Re a>0) > −1
1
√
π
2
n+1
Γ
(
n+
3
2
)
ak
n
(a
2
+k
2
)
n+
3
2
21 r
n
exp
−ar
2
> −1
k
n
(2a)
n+1
exp
−
k
2
4a
15.5 Hankel Transforms 693
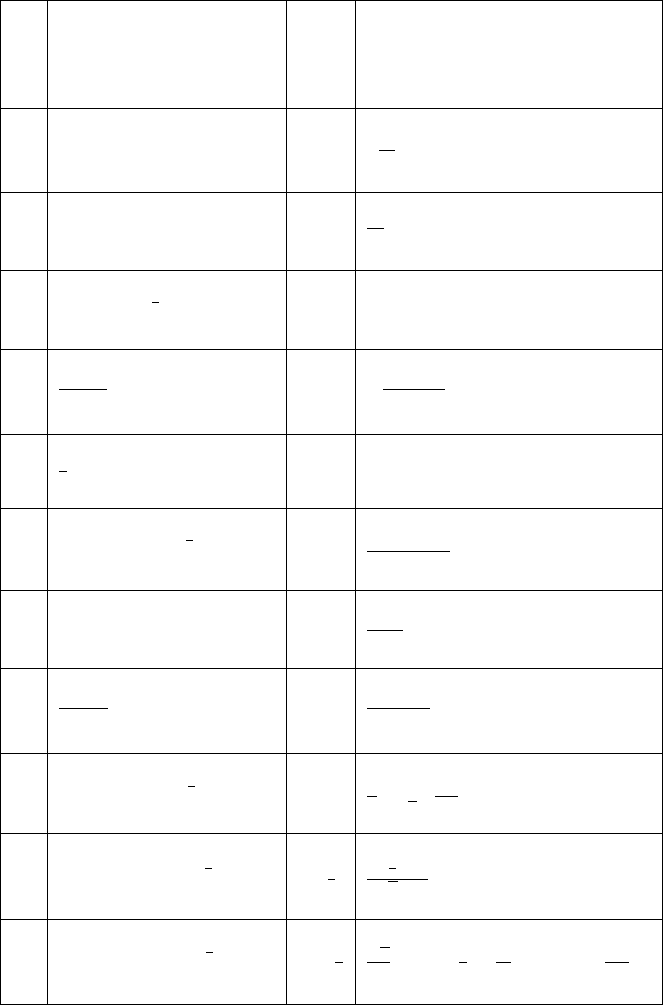
f (r) order
n
˜
f
n
(k)=
∞
0
rJ
n
(kr) f (r) dr
22 r
a−1
> −1
2aΓ
[
1
2
(a+n+1)
]
k
a+1
Γ
[
1
2
(1−a+n)
]
23 r
n
a
2
− r
2
m−n−1
×H (a − r)
> −1 2
m−n−1
Γ (m − n) a
m
k
n−m
J
m
(ak)
24 r
m
exp
−r
2
/a
2
> −1
k
n
a
m+n+2
2
n+1
Γ (n+1)
Γ
1+
m
2
+
n
2
×
1
F
1
1+
m
2
+
n
2
; n +1; −
1
4
a
2
k
2
25
1
r
J
n+1
(ar)
> −1 k
n
a
−(n+1)
H (a − k), a>0
26 r
n
a
2
− r
2
m
H (a − r),
m>−1
> −1 2
m
a
n
Γ (m +1)
a
k
m+1
×J
n+m+1
(ak)
27
1
r
2
J
n
(ar)
>
1
2
⎧
⎨
⎩
1
2n
k
a
n
, 0 <k≤ a
1
2n
a
k
n
,a<k<∞
28
r
n
(a
2
+r
2
)
m+1
, a>0
> −1
k
2
m
a
n−m
Γ (m+1)
K
n−m
(ak)
29 exp
−p
2
r
2
J
n
(ar) > −1
2p
2
−1
exp
−
a
2
+k
2
4p
2
I
n
ak
2p
2
30
1
r
exp (−ar)
> −1
(
k
2
+a
2
)
1
2
−a
n
k
n
(k
2
+a
2
)
1
2
31
r
n
(r
2
+a
2
)
n+1
> −1
k
2
n
K
0
(ak)
Γ (n+1)

694 15 Tables of Integral Transforms
f (r) order
n
˜
f
n
(k)=
∞
0
rJ
n
(kr) f (r) dr
32
r
n
(a
2
−r
2
)
n+
1
2
H (a − r)
< 1
1
√
π
k
2
n
Γ
1
2
− n
sin ak
k
33 f (ar) n
1
a
2
˜
f
n
k
a
34 r
−1
exp
−ar
2
1
1
k
"
1 − exp
−
k
2
4a
#
35 r
−1
sin
ar
2
,a>0
1
1
k
sin
k
2
4a
36 r
−1
cos
ar
2
,a>0
1 1 − cos
k
2
4a
37 exp (−ar) ,a>0 > −1
(
a+n
√
k
2
+a
2
)
(k
2
+a
2
)
3/2
k
a+
√
a
2
+k
2
n
38 exp
−ar
2
J
0
(br) 0
a
2
exp
−
k
2
−b
2
4a
I
0
bk
2a
39
H(a−r)
√
a
2
−r
2
0
aπ
2k
J
1
2
(ak) ,a>0
40
r
n
H(a−r)
√
a
2
−r
2
> −1
π
2k
a
n+
1
2
J
n+1
(ak) ,a>0
41 r
−2
sin r 0 sin
−1
1
k
, (k>1)
15.6 Finite Hankel Transforms 695
15.6 Finite Hankel Transforms
f (r) order
n
˜
f
n
(k
i
)=
a
0
rJ
n
(rk
i
) f (r) dr
1 c, where c is a constant 0
ac
k
i
J
1
(ak
i
)
2
a
2
− r
2
0
4a
k
3
i
J
1
(ak
i
)
3
a
2
− r
2
−
1
2
0 k
−1
i
sin (ak
i
)
4
J
0
(αr)
J
0
(αa)
0 −
ak
i
(
α
2
−k
2
i
)
J
1
(ak
i
)
5
1
r
1 k
−1
i
{1 − J
0
(ak
i
)}
6 r
−1
a
2
− r
2
−
1
2
1
(1−cos ak
i
)
(ak
i
)
7 r
n
> −1
a
n+1
k
i
J
n+1
(ak
i
)
8
J
ν
(αr)
J
ν
(αa)
> −1
ak
i
(
α
2
−k
2
i
)
J
′
ν
(ak
i
)
9 r
−n
a
2
− r
2
−
1
2
> −1
π
2
&
J
n
2
ak
i
2
'
2
10 r
n
a
2
− r
2
−
(
n+
1
2
)
<
1
2
Γ
(
1
2
−n
)
√
π 2
n
k
n−1
i
sin (ak
i
)
11 r
n−1
a
2
− r
2
n−
1
2
> −
1
2
√
π
2
Γ
n +
1
2
2
k
i
n
a
2n
J
2
n
ak
i
2
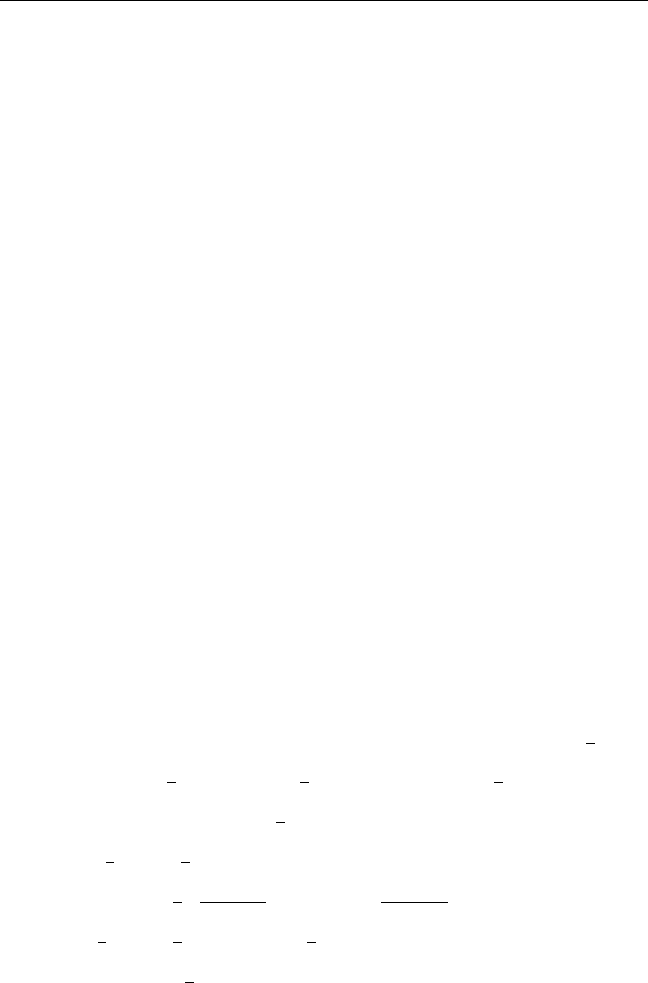
Answers and Hints to Selected Exercises
1.6 Exercises
1. (a) Linear, nonhomogeneous, second-order; (b) qu asi-linear, first-order;
(c) nonlinear, first-order; (d) linear, homogeneous, fourth-order; (e) lin-
ear, nonhomogeneous, second-order; (f) quasi-linear, third -order; (g)
nonlinear, second-order; and (h) nonlinear, homogeneous.
5. u (x, y)=f (x)cosy + g (x)siny.
6. u (x, y)=f (x) e
−y
+ g (y).
7. u (x, y)=f (x + y)+g (3x + y).
8. u (x, y)=f (y + x)+g (y − x).
11. u
x
= v
y
⇒ u
xx
= v
xy
, v
x
= −u
y
⇒ v
yx
= −u
yy
.
Thus, u
xx
+ u
yy
= 0. Similarly, v
xx
+ v
yy
=0.
12. Since u (x, y) is a homogeneous function of degree n, u = x
n
f
y
x
.
u
x
= nx
n−1
f
y
x
− x
n−2
yf
′
y
x
,andu
y
= x
n−1
f
′
y
x
.
Thus, xu
x
+ yu
y
= nx
n
f
y
x
= nu.
23. u
x
= −
1
b
exp
−
x
b
f (ax − by)
+exp
−
x
b
d
d(ax−by )
f (ax − by) ·
d(ax−by )
dx
= −
1
b
exp
−
x
b
f + a exp
−
x
b
f
′
(ax − by)
u
y
=(−b)exp
−
x
b
f
′
(ax − by) . Thus, bu
x
+ au
y
+ u =0.
698 Answers and H ints to Selected Exercises
24. V
′′
(t)+2bV
′
(t)+k
2
c
2
V (t)=0.
25. Differentiating with respect to r and t partially gives
V
′′
(r)+n
2
V (r)=0.
2.8 Exercises
2. (a) xp − yq = x − y,(d)yp − xq = y
2
− x
2
.
3. (a) u = f (y), (b) u = f (bx − ay), (c) u = f (ye
−x
),
(d) u = f
y − tan
−1
x
,(e)u = f
x
2
−y
2
x
,
(f) Hint:
dx
y +u
=
dy
y
=
du
x−y
=
d(x+u)
x+u
=
d(u+y)
x
, xdx=(u + y) d (u + y) ⇒
(u + y)
2
− x
2
= c
1
.
d(u+x)
u+x
=
dy
y
⇒
u+x
y
= c
2
,
f
u+x
y
, (u + y)
2
− x
2
=0.
(g)
dx
y
2
=
dy
−xy
=
du
xu−2xy
=
d(u−y )
x(u−y)
.
From the second and the fourth, (u − y) y = c
1
and x
2
+ y
2
= c
2
.
Hence, (u − y) y = f
x
2
+ y
2
.Thus,u = y + y
−1
f
x
2
+ y
2
.
(h) u +logx = f (xy), (i) f
x
2
+ u
2
,y
3
+ u
3
=0.
4. u (x, y)=f
x
2
+ y
−1
. Verify by differentiation that u satisfies the
original equation.
5. (a) u =sin
x −
3
2
y
,(b)u =exp
x
2
− y
2
,
(c) u = xy + f
y
x
, u = xy +2−
y
x
3
,(d)u =sin
y −
1
2
x
2
,
(e) u =
⎧
⎪
⎨
⎪
⎩
1
2
y
2
+exp
−
x
2
− y
2
!
for x>y,
1
2
x
2
+exp
−
y
2
− x
2
!
for x<y.
(f) Hint: y =
1
2
x
2
+ C
1
, u = C
2
1
x + C
2
,
u = x
y −
1
2
x
2
2
+f
y −
1
2
x
2
, u = x
y −
1
2
x
2
2
+exp
y −
1
2
x
2
.
(g)
y
x
= C
1
and
u+1
y
= C
2
, C
2
=1+
1
C
2
1
.Thus, u = y +
x
2
y
− 1,
y =0.
(h) Hint: x + y = C
1
,
dy
−u
=
du
u
2
+C
2
1
, u
2
+ C
2
1
= C
2
exp (−2y).

2.8 Exercises 699
From the Cauchy data, it follows that 1 + C
2
1
= C
2
, and hence,
u =
"(
1+(x + y)
2
)
e
−2y
− (x + y)
2
#
1
2
.
(i)
dy
dx
−
y
x
=1,
d
dx
y
x
=
1
x
which implies that x = C
1
exp
y
x
.
u+1
x
= C
2
. Hence, f
u+1
x
,xexp
−
y
x
=0.
Initial data imply x = C
1
and
x
2
+1
x
= C
2
. Hence C
2
= C
1
+
1
C
1
.
u+1
x
= x exp
−
y
x
+
1
x
exp
y
x
.Thus,u = x
2
exp
−
y
x
+exp
y
x
− 1.
(j)
dx
√
x
=
dy
u
=
du
−u
2
. The second and the third give y = −log (Au)and
hence, A = 1 and u =exp(−y). The first and the third yield
u
−1
=2
√
x − B.At(x
0
, 0), x
0
> 0, B =2
√
x
0
− 1. Hence,
u
−1
=2
√
x −
√
x
0
+1=
1
y
. The solution along the characteristic is
u =exp(−y)oru
−1
=2
√
x −
√
x
0
+1.
(k)
dx
ux
2
=
dy
exp(−y )
=
du
−u
2
. The first and the third give x
−1
=logu + A
and hence, A =
1
x
0
, x
0
> 0. The second and third yield u =exp(−y).
Or, eliminating u gives y =
x
−1
0
− x
−1
.
6. u
2
− 2ut +2x = 0, and hence, u = t +
√
t
2
− 2x.
7. u (x, y)=exp
x
x
2
−y
2
.
8. (a) u = f
y
x
,
z
x
(b) Hint: u
1
=
x−y
xy
= C
1
,
d(x−y )
x
2
−y
2
=
dz
z(x+y)
gives u =
x−z
z
= C
2
. Hence, u = f
x−y
xy
,
x−y
z
.
(c) φ =(x + y + z)=C
1
.
Hint:
(
dx
x
)
y −z
=
(
dy
y
)
z−x
=
(
dz
z
)
x−y
=
dx
x
+
dy
y
+
dz
z
0
=
d log(xyz)
0
,
ψ = xyz = C
2
, and hence, u = f (x + y + z, xyz) is the general
solution.
(d) Hint: xdx+ ydy=0,x
2
+ y
2
= C
1
zdz = −
x
2
+ y
2
ydy= −C
1
ydy, z
2
+
x
2
+ y
2
y
2
= C
2
,
u = f
x
2
+ y
2
,z
2
+
x
2
+ y
2
y
2
.
(e)
x
−1
dx
y
2
−z
2
=
y
−1
dy
z
2
−x
2
=
z
−1
dz
y
2
−x
2
=
d(log xyz)
0
. u = f
x
2
+ y
2
+ z
2
,xyz
.
700 Answers and H ints to Selected Exercises
9. (a) Hint: y −
x
2
2
= C
1
, u = xy −
x
3
3
+ C
2
,φ
u − xy +
x
3
3
,y−
x
2
2
=0.
u = xy −
x
3
3
+ f
y −
x
2
2
, u = xy −
x
3
3
+
y −
x
2
2
2
.
(b) u = xy −
1
3
x
3
+ y −
x
2
2
+
5
6
.
11.
x+u
y
= C
1
, u
2
− (x − y)
2
= C
2
, u
2
−
2u
y
− (x − y)
2
−
2
y
(x − y)=0.
u =
2
y
+(x − y), y>0.
12. (a) x =
τ
2
2
+ τs + s, y = τ +2s, u = τ + s =
(
2x−2y+y
2
)
2(y−1)
(b) x =
τ
2
2
+ τs + s
2
, y = τ +2s, u = τ + s,
(y − s)
2
=2x − s
2
, which is a set of parabolas.
(c) x =
1
2
(τ + s)
2
, y = u = τ + s.
13. Hint: The initial curve is a characteristic, and hence, no solution exists.
14. (a) u =exp
xy
x+y
,(b)u =sin
x
2
−y
2
+1
2
1
2
,
(c) u =2
xy
3
1
2
+
1
2
log
y
3x
,(e)u =
1
2
x
2
−
1
4
y
2
+
1
2
x
2
y +
1
4
.
(f) Hint:
dx
1
=
dy
2
=
du
1+u
, y − 2x = c
1
and (1 + u) e
−x
= c
2
,
(1 + u) e
−x
= f (y − 2x), 1+u =exp(3x − y +1)[1+sin(y − 2x − 1)].
(g) Hint:
dx
1
=
dy
2
=
du
u
, y−2x = c
1
,andue
−x
= c
2
, ue
−x
= f (y − 2x),
u =exp
y −x
2
cos
y −3x
2
.
(h)
dx
1
=
dy
2x
=
du
2xu
,(y − x)
2
= c
1
,andue
−x
2
= c
2
, ue
−x
2
=
f
y − x
2
, u (x, y)=
x
2
− y
e
y
.
(i)
dx
u
=
dy
1
=
du
u
, u − x = c
1
,andue
−y
= c
2
, f (ue
−y
,u− x)=0,
ue
y
= g (u − x), u =
2xe
y
2e
y
−1
,
dx
dy
= u, x = A (2e
y
− 1) is the family of
characteristics.
(j)
dx
1
=
dy
1
=
du
u
2
, y − x = c
1
,and
1
u
+ x = c
2
,
1
u
+ x = f (y − x),
f (x)=−
1−tanh x
tanh x
, u (x , y)=
tanh(x−y)
1−y tanh(x−y)
.
15. 3uy = u
2
+ x
2
+ y
2
.Hint:
xdx+ydy+udu
0
, x
2
+ y
2
+ u
2
= c
1
,
dy
y
= −
du
u
gives uy = c
2
.
x
2
+ y
2
+ u
2
= f (uy), and hence, 3u
2
= f
u
2
.
