Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


6.14 Exercises 721
π
x
a
cos πt −
1
πt
dt =ln
sin πx
πx
− ln
sin πa
πa
=
∞
n=1
ln
n
2
− x
2
n
2
− a
2
.
In the limit as a → 0, we find
ln
sin πx
πx
=
∞
n=1
ln
1 −
x
2
n
2
,
or
sin πx = πx
∞
3
n=1
1 −
x
2
n
2
.
This is the product representation of sin πx.
(d) Putting x =
1
2
, we obtain the Wallis formula for
π
2
as an infinite
product
π
2
=
∞
3
n=1
(2n)
2
(2n − 1) (2n +1)
=
2
1
·
2
3
·
4
3
·
4
5
·
6
5
·
6
7
·
8
7
···· .
36. (a) f (x +2π)=f (x).
a
k
=
1
π
2π
0
e
x
cos kx dx, b
k
=
1
π
2π
0
e
x
sin kx dx.
Evaluating these integrals gives
f (x) ∼
1
π
e
2π
− 1
1
2
+
∞
k=1
1
(k
2
+1)
(cos kx − k sin kx)
.
(b) In this case, f (−x)=−f (x)andf (x) is odd, and periodic of
period 2π.
Hence, a
k
=0,andb
k
is given by
b
k
=
2
π
π/2
0
sin kx dx −
2
π
π
π
2
sin kx dx.
Thus,
f (x)=
4
π
sin 2x +
1
3
sin 6x +
1
5
sin 10x + ...
.
(c) f (x) is periodic with period 1. Hence,
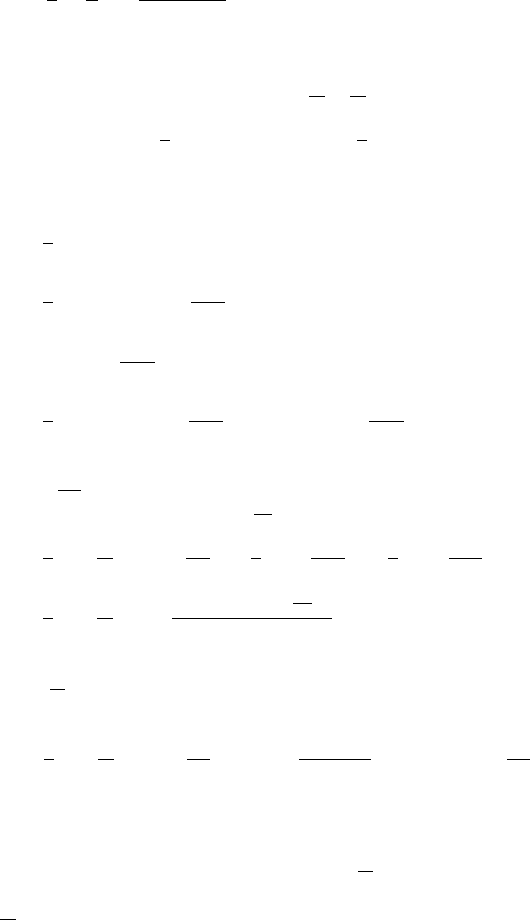
722 Answers and H ints to Selected Exercises
a
k
=2
1
0
f (x) cos (2πkx) dx, b
k
=2
1
0
f (x)sin(2πkx) dx,
f (x) ∼
1
2
−
1
π
∞
k=1
sin (2πkx)
k
,x= k.
f (x) = 0 for all x = k, and the corresponding infinite series does not
represent the value 0 of f (x)forx =0,+
1, + 2, ....Thus,
1
2
[f (n+) + f (n−)] =
1
2
.
37. (a) This represents a square wave function.
a
0
=
1
l
l
−l
f (x) dx =
l
0
dx = l,
a
k
=
1
l
l
−l
f (x)cos
πkx
l
dx
=
l
0
cos
πkx
l
dx =0,k=0.
b
k
=
1
l
l
−l
f (x)sin
πkx
l
dx =
l
0
sin
πkx
l
dx
=
l
πk
(1 − cos πk)=
⎧
⎨
⎩
0,kis even,
2l
πk
,kis odd.
f (x)=
l
2
+
2l
π
sin
πx
l
+
1
3
sin
3πx
l
+
1
5
sin
5πx
l
+ ...
=
l
2
+
2l
π
∞
k=1
sin
(2k − 1)
πx
l
!
(2k − 1)
.
At x =0,+
nl, f is not continuous, all terms in the above series after
the first vanish and the sum is (l/2). The graphs of the partial sums
s
n
(x)=
l
2
+
2l
π
sin
πx
l
+ ...+
1
(2n − 1)
sin
(
(2n − 1)
πx
l
)
can be drawn. These graphs show how the Fourier series converges at
the points of continuity of f (x), s
n
(x) → f (x)asn →∞. However,
at points of discontinuity at x = 0 and x =+
l, s
n
(x)doesnotcon-
verge to the mean value. Just beyond the discontinuities at x = 0 and
x =+
l, the partial sums, s
n
(x) overshoot the value |l|. This behavior
of the Fourier series at points of discontinuity is known as the Gibbs
phenomenon.
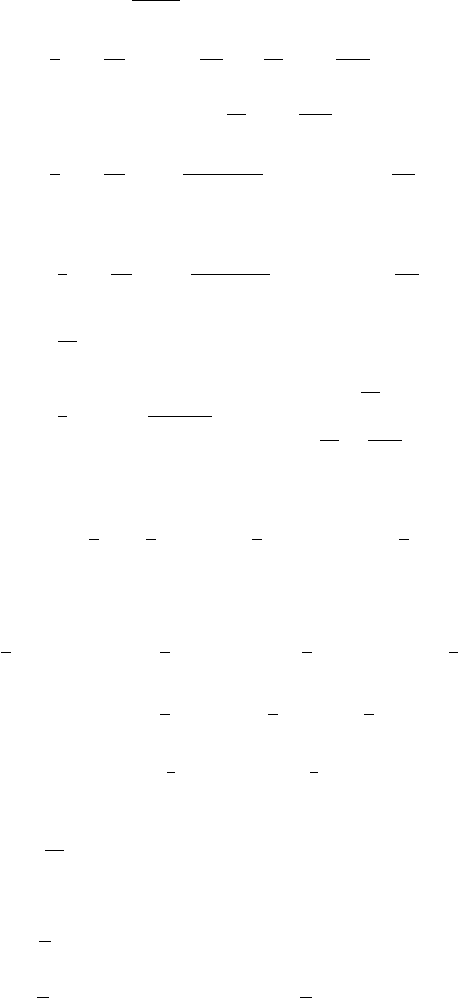
6.14 Exercises 723
(b) a
0
= l, a
k
=
2l
(πk)
2
(cos kπ − 1) ,b
k
=0,k=1, 2,....
f (x)=
l
2
−
4l
π
2
cos
πx
l
+
1
3
2
cos
3πx
l
+
1
5
2
cos
5πx
l
+ ...
=
l
2
−
4l
π
2
∞
k=1
1
(2k − 1)
2
cos
(
(2k − 1)
πx
l
)
.
(c) f (x)=
l
2
+
4l
π
2
∞
k=1
1
(2k − 1)
2
cos
"
(2k − 1)
πx
l
#
.
(d) f (x)=
a
0
2
+
∞
k=1
[a
k
cos (πkx)+b
k
sin (πkx)] ,
a
0
=
l
3
,a
k
=
2(−1)
k
π
2
k
2
,b
k
=
⎧
⎨
⎩
−
1
πk
,kis even,
1
πk
−
4
π
3
k
3
,kis odd.
38. (a) We have
cos kx sin
1
2
x =
1
2
sin
k +
1
2
x − sin
k −
1
2
x
.
Summing from k =1tok = n gives
sin
1
2
x
n
k=1
cos kx =
1
2
n
k=1
sin
k +
1
2
x − sin
k −
1
2
x
=
1
2
sin
n +
1
2
x − sin
1
2
x
Dividing this result by sin
1
2
x and adding
1
2
to both sides gives the
result.
(b) s
n
(x)=
a
0
2
+
n
k=1
(a
k
cos kx + b
k
sin kx) , where
(a
k
cos kx + b
k
sin kx)
=
1
π
π
−π
f (t)coskt dt
cos kx
+
1
π
π
−π
f (t)sinkt dt
sin kx =
1
π
π
−π
f (t)cosk (t − x) dt.
Thus,

724 Answers and H ints to Selected Exercises
a
0
2
=
1
2π
π
−π
f (t) dt and hence,
s
n
(x)=
a
0
2
+
n
k=1
(a
k
cos kx + b
k
sin kx)
=
1
2π
π
−π
f (t) dt +
1
π
n
k=1
π
−π
f (t)cosk (t − x) dt
=
1
π
π
−π
f (t)
1
2
+
n
k=1
cos k (t − x)
dt
=
1
π
π
−π
f (t)
sin
&
n +
1
2
(t − x)
'
2sin
1
2
(t − x)
dt from (a)
which is, from t − x = ξ,
=
1
π
π −x
−π−x
f (x + ξ)
sin
n +
1
2
ξ
2sin
1
2
ξ
dξ,
since the integrand has a period of 2π , we can replace the interval−π−x,
π−x by any interval of length 2π,thatis,(−π, π). This gives the result.
7.9 Exercises
1. (a) u (x, t)=
∞
n=1
4
(nπ )
3
[1 − (−1)
n
] cos (nπct)sin(nπx).
(b) u (x, t)=3cosct sin x.
2. (a) u (x, t)=
∞
n=1,3,4,...
32[(−1)
n
−1]
πcn
2
(n
2
−4)
sin (nct)sin(nx).
5. u (x, t)=
∞
n=1
a
n
T
n
(t)sin
nπx
l
,wherea
n
=
2
l
l
0
f (x)sin
nπx
l
dx, and
T
n
(t)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
e
−at/2
cosh αt +
a
2α
sinh αt
, for α
2
> 0
e
−at/2
1+
at
2
, for α =0
e
−at/2
cos βt +
a
2β
sin βt
, for α
2
< 0,
in which
α =
1
2
"
a
2
− 4
b +
n
2
π
2
c
2
l
2
#
1
2
,β=
1
2
"
4
b +
n
2
π
2
c
2
l
2
− a
2
#
1
2
.
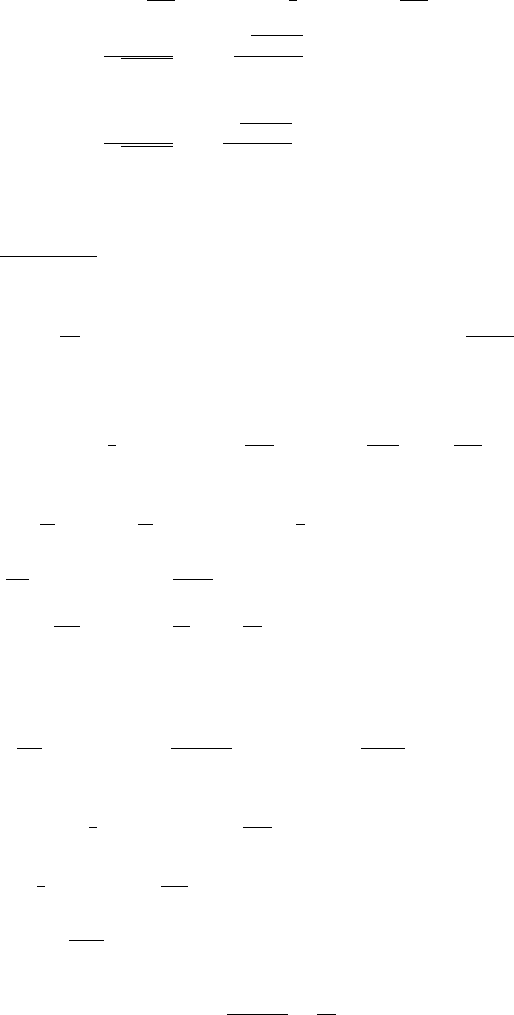
7.9 Exercises 725
6. u (x, t)=
∞
n=1
a
n
T
n
(t)sin
nπx
l
, a
n
=
2
l
l
0
g (x)sin
nπx
l
dx,and
T
n
(t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
2e
−at/2
√
(a
2
−α)
sinh
√
(a
2
−α)
2
t
, for a
2
>α,
te
−at/2
, for a
2
= α,
2e
−at/2
√
(α−a
2
)
sin
√
(α−a
2
)
2
t
, for a
2
<α.
7. θ (x, t)=
∞
n=1
a
n
cos (aα
n
t)sin(α
n
x + φ
n
), where
a
n
=
2
(
α
2
n
+h
2
)
2h+(α
2
n
+h
2
)l
l
0
f (x)sin(α
n
x + φ
n
) dx
and
φ
n
= tan
−1
α
n
h
; α
n
are the roots of the equation tan αl =
2hα
α
2
−h
2
.
11. u (x, t)=v (x, t)+U (x), where
v (x, t)=
∞
n=1
−
2
l
l
0
U (τ )sin
nπτ
l
dτ
cos
nπc t
l
sin
nπx
l
and
U (x)=−
A
c
2
sinh x +
A
c
2
sinh (l + k − h)
x
l
+ h.
12. u (x, t)=
A
6c
2
x
2
(1 − x)+
∞
n=1
12
(nπ )
3
(−1)
n
cos (nπct)sin(nπx).
14. (a) u (x, t)=−
hx
2
2k
+
2u
0
+
h
2k
x −
4h
kπ
e
−kπ
2
t
sin (πx)
+
∞
n=2
a
n
e
−kn
2
π
2
t
sin (nπx),
where
a
n
=
2u
0
nπ
[1 + (−1)
n
]+
2u
0
n
(n
2
−1)π
[1 + (−1)
n
]+
2h
kπ
3
n
3
[(−1)
n
− 1].
(b) Hint: v (x, t)=e
−ht
u (x , t).
u (x , t)=e
−ht
1
2
a
0
+
∞
n=1
a
n
cos
nπx
l
exp
−n
2
π
2
kt/l
2
,where
a
n
=
2
l
l
0
f (ξ)cos
nπξ
l
dξ.
15. (a) u (x, t)=
∞
n=1
4
n
3
π
3
"
2(−1)
n+1
− 1
#
e
−4n
2
π
2
t
sin (nπx).
(b) u (x, t)=
∞
n=1,3,4,...
[(−1)
n
− 1]
"
n
π (4−n
2
)
−
1
nπ
#
e
−n
2
kt
sin (nx).

726 Answers and H ints to Selected Exercises
16. u (x, t)=
∞
n=1
2l
2
n
3
π
3
[1 − (−1)
n
] e
−(nπ /l)
2
t
cos
nπx
l
.
18. v (x, t)=Ct
1 −
x
l
−
Cl
2
6k
"
x
l
3
− 3
x
l
2
+2
x
l
#
+
2Cl
2
π
3
k
∞
k=1
e
−n
2
π
2
kt/l
2
n
3
sin
nπx
l
.
21. u (x, t)=v (x, t)+w (x), where
v (x, t)=e
−kt
sin x +
∞
n=1
a
n
e
−n
2
kt
sin (nx), and
a
n
=
−n
(n
2
+a
2
)
[(−1) e
−n−ax
− 1] +
2A
a
2
kπ
1
n
{(−1)
n
− 1}
!
+
(−1)
n
n
[e
−aπ
− 1]
w (x)=
A
a
2
k
1 − e
−ax
+
x
π
(e
−aπ
− 1)
!
.
36. Hint: Suppose R is the rectangle 0 ≤ x ≤ a,0≤ y ≤ b and ∂R is
its boundary positively oriented. Suppose that u
1
and u
2
are solutions
of the problem, and put v =(u
1
− u
2
). Then v satisfies the Laplace
equation with v =(x, 0) = 0 = v (x, b), v
x
(0,y)=0=v
x
(a, y).
8.14 Exercises
1. (a) λ
n
= n
2
, φ
n
(x)=sinnx for n =1, 2, 3,...
(b) λ
n
= ((2n − 1) /2)
2
, φ
n
(x) = sin ((2n − 1) /2) πx for n =1, 2, 3,...
(c) λ
n
= n
2
, φ
n
(x)=cosnx for n =1, 2, 3,....
2. (a) λ
n
=0,n
2
π
2
, φ
n
(x)=1,sinnπx,cosnπx for n =1, 2, 3,...
(b) λ
n
=0,n
2
, φ
n
(x)=1,sinnx,cosnx for n =1, 2, 3,...
(c) λ
n
=0,4n
2
, φ
n
(x)=1,sin2nx, cos 2nx for n =1, 2, 3,....
3. (a) λ
n
= −
3/4+n
2
π
2
, φ
n
(x)=e
−x/2
sin nπx, n =1, 2, 3,....
4. (a) λ
n
=1+n
2
π
2
, φ
n
(x)=(1/x)sin(nπ ln x), n =1, 2, 3,....
(b) λ
n
=
1
4
+(nπ/ ln 3)
2
, φ
n
(x)=
"
1/ (x +2)
1
2
#
sin [(nπ/ ln 3) ln (x + 2)],
n =1, 2, 3,....

9.10 Exercises 727
(c) λ
n
=
1
12
"
1+(2nπ/ ln 2)
2
#
,
φ
n
(x)=
"
1/ (1 + x)
1
2
#
sin [(nπ/ ln 2) ln (1 + x)], n =1, 2, 3,....
5. (a) φ (x)=sin
√
λ ln x
, λ>0.
(b) φ (x)=sin
√
λx
, λ>0.
7. f (x) ∼
∞
n=1
2
π
"
(−1)
n
−1
n
2
#
cos nx.
11. (a) G (x, ξ)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
x, x ≤ ξ
ξ, x > ξ.
12. (a) u (x)=−cos x +
cos 1−1
sin 1
sin x +1,
(b) u (x)=−
2
5
cos 2x −
1
10
1+2 sin 2
cos 2
sin 2x +
1
5
e
x
.
16. G (x, ξ)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
x
3
ξ/2
+
xξ
3
/2
− (9xξ/5) + x, for 0 ≤ x<ξ
x
3
ξ/2
+
xξ
3
/2
− (9xξ/5) + ξ, for ξ ≤ x ≤ 1.
24. (a) Hint: Differentiate cot θ =
py
′
y
with respect to x to find
−cosec
2
θ
dθ
dx
=
1
y
(py
′
)
′
−
1
y
2
py
′2
= −
λr + q +
1
p
cot
2
θ
.
dθ
dx
=(q + λr)sin
2
θ +
1
p
cos
2
θ,
dr
dx
=
r
2
1
p
− q − λr
sin 2θ.
(b) At θ = nπ,
dθ
dx
=
1
p
,andatθ =
n +
1
2
π,
dθ
dx
=(q + λp).
9.10 Exercises
8. (a) u (r, θ)=
4
3
1
r
−
r
4
sin θ.
(c) u (r, θ)=
∞
n=1
a
n
sinh
(nπ/ ln 3)
θ −
π
2
!
sin [(nπ/ ln 3) ln r],
where
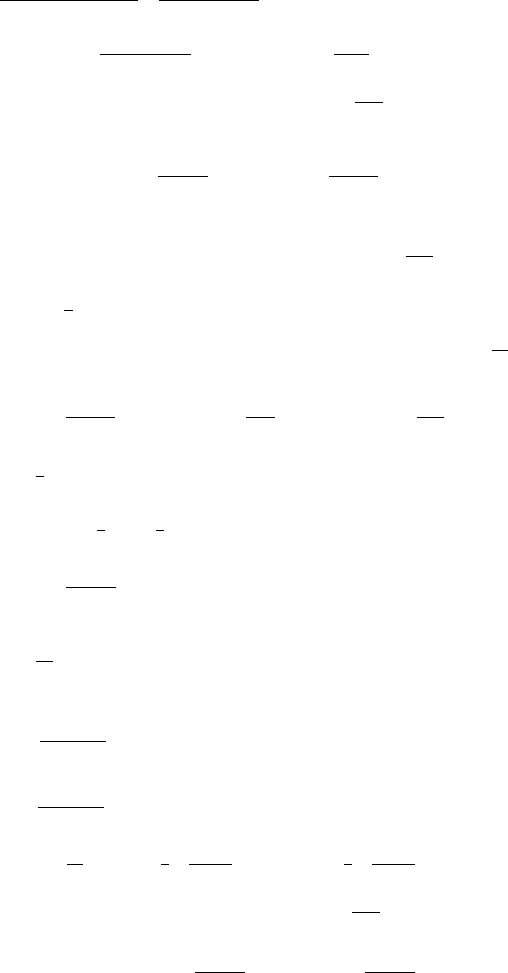
728 Answers and H ints to Selected Exercises
a
n
=
2
ln 3 sinh(nπ
2
/2ln3)
(
nπ ln 3
n
2
π
2
+4(ln 3)
2
[9 (−1)
n
− 1]
−
4nπ ln 3
n
2
π
2
+(ln 3)
2
[3 (−1)
n
− 1] +
3ln3
nπ
[(−1)
n
− 1]
)
.
9. u (r, θ)=
∞
n=1
a
n
r
−nπ /α
− b
−2nπ /α
r
nπ /α
sin
nπθ
α
+
∞
n=1
b
n
sinh
"
nπ
ln(b/a)
(θ − α)
#
sin
"
nπ
ln(b/a)
(ln r − ln a)
#
,
where
a
n
=2
α
a
−nπ /α
− b
−2nπ /α
a
nπ /α
!
−1
α
0
f (θ)sin
nπθ
α
dθ,
b
n
= −2
ln
b
a
sinh {αnπ/ ln (b/a)}
!
−1
+
b
a
f (r) sin [(nπ/ ln [b/a]) ln (ra)]
dr
r
.
12. u (r, θ)=
∞
n=1
2
αJ
ν
(a)
α
0
f (θ)sin
nπτ
α
dτ
J
ν
(r)sin
nπθ
α
, ν = nπ/α.
13. u (r, θ)=
1
2
a
2
− r
2
.
14. (a) u (r, θ)=−
1
3
r +
4
r
sin θ + constant.
16. u (r, θ)=
∞
n=1
1
nR
n−1
r
n
sin nθ.
18. u (r, θ)=
a
0
2
+
∞
n=1
r
n
(a
n
cos nθ + b
n
sin nθ),
where
a
n
=
R
1−n
(n+Rh)π
2π
0
f (θ)cosnθ dθ, n =0, 1, 2,....
b
n
=
R
1−n
(n+Rh)π
2π
0
f (θ)sinnθ dθ, n =1, 2, 3,....
20. u (r, θ)=c −
r
4
12
sin 2θ +
1
6
r
6
1
−r
6
2
r
4
1
−r
4
2
r
2
sin 2θ +
1
6
r
2
1
−r
2
2
r
4
1
−r
4
2
r
4
1
r
4
2
r
−2
sin 2θ.
21. u (r, θ)=
∞
n=1
a
n
r
−nπ /α
− b
−2nπ /α
r
nπ /α
sin
nπθ
α
+
∞
n=1
b
n
sinh
"
nπ
ln(b/a)
(θ − α)
#
sin
"
nπ
ln(b/a)
(ln r − ln a)
#
.
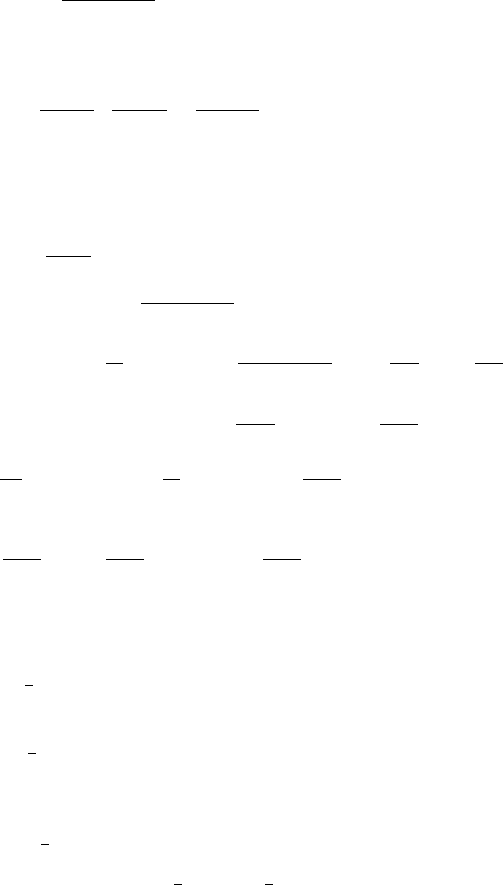
9.10 Exercises 729
22. (a) u (x, y)=
∞
n=1
4[1−(−1)
n
]
(nπ )
3
sinh nπ
sin nπx sinh {nπ (y − 1)}
(c) u (x, y)=
∞
n=1
a
n
(sinh nπx − tanh nπ cosh nπx)sinnπy,where
a
n
=
1
tanh nπ
"
2nπ
3
n
2
π
4
−4
+
1−(−1)
n
nπ
#
.
23. (a) u (x, y)=c +
∞
n=1
a
n
(cosh nx − tanh nπ sinh nx)cosny,where
a
n
=2[1− (−1)
n
]
=
n
3
π tanh nπ
.
(c) u (x, y)=−
1
tanh π
[cosh y − tanh π sinh y]cosx + C.
25. u (x, y)=xy (1 − x)+
∞
n=1
4(−1)
n
(nπ )
3
sinh nπ
sin (nπx)sinh(nπy).
27. u (x, y)=c +
x
2
/2
x
2
3
− y
2
+
∞
n=1
8a
4
(−1)
n+1
(nπ )
3
sinh nπ
cosh
nπx
a
cos
nπy
a
.
29. u (x, y)=x [(x/2) − π]+
∞
n=1
a
n
sin
&
2n−1
2
x
'
cosh
&
2n−1
2
y
'
,where
a
n
=
2
Aπ
π
0
"
f (x) − h
x
2
2
− πx
#
sin
2n−1
2
x
!
dx
with
A =
2n−1
2
sinh
2n−1
2
π + h cosh
2n−1
2
π.
32. Hint: The solution is given by (9.5.3) and the boundary conditions re-
quire
sin
2
θ =
1
2
a
0
+
∞
n=1
[(a
n
+ b
n
)cosnθ +(c
n
+ d
n
)sinnθ] ,
0=
1
4
b
0
+
∞
n=1
n
a
n
2
n−1
− b
n
2
−n−1
cos nθ
+
c
n
2
n−1
− d
n
2
−n−1
sin nθ
!
.
Using sin
2
θ =
1
2
(1 − cos 2θ), we equate coefficients to obtain
a
0
=1, b
0
=0; a
2
+ b
2
= −
1
2
,2a
2
−
1
8
b
2
=0;
a
n
+ b
n
=0
2
n−1
a
n
− 2
−n−1
b
n
=0
⎫
⎪
⎬
⎪
⎭
n =1, 3, 4, 5,....
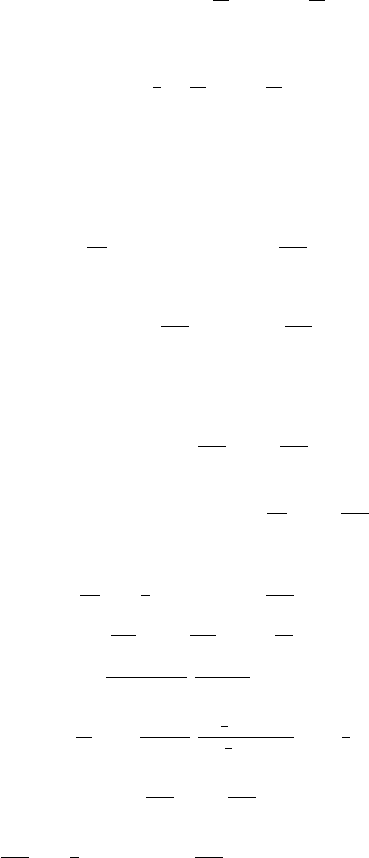
730 Answers and H ints to Selected Exercises
c
n
+ d
n
=0
2
n−1
c
n
− 2
−n−1
d
n
=0
⎫
⎪
⎬
⎪
⎭
n =1, 2, 3,....
Thus, a
0
=1,b
0
=1,a
2
= −
1
34
, b
2
= −
8
17
, and the remaining coeffi-
cients are zero; finally
u (r, θ)=
1
2
−
1
34
r
2
+
16
r
2
cos 2θ.
33. (a) Hint: Seek a separable solution u (r, z)=R (r) Z (z)sothat
r
2
R
′′
+ rR
′
− λr
2
R =0,andZ
′′
+ λZ =0,withZ (0) = 0 = Z (h).
The solution of this eigenvalue problem is
λ
n
=
nπ
h
2
,Z
n
(z)=sin
nπz
h
,n=1, 2, 3,....
The solution of the radial equation is
R
n
(r)=a
n
I
0
nπr
h
+ b
n
K
0
nπr
h
,
where I
0
and K
0
are modified Bessel functions. Since K
0
is unbounded
at r =0,allb
n
≡ 0. Thus,
u (r, z)=
∞
n=1
a
n
I
0
nπr
h
sin
nπz
h
.
f (z)=u (1,z)=
∞
n=1
a
n
I
0
nπ
h
sin
nπz
h
.
This is a Fourier sine series for f (z) and hence,
a
n
I
0
nπ
h
=
2
h
h
0
f (z)sin
nπz
h
dz.
(d) u (r, z)=aI
0
3πr
h
sin
3πz
h
=
I
0
3π
h
.
35. (a) u (r, z)=8
∞
n=1
sinh zk
n
zk
n
sinh k
n
J
0
(k
n
r)
J
0
(k
n
)
.
(b) u (r, z)=
4a
π
∞
n=1
1
(2n−1)
I
0
[
1
2
(2n−1)r
]
I
0
[
1
2
(2n−1)
]
sin
&
1
2
(2n − 1) z
'
.
(c) u (r, z)=
∞
n=1
a
n
I
0
nπr
h
sin
nπz
h
,where
a
n
I
0
nπa
h
=
2
h
h
0
f (z)sin
nπz
h
dz.
