Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

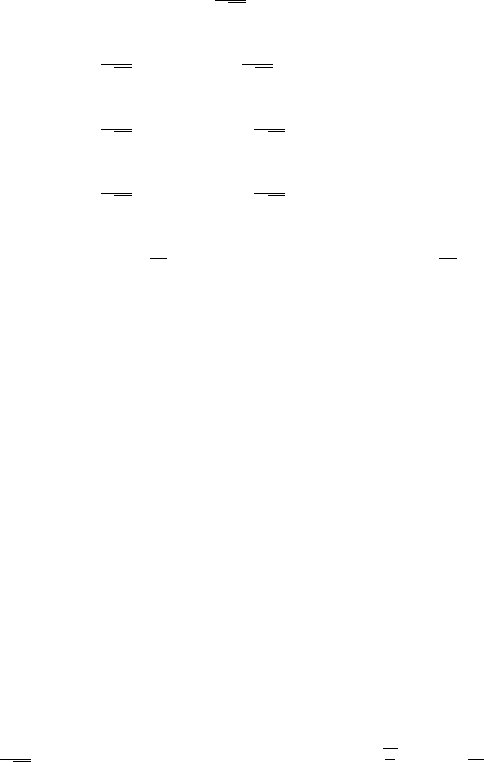
12.18 Exercises 741
=
∞
−∞
∞
−∞
f (x − t − η) g (η) dη
h (t) dt
=
∞
−∞
(f ∗g)(x − t) h (t) dt =[(f ∗ g) ∗ h](t).
(g) F
−1
{(F ∗ G)(k)} =
1
√
2π
∞
−∞
e
ikx
[F (k) ∗ G (k)] dk
=
1
√
2π
∞
−∞
e
ikx
dk
1
√
2π
∞
−∞
F (k − ξ) G (ξ) dξ
=
1
√
2π
∞
−∞
G (ξ) dξ
1
√
2π
∞
−∞
e
ikx
F (k − ξ) dk
=
1
√
2π
∞
−∞
G (ξ) dξ
1
√
2π
∞
−∞
e
i(ξ+η)x
F (η) dη = f (x) g (x).
9. (a) (f ∗g)
′
(x)=
d
dx
∞
−∞
f (x − ξ) g (ξ) dξ =
∞
−∞
d
dx
f (x − ξ)
!
g (ξ) dξ
=
∞
−∞
f
′
(x − ξ) g (ξ) dξ =(f
′
∗ g)(x).
(c) Apply the Fourier transform and then use the convolution theorem.
The use of the inverse Fourier transform proves the r esult.
(d)
∞
−∞
(f ∗g)(x) dx =
∞
−∞
∞
−∞
f (x − ξ) g (ξ) dξ
dx
=
∞
−∞
g (ξ)
∞
−∞
f (x − ξ) dx
dξ
=
∞
−∞
g (ξ)
∞
−∞
f (η) dη
dξ
=
∞
−∞
g (ξ) dξ
∞
−∞
f (η) dη.
(f) Apply the definition of the Fourier transform without the factor
1
√
2π
. This means that F
&
exp
−ax
2
'
=
π
a
exp
−
k
2
4a
.
F{(G
t
∗ G
s
)(x)} = F{G
t
(x)}F{G
s
(x)}
=exp
−k
2
κt
exp
−k
2
κs
.
=exp
−k
2
(t + s) κ
!
.
The inverse Fourier transform gives the result.
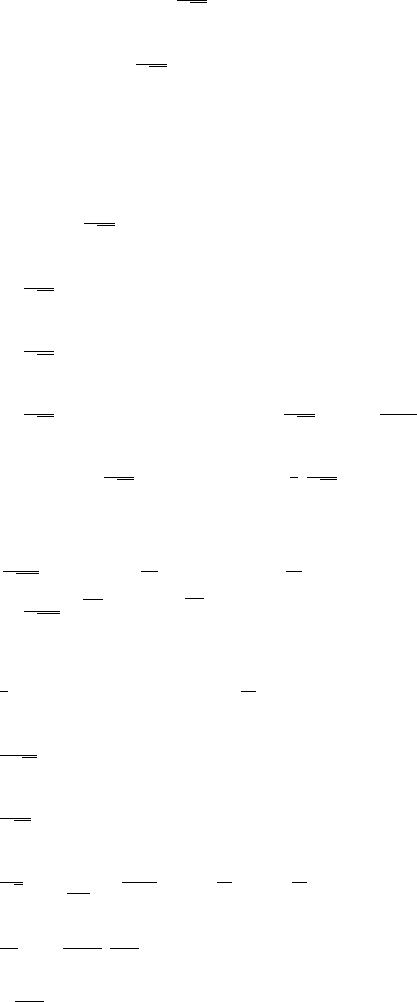
742 Answers and H ints to Selected Exercises
10. (b) L.H.S. =
∞
−∞
g (k) e
ikx
dk
1
√
2π
∞
−∞
e
−iky
f (y) dy
=
∞
−∞
f (y) dy
1
√
2π
∞
−∞
e
−ik(y−x)
g (k) dk
=
∞
−∞
G (y − x) f (y) dy.
(c) Putting x = 0 in the result of 10(b) gives the desired result.
(d) sin x ∗ e
−a|x|
=
1
√
2π
∞
−∞
sin (x − ξ) e
−a|ξ|
dξ
=
1
√
2π
∞
0
sin (x + η) e
−aη
dη +
∞
0
sin (x − ξ) e
−aξ
dξ
=
1
√
2π
∞
0
[sin (x + ξ)+sin(x − ξ) ] e
−aξ
dξ
=
1
√
2π
2sinx
∞
0
cos ξe
−aξ
dξ =
1
√
2π
sin x
a
1+a
2
.
(e) e
ax
∗ χ
[0,∞)
(x)=
1
√
2π
∞
0
e
a(x−ξ)
dξ =
1
a
e
ax
√
2π
.
(f) Apply the Fourier transform to the left hand side to obtain
1
√
4ab
F
(
exp
−
x
2
4a
)
F
(
exp
−
x
2
4b
)
=
1
√
4ab
√
2ae
−ak
2
·
√
2be
−bk
2
= e
−(a+b)k
2
which can be inverted to find the result.
11. u (x, t)=
1
2
[f (x + ct)+f (x − ct)] +
1
2c
x+ct
x−ct
g (τ) dτ .
12. u (x, t)=
1
2
√
πt
∞
0
"
e
−(x−ξ)
2
/4t
− e
−(x+ξ)
2
/4
#
f (ξ) dξ.
13. u (x, t)=
1
√
2π
∞
−∞
F (ξ)cos
cξ
2
t
e
−iξx
dξ.
14. u (x, t)=
1
√
π
∞
x/
√
2at
g
t−x
2
2aξ
2
sin
ξ
2
2
+cos
ξ
2
2
dξ.
15. u (x, t)=
δ
0
2π
∞
−∞
sin aξ
ξ
e
iξx
|ξ|
e
−|ξ|y
dξ.
16. φ (x, t)=
√
4πt
∞
−∞
e
−(x−ξ)
2
/4t
f (ξ) dξ.
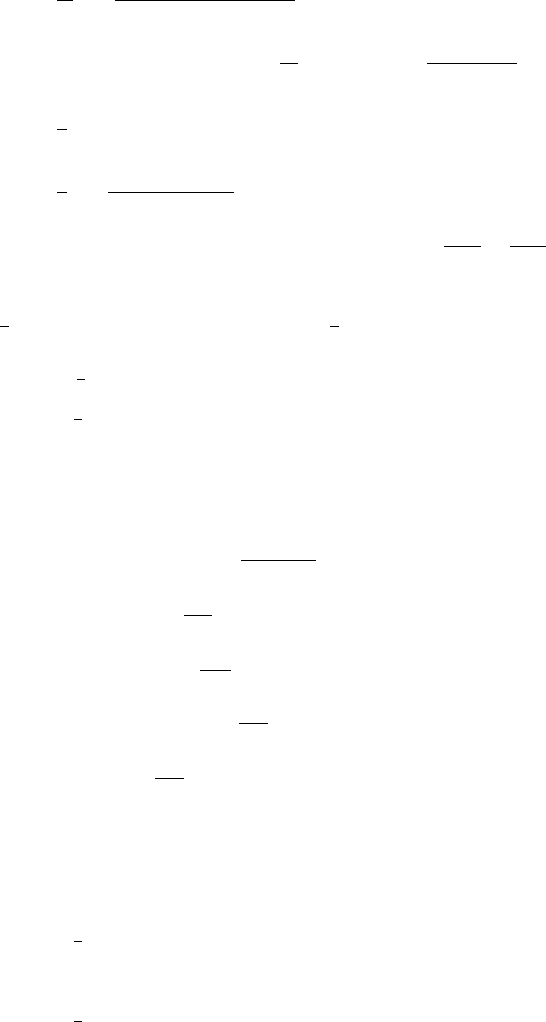
12.18 Exercises 743
19. u (x, y)=
2y
π
∞
0
(
x
2
+τ
2
+y
2
)
f(τ )dτ
[
y
2
+(x−τ)
2
][
y
2
+(x+τ)
2
]
−
1
2π
∞
0
g (τ)log
[
x
2
+(y +τ )
2
]
[
x
2
+(y −τ )
2
]
dτ.
21. u (x, y)=
2
π
∞
0
ξ sin xξ
t
0
e
−ξ
2
(t−τ)
f (τ) dτ dξ.
22. u (x, y)=
2
π
∞
0
sin ξx sin hξ(1−y)
sin hξ
∞
0
f (τ)sinξτ dτ dξ.
24. (a)
b
2
− a
2
−1
(cos at − cos bt), (b)
b
2
− a
2
−1
sin at
a
−
sin bt
b
,
(c) (a − b)
−1
e
at
− e
bt
,(d)1− e
−at
− ate
−at
,
(e)
1
a
(1 − e
−at
), (f)
1
a
sin at − 2(sinat ∗ sin at).
28. u (x, t)=
⎧
⎪
⎨
⎪
⎩
1
2
[f (ct + x) − f (ct − x)] f or t>x/c
1
2
[f (x + ct)+f (x − ct)] for t<x/c.
29. u (x, t)=
⎧
⎪
⎨
⎪
⎩
0, for t<x/c
f (t − x/c) , for x/c<t≤ (2 − x) /c.
30. u (x, t)=f
0
+(f
1
− f
0
)erfc
(x
2
/4κt)
.
31. u (x, t)=x − x erfc
x/
√
4κt
.
32. u (x, t)=2
t
0
η
0
erfc
x/
√
4κξ
dη dξ.
33. u (x, t)=f
0
e
−ht
1 − erfc
x/
√
4κt
!
.
34. u (x, t)=f
0
erfc
x/
√
4κt
.
35. u (x, t)=
⎧
⎪
⎨
⎪
⎩
f
0
t, for t<x/c
f
0
x/c, for t>x/c.
36. u (x, t)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
1
2
[f (x + ct) − f (ct − x)] ,t<x/c
1
2
[f (x + ct)+f (x − ct)] , t > x/c.
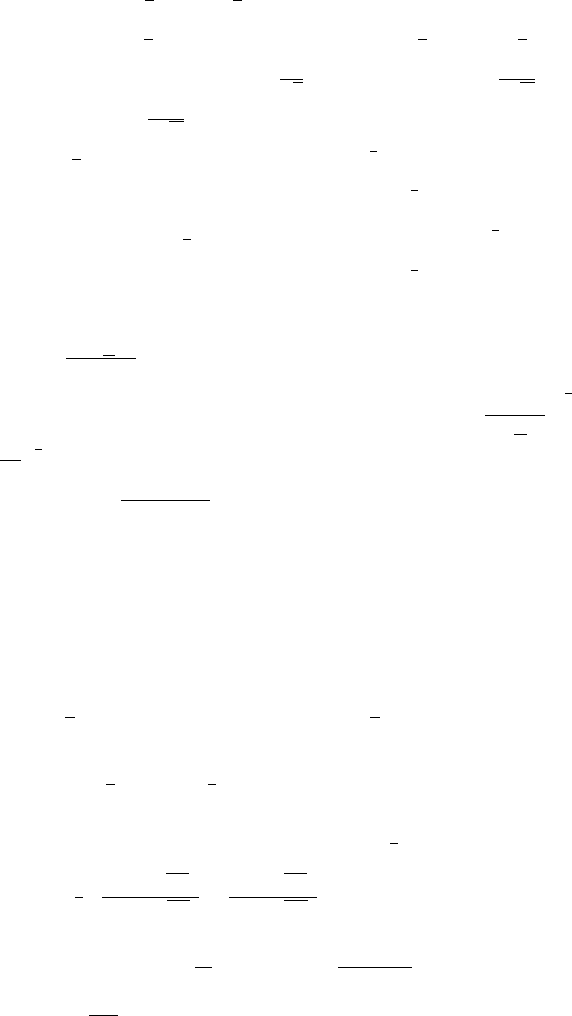
744 Answers and H ints to Selected Exercises
37. V (x, t)=V
0
t −
x
c
H
t −
x
c
.
(i) V = V
0
H
t −
x
c
, (ii) V = V
0
cos
&
ω
t −
x
c
'
H
t −
x
c
.
38. u (z, t)=Ut
"
1+2ζ
2
erfc (ζ) −
2ζ
√
π
e
−ζ
2
#
,where ζ =
z
2
√
νt
.
41. V (x, t)=V
0
erfc
x
2
√
κt
.
42. q (z, t)=
a
2
e
iω t
"
e
−λ
1
z
erfc
(
ζ − [it (2Ω + ω)]
1
2
)
+e
λ
1
z
erfc
(
ζ +[it (2Ω + ω)]
1
2
)#
+
b
2
e
−iω t
"
e
−λ
2
z
erfc
(
ζ − [it (2Ω − ω)]
1
2
)
+e
λ
2
z
erfc
(
ζ +[it (2Ω − ω)]
1
2
)#
,
where
λ
1,2
=
i
(
2Ω +
ω
)
ν
.
q (z,t) ∼ a exp (iωt − λ
1
z)+b exp (−iωt − λ
2
z), δ
1,2
=
ν
|
2Ω +
ω
|
1
2
.
43.
ν
2Ω
1
2
.
45. f (t)=f (0) +
1
Γ (α)Γ (1−α)
t
0
g (x)(t − x)
α−1
dx.
46. x = a (θ − sin θ), y = a (1 − cos θ).
55. u (x, t)=
∞
n=1
sin nx
t
0
e
−n
2
(t−τ)
a
n
(τ) dτ +
∞
n=1
b
n
(0) sin nx e
−n
2
t
,
where
a
n
(t)=
2
π
π
0
g (x, t)sinnx dx, b
n
(0) =
2
π
π
0
f (x)sinnx dx.
57. u (x, t)=
∞
n=1
2
π
sin
&
n −
1
2
x
'
t
0
π
0
e
−(2n−1)
2
(t−τ)/4
×sin
&
n −
1
2
ξ
'
g (ξ,τ ) dξ dτ.
61. u (x, t)=
c
2
sinh
x
√
1/c
sinh
π
√
1/c
−
sin
x
√
1/c
sin
π
√
1/c
sin t
+
2
πc
∞
n=1
(−1)
n+1
n
n
4
−(1/c)
2
sin n
2
ct sin nx,
in which
1/c is not an integer.

14.11 Exercises 745
65. f (x)=
∞
0
g (t) h (xt) dt,whereh (x)=M
−1
"
1
K(1−p)
#
.
14.11 Exercises
13. (c) With h =0.2, the initial values are u
i,0
(ih, 0) = sin π (ih).
u
1,0
=sin0.2π =0.5878, u
2,0
=sin0.4π =0.9511.
Also, u
2,0
= u
3,0
and u
1,0
= u
4,0
.
In each time step, there are 4 internal mesh points. We have to solve
4 equations with 4 unknowns. However, the initial temperature distri-
bution is symmetric about x =0.5, and u = 0 at the endpoints for all
time t.Wehaveu
3,1
= u
2,1
and u
4,1
= u
1,1
in the first time row and
similarly for the other time rows. This gives two equations with two
unknowns.
16. (a) y = x
3
,(b)y =sinx,(c)x
2
+(y − β)
2
= r
2
,
where β and r are constants.
17. x = a (θ − sin θ), y = a (1 − cos θ).
18. Hint: I (y (x)) = 2π
x
1
x
0
y
1+y
′2
1
2
dx.
x = c
1
t + c
2
, y = c
1
cosh t = c
1
cosh
x−c
2
c
1
.
(A surface generated by rotation of a catenary is called a catenoid ).
21. (a) ∇
4
u = 0 (Biharmonic equation)
(b) u
tt
− α
2
∇
2
u + β
2
u = 0 (Klein–Gordon equation)
(c) φ
t
+ αφ
x
+ βφ
xxx
=0,(φ = u
x
) (KdV equation)
(d) u
tt
+ α
2
u
xxxx
= 0 (Elastic beam equation)
(e)
d
dx
(pu
′
)+(r + λs) u = 0 (Sturm–Liouville equation).
22.
2
2m
∇
2
ψ +(E − V ) ψ =0 (Schr¨odinger equation).
24. u
tt
− c
2
u
xx
= F (x, t), where c
2
= T
∗
/ρ.
746 Answers and H ints to Selected Exercises
29. Hint: y
n
= x (1 − x)
n
r=1
a
r
x
r−1
. Find the solution for n = 1 and n =2.
n =1: a
1
=
5
18
, y
1
= a
1
x (1 − x).
n =2: a
1
=
71
369
, a
2
=
7
41
, y
2
= x (1 − x)(a
1
+ a
2
x).
30. Hint: u
1
(x, y)=a
1
xy.
I (u
1
)=
πab
4
"
(a
1
+1)
2
a
2
+(a
1
− 1)
2
b
2
#
, a
1
=
b
2
−a
2
b
2
+a
2
.
31. Hint: u
3
= x (1 − x)(1− y)+x (1 − x) y (1 − y)(a
2
+ a
3
y).
32. Hint: u
2
= x (2 − x − 2y)+a
2
xy (2 − x − 2y).
33. Hint: Ψ
N
=
N
m,n=1
a
mn
φ
mn
=
N
m,n=1
a
mn
cos
mπ x
2a
cos
nπy
2b
.
34. Hint: φ
n
=cos
(2n − 1)
πr
2a
!
.
35. Hint: I (u)=
a
−a
a
−a
"
∇
2
u
2
−
4α
a
2
u
#
dx dy =min,and
u
n
=
x
2
− a
2
2
y
2
− a
2
2
a
1
+ a
2
x
2
+ a
3
y
3
+ ...
.
36. Hint: Ψ
1
=
b
2
− y
2
U (x).
37. (a) Introduce two functions φ and ψ and two parameters α and β such
that U = u + αφ (x)andV = v + βψ (x). Then
∂I
∂α
= 0 and
∂I
∂β
=0.
40. (a) u
y
− u
x
y
′
=
uy
′′
1+y
′2
.
(b) y
′2
=
1−A
2
(y
1
−y )
A
2
(y
1
−y )
,(d)2y
′′
− 3y +3xy
2
=0.
42. Seek an approximate solution
u
n
(x, y)=
a
2
− x
2
b
2
− y
2
a
1
+ a
2
x
2
+ a
3
y
2
+ ...+ a
n
x
2r
y
2s
.
For n =1,f =2
0=
R
(−u
1xx
− u
1yy
− 2)
a
2
− x
2
b
2
− y
2
dx dy
=2
a
−a
b
−b
1 − a
1
a
2
− x
2
− a
1
b
2
− y
2
!
a
2
− x
2
b
2
− y
2
dx dy
=
32
9
a
2
b
3
−
128
45
(ab)
3
a
2
+ b
2
a
1
,a
1
=
5
4
a
2
+ b
2
−1
and u
1
=
5
4
(
a
2
−x
2
)(
b
2
−y
2
)
(a
2
+b
2
)
.

14.11 Exercises 747
The torsional moment
M =2Gθ
a
−a
b
−b
u
1
dx dy =
40
9
(Gθ)
a
3
b
3
a
2
+b
2
,
where G is the shear modulus and θ is the angle of twist per unit length.
When a = b, M =
20
9
Gθa
4
∼ 0.1388 (2a)
4
Gθ. The tangential stresses
are
τ
zx
= Gθ
∂u
1
∂y
,τ
zy
= Gθ
∂u
1
∂x
.
(b) The exact solution is
u (x , y)=x (a − x) −
8a
2
π
3
∞
n=1
cosh
{
(2n−1)
πy
2a
}
sin
{
(2n−1)
πx
a
}
(2n−1)
3
cosh
{
(2n−1)
πb
2a
}
.
M =2Gθ
a
3
b
6
−
32a
4
π
5
∞
n=1
1
(2n−1)
5
tanh
&
(2n − 1)
πb
2a
'
.
For a = b, M =0.1406 (2a)
4
Gθ.
43. This problem deals with the expansion of a rectangular plate under
tensile forces. Make the boundary conditions homogeneous. Integrating
the boundary conditions gives
u
0
=
1
2
cy
2
1 −
y
2
6b
2
.
Set u = u
0
+5u so that ∇
4
5u =
2c
b
2
and the boundary conditions become
5u
xy
=0=5u
yy
for x =+
a, 5u
xy
=0=5u
xx
for y =+b.
These boundary conditions hold if
5u =0, 5u
x
=0 for x =+
a,
5u =0, 5u
y
=0 for y =+
b.
By the Rayleigh–Ritz method
R
∇
4
u
n
− f
φ
k
dx dy =0,k=1, 2,...,n,
where the nth approximate solution u
n
(x, y) has the form
u
n
(x, y)=
x
2
− a
2
2
y
2
− b
2
2
a
1
+ a
2
x
2
+ a
3
y
2
+ ...
.
For n =1,
0=
a
−a
b
−b
24a
1
y
2
− b
2
2
+16a
1
3x
2
− a
2
3y
2
− b
2
+24a
1
x
2
− a
2
2
−
2c
b
#
x
2
− a
2
2
y
2
− b
2
2
dx dy,
748 Answers and H ints to Selected Exercises
or
54
7
+
256
49
b
2
a
2
+
64
7
b
4
a
4
a
1
=
c
a
6
b
2
.
When a = b, a
1
=(0.04325)
c
a
6
.
u
1
∼ u
0
+ 5u
1
=
1
2
cy
2
1 −
y
2
6b
2
+(0.04325)
ca
−6
×
x
2
− a
2
2
y
2
− b
2
2
.
44.
dF
dx
=
∂F
∂x
+
∂F
∂u
du
dx
+
∂F
∂u
′
·
du
′
dx
=
∂F
∂x
+ u
′
∂F
∂u
+ u
′′
∂F
∂u
′
d
dx
u
′
∂F
∂u
′
= u
′
d
dx
∂F
∂u
′
+
∂F
∂u
′
· u
′′
.
Subtracting the latter from the former with (14.6.12) we obtain
d
dx
F − u
′
∂F
∂u
′
=
∂F
∂x
+ u
′
∂F
∂u
−
d
dx
∂F
∂u
′
!
=
∂F
∂x
.
45. H = I − λJ =
b
a
F (x, y, y
′
) dx
=
b
0
p (x) y
′2
− q (x) y
2
− λr(x) y
2
!
dx.
The extremum of H leads to the Euler–Lagrange equation
d
dx
∂F
∂y
′
−
∂F
∂y
=0.
This leads to the answer.
46. (a) For simplicity, we assume that l is an integer and p artition the
interval into l equal subintervals. Each of the l −1=n interior vertices
has the trial function v
j
(x) defined by
v
j
(x)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
1 − j + x for j − 1 ≤ x ≤ j,
1+j − x for j ≤ x ≤ j +1,
0 otherwise.
v
j
(x) is continuous and piecewise linear with v
j
(j)=1andv
j
(k)=0
for all integers k = j.

Appendix: Some Special Functi ons and Their
Properties
“One of the properties inherent in mathematics is that any real progress is
accompanied by the discovery and development of new methods and sim-
plifications of previous procedures ... The unified character of mathematics
lies in its very nature; indeed, mathematics is the foundation of all exact
natural sciences.”
David Hilbert
This appendix is a short introduction to some special functions used in
the book. These functions include gamma, beta, error, and Airy functions
and their main properties. Also included are Hermite and Webber–Hermite
functions and their properties. Our discussion is brief since we assume that
the reader is already familiar with this material. For more details, the reader
is referred to appropriate books listed in the bibliography.
A-1 Gamma, Beta, Error, and Airy Functions
The Gamma function (also called the factorial function) is defined by a
definite integral in which a variable appears as a parameter
Γ (x)=
∞
0
e
−t
t
x−1
dt, x > 0. (A-1.1)
In view of the fact that the integral (A-1.1) is uniformly convergent for all
x in [a, b]where0<a≤ b<∞, Γ (x) is a continuous function for all x>0.
Integrating (A-1.1) by parts, we obtain the fundamental property of
Γ (x)
750 Appendix: Some Special Functions and Their Properties
Γ (x)=
−e
−t
t
x−1
!
∞
0
+(x − 1)
∞
0
e
−t
t
x−2
dt
=(x − 1) Γ (x − 1) , for x − 1 > 0.
Then we replace x by x + 1 to obtain the fundamental result
Γ (x +1)=xΓ(x) . (A-1.2)
In particular, when x = n is a positive integer, we make repeated use of
(A-1.2) to obtain
Γ (n +1)=nΓ (n)=n (n − 1) Γ (n − 1) = ···
= n (n − 1) (n − 2) ···3 · 2 · 1 Γ (1) = n!, (A-1.3)
where Γ (1) = 1.
We p ut t = u
2
in (A-1.1) to obtain
Γ (x)=2
∞
0
exp
−u
2
u
2x−1
du, x > 0. (A-1.4)
Letting x =
1
2
, we find
Γ
1
2
=2
∞
0
exp
−u
2
du =2
√
π
2
=
√
π. (A-1.5)
Using (A-1.2), we deduce
Γ
3
2
=
1
2
Γ
1
2
=
√
π
2
. (A-1.6)
Similarly, we can obtain the values of Γ
5
2
,Γ
7
2
,...,Γ
2n+1
2
.
The gamma function can also be defined for negative values of x by
rewriting (A-1.2) as
Γ (x)=
Γ (x +1)
x
,x=0, −1, −2,... (A-1.7)
For example
Γ
−
1
2
=
Γ
1
2
−
1
2
= −2 Γ
1
2
= −2
√
π, (A-1.8)
Γ
−
3
2
=
Γ
−
1
2
−
3
2
=
4
3
√
π. (A-1.9)
We differentiate (A-1.1) with respect to x to obtain
