Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

A-1 Gamma, Beta, Error, and Airy Functions 751
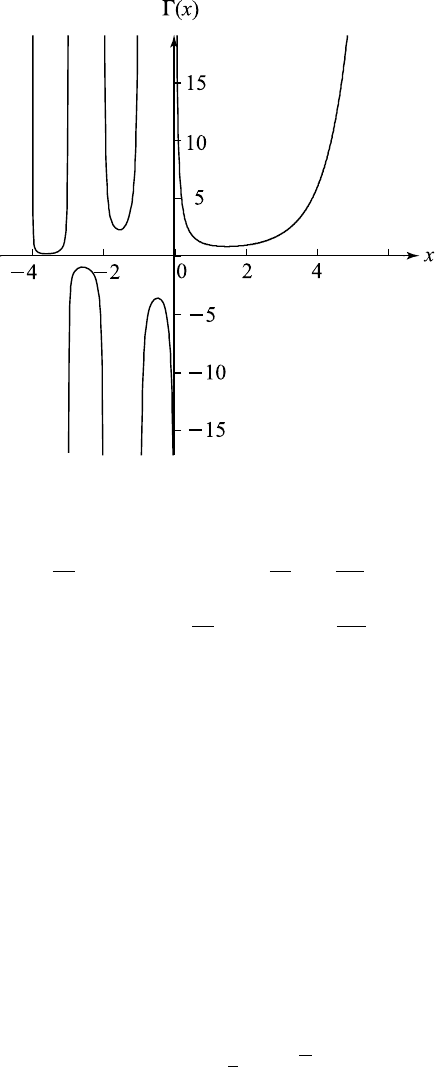
Figure A-1.1 The gamma function.
d
dx
Γ (x)=Γ
′
(x)=
∞
0
d
dx
(t
x
)
e
−t
t
dt
=
∞
0
d
dx
[exp (x log t)]
e
−t
t
dt
=
∞
0
t
x−1
(log t) e
−t
dt. (A-1.10)
At x =1,thisgives
Γ
′
(1) =
∞
0
e
−t
log tdt= −γ, (A-1.11)
where γ is called the Euler constant and has the value 0.5772.
The graph of the gamma function is shown in Figu re A-1.1.
Several u seful properties of the gamma function ar e recorded below
without proof for reference.
Legendre Duplication Formula
2
2x−1
Γ (x) Γ
x +
1
2
=
√
πΓ(2x) , (A-1.12)

752 Appendix: Some Special Functions and Their Properties
In particular, when x = n (n =0, 1, 2,...)
Γ
n +
1
2
=
√
π (2n)!
2
2n
n!
. (A-1.13)
The following properties also hold for Γ (x):
Γ (x) Γ (1 − x)=π cosec πx, x is a noninteger, (A-1.14)
Γ (x)=p
x
∞
0
exp (−pt) t
x−1
dt, (A-1.15)
Γ (x)=
∞
−∞
exp
xt − e
t
dt. (A-1.16)
Γ (x +1)∼
√
2π exp (−x) x
x+
1
2
for large x, (A-1.17)
n! ∼
√
2π exp (−n) x
n+
1
2
for large n. (A-1.18)
The incomplete gamma function, γ (x, a), is defined by the integral
γ (a, x)=
x
0
e
−t
t
a−1
dt, a > 0. (A-1.19)
The complementary incomplete gamma function, Γ (a, x), is defined by the
integral
Γ (a, x)=
∞
x
e
−t
t
a−1
dt, a > 0. (A-1.20)
Thus, it follows that
γ (a, x)+Γ (a, x)=Γ (a) . (A-1.21)
The beta function, denoted by B (x, y) is defined by the integral
B (x, y)=
t
0
t
x−1
(1 − t)
y −1
dt, x > 0,y>0. (A-1.22)
The beta function B (x, y)issymmetric with respect to its arguments
x and y,thatis,
B (x, y)=B (y, x) . (A-1.23)
This follows from (A-1.22) by the change of variable 1 − t = u,thatis,
B (x, y)=
1
0
u
y −1
(1 − u)
x−1
du = B (y, x) .
If we make the change of variable t = u /(1 + u) in (A-1.22), we obtain
another integral representation of the beta function
A-1 Gamma, Beta, Error, and Airy Functions 753
B (x, y)=
∞
0
u
x−1
(1 + u)
−(x+y )
du =
∞
0
u
y −1
(1 + u)
−(x+y )
du,
(A-1.24)
Putting t =cos
2
θ in (A-1.22), we derive
B (x, y)=2
π/2
0
cos
2x−1
θ sin
2y −1
θdθ. (A-1.25)
Several important results are recorded below without proof for ready
reference.
B (1, 1) = 1,B
1
2
,
1
2
= π, (A-1.26)
B (x, y)=
x − 1
x + y − 1
B (x − 1,y) , (A-1.27)
B (x, y)=
Γ (x) Γ (y)
Γ (x + y)
, (A-1.28)
B
1+x
2
,
1 − x
2
= π sec
πx
2
, 0 <x<1. (A-1.29)
The error function,erf(x) is defined by the integral
erf (x)=
2
√
π
x
0
exp
−t
2
dt, −∞ <x<∞. (A-1.30)
Clearly, it follows from (A-1.30) that
erf (−x)=−erf (x) , (A-1.31)
d
dx
[erf (x)] =
2
√
π
exp
−x
2
, (A-1.32)
erf (0) = 0, erf (∞)=1. (A-1.33)
The complementary error function,erfc(x) is defined by the integral
erfc (x)=
2
√
π
∞
x
exp
−t
2
dt. (A-1.34)
Clearly, it follows that
erfc (x)=1− erf (x) , (A-1.35)
erfc (0) = 1, erfc (∞)=0, (A-1.36)
erfc (x) ∼
1
x
√
π
exp
−x
2
for large x. (A-1.37)
The graphs of erf (x) and erfc (x) are shown in F igure A-1.2.
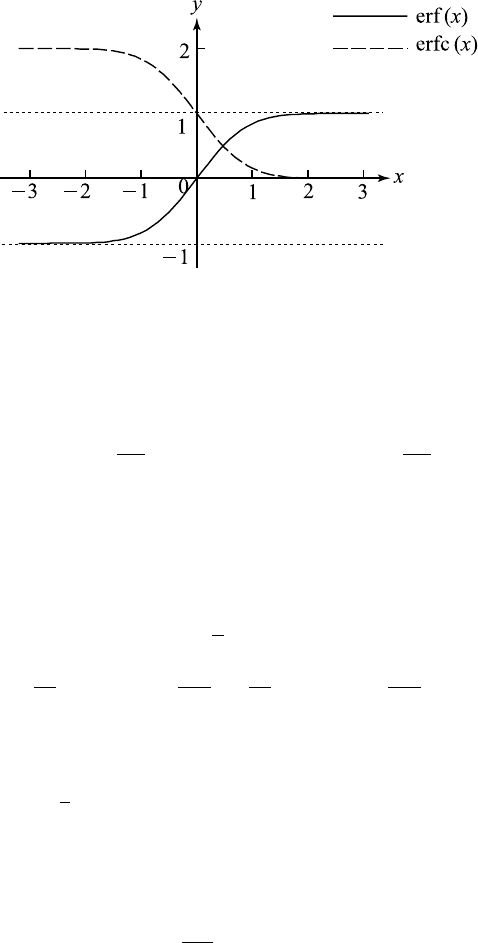
754 Appendix: Some Special Functions and Their Properties
Figure A-1.2 The error function and the complementary error function.
Closely associated with the error function are the Fresnel integrals,
which are defined by
C (x)=
x
0
cos
πt
2
2
dt and S (x)=
x
0
sin
πt
2
2
dt. (A-1.38)
These integrals arise in diffraction problems in optics, in water waves, in
elasticity, and elsewhere.
Clearly, it follows from (A-1.38) that
C (0) = 0 = S (0) (A-1.39)
C (∞)=S (∞)=
π
2
, (A-1.40)
d
dx
C (x)=cos
πx
2
2
,
d
dx
S (x)=sin
πx
2
2
. (A-1.41)
It also follows f rom (A-1.38) t hat C (x) has extrema at the points where
x
2
=(2n + 1), n =0, 1, 2, 3,..., and S (x) has extrema at the points where
x
2
=2n, n =1, 2, 3,.... The largest maxima occur first and are C (1) =
0.7799 and S
√
2
=0.7139. We also infer that both C (x)andS (x)are
oscillatory about the line y =0.5. The graphs of C (x)andS (x) for non-
negative real x are shown in Figure A-1.3.
The Airy different ial equation
d
2
y
dx
2
− xy = 0 (A-1.42)
has solutions y
1
= Ai (x)andy
2
= Bi(x) which are called Airy functions.
Using the t ransfor mation y (x)=x
α
f
x
β
,whereα and β are constants,
the Airy functions can be expressed in term of Bessel functions. Differenti-
ating y (x) with respect to x gives

A-1 Gamma, Beta, Error, and Airy Functions 755
Figure A-1.3 The Fresnel integrals C (x) and S (x).
y
′
(x)=αx
α−1
f + βx
α+β−1
f
′
,
y
′′
(x)=α (α − 1) x
α−2
f +
2αβ + β
2
− β
x
α+β−2
f
′
+ β
2
x
α+2β−2
f
′′
.
Substituting y and y
′′
into the Airy equation (A-1.42) gives
β
2
x
α+2β−2
f
′′
+
2αβ + β
2
− β
x
α+β−2
f
′
+ x
α−2
α (α − 1) − x
3
!
f =0.
Multiplying this equation by
x
2−α
β
−2
yields
x
2β
f
′′
+(2α + β − 1) β
−1
x
β
f
′
+ β
−2
α (α − 1) − x
3
!
f =0. (A-1.43)
Considering the coefficient of f, we require that x
3
be proportional to
x
2β
so that β =3/2. The coefficient of f
′
gives α =
1
2
. Hence, y (x)=
x
1
2
f
x
3/2
. Consequently, equation (A-1.43) becomes
x
3
f
′′
+ x
3/2
f
′
−
2
3
x
3/2
2
−
1
9
=0. (A-1.44)
This equation admits solutions in terms of Bessel functions K
1/3
(ξ)and
I
1/3
(ξ)whereξ =
2
3
x
3/2
. The general solution of the Airy equation in terms
of Bessel functions is given by
y (x)=
√
x
AK
1/3
(ξ)+BI
1/3
(ξ)
!
. (A-1.45)
In fact, the Airy functions can be expressed as
Ai (x)=
1
π
x
3
K
1/3
(ξ) , (A-1.46)
Bi(x)=
x
3
I
1/3
(ξ)+I
−1/3
(ξ)
!
. (A-1.47)
756 Appendix: Some Special Functions and Their Properties
The Airy equation (A-1.42) can also be solved by the method of Laplace,
that is, by seeking a solution in integral form
y (x)=
C
e
xz
u (z) dz, (A-1.48)
where the path of integration C is chosen such that u vanishes on the
boundary. It follows that u satisfies the first-order differential equation
du
dz
+ z
2
u =0.
The solution of this equation can be obtained in an integral form except
for a normalization factor as
y (x)=
1
2πi
i∞
−i∞
exp
xz −
1
3
z
3
dz = Ai (x) , (A-1.49)
or, equivalently,
Ai (x)=
1
2π
∞
−∞
exp
i
xz +
1
3
z
3
dz =
1
π
∞
0
cos
xz +
1
3
z
3
dz.
(A-1.50)
More generally,
Ai (ax)=
1
2πa
∞
−∞
exp
i
xz +
z
3
3a
3
dz
=
1
πa
∞
0
cos
xz +
z
3
3a
3
dz. (A-1.51)
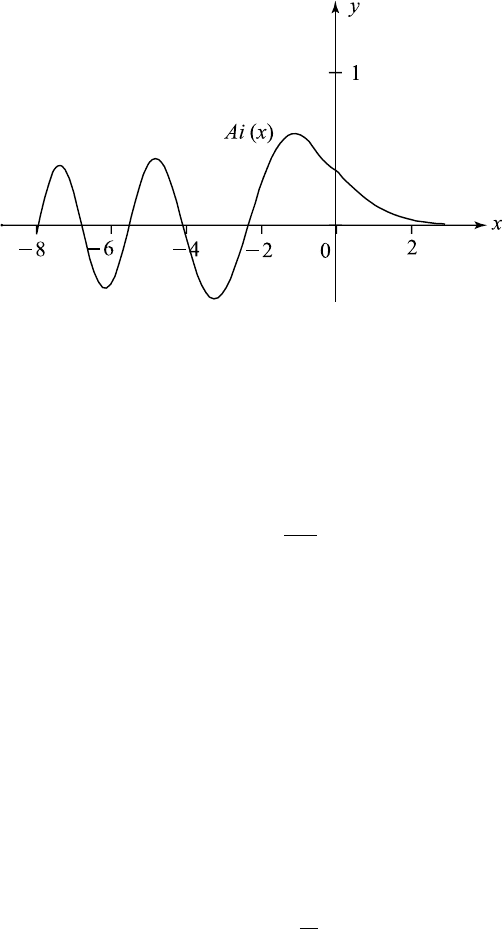
The graph of y = Ai (x) is shown in Figure A-1.4.
Finally, the method of power series can be used to solve the Airy equa-
tion to obtain the solution as
y (x)=a
0
1+
∞
n=1
x
3n
(3n)(3n − 1) (3n − 3) (3n − 4) ...3.2
+a
1
x +
∞
n=1
x
3n+1
(3n +1)(3n)(3n − 2) (3n − 3) ...4.3
, (A-1.52)
where a
0
and a
1
are constants.
The series solution (A-1.52) converges for all x rapidly due to the rapid
decay of the coefficients as n →∞.
A-2 Hermite Polynomials and Weber–Hermite Functions 757
Figure A-1.4 Graph of the Airy function.
A-2 Hermite Polynomials and Weber–Hermite
Functions
The Hermite polynomials H
n
(x) are defined by the Rodrigues formula
H
n
(x)=(−1)
n
exp
x
2
d
n
dx
n
exp
−x
2
!
, (A-2.1)
where n =0, 1, 2, 3,....
The first seven Hermite polynomials are
H
0
(x)=1
H
1
(x)=2x
H
2
(x)=4x
2
− 2
H
3
(x)=8x
3
− 12x
H
4
(x)=16x
4
− 48x
2
+12
H
5
(x)=32x
5
− 16x
3
+ 120x
H
6
(x)=64x
6
− 480x
4
+ 720x
2
− 120.
The generating function of H
n
(x)is
exp
2xt− t
2
=
∞
n=0
t
n
n!
H
n
(x) . (A-2.2)
It follows from (A-2.2) that H
n
(x) satisfies th e parity relation
H
n
(−x)=(−1)
n
H
n
(x) . (A-2.3)
Also, it follows from (A-2.2) that
758 Appendix: Some Special Functions and Their Properties
H
2n+1
(0) = 0,H
2n
(0) = (−1)
n
(2n)!
n!
. (A-2.4)
The recurrence relations for Hermite polynomials are
H
n+1
(x) − 2xH
n
(x)+2nH
n−1
(x)=0, (A-2.5)
H
′
n
(x)=2xH
n−1
(x) . (A-2.6)
The Hermite polynomials, y = H
n
(x), are solutions of the Hermite differ-
ential equation
y
′′
− 2xy
′
+2ny =0. (A-2.7)
The orthogonal property of Hermite polynomials is
∞
−∞
exp
−x
2
H
n
(x) H
m
(x) dx =2
n
n!
√
πδ
mn
. (A-2.8)
With repeated use of integration by parts, it follows from (A-2.1) that
∞
−∞
exp
−x
2
H
n
(x) x
m
dx =0,m=0, 1,...,(n − 1) , (A-2.9)
∞
−∞
exp
−x
2
H
n
(x) x
n
dx =
√
πn!. (A-2.10)
The Weber–Hermite or, simply the Hermite fu nction
y = h
n
(x)=exp
−
x
2
2
H
n
(x) (A-2.11)
satisfies the differential equation
h
′′
n
(x)+
λ − x
2
h
n
(x)=0, (A-2.12)
where λ =2n +1.If λ =2n +1, thenh
n
(x) is not finite as |x|→∞.
The Hermite functions {h
n
(x)}
∞
0
are an orthogonal basis for L
2
(R)
with weight function one. They satisfy the following relations:
h
′
n
(x)=−xh
n
(x)+2nh
n−1
(x) , (A-2.13)
h
′
n
(x)=xh
n
(x) − h
n+1
(x) , (A-2.14)
h
′′
n
(x) − x
2
h
n
(x)+(2n +1)h
n
(x)=0. (A-2.15)
The normalized Weber–Hermite functions are given by
ψ
n
(x)=
h
n
(x)
(2
n
n!
√
π)
exp
−
x
2
2
H
n
(x) . (A-2.16)
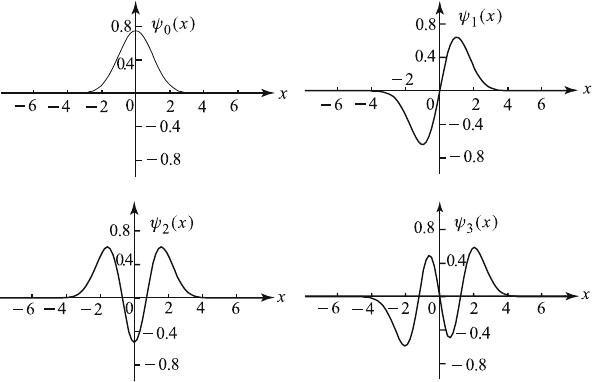
The functions {ψ
n
(x)} form a orthornormal set in (−∞, ∞), that is,
A-2 Hermite Polynomials and Weber–Hermite Functions 759
∞
−∞
ψ
m
(x) ψ
n
(x) dx = δ
mn
. (A-2.17)
Physically, they represent quantum mechanical oscillator wave functions.
Some graphs of these functions are shown in Figure A-2.1.
The Fourier transform of h
n
(x)is(−i)
n
h
n
(x), that is,
F{h
n
(x)} =(−i)
n
h
n
(x) . (A-2.18)
Figure A-2.1 The normalized Weber–Hermite functions.

Bibliography
The following bibliography is not, by any means, a complete on e for the
subject. For the most part, it consists of books and papers to which reference
is made in text. Many other selected books and papers related to material
in this book have been included so that they may serve to stimulate new
interest in future advanced study and research.
[1] Ablowitz, M.J. and Segur, H., Solitons and Inverse Scattering Trans-
form, SIAM, Philadelphia (1981).
[2] Arnold, V.I., Ordinary Differential Equations, Springer-Verlag, New
York (1992).
[3] Bateman, H., Partial Differential Equations of Mathematical
Physics, Cambridge University Press, Cambridge (1959).
[4] Becker, A.A., The Boundary Element Method in Engineering,Mc-
Graw Hill, New York (1992).
[5] Benjamin, T.B., Bona, J.L., and Mahony, J.J., Model equations for
long waves in nonlinear dispersive systems, Phil.Trans.Roy.Soc.
A272 (1972) 47–78.
[6] Berg, P. and McGregor, J., Elementary Partial Differential Equa-
tions, Holden-Day, New York (1966).
[7] Birkhoff, G. and Rota, G-C., Ordinary Differential Equations
(Fourth Edition), John Wiley and Sons, New York (1989).
[8] Boas, M.L., Mathematical Methods in the Physical Sciences, John
Wiley, New York (1966).
[9] Broman, A., Introduction to Partial Differential Equations: from
Fourier Series to Boundary-Value Problems, Addison-Wesley, Read-
ing, Massachusetts (1970).
[10] Brown, J.W. and Churchill, R.V., Fourier Series and Boundary
Value Problems (Fifth Edition), McGraw-Hill, New York (1993).
[11] Burgers, J.M., A mathematical model illustrating the theory of tur-
bulence, Adv. Appl. Mech. 1 (1948) 171–191.
[12] Byerly, W.E., Fourier Series, Dover Publications, New York (1959).
[13] Carleson, L. , On the convergence and growth of partial sums of
Fourier Series, Acta Mathematica, 116 (1966) 135–157.
[14] Carslaw, H.S., Introduction to the Theory of Fourier Series and In-
tegrals, Dover Publications, New York (1950).
