Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


4.6 Exercises 711
is u = φ (ξ)+ψ (η), where φ and ψ are arbitrary functions and the
transformation becomes ξ = x + by and η = x + dy,whereb, d are real
and distinct.
If B
2
−AC < 0, the equation i s elliptic, and b and d are complex conju-
gate numbers
d =
b
. With a = c = 1, the tr ansformation is given by
ξ = x+by and η = x+
by.Thenα =
1
2
(ξ + η)andβ =
1
2i
(ξ − η)canbe
used to transform the equation into the canonical form u
αα
+ u
ββ
=0.
If B
2
−AC = 0, the equation is parabolic, here b = −
B
C
, a, c and d are
arbitrary, b ut c and d are not b oth zero. Choose a = c =1,d =0so
that ξ = x −
B
C
y and η = y are used to transform the equation into the
form u
ηη
= 0. The general solution is u = φ (ξ)+ηψ (η), where φ and ψ
are arbitrary functions, and b isthedoublerootofCλ
2
+2Bλ+ A =0,
and ξ = x + by.
11. Seek a trial solution u (x, y)=f (x + my)sothatu
xx
= f
′′
, u
yy
=
m
2
f
′′
. Substituting into the Laplace equation yields
m
2
+1
f
′′
=0
which gives that either f
′′
=0orm
2
+1 = 0. Thus, m =+
i.The
general solution is u (x, y)=F (x + iy)+G (x − iy). Identifying c with
i gives the d’Alembert solution
u (x , y)=
1
2
[f (x + iy)+f (x − iy)] +
1
2i
x+iy
x−iy
g (α) dα.
12. (a) Hyperboli c. (ξ, η)=
2
3
y
3/2
+
x
3/2
,3
ξ
2
− η
2
u
ξη
= ηu
η
− ξu
η
.
(b) Elliptic.
dy
dx
=+
i sech
2
x, ξ = y + i tanh x, η = y − i tanh x;
α = y, β = tanh x.Thus,u
αα
+ u
ββ
=
2β
(1−β
2
)
u
β
.
(d) Hyperbolic. ξ = y + tanh x, η = y − tanh x.
u
ξη
=
"
4 − (ξ − η)
2
#
−1
(η − ξ)(u
ξ
− u
η
) in the domain (η − ξ)
2
< 4.
(e) Parabolic. ξ = y − 3x, η = y; u
ηη
= −
η
3
(u
ξ
+ u
η
).
(f) Elliptic. α =
1
2
y
2
− x
2
, β =
1
2
x
2
. The canonical form is
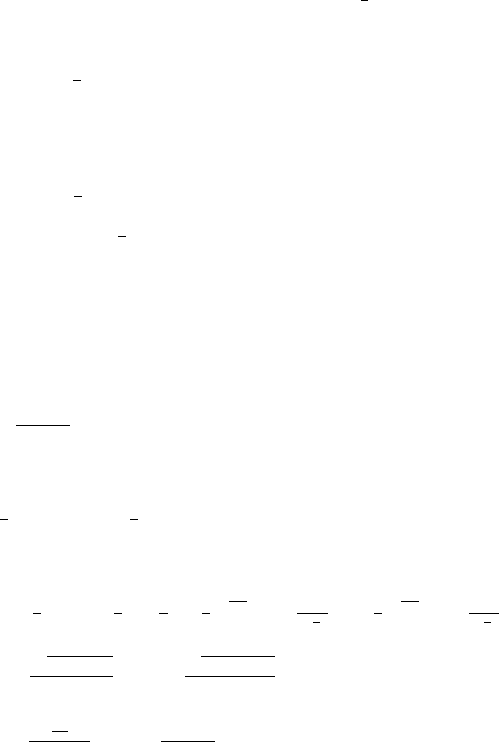
712 Answers and H ints to Selected Exercises
u
αα
+ u
ββ
=[2β (α + β)]
−1
[αu
α
− (α +2β) u
β
].
(g) Elliptic. α =sinx + y, β = x, u
αα
+ u
ββ
=(sinβ) u
α
− u.
(h) Parabolic. ξ = x +cosy, η = y.Thus,u
ηη
=
sin
2
η cos η
u
ξ
.
13. The general solution is
u (x , y)=e
x
x
0
e
−α
cos (α + ye
α−x
) dα + e
x
f (ye
−x
)+g (x),
where f and g are arbitrary functions.
5.12 Exercises
1. (a) u (x, t)=t,(b)u (x, t)=sinx cos ct + x
2
t +
1
3
c
2
t
3
,
(c) u (x, t)=x
3
+3c
2
xt
2
+ xt,(d)u (x, t)=cosx cos ct +(t/e),
(e) u (x, t)=2t +
1
2
log
1+x
2
+2cxt + c
2
t
2
+log
1+x
2
− 2cxt + c
2
t
2
!
,
(f) u (x, t)=x +(1/c)sinx sin ct.
2. (a) u (x, t)=3t +
1
2
xt
2
.
(c) u (x, t)=5+x
2
t +
1
3
c
2
t
3
+
1/2c
2
(e
x+ct
+ e
x−ct
− 2e
x
),
(e) u (x, t)=sinx cos ct +(e
t
− 1) (xt + x) − xte
t
,
(f) u (x, t)=x
2
+ t
2
1+c
2
+(1/c)cosx sin ct.
3. s (r, t)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
0, 0 ≤ t<r− R
s
0
(r−t)
2r
,r− R<t<r+ R
0,r+ R<t<∞
4. u (x, t)=
1
4
sin (y + x)+
3
4
sin (−y/3+x)+y
2
/3+xy.
5. u (x, t)=sinx cos at + xt,wherea is a physical constant.
6. (b) u (x, t)=
1
2
f (xt)+
1
2
tf
x
t
+
1
4
√
xt
x/t
xt
f(τ )
τ
3
2
dτ −
1
2
√
xt
x/t
xt
g (τ )
τ
3
2
dτ.
19. u (x, t)=f
√
y
2
+x
2
−8
2
+ g
√
y
2
−x
2
+16
2
− f (2).
22. u (x, t)=g
y −
x
2
2
+4
2
+ f
y +x
2
/2
2
− f (2).
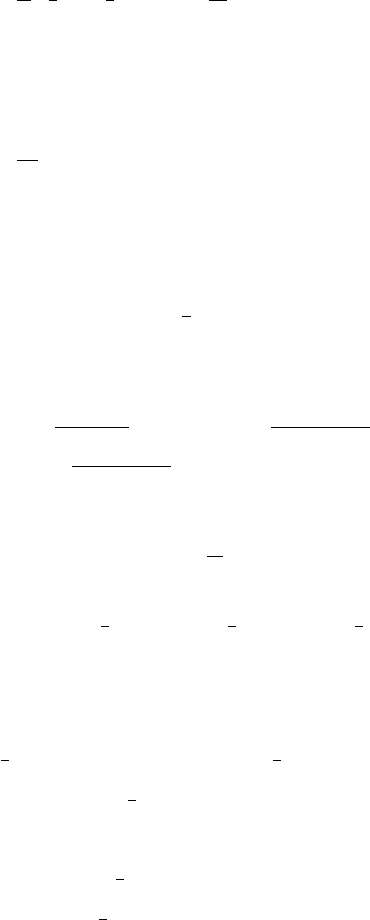
5.12 Exercises 713
28. The wave equation is
u
tt
− c
2
u
xx
= q (x, t) ,c
2
= T/ρ.
Multiply the wave equation by u
t
and rewrite to obtain
d
dt
1
2
u
2
t
+
1
2
c
2
u
2
x
− c
2
∂
∂x
(u
t
u
x
)=q (x, t) u
t
.
Integrating this result gives the energy equation. In view of the fact
that u
t
(0,t)=0=u
t
(l, t), the energy equation with no external forces
gives
dE
dt
=0⇒ E (t) = constant.
29. This problem is identically the same as that of (5.5.1). In this case
f (x)=0=g (x), and U (t)=p (t). So the solution is given by (5.5.2)
and (5.5.3). Consequently,
u (x , t)=
⎧
⎪
⎨
⎪
⎩
U
t −
x
c
,x<ct,
0,x>ct.
30. (a) When ω = ck,
u (x , t)=
1
(k
2
c
2
−ω
2
)
sin (kx − ωt) −
(ω −kc)
2kc(ω
2
−c
2
k
2
)
sin [k (x + ct)]
+
(ω +kc)
2kc(ω
2
−c
2
k
2
)
sin [k (x − ct)] .
This solution represents three harmonic waves which propagate with
different amplitudes and with speeds +
c and the phase velocity (ω/k).
(b) When ω = ck,
u (x , t)=
1
4
sin (x − t) −
1
4
sin (x + t)+
1
2
t cos (x − t) .
This solution represents two harmonic waves with constant amplitude
and another harmonic wave whose amplitude grows linearly with time.
31. (a) u (x, t)=
1
2
[cos ( x − 3t)+cos(x +3t)] +
1
6
x+3t
x−3t
sin (2α) dα
=cosx cos (3t)+
1
6
sin (2x)sin(6t).
(c) u (x, t)=cos(3x) cos (21t)+tx.
(e) u (x, t)=x
3
+27xt
2
+
1
6
[cos ( x +3t) − cos (x − 3t)]
+
1
6
[(x +3t)sin(x +3t) − (x − 3t)sin(x − 3t)].

714 Answers and H ints to Selected Exercises
(f) u (x, t)=
1
2
[cos ( x − 4t)+cos(x +4t)]
+
1
8
e
−x
(x +1− 4t) e
4t
− (x +1+4t) e
−4t
!
.
32. Verify that
u (x , t)=
t
0
v (x, t; τ ) dτ
satisfies the Cauchy problem.
u
t
(x, t)=v (x, t; t)+
t
0
v
t
(x, t; τ ) dτ =
t
0
v
t
(x, t; τ ) dτ
u
tt
(x, t)=v
t
(x, t; t)+
t
0
v
tt
(x, t; τ ) dτ = p (x, t)+
t
0
v
tt
(x, t; τ ) dτ
u
xx
(x, t)=
t
0
v
xx
(x, t; τ ) dτ.
Thus,
u
tt
− c
2
u
xx
= p (x, t)+
t
0
v
tt
− c
2
v
xx
dτ = p (x, t) .
33. u
t
= v (x, t; t)+
t
0
v
t
(x, t; τ ) dτ = p (x, t)+
t
0
v
t
(x, t; τ ) dτ
u
xx
=
t
0
v
xx
(x, t; τ ) dτ .
Hence,
u
t
− κu
xx
= p (x, t)+
t
0
(v
t
− κv
xx
) dτ = p (x, t).
34. According to the Duhamel p rin ciple
u (x , t)=
t
0
v (x, t; τ ) dτ
is the solution of the problem where v (x, t; τ) satisfies
v
t
= κv
xx
, 0 ≤ x<1,t>0,
v (0,t; τ )=0=v (1,t; τ),
v (x, τ ; τ )=e
−τ
sin πx, 0 ≤ x ≤ 1.
Using the separation of vari ables, the solution is given by
v (x, t)=X (x) T (t)sothat
X
′′
+ λ
2
X = 0 and T
′
+ κλ
2
T =0.
The solution is
v (x, t; τ )=
∞
n=1
a
n
(τ) e
−λ
2
n
κt
sin λ
n
x,
when λ
n
= nπ, n =1, 2, 3,....
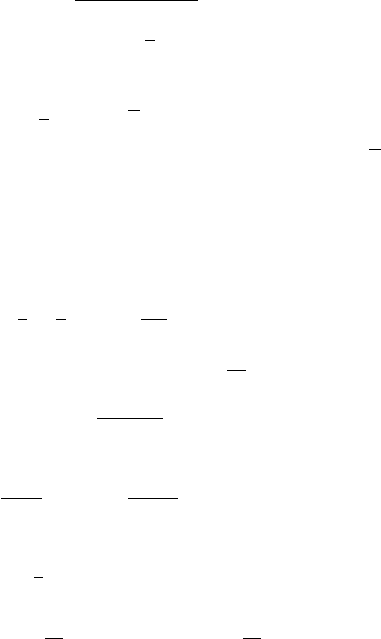
6.14 Exercises 715
Since v (x, τ; τ)=e
−τ
sin πx,
e
−τ
sin πx =
∞
n=1
a
n
(τ)exp
−n
2
π
2
κτ
sin (πnx).
Equating the coefficients gives
e
−τ
= a
1
(τ)exp
−π
2
κτ
,a
n
(τ)=0,n=2, 3,....
Consequently,
v (x, t; τ )=exp
π
2
κ − 1
τ
!
exp
−π
2
κt
sin πx.
Thus,
u (x , t)=exp
−π
2
κt
sin πx
t
0
exp
π
2
κ − 1
τ
!
dτ
=
e
−t
−exp
(
−π
2
κt
)
(π
2
κ−1)
· sin πx.
36. (a) The solution is u (x, t)=
1
n
e
nx
sin
2n
2
t + nx
+ e
−nx
sin
2n
2
t − nx
!
,
and u (x, t) →∞as n →∞for certain values of x and t.
(b) u
n
(x, y)=
1
n
exp (−
√
n )sinnx sinh ny is the solution. For y =0,
u
n
(x, y) →∞as n →∞.But(u
n
)
y
(x, 0) = exp (−
√
n )sinnx → 0as
n →∞.
6.14 Exercises
1. (a) f (x)=−
π
4
+
h
2
+
∞
k=1
(
1
πk
2
"
1+(−1)
k+1
#
cos kx
+
1
πk
"
h +(h + π)(−1)
k+1
#
sin kx
)
.
(c) f (x)=sinx +
∞
k=1
2(−1)
k+1
k
sin kx.
(e) f (x)=
sinh π
π
1+
∞
k=1
2(−1)
k
1+k
2
(cos kx − k sin kx)
.
2. (a) f (x)=
∞
k=1
2
k
sin kx
(b) f (x)=
∞
k=1
2
πk
"
1 − 2(−1)
k
+cos
kπ
2
#
sin kx.
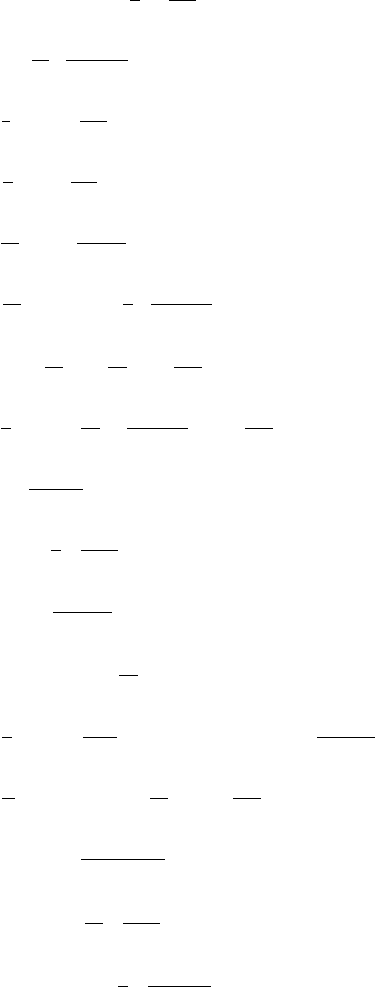
716 Answers and H ints to Selected Exercises
(c) f (x)=
∞
k=1
"
2(−1)
k+1
π
k
+
4
πk
3
(−1)
k
− 1
#
sin kx.
(d) f (x)=
∞
k=2
2k
π
"
1+(−1)
k
k
2
−1
#
sin kx.
3. (a) f (x)=
3
2
π +
∞
k=1
2
πk
2
"
(−1)
k
− 1
#
cos kx.
(b) f (x)=
π
2
+
∞
k=1
2
πk
2
"
(−1)
k
− 1
#
cos kx.
(c) f (x)=
π
2
3
+
∞
k=1
4(−1)
k
k
2
cos kx.
(d) f (x)=
2
3π
+
∞
k=1,2,4,...
6
π
"
1+(−1)
k
9−k
2
#
cos kx, k =3.
4. (b) f (x)=
∞
k=1
2
kπ
sin
kπ
2
cos
kπx
6
.
(c) f (x)=
2
π
+
∞
k=2
2
kπ
"
1+(−1)
k
1−k
2
#
cos
kπx
l
.
(f) f (x)=
∞
k=1
kπ
1+k
2
π
2
(−1)
k+1
e − e
−1
sin (kπx).
5. (a) f (x)=
∞
k=−∞
1
π
2+ik
4+k
2
(−1)
k
sinh 2πe
ikx
.
(b) f (x)=
∞
k=−∞
(−1)
k
π (1+k
2
)
sinh πe
ikx
.
(d) f (x)=
∞
k=−∞
(−1)
k
i
kπ
e
ikπx
.
6. (a) f (x)=
π
8
+
∞
k=1
"
1
2πk
2
(
(−1)
k
− 1
)
cos kx +
(−1)
k+1
2k
sin kx
#
.
7. (a) f (x)=
l
2
3
+
∞
k=1
4(−1)
k
1
kπ
2
cos
kπx
l
.
8. (a) sin
2
x =
∞
k=1,3,4,...
4(1−cos kπ )
kπ(4−k
2
)
sin kx.
(b) cos
2
x =
∞
k=1,3,4,...
2
kπ
1−k
2
4−k
2
(1 − cos kπ)sinkx.
(d) sin x cos x =
∞
k=1,3,4,...
2
π
1−cos kπ
4−k
2
cos kx.

6.14 Exercises 717
9. (a)
x
2
4
=
π
2
12
−
∞
k=1
(−1)
k+1
k
2
cos kx.
(c)
∞
0
ln
2cos
x
2
dx =
∞
k=1
(−1)
k+1
sin kx
k
2
.
(e)
π
2
−
4
π
∞
k=1
cos(2k−1)x
(2k−1)
2
=
⎧
⎪
⎨
⎪
⎩
−x, −π<x<0
x, 0 <x<π.
10. (a) f (x, y)=
16
π
2
∞
m=1,3,...
∞
n=1,3,...
1
mn
sin mx sin ny
(c) f (x, y)=
π
4
9
+
1
2
∞
m=1
8
3
π
2
(−1)
m
m
2
cos mx +
1
2
∞
n=1
8
3
π
2
(−1)
m
n
2
cos ny
+
∞
m=1
∞
n=1
16(−1)
m+n
m
2
n
2
cos mx cos ny.
(e) f (x, y)=
∞
m=1
2(−1)
m+1
m
sin mx sin y.
(g) f (x, y)=
∞
m=1
∞
n=1
d
mn
sin
mπ x
1
sin
nπy
2
,
where
d
mn
=
4
1.2
2
0
1
0
xy sin (mπx)sin
nπy
2
dx dy
=2
2
0
sin mπx
m
2
π
2
−
x cos mπx
mπ
1
0
y sin
nπy
2
dy
=
−2(−1)
m
mπ
2
0
y sin
nπy
2
dy =
−2(−1)
m
mπ
−4(−1)
n
nπ
=
8(−1)
m+n
π
2
mn
.
(h) f (x, y)=
16
π
2
∞
m=1
∞
n=1
[(2m − 1) (2n − 1)]
−1
sin
"
(2m−1)πx
a
#
×sin
"
(2n−1)πy
b
#
.
(Double Fourier sine series).
(i) f (x, y)=
sin 2
π
∞
m=1
(−1)
m+1
m
sin πmx

718 Answers and H ints to Selected Exercises
+
8sin2
π
∞
m=1
∞
n=1
"
(−1)
m+n+1
m(4−π
2
n
2
)
#
sin (mπx)cos
πny
2
.
(j) f (x, y)=
2
3
π
2
∞
m=1
(−1)
m+1
m
sin mx+
∞
m=1
∞
n=1
8(−1)
m+n+1
mn
2
sin mx cos ny.
(k) f (x, y)=
π
4
9
+
4π
2
3
∞
m=1
(−1)
m
m
2
cos mx +
∞
n=1
(−1)
n
n
2
cos ny
+16
∞
m=1
∞
n=1
(−1)
m+n
m
2
n
2
cos mx cos ny.
20. (a) b
2n
=0, b
2n+1
=
8
π (2n+1)
3
.
f (x)=x (π − x)=
8
π
sin x
1
3
+
sin 3x
3
3
+
sin 5x
5
3
+ ...
.
(b) Put x =
π
2
and x =
π
4
to find the sum of the series.
21. (a) b
n
=
2
π
π
0
f (x)sinnx dx =
8
n
2
π
2
sin
nπ
2
,n=0, 1, 2,....
b
2n
= 0 and b
2n+1
=
8(−1)
n
π
2
(2n+1)
2
,n=0, 1, 2,....
(b) Put x =
π
2
.
22. (a) f (x)=
∞
n=1
b
n
sin
nπx
a
,
b
n
=
2
a
a
0
sin
nπx
a
dx =
2
nπ
(1 − cos nπ)
=
2
nπ
[1 − (−1)
n
]=
⎧
⎪
⎨
⎪
⎩
4
nπ
, for od d n,
0, for even n.
f (x) ∼
4
π
sin
πx
a
+
1
3
sin
3πx
a
+
1
5
sin
5πx
a
+ ...
!
f (x) ∼
1
2
a
0
+
∞
n=1
a
n
cos
nπx
a
,a
0
=2,
a
n
=
2
nπ
(sin nπ − 0) = 0,n=0,
1=1+0· cos
nπ
a
+0· cos
2nπ
a
+ ...
(b) f (x)=
∞
n=1
(−1)
n+1
2a
nπ
sin
nπx
a
f (x) ∼
1
2
a
0
+
∞
n=1
a
n
cos
nπx
a
,wherea
0
=
2
a
a
0
xdx = a,
a
n
=
2
a
a
0
x cos
nπx
a
dx =
2a
n
2
π
2
((−1)
n
− 1)
= 0, for even n,and−
4a
n
2
π
2
, for odd n.

6.14 Exercises 719
23. (a) a
0
=
1
a
a
−a
xdx =0,
a
n
=
1
a
a
−a
x cos
nπx
a
dx =
x
nπ
sin
nπx
a
+
a
π
2
n
2
cos
nπx
a
!
a
−a
=
a
n
2
π
2
(cos nπ − cos (−nπ)) = 0
b
n
=
1
a
a
0
x sin
nπx
a
dx
=
−x
nπ
cos
nπx
a
+
a
n
2
π
2
sin
nπx
a
a
−a
=
−a
nπ
cos nπ +
−a
nπ
cos (−nπ)=(−1)
n+1
2a
nπ
.
(c) a
0
=
1
2π
2π
0
f (x) dx =
1
2π
2π
π
dx =
1
2
a
n
=
1
π
2π
0
f (x)cosnx dx =
1
π
2π
π
cos nx dx =0 foralln.
b
n
=
1
π
2π
0
f (x)sinnx dx =
1
π
2π
π
sin nx dx
=
1
π
[−1+(−1)
n
]=
⎧
⎪
⎨
⎪
⎩
0,nis even
−
2
nπ
,nis odd.
f (x)=
1
2
−
2
π
∞
k=0
sin(2k+1)x
(2k+1)
.
24. f (x)=
1
π
+
1
2
cos x
+
2
π
∞
n=1
(−1)
n+1
cos 2nx
(4n
2
−1)
.
26. Hint: An argument similar to that used in Section 6.5 can be employed
to prove this general Parseval relation. More precisely, use (6.5.10) for
(f +
g) to obtain
1
π
π
−π
(f +
g)
2
dx =
1
2
(a
0
+
α
0
)
2
+
∞
k=1
"
(a
k
+
α
k
)
2
+(b
k
+ β
k
)
2
#
.
Subtracting the later equality from the former gives
1
π
π
−π
f (x) g (x) dx =
a
0
α
0
2
+
∞
k=1
(a
k
α
k
+ b
k
β
k
) .
27. (a) f (x)=
2
π
∞
0
1
α
cos αx sin aα dα,(b)f (x)=
2
π
∞
0
sin πα sin αx
(1−α
2
)
dα.

720 Answers and H ints to Selected Exercises
33.
c
k
=
1
2π
π
−π
xe
−ikx
dx =
1
2π
xe
−ikx
−ik
π
−π
+
1
ik
π
−π
e
−ikx
dx
=
1
2π
πe
−ikπ
−ik
+
πe
ikπ
(−ik)
+
e
−ikπ
k
2
=
π
2π
e
ikπ
+ e
−ikπ
(−ik)
=
i cos kπ
k
=(−1)
k
i
k
.
c
0
=
1
2π
π
−π
xdx =0.
35. (a) f (x)=
∞
k=−∞
c
k
e
ikx
,
c
k
=
1
2
(a
k
− ib
k
)=
1
2π
π
−π
f (x) e
−ikx
dx,
=
1
4π
π
−π
"
e
i(a−k)x
+ e
−i(a+k)x
#
dx,
=
1
4πi (a − k)
"
e
i(a−k)x
#
π
−π
−
1
4πi (a + k)
"
e
−i(a+k)x
#
π
−π
=
1
2π
1
a − k
sin (a − k) π +
1
a + k
sin (a + k) π
.
This is a real quantity and hence, b
k
=0fork =1,2,3,...,and
a
k
=
2(−1)
k
a sin (πa)
π (a
2
− k
2
)
,k=0, 1, 2,....
Thus,
cos (ax)=
2a sin aπ
π
1
2a
2
−
cos x
k
2
− 1
2
+
cos 2x
k
2
− 2
2
− ...
.
Since cos ax is even, the above series is continuous, even at x =+
nπ.
(b) Putting π for x and treating a = x is a variable
cot πx =
2x
π
1
2x
2
+
1
x
2
− 1
2
+
1
x
2
− 2
2
+ ...
or,
cot πx −
1
πx
= −
2x
π
∞
n=1
1
(n
2
− x
2
)
.
(c) Since the convergence is uniform in any interval of the x-axis that
does not contain any integers, term-by-term integration in 0 <a<x<
1, gives
