Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


13.3 Linear Dispersive Waves 541
Figure 13.2.2 The solution u (x, t) for different times t =0,τ and 2τ ;the
characteristics are shown by the dotted lines; two of them from x = ξ
1
and
x = ξ
2
intersect at t>τ.
substituted in the equation, ∂/∂t, ∂/∂x, ∂/∂y,and∂/∂z produce factors
−iω, ik, il,andim respectively, and the solution exists provided ω and κ
κ
κ
are related by an equation
P (−iω, ik, il, im)=0. (13.3.3)
This equation is known as the dispersion relation. Evidently, we have a
direct correspondence between equation (13.3.1) and the dispersion relation
(13.3.3) through the correspondence
∂
∂t
↔−iω,
∂
∂x
,
∂
∂y
,
∂
∂z
↔ i (k, l,m) . (13.3.4)
Equation (13.3.1) and the corresponding dispersion relation (13.3.3) in-
dicate that the former can be derived from the latter and vice-versa by us-
ing (13.3.4). The dispersion relation characterizes the plane wave motion.
In many prob lems, the dispersion relation can be written in the explicit
form
ω = W (k, l,m) . (13.3.5)
The phase and the group velocities of the waves are defined by
C
p
(κ
κ
κ)=
ω
κ
6
κ
κ
κ, (13.3.6)
C
g
(κ
κ
κ)=∇
κ
κ
κ
ω, (13.3.7)

542 13 Nonlinear Partial Differential Equations with Applications
where
6
κ
κ
κ is the unit vector in the direction of wave vector κ
κ
κ.
In the one-dimensional case, (13.3.5)–(13.3.7) become
ω = W (k) ,C
p
=
ω
k
,C
g
=
dω
dk
. (13.3.8)
The one-dimensional waves given by (13.3.2) are called dispersive if the
group velocity C
g
≡ ω
′
(k) is not constant, that is, ω
′′
(k) = 0. Physically,
as time progresses, the different waves disperse in the medium with the
result that a single hump breaks into wavetrains.
Example 13.3.1.
(i) Linearized one-dimensional wave equation
u
tt
− c
2
u
xx
=0,ω=+
ck. (13.3.9)
(ii) Linearized Korteweg and de Vries (KdV) equation for long water waves
u
t
+ αu
x
+ βu
xxx
=0,ω= αk − βk
3
. (13.3.10)
(iii) Klein–Gordon equation
u
tt
− c
2
u
xx
+ α
2
u =0,ω=+
c
2
k
2
+ α
2
1
2
. (13.3.11)
(iv) Schr¨odinger equation in quantum mechanics and de Broglie waves
i ψ
t
−
V −
2
2m
∇
2
ψ =0, ω =
2
κ
2
2m
+ V, (13.3.12)
where V is a constant potential energy, and h =2π is the Planck
constant.
The grou p velocity of de Broglie wave is (κ
κ
κ/m), and through the corre-
spondence principle, ω is to be interpreted as the total energy,
2
κ
κ
κ
2
/2m
as the kinetic energy, and κ
κ
κ as the particle momentum. Hence, the group
velocity is the classical particle velocity.
(v) Equation for vibration of a beam
u
tt
+ α
2
u
xxxx
=0,ω=+
αk
2
. (13.3.13)
(vi) The dispersion relation for water waves in an ocean of depth h
ω
2
= gk tanh kh, (13.3.14)
where g is the acceleration due to gravity.
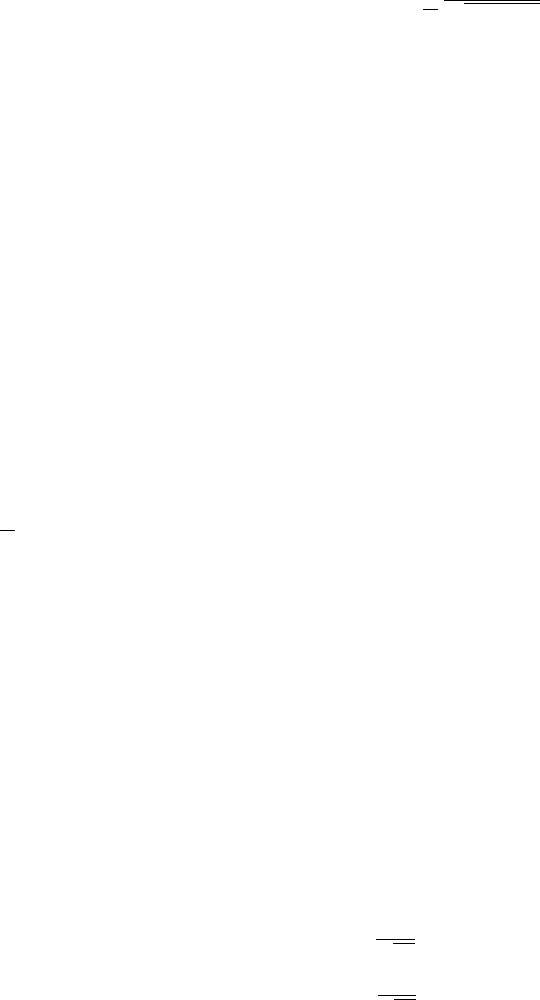
13.3 Linear Dispersive Waves 543
(vii) The Boussinesq equation
u
tt
− α
2
∇
2
u − β
2
∇
2
u
tt
=0,ω=+
ακ
1+β
2
κ
2
. (13.3.15)
This equ ation arises in elasticity for longitudinal waves in bars, long
water waves, and plasma waves.
(viii) Electromagnetic waves in dielectrics
u
tt
+ ω
2
0
u
u
tt
− c
2
0
u
xx
− ω
2
p
u
tt
=0,
ω
2
− ω
2
0
ω
2
− c
2
0
k
2
− ω
2
p
ω
2
=0, (13.3.16)
where ω
0
is the natural frequency of the oscillator, c
0
is the speed of
light, and ω
p
is the plasma frequency.
In view of the superpositi on principle, the general solution can be obtained
from (13.3.2) with the dispersion solution (13.3.3). For th e one-dimensional
case, the general solution has the Fourier integral representation
u (x , t)=
∞
−∞
F (k) e
i[kx−tW (k)]
dk, (13.3.17)
where F (k) is chosen to satisfy the initial or boundary data provided the
data are physically realistic enough to have Fourier transforms.
In many cases, as cited in Example 13.3.1, there are two modes ω =
+
W (k) so that the solution (13.3.17) has the form
u (x , t)=
∞
−∞
F
1
(k) e
i[kx−tW (k)]
dk +
∞
−∞
F
2
(k) e
i[kx−tW (k)]
dk, (13.3.18)
with the initial data at t =0
u (x , t)=φ (x) ,u
t
(x, t)=ψ (x) . (13.3.19)
The initial conditions give
φ (x)=
∞
−∞
[F
1
(k)+F
2
(k)] e
ikx
dk,
ψ (x)=−i
∞
−∞
[F
1
(k)+F
2
(k)] W (k) e
ikx
dk.
Applying the Fourier inverse transformations, we have
F
1
(k)+F
2
(k)=Φ (k)=
1
√
2π
∞
−∞
φ (x) e
−ikx
dx,
−iW (k)[F
1
(k) − F
2
(k)] = Ψ (k)=
1
√
2π
∞
−∞
ψ (x) e
−ikx
dx,

544 13 Nonlinear Partial Differential Equations with Applications
so that
[F
1
(k)+F
2
(k)] =
1
2
Φ (k)+
iΨ(k)
W (k)
. (13.3.20)
The asymptotic behavior of u (x, t) for large t with fixed (x/t)canbe
obtained by the Kelvin stationary phase approximation. For real φ (x),
ψ (x), Φ (−k)=Φ
∗
(k)andΨ (−k)=Ψ
∗
(k), where the asterisk denotes a
complex conjugate. It follows from (13.3.20) that, for W (k)even
[F
1
(−k) ,F
2
(−k)]=[F
∗
2
(k) ,F
∗
1
(k)] , (13.3.21)
and for W (k) odd,
[F
1
(−k) ,F
2
(−k)]=[F
∗
1
(k) ,F
∗
2
(k)] . (13.3.22)
In particular, when φ (x)=δ (x)andψ (x) ≡ 0, then F
1
(k)=F
2
(k)=
1/
√
8π, and the solution (13.3.18) reduces to the form
u (x , t)=
2
π
∞
0
cos kx cos {tW (k)}dk. (13.3.23)
In order to obtain the asymptotic approximation by the Kelvin station-
ary phase method (see Section 12.7) for t →∞, we consider both cases
when W (k)iseven(W
′
(k) is odd) and when W (k)isodd(W
′
(k)iseven)
and make an extra reasonable assumption that W
′
(k) is monotonic and
positive for k>0. It turns out that the asymptotic solution for t →∞is
u (x , t) ∼ 2Re
/
F
1
(k)
2π
t |W
′′
(k)|
1
2
exp
"
i
(
θ (x, t) −
π
4
sgn W
′′
(k)
)#
0
+ O
1
t
,
=Re
"
a (x, t) e
iθ(x,t)
#
, (13.3.24)
where k (x, t) is the positive root of the equation
W
′
(k)=
x
t
,ω= W (k) ,
x
t
> 0, (13.3.25ab)
θ (x, t)=xk(x, t) − tω(x, t) , (13.3.26)
and
a (x, t)=2F
1
(k)
2π
t |W
′′
(k)|
1
2
exp
−
iπ
4
sgn W
′′
(k)
. (13.3.27)
It is important to point out that solution (13.3.24) has a form similar
to that of the elementary plane wave solution, but k, ω,anda are no

13.4 Nonlinear Dispersive Waves and Whitham’s Equations 545
longer constants; they are functions of space variable x and time t.The
solution still represents an oscillatory wavetrain with the phase function
θ (x, t) describing the variations between local maxima and minima. Unlike
the elementary plane wavetrain, the present asymptotic result (13.3.24)
represents a nonuniform wavetrain in the sense that the amplitude, the
distance, and the time between successive maxima are not constant.
It also follows from (13.3.25a) that
k
t
k
= −
W
′
(k)
kW
′′
(k) t
1
t
∼ O
1
t
, (13.3.28)
k
x
k
= −
1
kW
′′
(k)
1
t
∼ O
1
t
. (13.3.29)
These results indicate the k (x, t) is a slowly varying function of x and t as
t →∞. Applying a similar argument to ω and a, we conclude that k (x, t),
ω (x, t), and a (x, t) are slowly varying functions of x and t as t →∞.
Finally, all these results seem to provide an imp ortant clue for natural
generalization of the concept of nonlinear and nonuniform wavetrains.
13.4 Nonlinear Dispersive Waves and Whitham’s
Equations
To describe a slowly varying nonlinear an d nonuniform oscillatory wavetrain
in a medium (see Whith am, 1974), we assume the existence of a solution
in the form (13.3.24) so that
u (x , t)=a (x, t) e
iθ(x,t)
+c.c., (13. 4.1)
where c.c. stands for the complex conjugate, a (x, t) is the complex ampli-
tude given by (13.3.27), an d the phase function θ (x, t)is
θ (x, t)=xk(x, t) − tω(x, t) , (13.4.2)
and k, ω,anda are slowly varying function of x and t.
Due to slow variations of k and ω, it is reasonable to assume that these
quantities still satisfy the dispersion relation
ω = W (k) . (13.4.3)
Differentiating (13.4.2) with respect to x and t respectively, we obtain
θ
x
= k + {x − tW
′
(k)}k
x
, (13.4.4)
θ
t
= −W (k)+{x − tW
′
(k)}k
t
. (13.4.5)
In the neighborhood of stationary points defined by (13.3.25a), these
results become

546 13 Nonlinear Partial Differential Equations with Applications
θ
x
= k (x, t) ,θ
t
= −ω (x, t) . (13.4.6)
These results can be used as a definition of local wavenumber and local
frequency of the slowly varying nonlinear wavetrain.
In view of (13.4.6), relation (13.4.3) gives a nonlinear partial differential
equation for the phase θ in the form
∂θ
∂t
+ W
∂θ
∂x
=0. (13.4.7)
The solution of this equation determines the geometry of the wave pattern.
However, it is convenient to eliminate θ from (13.4.6) to obtain
∂k
∂t
+
∂ω
∂t
=0. (13.4.8)
This is known as the Whitham equation for the conservation of waves, where
k represents the density of waves and ω is the flux of waves.
Using the dispersion relation (13.4.3), we obtain
∂k
∂t
+ C
g
(k)
∂k
∂x
=0, (13.4.9)
where C
g
(k)=W
′
(k) is the group velocity. This represents the simplest
nonlinear wave (hyperbolic) equation for the propagation of k with the
group velocity C
g
(k).
Since equation (13.4.9) is similar to (13.2.1), we can use the analysis of
Section 13.2 to find the general solution of (13.4.9) with the initial condition
k (x, 0) = f (x)att = 0. In this case, the solution has the form
k (x, t)=f (ξ) ,x= ξ + tF (ξ) , (13.4.10)
where F (ξ)=C
g
(f (ξ)). This further confirms the propagation of k with
the velocity C
g
. Some physical interpretations of this kind of solution have
already been discussed in Section 13.2.
Equations (13.4.9) and (13.4.3) reveal that ω also satisfies the nonlinear
wave (hyperbolic) equation
∂ω
∂t
+ W
′
(k)
∂ω
∂x
=0. (13.4.11)
It follows from equations (13.4.9) and (13.4.11) that both k and ω remain
constant on the characteristic curves defined by
dx
dt
= W
′
(k)=C
g
(k) , (13.4.12)
in the (x, t) plane. Since k and ω is constant on each curve, the characteristic
curves are straight lines with slope C
g
(k). The solution for k is given by
(13.4.10).
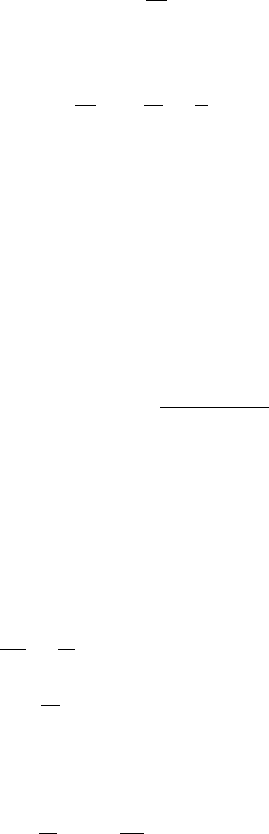
13.4 Nonlinear Dispersive Waves and Whitham’s Equations 547
Finally, it follows from the above analysis that any constant value of
the phase θ propagates according to θ (x, t) = constant, and hence,
θ
t
+
dx
dt
θ
x
=0, (13.4.13)
which gives, by (13.4.6),
dx
dt
= −
θ
t
θ
x
=
ω
k
= C
p
. (13.4.14)
Thus, the phase of the waves propagates with the phase speed C
p
.Onthe
other hand, (13.4.9) ensures that the wavenumber k propagates with the
group velocity C
g
(k)=(dω/dk)=W
′
(k).
We next investigate how the wave energy propagates in the dispersive
medium. We consider the following integral involving the square of the wave
amplitude (energy) given by (13.3.24) between any two points x = x
1
and
x = x
2
(0 <x
1
<x
2
)
Q (t)=
x
2
x
1
|a|
2
dx =
x
2
x
1
aa
∗
dx, (13.4.15)
=8π
x
2
x
1
F
1
(k) F
∗
1
(k)
t |W
′′
(k)|
dx, (13.4.16)
which is, due to a change of variable x = tW
′
(k),
=8π
k
2
k
1
F
1
(k) F
∗
1
(k) dk, (13.4.17)
where k
r
= tW
′
(k
r
), r =1, 2.
When k
r
is kept fixed as t varies, Q (t) remains constant so that
0=
dQ
dt
=
d
dt
x
2
x
1
|a|
2
dx,
=
x
2
x
1
∂
∂t
|a|
2
dx + |a|
2
2
W
′
(k
2
) −|a|
2
1
W
′
(k
1
) . (13.4.18)
In the limit x
2
− x
1
→ 0, this result reduces to the partial differential
equation
∂
∂t
|a|
2
+
∂
∂x
"
W
′
(k) |a|
2
#
=0. (13.4.19)
This represents the equation for the conservation of wave energy, where |a|
2
and |a|
2
W
′
(k) are the energy density and energy flux respectively. It al so
follows that the energy propagates with the group velocity W
′
(k). It has
been shown that the wavenumber k also propagates with the group velocity.
Evidently, the group velocity plays a double role.
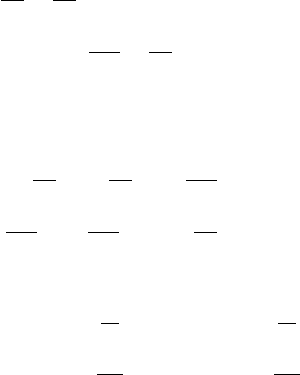
548 13 Nonlinear Partial Differential Equations with Applications
The above analysis reveals another imp ortant fact; equations (13.4.3),
(13.4.8), and (13.4.19) constitute a closed set of equations for the three
quantities k, ω,anda. Indeed, these are the fundamental equations for
nonlinear dispersive waves and are known as Whitham’s equations.
13.5 Nonlinear Instability
For infinitesimal waves, the wave amplitude (ak ≪ 1) is very small, so that
nonlinear effects can be neglected altogether. However, for finite ampli-
tude waves the terms i nvolving a
2
cannot be neglected, and the effects of
nonlinearity become important. In the theory of water waves, S tokes first
obtained the connection due to inherent nonlinearity between the wave-
profile and the frequency of a steady periodic wave system. According to
the Stokes theory, the remarkable fact is the dependence of ω on a which
couples (13.4.8) to (13.4.19). This leads to a new nonlinear phenomenon.
For finite amplitude waves, the frequency ω has the Stokes expansion
ω = ω
0
(k)+a
2
ω
2
(k)+...= ω
k, a
2
. (13.5.1)
This can be regarded as the nonlinear dispersion relation which depends on
both k and a
2
. In the linear case, the amplitude a → 0, (13.5.1) gives the
linear dispersion relation (13.4.3), that is, ω = ω
0
(k).
In order to discuss nonlinear instability, we substitute (13.5.1) into
(13.4.8) and retain (13.4.19) in the linear approximation to obtain the fol-
lowing coupled system:
∂k
∂t
+
∂
∂x
+
&
ω
0
(k)+ω
2
(k) a
2
'
=0, (13.5.2)
∂a
2
∂t
+
∂
∂x
&
ω
′
0
(k) a
2
'
=0, (13.5.3)
where W (k) ≡ ω
0
(k).
These equations can be further approximated to obtain
∂k
∂t
+ ω
′
0
∂k
∂x
+ ω
2
∂a
2
∂x
= O
a
2
, (13.5.4)
∂a
2
∂t
+ ω
′
0
∂a
2
∂x
+ ω
′′
0
a
2
∂k
∂x
=0. (13.5.5)
In matrix form, these equations read
⎛
⎝
ω
′
0
ω
2
ω
′′
0
a
2
ω
′
0
⎞
⎠
⎛
⎝
∂k
∂x
∂a
2
∂x
⎞
⎠
+
⎛
⎝
10
01
⎞
⎠
⎛
⎝
∂k
∂t
∂a
2
∂t
⎞
⎠
=0. (13.5.6)
Hence, the eigenvalues λ are th e roots of the determinant equation

13.6 The Traffic Flow Model 549
|a
ij
− λb
ij
| =
ω
′
0
− λω
2
ω
′′
0
a
2
ω
′
0
− λ
=0, (13.5.7)
where a
ij
and b
ij
are the coefficient matrices of (13.5.6). This equation gives
the characteristic velocities
λ =
dx
dt
= ω
′
0
+
(ω
2
ω
′′
0
)
1
2
a + O
a
2
. (13.5.8)
If ω
2
ω
′′
0
> 0, the characteristics are real and the system is hyperbolic.
The double characteristic velocity splits into two separate real velocities.
This provides a new extension of the group velocity to nonlinear problems. If
the disturbance is initially finite in extent, it would eventually split into two
disturbances. In general, any initial disturbance or modulating source would
introduce d istur bances in both families of characteristics. In the hyperbolic
case, compressive modulation will progressively distort and steepen so that
the question of breaking will arise. These results are remarkably different
from those found in linear theory, where there is only one characteristic
velocity and any hump may distort, due to the dependence of ω
′
0
(k)onk,
but would never split.
On the other hand, if ω
2
ω
′′
0
< 0, the characteristics are complex and the
system is elliptic. This leads to ill-p osed problems. Any small perturbations
in k and a will be given by the solutions of the form exp [iα (x − λt)] where λ
is calculated from (13.5.8) for unperturbed values of k and a. In this elliptic
case, λ is complex, and the perturbation will grow as t →∞. Hence, the
original wavetrain will become un stable. In the linear theory, the elliptic
case does not arise at all.
Example 13.5.1. For Stokes waves in deep water, the dispersion relation is
ω =(gk)
1
2
1+
1
2
k
2
a
2
, (13.5.9)
so that ω
0
(k)=(gk)
1
2
and ω
2
(k)=
1
2
√
gk
3
2
.
In thi s case, ω
′′
0
(k)=−
1
4
√
gk
−
3
2
so that ω
′′
0
ω
2
= −
g
8
k<0. The con-
clusion is that Stokes waves in deep water are definitely unstable. This is
one of the most remarkable results in the theory of nonlinear water waves
discovered during the 1960’s.
13.6 The Traffic Flow Model
We consider the flow of cars on a long highway under the assumptions that
cars do not enter or leave the highway at any one of its p oi nts. We take the
x-axis along the highway and assume that the traffic flows in th e positive

550 13 Nonlinear Partial Differential Equations with Applications
direction. Suppose ρ (x, t) is the density representing the numb er of cars
per unit l ength at the point x of the highway at time t,andq (x, t)isthe
flow of cars per unit time.
We assume a conservation law which states that the change in the total
amount of a physical quantity contained in any region of space must be
equal to the flux of that quantity across the boundary of that r egion. In
this case, the time rate of change of the total number of cars in any segment
x
1
≤ x ≤ x
2
of the highway is given by
d
dt
x
2
x
1
ρ (x, t) dx =
x
2
x
1
∂ρ
∂t
dx. (13.6.1)
This rate of change must be equal to the n et flux across x
1
and x
2
given by
q (x
1
,t) − q (x
2
,t) (13.6.2)
which measures the flow of cars entering the segment at x
1
minus the flow
of cars leaving the segment at x
2
. Thus, we have the conservation equation
d
dt
x
2
x
1
ρ (x, t) dx = q (x
1
,t) − q (x
2
,t) , (13.6.3)
or
x
2
x
1
∂ρ
∂t
dx = −
x
2
x
1
∂q
∂x
dx,
or
x
2
x
1
∂ρ
∂t
+
∂q
∂x
dx =0. (13.6.4)
Since the integrand in (13.6.4) is continuous, and (13.6.4) holds for every
segment [x
1
,x
2
], it follows that the integrand must vanish so that we have
the partial differential equation
∂ρ
∂t
+
∂q
∂x
=0. (13.6.5)
We now introduce an additional assumption which is supported by both
theoretical and experimental findings. According to this assumption, the
flow rate q depends on x and t only through the density, that is, q = Q (ρ)
for some function Q. This assumption seems to be reasonable in the sense
that the density of cars surrounding a given car indeed controls the speed of
that car. The functional relation between q and ρ depends on many factors,
including speed limits, weather conditions, and road characteristics. Several
specific relations are suggested by Haight (1963).
We consider here a particular relation q = ρv where v is the average
local velocity of cars. We assume that v is a function of ρ toafirstapproxi-
mation. In view of this relation, (13.6.5) reduces to the nonlinear hyperbolic
equation
