Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

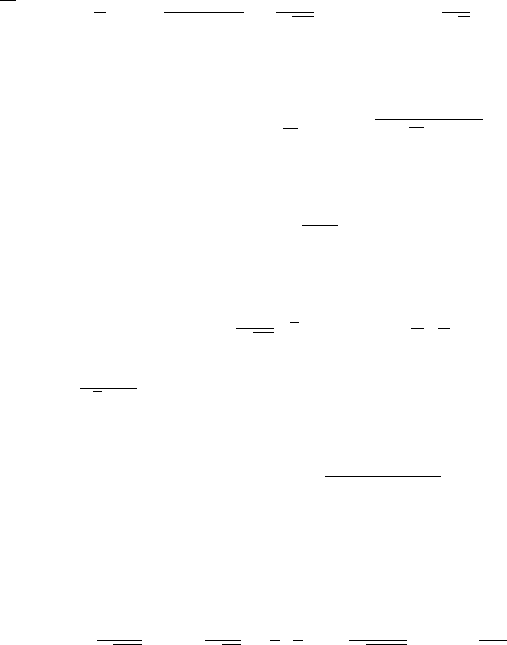
12.17 Solution of Fractional Partial Differential Equations 511
This i ntegral can be evaluated by using the Laplace transform of G (x, t)
as
G (x, s)=
1
π
∞
−∞
cos kx dk
s
α
+ κk
2
=
1
√
4κ
s
−α/2
exp
−
|x|
√
κ
s
α/2
, (12.17.11)
where
L
"
t
mα+β−1
E
(m)
α,β
(+
at
α
)
#
=
m! s
α−β
(s
α
+ a)
m+1
, (12.17.12)
and
E
(m)
α,β
(z)=
d
m
dz
m
E
α,β
(z) . (12.17.13)
The inverse Laplace transform of (12.17.11) gives the explicit solution
G (x, t)=
1
√
4κ
t
α
2
−1
W
−ξ,−
α
2
,
α
2
, (12.17.14)
where ξ =
|x|
√
κt
α/2
,andW (z,α, β) is the Wright function (see Erd´elyi 1953,
formula 18.1 (27)) defined by
W (z, α,β)=
∞
n=0
z
n
n! Γ (αn + β)
. (12.17.15)
It is important to note that when α = 1, the initial-value problem
(12.17.1)–(12.17.3) reduces to the classical diffusion problem and solution
(12.17.9) reduces to the classical solution because
G (x, t)=
1
√
4κt
W
−
x
√
κt
, −
1
2
,
1
2
=
1
√
4πκt
exp
−
x
2
4κt
. (12.17.16)
The fractional diffusion equation (12.17.1) has also been solved by other
authors including S chneider and Wyss (1989), Mainardi (1994, 1995), Deb-
nath (2003) and Nigmatulli n (1986) with a physical realistic initial condi-
tion
u (x , 0) = f (x) ,x∈ R. (12.17.17)
The solutions obtained by th ese authors are in total agreement with
(12.17.9).
It is noted that the order α of the derivative with respect to time t in
equation (12.17.1) can be of arbitrary real order including α = 2 so that
equation (12.17.1) may be called the fractional diffusion-wave equation.For
α = 2, it becomes the classical wave equation. The equation (12.17.1) with
1 <α≤ 2 will be solved next in some detail.

512 12 Integral Transform Methods with Applications
(b) Fractional Nonhomogeneous Wave Equation
The fractional nonhomogeneous wave equation is given by
∂
α
u
∂t
α
− c
2
∂
2
u
∂x
2
= q (x, t) ,x∈ R, t > 0 (12.17.18)
with the initial condition
u (x , 0) = f (x) ,u
t
(x, 0) = g (x) ,x∈ R, (12.17.19)
where c is a constant and 1 <α≤ 2.
Application of the joint Laplace transform with respect to t and the
Fourier transform with respect to x gives the transform solution
˜
¯u (k, s)=
˜
f (k) s
α−1
s
α
+ c
2
k
2
+
˜g (k) s
α−2
s
α
+ c
2
k
2
+
˜
¯q (k, s)
s
α
+ c
2
k
2
, (12.17.20)
where k is the Fourier transform variable and s is the Laplace transform
variable.
The inverse Laplace transform produces the following result:
˜u (k, t)=
˜
f (k) L
−1
s
α−1
s
α
+ c
2
k
2
+˜g (k) L
−1
s
α−2
s
α
+ c
2
k
2
+L
−1
˜
¯q (k, s)
s
α
+ c
2
k
2
, (12.17.21)
which, by (12.17.12),
=
˜
f (k) E
α,1
−c
2
k
2
t
α
+˜g (k) tE
α,2
−c
2
k
2
t
α
+
t
0
˜q (k, t − τ) τ
α−1
E
α,α
−c
2
k
2
τ
α
dτ. (12.17.22)
Finally, the inverse Fourier transform gives the formal solution
u (x , t)=
1
√
2π
∞
−∞
˜
f (k) E
α,1
−c
2
k
2
t
α
e
ikx
dk
+
1
√
2π
∞
−∞
t ˜g (k) E
α,2
−c
2
k
2
τ
α
e
ikx
dk
+
1
√
2π
t
0
τ
α−1
dτ
∞
−∞
˜q (k, t − τ) E
α,α
−c
2
k
2
τ
α
e
ikx
dk.
(12.17.23)
In particular, when α = 2, the fractional wave equation (12.17.18) re-
duces to the classical nonhomogeneous wave equation. In this particular
case, we use

12.17 Solution of Fractional Partial Differential Equations 513
E
2,1
−c
2
k
2
t
2
=cosh(ickt)=cos(ckt) , (12.17.24)
tE
2,2
−c
2
k
2
t
2
= t ·
sinh (ick t)
ickt
=
1
ck
sin ckt. (12.17.25)
Consequently, solution (12.17.23) reduces to solution (12.11.17) for α =
2as
u (x , t)=
1
√
2π
∞
−∞
˜
f (k) cos (ckt) e
ikx
dk +
1
√
2π
∞
−∞
˜g (k)
sin (ckt)
ck
e
ikx
dk
+
1
√
2πc
t
0
dτ
∞
−∞
˜q (k, τ)
sin ck (t − τ )
k
e
ikx
dk (12.17.26)
=
1
2
[f (x − ct)+f (x + ct)] +
1
2c
x+ct
x−ct
g (ξ) dξ
+
1
2c
t
0
dτ
x+c(t−τ)
x−c(t−τ)
q (ξ,τ ) dξ. (12.17.27)
We now derive the solution of the nonhomogeneous fractional diffusion
equation (12.17.18) with c
2
= κ and g (x) = 0. In this case, the joint
transform solution (12.17.20) becomes
˜
¯u (k, s)=
˜
f (k) s
α−1
(s
α
+ κk
2
)
+
˜
¯q (k, s)
(s
α
+ κk
2
)
(12.17.28)
which is inverted by using (12.17.12) to obtain ˜u (k, t) in the form
˜u (k, t)
=
˜
f (k) E
α,1
−κk
2
t
α
+
t
0
(t − τ)
α−1
E
α,α
&
−κk
2
(t − τ)
α
'
˜q (k, τ) dτ.
(12.17.29)
Finally, the inverse Fourier transform gives the exact solution
u (x , t)=
1
√
2π
∞
−∞
˜
f (k) E
α,1
−κk
2
t
α
e
ikx
dk
+
1
√
2π
t
0
dτ
∞
−∞
(t − τ)
α−1
E
α,α
&
−κk
2
(t − τ)
α
'
˜q (k, τ) e
ikx
dk.
(12.17.30)
Application of the Convolution Theorem of the Fourier transform gives
the final solution in the form
u (x , t)=
∞
−∞
G
1
(x − ξ, t) f (ξ) dξ
+
t
0
(t − τ)
α−1
dτ
∞
−∞
G
2
(x − ξ, t − τ ) q (ξ, τ) dξ, (12.17.31)
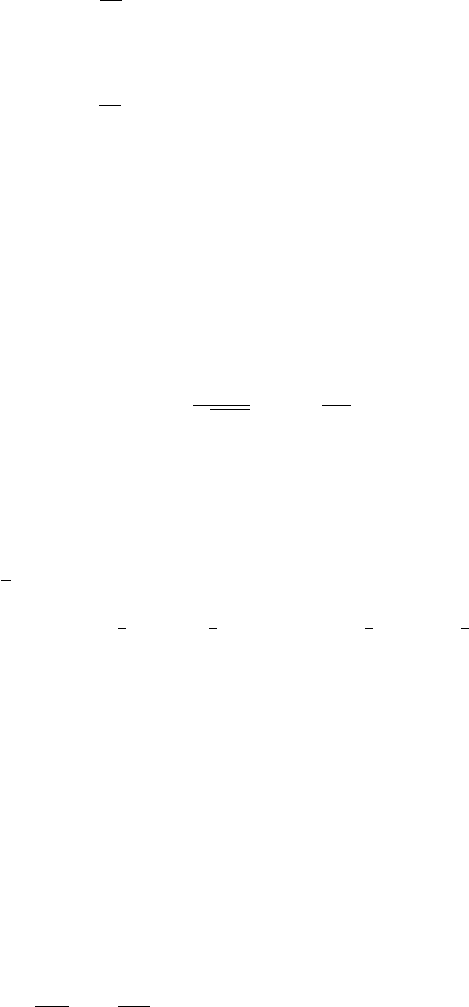
514 12 Integral Transform Methods with Applications
where
G
1
(x, t)=
1
2π
∞
−∞
e
ikx
E
α,1
−κk
2
t
α
dk, (12.17.32)
and
G
2
(x, t)=
1
2π
∞
−∞
e
ikx
E
α,α
−κk
2
t
α
dk. (12.17.33)
In particular, when α = 1, the classical solution of the nonhomogeneous
diffusion equation (12.17.18) is obtained in the form
u (x , t)=
∞
−∞
G
1
(x − ξ, t) f (ξ) dξ
+
t
0
dτ
∞
−∞
G
2
(x − ξ, t − τ ) q (ξ, τ) dξ, (12.17.34)
where
G
1
(x, t)=G
2
(x, t)=
1
√
4πκt
exp
−
x
2
4κt
. (12.17.35)
In the case of classical homogeneous diffusion equation (12.17.18), so-
lutions (12.17.30) and (12.17.34) are in perfect agreement with those of
Mainardi (1996), who obtained the solution by using the Laplace trans-
form method together with complicated evaluation of the Laplace inversion
integral and the auxiliary function M (z,α). He obtained the solution in
terms of M
z,
α
2
and discussed the nature of the solution for different
values of α. He made some comparisons between ordinary diffusion (α =1)
and fractional diffusion
α =
1
2
and α =
2
3
. For cases α =
4
3
and α =
3
2
,the
solution exhibits a striking difference from ordinary di ffusion with a tran-
sition from the Gaussian function centered at z = 0 (ordinary diffusion) to
the Dir ac delta function centered at z = 1 (wave propagation). This indi-
cates a possibility of an intermediate process between diffusion and wave
propagation. A special difference is observed between the solution s of the
fractional diffusion equation (0 <α≤ 1) and the fractional wave equation
(1 <α≤ 2). In ad diti on, the solution exhibits a slow process for the case
with 0 <α≤ 1 and an intermediate process for 1 <α≤ 2.
(c) Fractional-Order Diffusion Equation in Semi-Infinite Medium
We consider the fractional-order diffusion equation in a semi-infinite
medium x>0, when the boundary is kept at a temperature u
0
f (t) and the
initial temperature is zero in the whole medium. Thus, the initial boundary-
value problem is governed by the equation
∂
α
u
∂t
α
= κ
∂
2
u
∂x
2
, 0 <x<∞,t>0, (12.17.36)
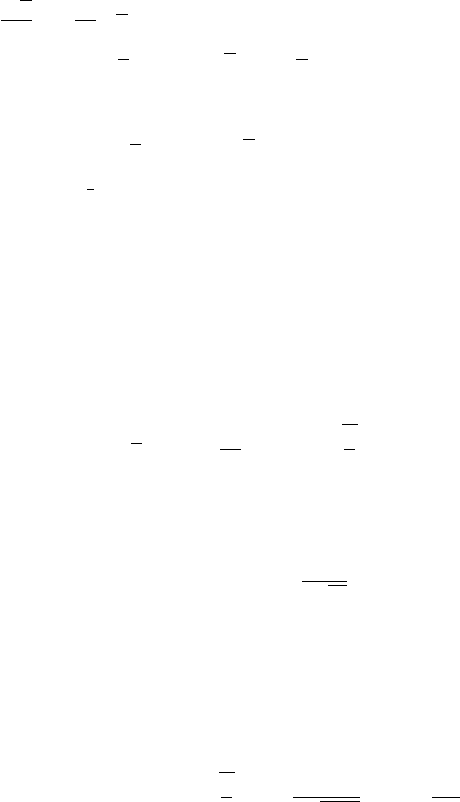
12.17 Solution of Fractional Partial Differential Equations 515
with
u (x , 0) = 0,x>0, (12.17.37)
u (0,t)=u
0
f (t) ,t>0, and u (x, t) → 0asx →∞. (12.17.38)
Application of the Laplace transform with respect to t gives
d
2
u
dx
2
−
s
α
κ
u (x , s)=0,x>0, (12.17.39)
u (0,s)=u
0
f (s) , u (x, s) → 0asx →∞.(12.17.40)
Evidently, the solution of this transformed boundary-value problem is
u (x , s)=u
0
f (s)exp(−ax) , (12.17.41)
where a =(s
α
/κ)
1
2
. Thus, the solu tion (12.17.41) is given by
u (x , t)=u
0
t
0
f (t − τ ) g (x, τ) dτ = u
0
f (t) ∗ g (x, t) , (12.17.42)
where
g (x, t)=L
−1
{exp (−ax)}.
When α = 1 and f (t) = 1, solution (12.17.41) becomes
u (x , s)=
u
0
s
exp
−x
s
κ
, (12.17.43)
which yields the classical solution in terms of the complementary error
function (see Debnath 1995)
u (x , t)=u
0
erfc
x
2
√
κt
. (12.17.44)
In the classical case (α = 1), the more general solution is given by
u (x , t)=u
0
t
0
f (t − τ ) g (x, τ) dτ = u
0
f (t) ∗ g (x, t) , (12.17.45)
where
g (x, t)=L
−1
exp
−x
s
κ
=
x
2
√
πκt
3
exp
−
x
2
4κt
. (12.17.46)
(d) The Fractional Stokes and Rayleigh Problems in Fluid Dynamics
The classical Stokes problem (see Debnath 1995) deals with the un-
steady boundary layer flows induced in a semi-infinite viscous fluid bounded
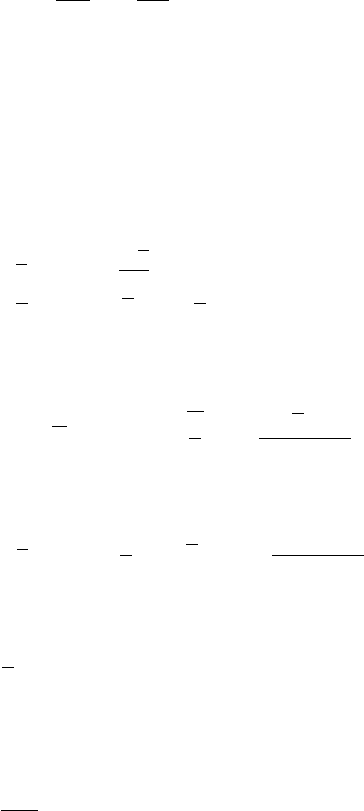
516 12 Integral Transform Methods with Applications
by an infinite horizontal disk at z = 0 due to nontorsional oscillations of
the disk in its own plane with a given frequency ω.Whenω =0,the
Stokes problem reduces to the classical Rayleigh problem where the un-
steady boundary layer flow is generated in the fluid from rest by moving
the disk impulsively in its own plane with constant velocity U.
We consider the u nsteady fractional boundary layer equation for the
fluid velocity u (z, t) that satisfies the equation
∂
α
u
∂t
α
= ν
∂
2
u
∂z
2
, 0 <z<∞,t>0, (12.17.47)
with the given boundary and initial condi tions
u (0,t)=Uf (t) ,u(z, t) → 0asz →∞,t>0, (12.17.48)
u (z, 0) = 0 for all z>0, (12.17.49)
where ν is the kinematic viscosity, U is a constant velocity, and f (t)isan
arbitrary function of time t.
Application of the Laplace transform with respect to t gives
s
α
u (z, s)=ν
d
2
u
dz
2
, 0 <z<∞, (12.17.50)
u (0,s)=U f (s) , u (z, s) → 0asz →∞. (12.17.51)
Use of the Fourier sine transform (see Debnath 1995) with respect to z
yields
U
s
(k, s)=
2
π
νU
k
f (s)
(s
α
+ νk
2
)
. (12.17.52)
The inverse Fourier sine transform of (12.17.52) leads to the solution
u (z, s)=
2
π
νU
f (s)
∞
0
k sin kz
(s
α
+ νk
2
)
dk, (12.17.53)
and the inverse Laplace transform gives the solution for the velocity
u (z, t)=
2
π
νU
∞
0
k sin kz dk
t
0
f (t − τ ) τ
α−1
E
α,α
−νk
2
τ
α
dτ.
(12.17.54)
When f (t)=exp(iωt), th e solution of the fractional Stokes problem is
u (z, t)=
2νU
π
e
iω t
∞
0
k sin kz dk
t
0
e
−iω τ
τ
α−1
E
α,α
−νk
2
τ
α
dτ.
(12.17.55)

12.17 Solution of Fractional Partial Differential Equations 517
When α = 1, solution (12.17.55) reduces to the classical Stokes solution
u (z, t)=
2νU
π
∞
0
1 − e
−νtk
2
k sin kz
(iω + νk
2
)
dk. (12.17.56)
For the fractional Rayleigh problem, f (t) = 1 and the solution follows
from (12.17.54) in the form
u (z, t)=
2νU
π
∞
0
k sin kz dk
t
0
τ
α−1
E
α,α
−νk
2
τ
α
dτ. (12.17.57)
This solution reduces to the classical Rayleigh solution when α =1as
u (z, t)=
2νU
π
∞
0
k sin kz dk
t
0
E
1,1
−ντ k
2
dτ
=
2νU
π
∞
0
k sin kz dk
t
0
exp
−ντ k
2
dτ
=
2U
π
∞
0
1 − e
−νtk
2
sin kz
k
dk,
which is (by (2.10.10) of Debnath 1995),
=
2U
π
π
2
−
π
2
erf
z
2
√
νt
= Uerfc
z
2
√
νt
. (12.17.58)
The above analysis is in full agreement with the classical solutions of
the Stokes and Rayleigh problems (see Debnath 1995).
(e) The Fractional Unsteady Couette Flow
We consider the unsteady viscous fluid flow between the plate at z =0at
rest and th e plate z = h in motion parallel to itself with a vari able velocity
U (t)inthex-direction. The fluid velocity u (z, t) satisfies the fractional
equation of motion
∂
α
u
∂t
α
= P (t)+ν
∂
2
u
∂z
2
, 0 ≤ z ≤ h, t > 0, (12.17.59)
with the boundary and initial conditions
u (0,t)=0andu (h, t)=U (t) ,t>0, (12.17.60)
u (z, t)=0 at t ≤ 0 for 0 ≤ z ≤ h, (12.17.61)
where −
1
ρ
p
x
= P (t)andν is the kinematic viscosity of th e fluid.
We apply the joint Laplace transform with respect to t and the finite
Fourier sine transform with resp ect to z defined by
¯
˜u
s
(n, s)=
∞
0
e
−st
dt
h
0
u (z, t)sin
nπz
h
dz (12.17.62)

518 12 Integral Transform Methods with Applications
to the system (12.17.59)–(12.17.61) so that the transform solution is
¯
˜u
s
(n, s)=
P (s)
1
a
[1 − (−1)
n
]
(s
α
+ νa
2
)
+
νa(−1)
n+1
U (s)
(s
α
+ νa
2
)
, (12.17.63)
where a =
nπ
h
and n is the finite Fourier sine transform variable.
Thus, the inverse Laplace transform yields
˜u
s
(n, t)=
1
a
[1 − (−1)
n
]
t
0
P (t − τ ) τ
α−1
E
α,α
−νa
2
τ
α
dτ
+νa(−1)
n+1
t
0
U (t − τ ) τ
α−1
E
α,α
−νa
2
τ
α
dτ. (12.17.64)
Finally, the inverse finite Fourier sine transform leads to the solution
u (z, t)=
2
h
∞
n=1
˜u
s
(n, t)sin
nπz
h
. (12.17.65)
In particular, when α =1,P (t) = constant, and U (t) = constant, then
solution (12.17.65) reduces to the solution of the generalized Couette flow
(see p. 277 Debnath 1995).
(f) Fractional Axisymmetric Wave-Diffusion Equation
The fractional axisymmetric wave-diffusion equation in an infinite do-
main
∂
α
u
∂t
α
= a
∂
2
u
∂r
2
+
1
r
∂u
∂r
, 0 <r<∞,t>0, (12.17.66)
is called the diffusion or wave equation accordingly as a = κ or a = c
2
.
For the fractional diffusion equation, we prescribe the initial condition
u (r, 0) = f (r) , 0 <r<∞. (12.17.67)
Application of the joint Laplace transform with respect to t and the Hankel
transform of zero order (see Section 12.12) with respect to r to (12.17.66)
and (12.17.67) gives th e transform solution
¯
˜u (k, s)=
s
α−1
˜
f (k)
(s
α
+ κk
2
)
, (12.17.68)
where k, s are the Hankel and Laplace transform var iabl es respectively.
The joint inverse transform leads to the solution
u (r, t)=
∞
0
kJ
0
(kr)
˜
f (k) E
α,1
−κk
2
t
α
dk, (12.17.69)

12.17 Solution of Fractional Partial Differential Equations 519
where J
0
(kr) is the Bessel f un ction of the first kind of order zero and
˜
f (k)
is the zero-order Hankel tran sform of f (r).
When α = 1, solution (12.17.69) reduces to the classical solution that
was obtained by Debnath (see p 66, Debnath 2005).
On the other hand, we can solve the wave equation (12.17.66) with
a = c
2
and the initial conditions
u (r, 0) = f (r) ,u
t
(r, 0) = g (r) for 0 <r<∞, (12.17.70)
provided the Hankel transforms of f (r)andg (r) exist.
Application of the joint Laplace and Hankel transform leads to the trans-
form solution
¯
˜u (k, s)=
s
α−1
˜
f (k)
(s
α
+ c
2
k
2
)
+
s
α−2
˜g (k)
(s
α
+ c
2
k
2
)
. (12.17.71)
The joint inverse transformation gives the solution
u (r, t)=
∞
0
kJ
0
(k, r)
˜
f (k) E
α,1
−c
2
k
2
t
α
dk
+
∞
0
kJ
0
(k, r)˜g (k) tE
α,2
−c
2
k
2
t
α
dk. (12.17.72)
When α = 2, (12.17.72) reduces to the classical solution (12.13.6).
In a finite domain 0 ≤ r ≤ a, the fractional diffusion equation (12.17.66)
has the boundary and initial data
u (r, t)=f (t)onr = a, t > 0, (12.17.73)
u (r, 0) = 0 for all r in (0,a) . (12.17.74)
Application of the joint Laplace and finite Hankel transform of zero order
(see pp. 317, 318, Debnath 1995) yields the solution
u (r, t)=
2
a
2
∞
i=1
˜u (k
i
,t)
J
0
(rk
i
)
J
2
1
(ak
i
)
, (12.17.75)
where
˜u (k
i
,t)=(aκ k
i
) J
1
(ak
i
)
t
0
f (t − τ ) τ
α−1
E
α,α
−κk
2
i
τ
α
dτ. (12.17.76)
When α = 1, (12.17.75) reduces to (12.16.7).
Similarly, the fractional wave equation (12.17.66) with a = c
2
in a finite
domain 0 ≤ r ≤ a with the boundary and initial conditions
u (r, t)=0onr = a, t > 0, (12.17.77)
u (r, 0) = f (r)andu
t
(r, 0) = g (r) for 0 <r<a, (12.17.78)
520 12 Integral Transform Methods with Applications
can be solved by means of the joint Laplace and finite Hankel transforms.
The solution of this problem is
u (r, t)=
2
a
2
∞
i=1
˜u (k
i
,t)
J
0
(rk
i
)
J
2
1
(ak
i
)
, (12.17.79)
where
˜u (k
i
,t)=
˜
f (k
i
) E
α,1
−c
2
k
2
i
t
α
+˜g (k
i
) tE
α,2
−c
2
k
2
i
t
α
. (12.17.80)
When α = 2, solution (12.17.79) reduces to the solution (11.4.26) obtained
by Debnath (1995).
(g) The Fractional Schr¨odinger Equation in Quantum Mechan ics
The one-dimensional fractional Schr¨odinger equation for a free particle
of mass m is
i
∂
α
ψ
∂t
α
= −
2
2m
∂
2
ψ
∂x
2
, −∞ <x<∞,t>0, (12.17.81)
ψ (x, 0) = ψ
0
(x) , −∞ <x<∞, (12.17.82)
ψ (x, t) → 0as |x|→∞, (12.17.83)
where ψ (x, t) is the wave function, h =2π =6.625 × 10
−27
erg sec =
4.14 × 10
−21
MeV sec is the Planck constant, and ψ
0
(x) is an arbitrary
function.
Application of the joint Laplace and Fourier transform to (12.17.81)–
(12.17.83) gives the solution in the transform space in the form
Ψ (k, s)=
s
α−1
Ψ
0
(k)
s
α
+ ak
2
,a=
i
2m
, (12.17.84)
where k, s represent the Fourier and the Laplace transforms variables.
The use of the joint inverse transform yields the solution
ψ (x, t)=
1
√
2π
∞
−∞
e
ikx
˜
ψ
0
(k) E
α,1
−ak
2
t
α
dk. (12.17.85)
= F
−1
(
˜
ψ
0
(k) E
α,1
−ak
2
t
α
)
, (12.17.86)
which is, by Theorem 12.4.1, the Convolu tion Theorem of the Fourier trans-
form
=
∞
−∞
G (x − ξ, t) ψ
0
(ξ) dξ, (12.17.87)
where
G (x, t)=
1
√
2π
F
−1
&
E
α,1
−ak
2
t
α
'
=
1
2π
∞
−∞
e
ikx
E
α,1
−ak
2
t
α
dk. (12.17.88)
