Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

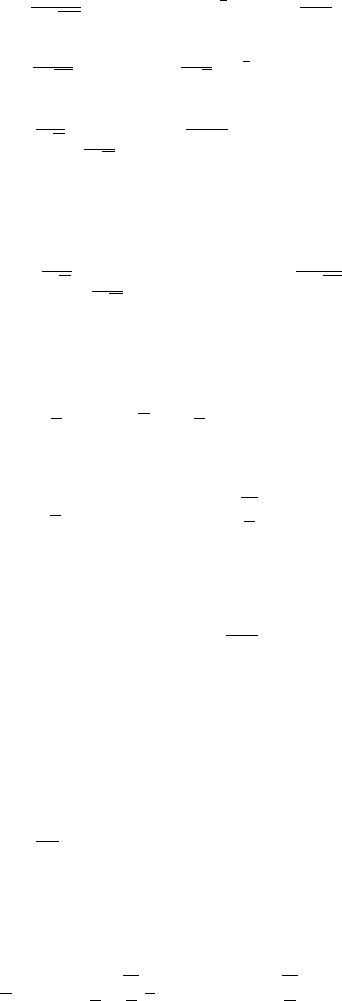
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 481
The Laplace inversion theorem gives the solution
u (x , t)=
x
2
√
πκ
t
0
f (t − τ ) τ
−
3
2
exp
−
x
2
4κτ
dτ, (12.11.24)
which, by setting λ =
x
2
√
κτ
,or dλ = −
x
4
√
κ
τ
−
3
2
dτ,
=
2
√
π
∞
x
2
√
κt
f
t −
x
2
4κλ
2
e
−λ
2
dλ. (12.11.25)
This is the formal solution of the heat conduction problem.
In particular, if f (t)=T
0
= constant, soluti on (12.11.25) becomes
u (x , t)=
2T
0
√
π
∞
x
2
√
κt
e
−λ
2
dλ = T
0
erfc
x
2
√
κt
. (12.11.26)
Clearly, the temperature distribution tends asymptotically to the constant
value T
0
,ast →∞.
Alternatively, solution (12.11.23) can be written as
u (x , s)=f (s) s u
0
(x, s) , (12.11.27)
where
s
u
0
(x, s)=exp
−x
s
κ
. (12.11.28)
Consequently, the i nversion of (12.11.27) gives a new representation
u (x , t)=
t
0
f (t − τ )
∂u
0
∂τ
dτ. (12.11.29)
This is called the Duhamel formula for the diffusion equation .
We consider another physical problem: determining the temperature
distribution of a semi-infinite solid when the rate of flow of heat is prescribed
at the end x = 0. Thus, the problem is to solve diffusion equation (12.11.18)
subject to conditions (12.11.19), ( 12.11.21), and
−k
∂u
∂x
= g (t)atx =0,t>0, (12.11.30)
where k is a constant called thermal conductivity.
Application of the Laplace transform gives the solution of the trans-
formed problem
u (x , s)=
1
k
κ
s
g (s)exp
−x
s
κ
. (12.11.31)

482 12 Integral Transform Methods with Applications
The inverse Laplace transform yields the solution
u (x , t)=
1
k
κ
π
t
0
g (t − τ) τ
−
1
2
exp
−
x
2
4κτ
dτ, (12.11.32)
which is, by the change of variable λ =
x
2
√
κτ
,
=
x
k
√
π
∞
x
2
√
κt
g
t −
x
2
4κλ
2
λ
−2
e
−λ
2
dλ. (12.11.33)
In particular, if g (t)=T
0
= constant, th is solution becomes
u (x , t)=
T
0
x
k
√
π
∞
x
√
4κt
λ
−2
e
−λ
2
dλ.
Integrating this result by parts gives
u (x , t)=
T
0
k
2
κt
π
exp
−
x
2
4κt
− x erfc
x
2
√
κt
. (12.11.34)
Alternatively, the heat conduction problem (12.11.18)–(12.11.21) can be
solved by using fractional derivatives (Debnath 1995). We recall (12.11.23)
and rewrite it as
∂
u
∂x
= −
s
κ
u. (12.11.35)
This can be expressed in terms of a fractional derivative of order
1
2
as
∂u
∂x
= −
1
√
κ
L
−1
&
√
s u (x, s)
'
= −
1
√
κ
0
D
1
2
t
u (x , t) . (12.11.36)
Thus, the heat flux is expressed in terms of the fractional derivative. In
particular, when u (0,t)=constant=T
0
, then the heat flux at the surface
is given by
−k
∂u
∂x
x=0
=
k
√
κ
D
1
2
t
T
0
=
kT
0
√
πκt
. (12.11.37)
Example 12.11.8. (Diffusion Equation in a Finite Medium). Solve the dif-
fusion equation
u
t
= κu
xx
, 0 <x<a, t>0, (12.11.38)
with the initial and boundary conditions
u (x , 0) = 0, 0 <x<a, (12.11.39)
u (0,t)=U, t > 0, (12.11.40)
u
x
(a, t)=0,t>0, (12.11.41)
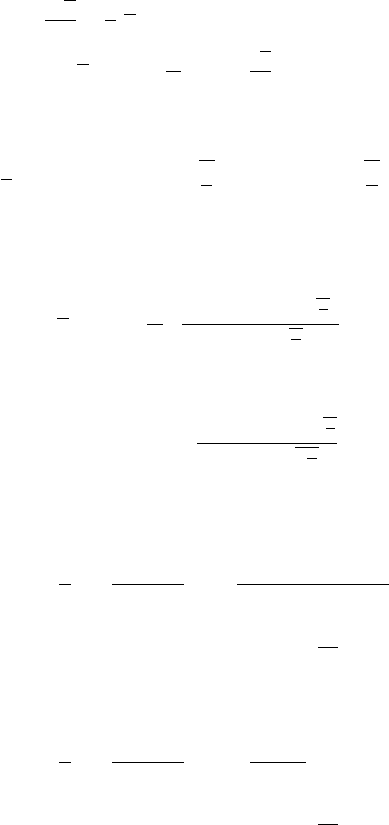
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 483
where U is a constant.
We introduce the Laplace transform of u (x, t) with respect to t to obtain
d
2
u
dx
2
−
s
κ
u =0, 0 <x<a, (12.11.42)
u (0,s)=
U
s
,
d
u
dx
x=a
=0. (12.11.43)
The general solution of (12.11.42) is
u (x , s)=A cosh
x
s
κ
+ B sinh
x
s
κ
, (12.11.44)
where A and B are constants of integration. Using (12.11.43), we obtain
the values of A and B, so that the solution (12.11.44) becomes
u (x , s)=
U
s
·
cosh
(a − x)
s
κ
!
cosh
a
s
κ
. (12.11.45)
The inverse Laplace transform gives the solution
u (x , t)=UL
−1
/
cosh (a − x)
s
κ
s cosh
a
s
κ
0
. (12.11.46)
The inversion can be carried out by the Cauchy residue theorem to obtain
the solution
u (x , t)=U
1+
4
π
∞
n=1
(−1)
n
(2n − 1)
cos
(2n − 1) (a − x) π
2a
× exp
−(2n − 1)
2
π
2a
2
κt
. (12.11.47)
By expanding the cosine term, this becomes
u (x , t)=U
1 −
4
π
∞
n=1
1
(2n − 1)
sin
2n − 1
2a
πx
× exp
−(2n − 1)
2
π
2a
2
κt
. (12.11.48)
This result can be obtained by solving the problem by the method of sep-
aration of variables.
Example 12.11.9. (Diffusion in a Finite Medium). Solve the one-dimensional
diffusion equation in a finite medium 0 <z<a, where the concentration
function C (z, t) satisfies the equation
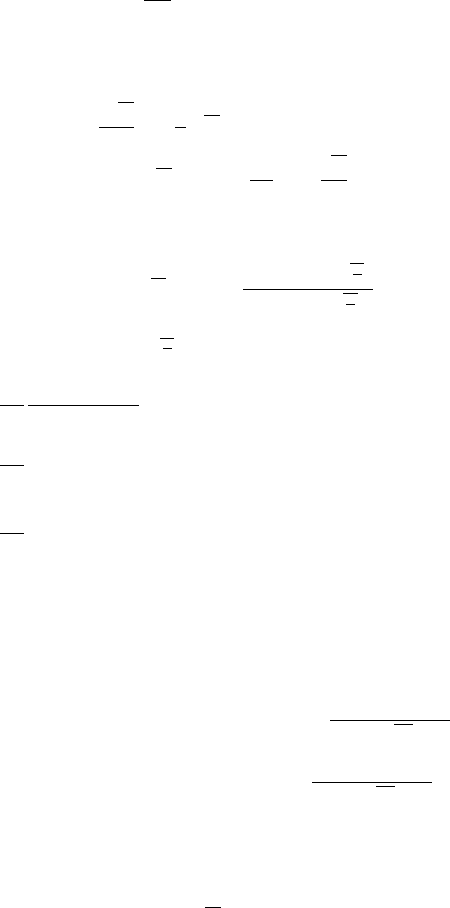
484 12 Integral Transform Methods with Applications
C
t
= κC
zz
, 0 <z<a, t>0, (12.11.49)
and the initial and boundary data
C (z, 0) = 0 for 0 <z<a, (12.11.50)
C (z, t)=C
0
for z = a, t > 0, (12.11.51)
∂C
∂z
=0 for z =0,t>0, (12.11.52)
where C
0
is a constant.
Application of the Laplace transform of C (z, t) with respect to t gives
d
2
C
dz
2
−
s
κ
C =0, 0 <z<a,
C (a, s)=
C
0
s
,
d
C
dz
z=0
=0.
The solution of this differential equation system is
C (z, s)=
C
0
cosh
z
s
κ
s cosh
a
s
κ
, (12.11.53)
which, by writing α =
s
κ
,
=
C
0
s
(e
αz
+ e
−αz
)
(e
αa
+ e
−αa
)
=
C
0
s
[exp {−α (a − z)} +exp{−α (a + z)}]
∞
n=0
(−1)
n
exp (−2nαa)
=
C
0
s
∞
n=0
(−1)
n
exp [−α {(2n +1)a − z}]
+
∞
n=0
(−1)
n
exp [−α {(2n +1)a + z}]
.(12.11.54)
Using the result (12.9.1), we obtain the final solution
C (z, t)=C
0
/
∞
n=0
(−1)
n
erfc
(2n +1)a − z
2
√
κt
+erfc
(2n +1)a + z
2
√
κt
. (12.11.55)
This solution represents an infinite series of complementary error functions.
The successive terms of this series are, in fact, the concentrations at depth
a −z, a + z,3a −z,3a + z, ... in the medium. The series converges rapidly
for all except large values of
κt
a
2
.
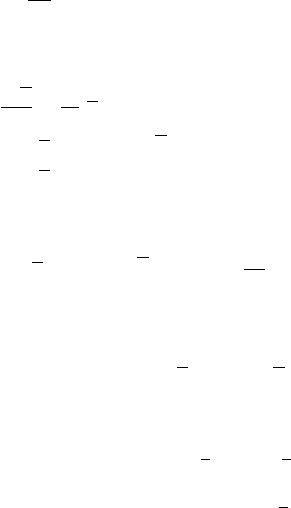
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 485
Example 12.11.10. (The Wave Equation for the Transverse Vibration of a
Semi-Infinite String). Find the displacement of a semi-infinite string, which
is initially at rest in its equilibrium position. At time t =0,theendx =0is
constrained to move so that the displacement is u (0,t)=Af(t)fort ≥ 0,
where A is a constant. The problem is to solve the one-dimensional wave
equation
u
tt
= c
2
u
xx
, 0 ≤ x<∞,t>0, (12.11.56)
with the boundary and initial conditions
u (x , t)=Af(t)atx =0,t≥ 0, (12.11.57)
u (x , t) → 0asx →∞,t≥ 0, (12.11.58)
u (x , t)=0=
∂u
∂t
at t =0 for 0<x<∞. (12.11.59)
Application of the Laplace transform of u (x, t) with respect to t gives
d
2
u
dx
2
−
s
2
c
2
u =0, for 0 ≤ x<∞,
u (x , s)= A f (s)atx =0,
u (x , s) → 0asx →∞.
The solution of this differential equation system is
u (x , s)=A f (s)exp
−
xs
c
. (12.11. 60)
Inversion gives the solution
u (x , t)=Af
t −
x
c
H
t −
x
c
. (12.11.61)
In other word s, the solution is
u (x , t)=
⎧
⎨
⎩
Af
t −
x
c
,t>
x
c
0,t<
x
c
.
(12.11.62)
This solution represents a wave propagating at a velocity c with the char-
acteristic x = ct.
Example 12.11.11. (The Cauchy–Poisson Wave Problem in Fluid Dynam-
ics). We consider the two-dimensional Cauchy–Poisson problem (Debnath
1994) for an inviscid liquid of infinite depth with a horizontal free surface.
We assume that the liquid has constant density ρ and negligible surface
tension. Waves are generated on the free surface of liquid initially at rest
for time t<0 by the prescribed free surface displacement at t =0.
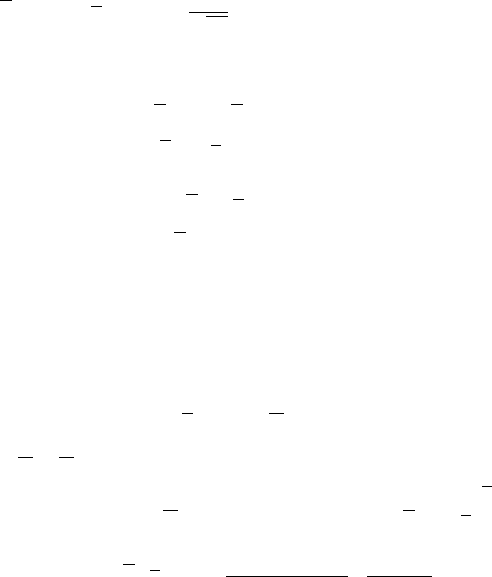
486 12 Integral Transform Methods with Applications
In terms of the velocity potential φ (x, z, t) and the free surface elevation
η (x, t), the linearized surface wave motion in Cartesian coordinates (x, y, z)
is governed by the following equation and free surface and boundary con-
ditions:
∇
2
φ = φ
xx
+ φ
zz
=0, −∞ <z≤ 0,x∈ R, t < 0, (12.11.63)
φ
z
− η
t
=0
φ
t
+ gη =0
on z =0,t>0, (12.11.64)
φ
z
→ 0asz →−∞. (12.11.65)
The initial conditions are
φ (x, 0, 0) = 0 and η (x, 0) = η
0
(x) , (12.11.66)
where η
0
(x) is a given initial elevation with compact support.
We introduce the Laplace transform with respect to t and the Fourier
transform with respect to x defined by
"
˜
φ (k, z , s) ,
˜
η (k, s)
#
=
1
√
2π
∞
−∞
e
−ikx
dx
∞
0
e
−st
[φ, η] dt. (12.11.67)
Application of the joint transform method to the above system gives
˜
φ
zz
− k
2
˜
φ =0, −∞ <z≤ 0, (12.11.68)
˜
φ = s
˜
η − ˜η
0
(k)
s
˜
φ + g
˜
η =0
⎫
⎪
⎬
⎪
⎭
on z =0, (12.11.69)
˜
φ
z
→ 0as z →−∞, (12.11.70)
where
˜η
0
(k)=F{η
0
(x)}.
The bounded solution of equation (12.11.68) is
˜
φ (k, s)=A exp (|k|z) , (12.11.71)
where A = A (s) is an arbitrary function of s.
Substituting (12.11.71) into (12.11.69) and eliminating
˜
η from t he re-
sulting equations gives
A. Hence, the solutions for
˜
φ and
˜
η are
"
˜
φ,
˜
η
#
=
−
g ˜η
0
exp (|k|z)
s
2
+ ω
2
,
s ˜η
0
s
2
+ ω
2
, (12.11.72)
and the associated the dispersion relation is
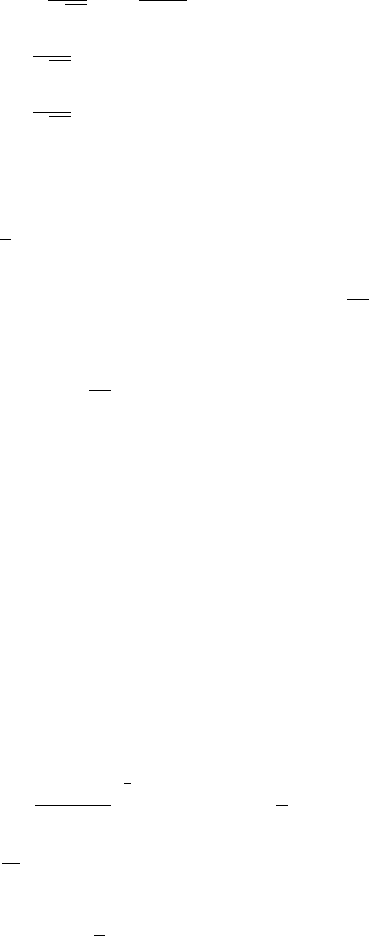
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 487
ω
2
= g |k|. (12.11.73)
The inverse Laplace and Fourier transforms give the solutions
φ (x, z, t)=−
g
√
2π
∞
−∞
sin ωt
ω
exp (ikx + |k|z)˜η
0
(k) dk, (12.11.74)
η (x, t)=
1
√
2π
∞
−∞
˜η
0
(k)cosωt e
ikx
dk,
=
1
√
2π
∞
0
˜η
0
(k)
"
e
i(kx−ωt)
+ e
i(kx+ωt)
#
dk, (12.11.75)
in which ˜η
0
(−k)=˜η
0
(k) is assumed.
Physically, the first and second integrals of (12.11.75) represent waves
traveling in the positive and negative directions of x, respectively, with
phase velocity
ω
k
. These integrals describe superposition of all such waves
over the wavenumber spectrum 0 <k<∞.
For the classical Cauchy–Poisson wave problem, η
0
(x)=aδ (x), where
δ (x) is the Dirac delta function, so that ˜η
0
(k)=
a/
√
2π
. Thus, solution
(12.11.75) becomes
η (x, t)=
a
2π
∞
0
"
e
i(kx−ωt)
+ e
i(kx+ωt)
#
dk. (12.11.76)
The wave integrals (12.11.74) and (12.11.75) represent the exact solution
for the velocity potential φ and the free surface elevation η for all x and
t>0. However, they do not lend any physical interpretations. In general,
the exact evaluation of these integrals is a formidable task. So it is necessary
to resort to asymptotic methods. It would be sufficient for the determination
of the princip al features of the wave motions to investigate (12.11.75) or
(12.11.76) asymptotically for large time t and large distance x with (x, t)
held fixed. The asymptotic solution for this kind of problem is available
in many standard books; (for example, see Debnath 1994, p. 85). We use
the stationary phase approximation of a typical wave integral (12.7.1), for
t →∞, given by (12.7.8)
η(x, t)=
b
a
F (k)exp[itθ(k)]dk (12.11.77)
∼ f(k
1
)
2π
t |θ
′′
(k
1
)|
1
2
exp
"
i
(
tθ(k
1
)+
π
4
sgn θ
′′
(k
1
)
)#
, (12.11.78)
where θ (k)=
kx
t
− ω (k), x>0, and k = k
1
is a stationary point that
satisfies the equation
θ
′
(k
1
)=
x
t
− ω
′
(k
1
)=0,a<k
1
<b. (12.11.79)
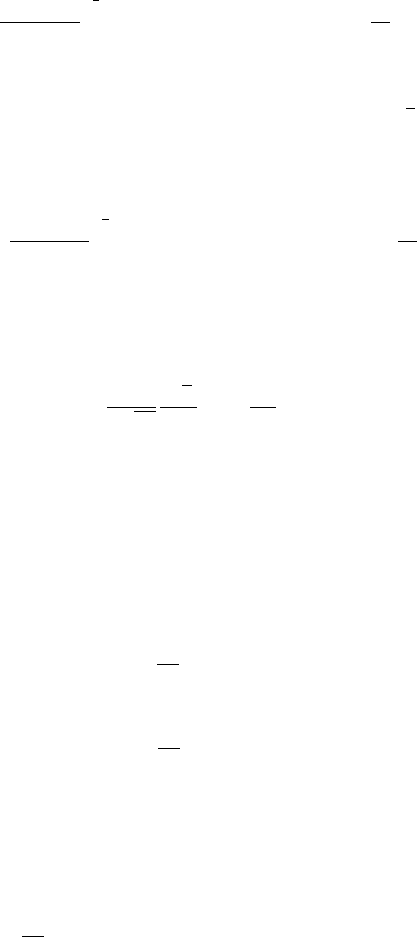
488 12 Integral Transform Methods with Applications
Application of (12.11.78) to (12.11.75) shows that only the first integral
in (12.11.75) has a stationary point for x>0. Hence, the stationary phase
approximation (12.11.78) gives the asymptotic solution, as t →∞, x>0,
η(x, t) ∼
1
t |ω
′′
(k
1
)|
1
2
˜η
0
(k
1
)exp
i{k
1
x − tω(k
1
)} +
iπ
4
sgn {−ω
′′
(k
1
)}
,
(12.11.80)
where k
1
=
gt
2
/4x
2
is the root of the equation ω
′
(k)=
x
t
.
On the other hand, when x<0, only the second integral of (12.11.75)
has a stationary point k
1
=
gt
2
/4x
2
, and hence, the same result (12.11.78)
can be used to obtain the asymptotic solution for t →∞and x<0as
η(x, t) ∼
1
t |ω
′′
(k
1
)|
1
2
˜η
0
(k
1
)exp
i {tω(k
1
) − k
1
|x|} +
iπ
4
sgn ω
′′
(k
1
)
.
(12.11.81)
In particular, for the classical Cauchy–Poisson solution (12.11.76), the
asymptotic representation for η (x, t) follows from (12.11.81) in the form
η (x, t) ∼
at
2
√
2π
√
g
x
3/2
cos
gt
2
4x
,gt
2
≫ 4x (12.11.82)
and gives a similar result for η (x, t), when x<0andt →∞.
12.12 Hankel Transforms
We introduce the definition of the Hankel transform from the two-dimen-
sional Fourier transform and its inverse given by
F{f (x, y)} = F (k, l)=
1
2π
∞
−∞
∞
−∞
exp {−i (κ
κ
κ · r)}f (x, y) dx dy,
(12.12.1)
F
−1
{F (k, l)} = f (x, y)=
1
2π
∞
−∞
∞
−∞
exp {i (κ
κ
κ · r)}F (k, l) dk dl,
(12.12.2)
where r =(x , y)andκ
κ
κ =(k, l). Introducing polar coordinates (x, y)=
r (cos θ, sin θ)and(k, l)=κ (cos φ, sin φ), we find κ
κ
κ · r = κr cos (θ − φ)and
then
F (κ, φ)=
1
2π
∞
0
rdr
2π
0
exp [−iκr cos (θ − φ)] f (r, θ) dθ. (12.12.3)

12.12 Hankel Transforms 489
We next assume f (r, θ)=exp(inθ) f (r), which is not a very severe
restriction, and make a change of variable θ −φ = α −
π
2
to reduce (12.12.3)
to the form
F (κ, φ)=
1
2π
∞
0
rf (r) dr
×
2π +φ
0
φ
0
exp
"
in
φ −
π
2
+ i (nα − κr sin α)
#
dα, (12.12.4)
where φ
0
=
π
2
− φ.
We use the integral representation of the Bessel function of order n
J
n
(κr)=
1
2π
2π +φ
0
φ
0
exp [i (nα − κr sin α)] dα (12.12.5)
so that integral (12.12.4) becomes
F (κ, φ)=exp
"
in
φ −
π
2
#
∞
0
rJ
n
(κr) f (r) dr (12.12.6)
=exp
"
in
φ −
π
2
#
˜
f
n
(κ) , (12.12.7)
where
˜
f
n
(κ) is called the Hankel transform of f (r) and is defined formally
by
H
n
{f (r)} =
˜
f
n
(κ)=
∞
0
rJ
n
(κr) f (r) dr. (12.12.8)
Similarly, in terms of the polar variables with the assumption f (x, y)=
f (r, θ)=e
inθ
f (r) and with result (12.12.7), the inverse Fourier transform
(12.12.2) becomes
e
inθ
f (r)=
1
2π
∞
0
κdκ
2π
0
exp [iκr cos (θ − φ)] F (κ, φ) dφ
=
1
2π
∞
0
κ
˜
f
n
(κ) dκ
2π
0
exp
"
in
φ −
π
2
+ iκr cos (θ − φ)
#
dφ,
which is, by the change of variables θ −φ = −
α +
π
2
and θ
0
= −
θ +
π
2
,
=
1
2π
∞
0
κ
˜
f
n
(κ) dκ
2π +θ
0
θ
0
exp [in (θ + α) − iκr sin α] dα
= e
inθ
∞
0
κJ
n
(κr)
˜
f
n
(κ) dκ, by (12.12.5). (12.12.9)
Thus, the inverse Hankel transform is defined by
H
−1
n
"
˜
f
n
(κ)
#
= f (r)=
∞
0
κJ
n
(κr)
˜
f
n
(κ) dκ. (12.12.10)

490 12 Integral Transform Methods with Applications
Instead of
˜
f
n
(κ), we often simply write
˜
f (κ) for the Hankel transform
specifying the order. Integrals (12.12.8) and (12.12.10) exist for certain
large classes of functions, which usually occur in physical applications.
Alternatively, the famous Hankel integral formula (Watson, 1966, p 453)
f (r)=
∞
0
κJ
n
(κr) dκ
∞
0
pJ
n
(κp) f (p) dp, (12.12.11)
can be used to define the Hankel transform (12.12.8) and its inverse
(12.12.10).
In particular, the Han kel transforms of zero order (n = 0) and of order
one (n = 1) are often useful for the solution of problems involving Laplace’s
equation in an axisymmetric cylindrical geometry.
Example 12.12.1. Obtain the zero-order Hankel transforms of
(a) r
−1
exp (−ar) , (b)
δ ( r)
r
, (c) H (a − r) ,
where H (r) is the Heaviside unit step function.
(a)
5
f
0
(κ)=H
0
&
1
r
exp (−ar)
'
=
∞
0
exp (−ar) J
0
(κr) dr =
1
√
κ
2
+a
2
.
(b)
5
f
0
(κ)=H
0
(
δ ( r)
r
)
=
∞
0
δ (r) J
0
(κr) dr =1.
(c)
5
f
0
(κ)=H
0
{H (a − r)} =
a
0
rJ
0
(κr) dr =
1
κ
2
aκ
0
pJ
0
(p) dp
=
1
κ
2
[pJ
1
(p)]
aκ
0
=
a
κ
J
1
(aκ) .
Example 12.12.2. Find the first-order Hankel transform of the following
functions:
(a) f (r)=e
−ar
, (b) f (r)=
1
r
e
−ar
.
(a)
˜
f (κ)=H
1
{e
−ar
} =
∞
0
re
−ar
J
1
(κr) dr =
κ
(a
2
+κ
2
)
3
2
.
(b)
˜
f (κ)=H
1
(
e
−ar
r
)
=
∞
0
e
−ar
J
1
(κr) dr =
1
κ
"
1 − a
κ
2
+ a
2
−
1
2
#
.
Example 12.12.3. Find the nth-order Hankel transforms of
(a) f (r)=r
n
H (a − r) , (b ) f (r)=r
n
exp
−ar
2
.
