Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 471
L[H (t − a) f (t − a)] =
∞
0
e
−(ξ+a)s
f (ξ) dξ
= e
−as
∞
0
e
−ξs
f (ξ) dξ = e
−as
¯
f (s) .
To prove (b), we write
L{H (t − a) g (t)} =
∞
a
e
−st
g (t) dt (t − a = τ)
=
∞
0
e
−s(a+τ)
g (a + τ) dτ = e
−sa
L{g (t + a)}.
Example 12.11.1. (a) Given that
f (t)=
⎧
⎨
⎩
0,t<2
t − 2,t≥ 2
⎫
⎬
⎭
=(t − 2) H (t − 2) ,
find the Laplace transform of f (t).
We have
L[f (t)] = L[H (t − 2) (t − 2)] = e
−2s
L[t]=
1
s
2
e
−2s
.
(b) Find the inverse Laplace transform of
f (s)=
1+e
−2s
s
2
.
L
−1
f (s)
!
= L
−1
1
s
2
+
e
−2s
s
2
= L
−1
1
s
2
+ L
−1
e
−2s
s
2
= t + H (t − 2) (t − 2)
=
⎧
⎨
⎩
t, 0 ≤ t<2,
2(t − 1) ,t≥ 2.
The Laplace transform of the impulse function p (t)isgivenby
L[p (t)] =
∞
0
e
−st
p (t) dt
=
a+ε
a−ε
he
−st
dt
= h
−
e
−st
s
a+ε
a−ε
=
he
−as
s
e
εs
− e
−εs
=2
he
−as
s
sinh (εs) . (12.11.2)
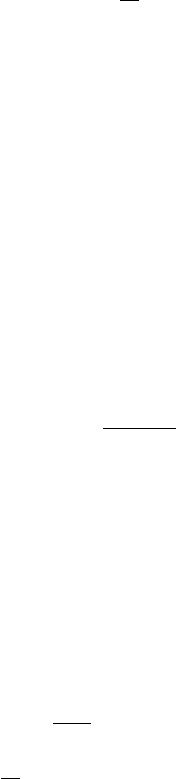
472 12 Integral Transform Methods with Applications
If we choose the value of h to be (1/2ε), then the impulse is given by
I (ε)=
∞
−∞
p (t) dt =
a+ε
a−ε
1
2ε
dt =1.
Thus, in the limit as ε → 0, this particular impulse function satisfies
lim
ε→0
p
ε
(t)=0,t= a,
lim
ε→0
I (ε)=1.
From this result, we obtain the Dirac delta function which satisfies
δ (t − a)=0,t= a,
∞
−∞
δ (t − a) dt =1. (12.11.3)
Thus, we may define the Laplace transform of δ (t) as the limit of the
transform of p
ε
(t).
L[δ (t − a)] = lim
ε→0
L[p
ε
(t)] ,
= lim
ε→0
e
−as
sinh (εs)
εs
(12.11.4)
= e
−as
.
If a =0,wehave
L[δ (t)]=1. (12.11.5)
One very useful result that can be derived is the integral of the pro d uct
of the delta function and any continuous function f (t).
∞
−∞
δ (t − a) f (t) dt = lim
ε→0
∞
−∞
p
ε
(t) f (t) dt,
= lim
ε→0
a+ε
a−ε
f (t)
2ε
dt,
= lim
ε→0
1
2ε
· 2εf (t
∗
) ,a− ε<t
∗
<a+ ε
= f (a) . (12.11.6)
Suppose that f (t) is a periodic function with period T .Letf be piece-
wise continuous on [0,T]. Then, the Laplace transform of f (t)is
L[f (t)] =
∞
0
e
−st
f (t) dt,
=
∞
n=0
(n+1)T
nT
e
−st
f (t) dt.
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 473
If we introduce a new variable ξ = t − nT ,then
L[f (t)] =
∞
n=0
e
−nT s
T
0
e
−sξ
f (ξ) dξ,
=
∞
n=0
e
−nT s
f
1
(s) ,
where
f
1
(s)=
*
T
0
e
−sξ
f (ξ) dξ is the transform of the function f over the
first period. Since the series is a geometric series, we obtain for the transform
of a periodic function
L[f (t)] =
f
1
(s)
(1 − e
−Ts
)
. (12.11.7)
Example 12.11.2. Find the Laplace transform of the square wave function
with period 2c given by
f (t)=
⎧
⎨
⎩
h, 0 <t<c
−h, c<t<2c
with f (t +2c)=f (t) ,
as shown in Fi gure 12.11.1.
Figure 12.11.1 Square wave function.

474 12 Integral Transform Methods with Applications
f
1
(s)=
2c
0
e
−sξ
f (ξ) dξ,
=
c
0
e
−sξ
hdξ +
2c
c
e
−sξ
(−h) dξ,
=
h
s
1 − e
−cs
2
.
Thus, the Laplace tran sform of f (t) is, by (12.11.7),
L[f (t)] =
f
1
(s)
1 − e
−2cs
=
h (1 − e
−cs
)
2
s (1 − e
−2cs
)
=
h (1 − e
−cs
)
s (1 + e
−cs
)
=
h
s
tanh
cs
2
.
Example 12.11.3. A uniform bar of length l is fixed at one end. Let the force
f (t)=
⎧
⎨
⎩
f
0
,t>0
0,t<0
be suddenly applied at the end x = l. If the bar is initially at rest, find the
longitudinal displacement for t>0.
The motion of the bar is governed by the differential system
u
tt
= a
2
u
xx
, 0 <x<l, t>0,a= constant,
u (x , 0) = 0,u
t
(x, 0) = 0,
u (0,t)=0,u
x
(l, t)=(f
0
/E) , where E is a constant and t>0.
Let
u (x , s) be the Laplace transform of u (x, t). Then, u (x, s) satisfies the
system
u
xx
−
s
2
a
2
u =0,
u (0,s)=0, u
x
(l, s)=(f
0
/Es) .
The solution of this differential equation is
u (x , s)=Ae
xs/a
+ Be
−xs/a
.
Applying the boundary conditions, we have
A + B =0,
s
a
e
ls/a
A +
−
s
a
e
−ls/a
B = f
0
/Es.
Solving for A and B, we obtain
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 475
A = −B =
af
0
Es
2
e
ls/a
+ e
−ls/a
.
Hence, the transform of the displacement function is given by
u (x , s)=
af
0
e
xs/a
− e
−xs/a
Es
2
e
ls/a
+ e
−ls/a
.
Before finding the inverse transform of
u (x , s), multiply the numerator and
denominator by
e
−ls/a
− e
−3ls/a
.Thus,wehave
u (x , s)=
af
0
Es
2
"
e
−(l−x)s/a
− e
−(l+x)s/a
− e
−(3l−x)s/a
+ e
−(3l+x)s/a
#
×
1
1 − e
−4ls/a
.
Since the denominator has the term
1 − e
−4ls/a
, the inverse transform
u (x , t) is periodic with period (4l/a). Hence, the final solution may be
writtenintheform
u (x , t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
0, 0 <t<
l−x
a
,
af
0
E
t −
l−x
a
,
l−x
a
<t<
l+x
a
,
af
0
E
t −
l−x
a
−
t −
l+x
a
!
,
l+x
a
<t<
3l−x
a
,
af
0
E
t −
l−x
a
−
t −
l+x
a
−
t −
3l−x
a
!
,
3l−x
a
<t<
3l+x
a
,
af
0
E
t −
l−x
a
−
t −
l+x
a
−
t −
3l−x
a
+
t −
3l+x
a
!
,
0,
3l+x
a
<t<
4l
a
,
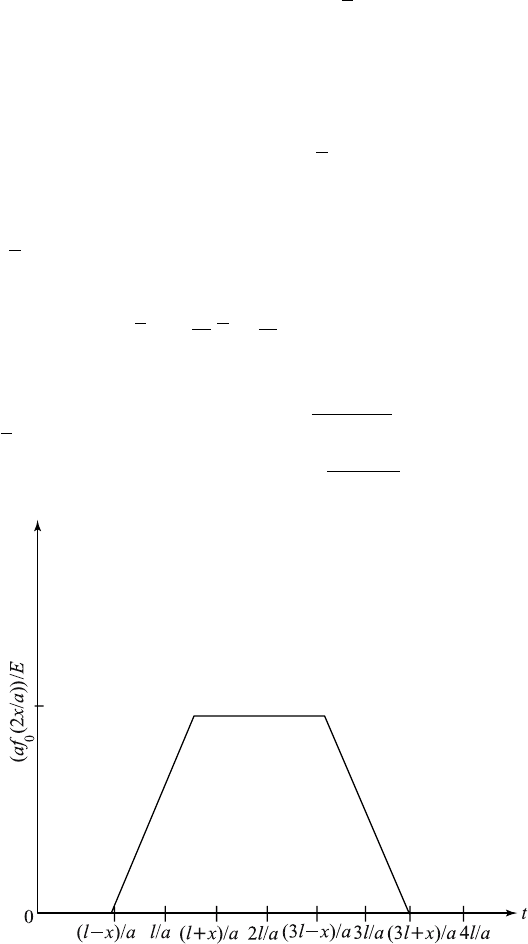
which may be simplified to obtain
u (x , t)=
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
0, 0 <t<(l − x) /a,
af
0
E
t −
l−x
a
, (l − x) /a < t < (l + x) /a,
af
0
E
2x
a
, (l + x) /a < t < (3l − x) /a,
af
0
E
−t +
3l+x
a
, (3l − x) /a < t < (3l + x) /a,
0, (3l + x) /a < t < 4l/a.
This result can clearly be seen in Figure 12.11.2.
476 12 Integral Transform Methods with Applications
Example 12.11.4. Consider a semi-infinite string fixed at the end x =0.
The string is initially at rest. Let there be an external force
f (x, t)=−f
0
δ
t −
x
v
,
acting on the string. This is a concentrated force f
0
acting at the point
x = vt.
The motion of the string is governed by the initial boundary-value prob-
lem
u
tt
= c
2
u
xx
− f
0
δ
t −
x
v
,
u (x , 0) = 0,u
t
(x, 0) = 0,
u (0,t)=0,u(x, t) is bounded as x →∞.
Let
u (x , s) be the Laplace transform of u (x, t). Transforming the wave
equation and using the initial conditions, we obtain
u
xx
−
s
2
c
2
u =
f
0
c
2
exp (−xs/v) .
The solution of this equation is
u (x , s)=
Ae
sx/c
+ Be
−sx/c
+
⎧
⎪
⎨
⎪
⎩
f
0
v
2
e
−sx/v
(c
2
−v
2
)s
2
for v = c,
−
f
0
xe
−sx/v
2cs
for v = c.
Figure 12.11.2 Graph of u (x, t).
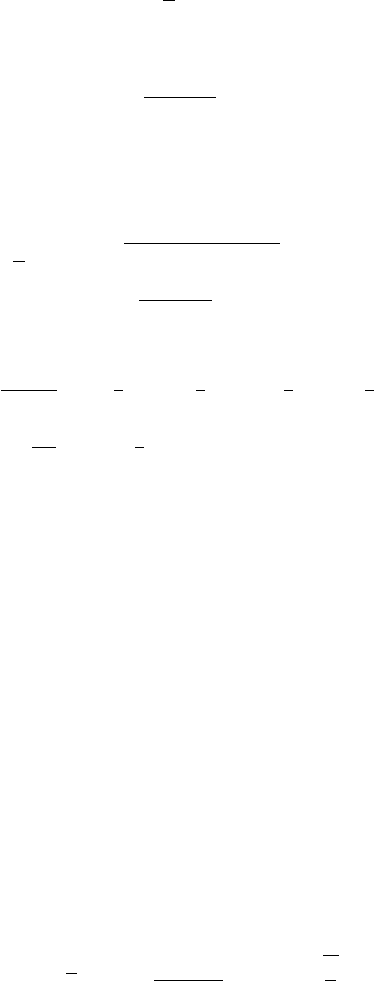
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 477
The condition that u (x, t) must be bounded at infinity requires that A =0.
Application of the condition
u (0,s)=0,
yields
B =
⎧
⎨
⎩
−f
0
v
2
(c
2
−v
2
)s
2
for v = c,
0forv = c.
Hence, the Laplace transform is given by
u (x , s)=
⎧
⎪
⎨
⎪
⎩
f
0
v
2
(
e
−xs/v
−e
−xs/c
)
(c
2
−v
2
)s
2
for v = c,
−
f
0
xe
−xs/c
2cs
for v = c.
The inverse Laplace transform is therefore given by
u (x , t)=
⎧
⎪
⎨
⎪
⎩
f
0
v
2
(c
2
−v
2
)
t −
x
v
u
t −
x
v
−
t −
x
c
u
t −
x
c
!
, f or v = c,
−
f
0
x
2c
u
t −
x
c
, for v = c.
Example 12.11.5. (The Stokes Problem and the Rayleigh Problem in fluid
dynamics). Solve the Stokes problem which is concerned with th e un steady
boundary layer flows induced in a semi-infinite viscous fluid bounded by an
infinite horizontal disk at z = 0 due to oscillations of the disk in its own
plane with a given frequency ω.
We solve the boundary layer equation for the velocity u (z, t)
u
t
= νu
zz
,z>0,t>0,
with the boundary and initial conditions
u (z, t)=U
0
e
iω t
,z=0,t>0,
u (z, t) → 0, as z →∞,t>0,
u (z, 0) = 0, at t ≤ 0 for all z>0,
where u (z, t) is the velocity of fluid of kinematic viscosity ν and U
0
is a
constant.
The Laplace transform solution of the equation with the transformed
boundary conditions is
u (z, s)=
U
0
(s − iω)
exp
−z
s
ν
.

478 12 Integral Transform Methods with Applications
Using a standard table of inverse Laplace transforms, we obtain the solution
u (z, t)=
U
0
2
e
iω t
"
exp (−λz)erfc
ζ −
√
iωt
+exp(λz)erfc
ζ +
√
iωt
#
,
where ζ =
z/2
√
νt
is called the similarity variable of the viscous boundary
layer theory, and λ =(iω/ν)
1
2
. This result describes the unsteady b ou ndar y
layer flow.
In view of the asymptotic formula for the complementary error function
erfc
ζ
+
√
iωt
∼ (2, 0) as t →∞,
the above solution for u (z, t) has the asymptotic representation
u (z, t) ∼ U
0
exp (iωt − λz)
= U
0
exp
iωt −
ω
2ν
1
2
(1 + i) z
. (12.11.8)
This is called the Stokes steady-state solution. This represents the prop-
agation of shear waves which spread out from the oscillating disk with
velocity ω/k =
√
2νω
k =(ω/2ν)
1
2
and exponentially decaying ampli-
tude. The boundary layer associated with the solution has thickness of the
order (ν/ω)
1
2
in which the shear oscillations imposed by the disk decay
exponentially with distance z from the disk. This boundary layer is called
the Stokes layer. In other words, the thickness of the Stokes layer is equal
to the depth of penetration of vorticity which is essentially confined to the
immediate vicinity of the disk for high frequency ω.
The Stokes problem with ω = 0 becomes the Rayleigh problem. In other
words, the motion is generated in the fluid from rest by moving the disk
impulsively in its own plane with constant velocity U
0
. In this case, the
Laplace transform solution is
u (z, s)=
U
0
s
exp
−z
s
ν
,
so that the inversion gives the Rayleigh solution
u (z, t)=U
0
erfc
z
2
√
νt
. (12.11.9)
This describes the growth of a boundary layer adjacent to the disk. The
associated boundary layer is called the Rayleigh layer of thickness of the
order δ ∼
√
νt which grows with increasing time t. The rate of gr owth is of
the order dδ/dt ∼
ν/t, which diminishes with increasing time.
12.11 Laplace Transforms of the Heaviside and Dirac Delta Functions 479
The vorticity of the unsteady flow is given by
∂u
∂z
=
U
0
√
πν t
exp
−ζ
2
(12.11.10)
which decays exponentially to zero as z ≫ δ.
Note that the vorticity is everywhere zero at t = 0 except at z =0.
This implies that i t is generated at the disk and diffuses outward within
the Rayleigh layer. The total viscous diffusion time is T
d
∼ δ
2
/ν.
Another physical quantity related to the Stokes and Rayleigh problems
is the skin friction on the disk defined by
τ
0
= µ
∂u
∂z
z=0
, (12.11.11)
where µ = νρ is the dynamic viscosity and ρ is the density of the fluid. The
skin friction can readily be calculated from the flow field given by (12.11.8)
or (12.11.9).
Example 12.11.6. (The Nonhomogeneous Cauchy Problem for the Wave
Equation). We consider the nonhomogeneous Cauchy problem
u
tt
− c
2
u
xx
= q (x, t) ,x∈ R, t > 0, (12.11.12)
u (x , 0) = f (x) ,u
t
(x, 0) = g (x) for all x ∈ R, (12.11.13)
where q (x, t) is a given function representing a source term.
We use the joint Laplace and Fourier transform of u (x, t)
U (k, s)=L[F{u (x, t)}]=
1
√
2π
∞
−∞
e
−ikx
dx
∞
0
e
−st
u (x , t) dt.
(12.11.14)
Application of the joint t ransfor m leads to the solution of the trans-
formed Cauchy problem in th e form
U (k, s)=
sF(k)+G (k)+
Q (k, s)
(s
2
+ c
2
k
2
)
. (12.11.15)
The inverse Laplace transform of (12.11.15) gives
U (k, t)=F (k) cos (ckt)+
1
ck
G (k)sin(ckt)+
1
ck
L
−1
ck
s
2
+ c
2
k
2
·
Q (k, s)
= F (k) cos (ckt)+
G (k)
ck
sin (ckt)+
1
ck
t
0
sin ck (t − τ ) Q (k, τ) dτ.
(12.11.16)
The inverse Fourier transform leads to the exact integral solution

480 12 Integral Transform Methods with Applications
u (x , t)=
1
2
√
2π
∞
−∞
e
ickt
+ e
−ickt
e
ikx
F (k) dk
+
1
2
√
2π
∞
−∞
e
ickt
− e
−ickt
e
ikx
·
G (k)
ick
dk
+
1
√
2π
·
1
2c
t
0
dτ
∞
−∞
Q (k, τ)
ik
"
e
ick(t−τ )
− e
−ick(t−τ )
#
e
ikx
dk
=
1
2
[f (x + ct)+f (x − ct)] +
1
2c
x+ct
x−ct
g (ξ) dξ
+
1
2c
t
0
dτ
1
√
2π
∞
−∞
Q (k, τ) dk
x+c(t−τ)
x−c(t−τ)
e
ikξ
dξ
=
1
2
[f (x − ct)+f (x + ct)] +
1
2c
x+ct
x−ct
g (ξ) dξ
+
1
2c
t
0
dτ
x+c(t−τ)
x−c(t−τ)
q (ξ,τ ) dξ. (12.11.17)
In the case of the homogeneous Cauchy problem, q (x, t) ≡ 0, the solution
of (12.11.17) reduces to the famous d’Alembert solution (5.3.8).
Example 12.11.7. (The Heat Conduction Equation in a Semi-Infinite Medium
and Fractional Derivatives). Solve the one-dimensional diffusion equation
u
t
= κu
xx
,x>0,t>0, (12.11.18)
with the initial and boundary conditions
u (x , 0) = 0,x>0, (12.11.19)
u (0,t)=f (t) ,t>0, (12.11.20)
u (x , t) → 0, as x →∞,t>0. (12.11.21)
Application of the Laplace transform with respect to t to (12.11.18)
gives
d
2
u
dx
2
−
s
κ
u =0. (12.11.22)
The general solution of this equation is
u (x , s)=A exp
−x
s
κ
+ B exp
x
s
κ
,
where A and B are integrating constants. For bounded solutions, B ≡ 0,
and using
u (0,s)=f (s), we obtain the solution
u (x , s)=f (s)exp
−x
s
κ
. (12.11.23)
