Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


12.8 Laplace Transforms 461
the Laplace transform and its inverse. We replace f (x) in (6.13.10) by
H (x) e
−cx
f (x)forx>0toobtain
f (x) H (x) e
−cx
=
1
2π
∞
−∞
e
ikx
dk
∞
0
f (t) e
−t(c+ik)
dt
or
f (x) H (x)=
1
2π
∞
−∞
e
x(c+ik)
dk
∞
0
f (t) e
−t(c+ik)
dt.
Substituting s = c + ik so that ds = idk, we obtain, for x>0,
f (x) H (x)=
1
2πi
c+i∞
c−i∞
e
xs
ds
∞
0
f (t) e
−st
dt. (12.8.1)
Thus, we give the following definition of the Laplace transform: If f (t)is
defined for all values of t>0, then the Laplace transform of f (t) is d enoted
by
¯
f (s)orL{f (t)} and is defined by the integral
¯
f (s)=L{f (t)} =
∞
0
e
−st
f (t) dt, (12.8.2)
where s is a positive real number or a complex number with a positive real
part so that the integral is convergent.
Hence, (12.8.1) gives
f (x)=L
−1
&
¯
f (s)
'
=
1
2πi
c+i∞
c−i∞
e
xs
¯
f (s) ds, c > 0, (12.8.3)
for x>0andzeroforx<0. This complex integral is used to define the
inverse Laplace transform whichisdenotedbyL
−1
&
¯
f (s)
'
= f (t). It can
be verified easily that both L and L
−1
are linear integral operators.
We now find the Laplace transforms of some elementary functions.
1. Let f (t)=c, c is a constant.
L[c]=
∞
0
e
−st
cdt
=
−
ce
−st
s
∞
0
=
c
s
.
2. Let f (t)=e
at
, a is a constant.
L
e
at
!
=
∞
0
e
−st
e
at
dt
=
−
e
−(s−a)t
(s − a)
∞
0
=
1
s − a
,s≥ a.
3. Let f (t)=t
2
.Then

462 12 Integral Transform Methods with Applications
L
t
2
!
=
∞
0
e
−st
t
2
dt.
Integration by parts yields
L
&
t
2
'
=
−
t
2
e
−st
s
∞
0
+
∞
0
e
−st
s
2 tdt.
Since t
2
e
−st
→ 0ast →∞, we have, integrating by parts again,
L
t
2
!
=
2
s
−
e
−st
s
t
+
2
s
∞
0
e
−st
s
dt =
2
s
3
.
4. Let f (t)=sinωt.
¯
f (s)=L[sin ωt]=
∞
0
e
−st
sin ωt dt
=
−
e
−st
s
sin ωt
∞
0
+
∞
0
e
−st
s
ω cos ωt dt
=
ω
s
−
e
−st
s
cos ωt
−
ω
s
∞
0
e
−st
s
ω sin ωt dt
¯
f (s)=
ω
s
2
−
ω
2
s
2
¯
f (s) .
Thus, solving for
¯
f (s), we obtain
L[sin ωt]=ω/
s
2
+ ω
2
.
A function f (t)issaidtobeofexponential order as t →∞if there
exist real constants M and a such that |f (t)|≤Me
at
for 0 ≤ t<∞.
Theorem 12.8.1. Let f be piecewise continuous in the interval [0,T] for
every positive T ,andletf be of exponential order, that is, f (t)=O (e
at
)
as t →∞for some a>0. Then, the Laplace transform of f (t) exists for
Re s>a.
Proof.Sincef is piecewise continuous and of exponential order, we have
|L(f (t))| =
∞
0
e
−st
f (t) dt
≤
∞
0
e
−st
|f (t)|dt
≤
∞
0
e
−st
Me
at
dt
= M
∞
0
e
−(s−a)t
dt = M/(s − a) , Re s>a.
Thus,
∞
0
e
−st
f (t) dt
exists for Re s>a.

12.9 Properties of Laplace Transforms 463
12.9 Properties of Laplace Transforms
Theorem 12.9.1. (Linearity) If L[f (t)]and L[g (t)] are Laplace trans-
forms of f (t) and g (t) respectively, then
L[af (t)+bg (t)] = a L[f (t)] + b L[g (t)]
where a and b are constants.
Proof.
L[af (t)+bg (t)] =
∞
0
[af (t)+bg (t)] e
−st
dt
= a
∞
0
f (t) e
−st
dt + b
∞
0
g (t) e
−st
dt
= a L[f (t)] + b L[g (t)] .
This shows that L is a linear operator.
Theorem 12.9.2. (Shifting) If
¯
f (s) is the Laplace transform of f (t),
then the Laplace transform of e
at
f (t) i s
¯
f (s − a).
Proof.Bydefinition,wehave
L
e
at
f (t)
!
=
∞
0
e
−st
e
at
f (t) dt
=
∞
0
e
−(s−a)t
f (t) dt
=
¯
f (s − a) .
Example 12.9.1.
(a) If L
t
2
!
=2/s
3
,thenL[t
s
e
t
]=2/ (s − 1)
3
.
(b) If L[sin ωt]=ω/
s
2
+ ω
2
,thenL[e
at
sin ωt]=ω/
"
(s − 1)
2
+ ω
2
#
.
(c) If L{cos ωt} =
s
s
2
+ω
2
,thenL{e
at
cos ωt} =
s−a
(s−a)
2
+ω
2
.
(d) If L{t
n
} =
n!
s
n+1
,thenL{e
at
t
n
} =
n!
(s−a)
n+1
.
Theorem 12.9.3. (Scaling) If the Laplace transform of f (t) is
¯
f (s), then
the Laplace transform of f (ct) with c>0 is (1/c)
¯
f (s/c).
Proof.Bydefinition,wehave
L[f (ct)] =
∞
0
e
−st
f (ct) dt
=
∞
0
1
c
e
−(sξ/c)
f (ξ) dξ (substituting ξ = ct)
=(1/c)
¯
f (s/c) .
464 12 Integral Transform Methods with Applications
Example 12.9.2.
(a) If
s
s
2
+1
= L[cos t], then
1
ω
s/ω
(s/ω)
2
+1
=
s
s
2
+ ω
2
= L[cos ωt] .
(b) If
1
s−1
= L[e
t
], then
1
a
1
s
a
− 1
= L
e
at
!
,
or
L
e
at
!
=
1
s − a
.
Theorem 12.9.4. (Differentiation)Letf be continuous and f
′
piecewise
continuous, in 0 ≤ t ≤ T for all T>0.Letf also be of exponential order
as t →∞. Then, the Laplace transform of f
′
(t) exists and is given by
L[f
′
(t)] = s L[f (t)] − f (0) = s
¯
f (s) − f (0) .
Proof. Consider the defin ite integral
T
0
e
−st
f
′
(t) dt =
e
−st
f (t)
!
T
0
+
T
0
se
−st
f (t) dt
= e
−sT
f (T ) − f (0) + s
T
0
e
−st
f (t) dt.
Since |f (t)|≤Me
at
for large t,witha>0andM>0,
e
−sT
f (T )
≤ Me
−(s−a)T
.
In the limit as T →∞, e
−sT
f (T ) → 0 whenever s>a. Hence,
L[f
′
(t)] = s L[f (t)] − f (0) = s
¯
f (s) − f (0) .
If f
′
and f
′′
satisfy the same conditions imposed on f an d f
′
respec-
tively, then, the Laplace transform of f
′′
(t) can be obtained immediately
by applying the preceding theorem; that is
L[f
′′
(t)] = s L[f
′
(t)] − f
′
(0)
= s {sL[f (t)] − f (0)}−f
′
(0)
= s
2
L[f (t)] − sf (0) − f
′
(0)
= s
2
¯
f (s) − sf (0) − f
′
(0) .
Clearly, the Laplace transform of f
(n)
(t) can be obtained in a similar man-
ner by successive application of Theorem 12.9.4. The result may be written
as
L
"
f
(n)
(t)
#
= s
n
L[f (t)] − s
n−1
f (0) − ...− sf
(n−2)
(0) − f
(n−1)
(0) .

12.9 Properties of Laplace Transforms 465
Theorem 12.9.5. (Integration)If
¯
f (s) is the Laplace transform of f (t),
then
L
t
0
f (τ) dτ
=
¯
f (s) /s.
Proof.
L
t
0
f (τ) dτ
=
∞
0
t
0
f (τ) dτ
e
−st
dt
=
−
e
−st
s
t
0
f (τ) dτ
∞
0
+
1
s
∞
0
f (t) e
−st
dt
=
¯
f (s) /s
since
t
0
f (τ) dτ is of exponential order.
In solving problems by the Laplace transform method, the difficulty
arises in finding inverse transforms. Although the inversion formula ex-
ists, its evaluation requires a knowledge of functions of complex variables.
However, for some problems of mathematical physics, we need not use this
inversion formula. We can avoid its use by expanding a given transform by
the method of partial fractions in terms of simple fractions in the trans-
form variables. With these simple functions, we refer to the table of Laplace
transforms given in the end of the book and obtain the inverse transforms.
Here, we should note that we use the assumption that there is essentially a
one-to-one correspondence between functions and their Laplace transforms.
This may be stated as follows:
Theorem 12.9.6. (Lerch)Letf and g be piecewise continuous functions
of exponential order. If there exists a constant s
0
, such that L[f]=L[g]
for all s>s
0
, then f (t)=g (t) for all t>0 except possibly at the points
of discontinuity.
For a proof, the reader is referred to Kreider et al. (1966).
In order to find a solution of linear partial differential equations, the
following formulas and results are useful.
If L{u (x, t)} =
u (x , s), then
L
∂u
∂t
= s
u (x , s) − u (x, 0) ,
L
∂
2
u
∂t
2
= s
2
u (x , s) − su(x, 0) − u
t
(x, 0) ,
and so on.
Similarly, it is easy to show that
466 12 Integral Transform Methods with Applications
L
∂u
∂x
=
d
u
dx
, L
∂
2
u
∂x
2
=
d
2
u
dx
2
,...,L
∂
n
u
∂x
n
=
d
n
u
dx
n
.
The following results are useful for applications:
L
erfc
a
2
√
t
=
1
s
exp
−a
√
s
,a≥ 0, (12.9.1)
L
(
exp (at)erf
√
at
)
=
√
a
√
s (s − a)
,a>0. (12.9.2)
Example 12.9.3. Consider the motion of a semi-infini te string with an ex-
ternal force f (t) acting on it. One end is kept fixed while the other end is
allowed to move freely in the vertical direction. If the string is initially at
rest, the motion of the string is governed by
u
tt
= c
2
u
xx
+ f (t) , 0 <x<∞,t>0,
u (x , 0) = 0,u
t
(x, 0) = 0,
u (0,t)=0,u
x
(x, t) → 0, as x →∞.
Let
u (x , s) be the Laplace transform of u (x, t). Transforming the equa-
tion of motion and using the initial conditions, we obtain
u
xx
−
s
2
/c
2
u = −f (s) /c
2
.
The solution of this ordinary differential equation is
u (x , s)=Ae
sx/c
+ Be
−sx/c
+
f (s) /s
2
!
.
The transformed boundary conditions are given by
u (0,s)=0, and lim
x→∞
u
x
(x, s)=0.
In view of the second condition, we have A = 0. Now applying the first
condition, we obtain
u (0,s)=B +
f (s) /s
2
!
=0.
Hence
u (x , s)=
f (s) /s
2
!
"
1 − e
−sx/c
#
.
(a) When f (t)=f
0
, a constant, then
u (x , s)=f
0
1
s
3
−
1
s
3
e
−sx/c
.
The inverse Laplace transform gives the solution
12.10 Convolution Theorem of the Laplace Transform 467
u (x , t)=
f
0
2
t
2
−
t −
x
c
2
when t ≥ x/c,
=(f
0
/2) t
2
when t ≤ x/c.
(b) When f (t)=cosωt,whereω is a constant , then
¯
f (s)=
∞
0
e
−st
cos ωt dt = s/
ω
2
+ s
2
.
Thus, we have
u (x , s)=
1
s (ω
2
+ s
2
)
1 − e
−sx/c
. (12.9.3)
By the method of partial fractions, we write
1
s (s
2
+ ω
2
)
=
1
ω
2
1
s
−
1
s
2
+ ω
2
.
Hence
L
−1
1
s (s
2
+ ω
2
)
=
1
ω
2
(1 − cos ωt)=
2
ω
2
sin
2
ωt
2
.
If we denote
ψ (t)=sin
2
ωt
2
,
then the Laplace inverse of equation (12.9.3) may be written in the form
u (x , t)=
2
ω
2
"
ψ (t) − ψ
t −
x
c
#
when t ≥ x/c,
=
2
ω
2
ψ (t)whent ≤ x/c.
12.10 Convolution Theorem of the Laplace Transform
The function
(f ∗g)(t)=
t
0
f (t − ξ) g (ξ) dξ (12.10.1)
is called the convolution of the functions f and g.
Theorem 12.10.1. (Convolution)If
¯
f (s) and ¯g (s) are the Laplace trans-
forms of f (t) and g (t) respectively, then the Laplace transform of the con-
volution (f ∗ g)(t) is the product
¯
f (s)¯g (s).
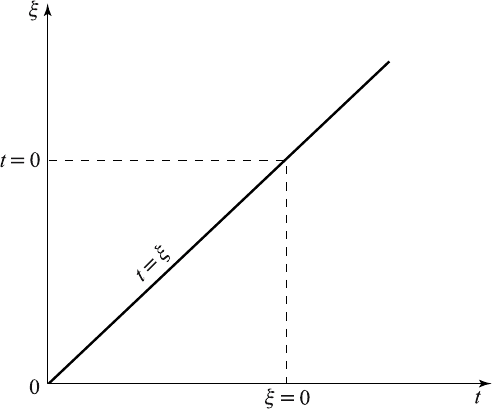
468 12 Integral Transform Methods with Applications
Figure 12.10.1 Region of integration.
Proof.Bydefinition,wehave
L[(f ∗ g)(t)] =
∞
0
e
−st
t
0
f (t − ξ) g (ξ) dξ dt
=
∞
0
t
0
e
−st
f (t − ξ) g (ξ) dξ dt.
The region of integration is shown in Figure 12.10.1. By reversing the order
of integration, we have
L[(f ∗ g)(t)] =
∞
0
∞
ξ
e
−st
f (t − ξ) g (ξ) dt dξ
=
∞
0
g (ξ)
t
ξ
e
−st
f (t − ξ) dt dξ.
If we introduce the new variable η =(t − ξ) in the inner integral, we obtain
L[(f ∗ g)(t)] =
∞
0
g (ξ)
∞
0
e
−s(ξ+η)
f (η) dη dξ
=
∞
0
g (ξ) e
−sξ
dξ
∞
0
e
−sη
f (η) dη
=
¯
f (s)¯g (s) . (12.10.2)
The convolution satisfies the following properties:
12.10 Convolution Theorem of the Laplace Transform 469
1. f ∗ g = g ∗ f (commutative).
2. f ∗ (g ∗ h)=(f ∗ g) ∗ h (associative).
3. f ∗ (αg + βh)=α (f ∗ g)+β (f ∗h) , (distributive),
where α and β are constants.
Example 12.10.1. Find the temperature distribution in a semi-infinite radi-
ating rod. The temperature is kept constant at x = 0, while the other end
is kept at zero temperature. If the initial temperature distribution is zero,
the problem is governed by
u
t
= ku
xx
− hu, 0 <x<∞,t>0,h= constant,
u (x , 0) = 0,u(0,t)=u
0
,t>0,u
0
= constant,
u (x , t) → 0, as x →∞.
Let
u (x , s) be the Laplace transform of u (x, t). Then the transformation
with respect to t yields
u
xx
−
s + h
k
u =0,
u (0,s)=u
0
/s, lim
x→∞
u (x , s)=0.
The solution of this equation is
u (x , s)=Ae
x
√
(s+h)/k
+ Be
−x
√
(s+h)/k
.
The boundary condition at infinity requires that A = 0. Applying the other
boundary condition gives
u (0,s)=B = u
0
/s.
Hence, the solution takes t he form
u (x , s)=(u
0
/s)exp
"
−x
(s + h) /k
#
.
We find (by using the Table of Laplace Transforms) that
L
−1
"
u
0
s
#
= u
0
,
and
L
−1
"
exp
(
−x
(s + h) /k
)#
=
x exp
−ht −
x
2
/4kt
!
2
√
πkt
3
.
Thus, the inverse Laplace transform of
u (x , s)is
u (x , t)=L
−1
"
u
0
s
exp
(
−x
(s + h) /k
)#
.
470 12 Integral Transform Methods with Applications
By the Integration Theorem 12.9.5, we have
u (x , t)=
t
0
u
0
x exp
−hτ −
x
2
/4kτ
!
2
√
πk τ
3
2
dτ.
Substituting the new variable η =
x/2
√
kτ
yields
u (x , t)=
2 u
0
√
π
∞
x/2
√
kt
exp
−η
2
+
hx
2
/4kη
2
!
dη.
For the case h = 0, the solution u (x, t) becomes
u (x , t)=
2 u
0
√
π
∞
x/2
√
kt
e
−η
2
dη
=
2 u
0
√
π
∞
0
e
−η
2
dη −
2 u
0
√
π
x/2
√
kt
0
e
−η
2
dη
= u
0
1 − erf
x
2
√
kt
= u
0
erfc
x
2
√
kt
.
12.11 Laplace Transforms of the Heaviside and Dirac
Delta Functions
We have defined the Heaviside unit step function. Now, we will find its
Laplace transform.
L[H (t − a)] =
∞
0
e
−st
H (t − a) dt
=
∞
a
e
−st
dt =
1
s
e
−as
,s>0. (12.11.1)
Theorem 12.11.1. (Second Shifting)If
¯
f (s) and ¯g (s) are the Laplace
transforms of f (t) and g (t) respectively, then
(a) L[H (t − a) f (t − a)] = e
−as
¯
f (s)=e
−as
L{f (t)}.
(b) L{H (t − a) g (t)} = e
−as
L{g (t + a)}.
Proof. (a) By d efini tion
L[H (t − a) f (t − a)] =
∞
0
e
−st
H (t − a) f (t − a) dt
=
∞
a
e
−st
f (t − a) dt.
Introducing the new variable ξ = t − a, we obtain
