Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


12.4 Convolution Theorem of the Fourier Transform 451
=
1
√
2π
∞
−∞
f (ξ) g (x − ξ) dξ,
where g (x) is the inverse transform of G (k)=e
−k
2
κt
and has the form
g (x)=F
−1
(
e
−κk
2
t
)
=
1
√
2π
∞
−∞
e
−k
2
κt+ikx
dk =
1
√
2κt
e
−x
2
/4κt
.
Consequently, the fin al solution is
u (x , t)=
1
√
4πκt
∞
−∞
f (ξ)exp
−
(x − ξ)
2
4κt
dξ, (12.4.11)
=
∞
−∞
f (ξ) G (x − ξ, t) dξ, (12.4.12)
where
G (x − ξ,t)=
1
√
4πκt
exp
−
(x − ξ)
2
4κt
, (12.4.13)
is called the Green’s function (or the fundamental solution) of the diffusion
equation.
This means that temperature at any point x an d any time t is repre-
sented by the definite integral (12.4.12) that is made up of the contribution
due to the initial source f (ξ) and the Green’s function G (x − ξ, t).
Solution (12.4.12) represents the temperature response along the rod at
time t due to an initial unit impulse of heat at x = ξ. The physical meaning
of the solution is that the initial temperature distribution f (x) is decom-
posed into a spectrum of impulses of magnitude f (ξ)ateachpointx = ξ to
form the resulting temperature f (ξ) G (x − ξ, t). Thus, the resulting tem-
perature is integrated to find the solution (12.4.11). This is the so-called
principle of superposition.
Using the change of variable
ξ − x
2
√
κt
= ζ, dζ =
dξ
2
√
κt
,
we obtain
u (x , t)=
1
√
π
∞
−∞
f
x +2
√
κt ζ
e
−ζ
2
dζ. (12.4.14)
Integral (12.4.11) or (12.4.14) is called the Poisson integral representa-
tion of the temperature distribution. This integral is convergent for t>0,
and integrals obtained from it by differentiation under the integral sign
with respect t o x and t are uniformly convergent in the neighborhood of
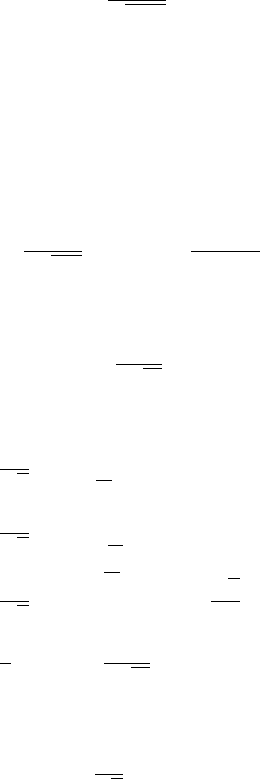
452 12 Integral Transform Methods with Applications
the point (x, t). Hence, u (x, t) and its derivatives of all orders exist for
t>0.
In the limit t → 0+, solution (12.4.12) becomes formally
u (x , 0) = f (x)=
∞
−∞
f (ξ) lim
t→0+
G (x − ξ,t) dξ.
This limit represents the Dirac delta function
δ (x − ξ) = lim
t→0+
1
√
4πκt
e
−(x−ξ)
2
/4κt
. (12.4.15)
Consider a special case where
f (x)=
⎧
⎨
⎩
0,x<0
a, x > 0
⎫
⎬
⎭
= aH(x) .
Then, the solution (12.4.11) gives
u (x , t)=
a
2
√
πκt
∞
0
exp
−
(x − ξ)
2
4κt
dξ.
If we introduce a change of variable
η =
ξ − x
2
√
κt
then the above solution becomes
u (x , t)=
a
√
π
∞
−x/2
√
κt
e
−η
2
dη
=
a
√
π
0
−x/2
√
κt
e
−η
2
dη +
∞
0
e
−η
2
dη
=
a
√
π
x/2
√
κt
0
e
−η
2
dη +
√
π
2
=
a
2
1+erf
x
2
√
κt
,
where erf (x) is called the error function andisdefinedby
erf (x)=
2
√
π
x
0
e
−η
2
dη. (12.4.16)
This is a widely used and tabulated function.
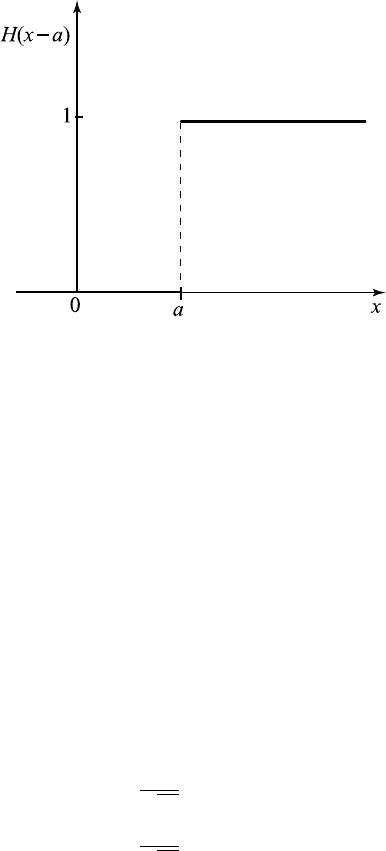
12.5 The Fourier Transforms of Step and Impulse Functions 453
Figure 12.5.1 The Heaviside unit step function.
12.5 The Fourier Transforms of Step and Impulse
Functions
In this section, we shall determine the Fourier tran sforms of the step func-
tion and the impulse function, functions which occur frequently in applied
mathematics and mathematical physics.
The Heaviside unit step function is defined by
H (x − a)=
⎧
⎨
⎩
0,x<a
1,x≥ a
a ≥ 0, (12.5.1)
as shown in Fi gure 12.5.1.
The Fourier transform of the Heaviside unit step function can be easily
determined. We consider first
F [H (x − a)] =
1
√
2π
∞
−∞
H (x − a) e
−ikx
dx,
=
1
√
2π
∞
a
e
−ikx
dx.
This integral does not exist. However, we can prove the existence of this
integral by defining a new function
H (x − a) e
−αx
=
⎧
⎨
⎩
0,x<a
e
−αx
,x≥ a.
This is evidently the unit step function as α → 0. Thus, we find the Fourier
transform of the unit step function as
454 12 Integral Transform Methods with Applications
Figure 12.5.2 Impulse function p (x).
F [H (x − a)] = lim
α→0
F
H (x − a) e
−αx
!
= lim
α→0
1
√
2π
∞
−∞
H (x − a) e
−αx
e
−ikx
dx
= lim
α→0
1
√
2π
∞
a
e
−(α+ik)x
dx
=
e
−iak
√
2πik
. (12.5.2)
For a =0,
F [H (x)] =
√
2πik
−1
. (12.5.3)
An impulse function is defined by
p (x)=
⎧
⎨
⎩
h, a − ε<x<a+ ε
0,x≤ a − ε or x ≥ a + ε
where h is large and positive, a>0, and ε is a small positive constant, as
shown in Figure 12.5.2. This type of function appears in practical applica-
tions; for instance, a force of large magnitude may act over a very short
period of time.
The Fourier transform of the impulse function is

12.5 The Fourier Transforms of Step and Impulse Functions 455
F [p (x)] =
1
√
2π
∞
−∞
p (x) e
−ikx
dx
=
1
√
2π
a+ε
a−ε
he
−ikx
dx
=
h
√
2π
e
−iak
ik
e
ikε
− e
−ikε
=
2hε
√
2π
e
−iak
sin kε
kε
.
Nowifwechoosethevalueofh to be (1/2ε), then the impulse defined by
I (ε)=
∞
−∞
p (x) dx
becomes
I (ε)=
a+ε
a−ε
1
2ε
dx =1
which is a constant independent of ε. In the limit as ε → 0, this particular
function p
ε
(x)withh =(1/2ε) satisfies
lim
ε→0
p
ε
(x)=0,x= a,
lim
ε→0
I (ε)=1.
Thus, we arrive at the result
δ (x − a)=0,x= a,
∞
−∞
δ (x − a) dx =1. (12.5.4)
This is the Dirac delta function which was defined earlier in Section 8.11.
We now define the Fourier transform of δ (x) as the limit of the transform
of p
ε
(x). We then consider
F [δ (x − a)] = lim
ε→0
F [p
ε
(x)]
= lim
ε→0
e
−iak
√
2π
sin kε
kε
=
e
−iak
√
2π
(12.5.5)
in which we note that, by L’Hospital’s rule, lim
ε→0
(sin kε/kε)=1.When
a = 0, we obtain
F [δ (x)] =
1/
√
2π
. (12.5.6)

456 12 Integral Transform Methods with Applications
Example 12.5.1. Slowing-down of Neutrons (see Sneddon (1951), p. 215).
Consider the followin g physical prob lem
u
t
= u
xx
+ δ (x) δ (t) , (12.5.7)
u (x , 0) = δ (x) , (12.5.8)
lim
|x|→∞
u (x , t)=0. (12.5.9)
This is the p rob lem of an infinite medium which slows neutrons, in which a
source of neutrons is located. Here u (x, t) represents the number of neutrons
per unit volume per unit time and δ (x) δ (t) represents the source function.
Let U (k, t) be the Fourier transform of u (x, t). Then the Fourier trans-
formation of equation (12.5.7) yields
dU
dt
+ k
2
U =
1
√
2π
δ (t) .
The solution of this, after applying the condition U (k, 0) =
1/
√
2π
,is
U (k, t)=
1
√
2π
e
−k
2
t
.
Hence, the inverse Fourier transform gives the solution of the problem
u (x , t)=
1
√
2π
∞
−∞
e
−k
2
t+ikx
dk,
=
1
√
4πt
e
−x
2
/4t
.
12.6 Fourier Sine and Cosine Transforms
For semi-infinit e regions, the Fourier sine and cosine transforms determined
in Section 12.2 are particularly appropriate in solving boundary-value prob-
lems. Before we illustrate their applications, we must first prove the differ-
entiation theorem.
Theorem 12.6.1. Let f (x) and its first derivative vanish as x →∞.If
F
c
(k) is the Fourier cosine transform, then
F
c
[f
′′
(x)] = −k
2
F
c
(k) −
2
π
f
′
(0) . (12.6.1)
Proof.
F
c
[f
′′
(x)] =
2
π
∞
0
f
′′
(x)coskx dx

12.6 Fourier Sine and Cosine Transforms 457
=
2
π
[f
′
(x)coskx]
∞
0
+
2
π
k
∞
0
f
′
(x)sinkx dx
= −
2
π
f
′
(0) +
2
π
k [f (x)sinkx]
∞
0
−
2
π
k
2
∞
0
f (x)coskx dx
= −
2
π
f
′
(0) − k
2
F
c
(k) .
In a similar manner, the Fourier cosine transforms of higher-order
derivatives of f (x) can be obtained.
Theorem 12.6.2. Let f (x) and its first derivative vanish as x →∞.If
F
s
(k) is the Fourier sine transform, then
F
s
[f
′′
(x)] =
2
π
kf(0) − k
2
F
s
(k) . (12.6.2)
The proof is left to th e reader.
Example 12.6.2. Find the temperature distribution in a semi-infinite rod
for the followin g cases with zero initial temperature distribution:
(a) The heat supplied at the end x = 0 at the rate g (t);
(b) The end x = 0 is kept at a constant temperature T
0
.
The problem here is to solve the heat conduction equation
u
t
= κu
xx
,x>0,t>0,
u (x , 0) = 0,x>0.
(a) u
x
(0,t)=g (t) and (b) u (0,t)=T
0
,t≥ 0. Here we assume th at u (x, t)
and u
x
(x, t) vanish as x →∞.
For case (a), let U (k, t) be the Fourier cosine transform of u (x, t).
Then the transformation of the heat conduction equation yields
U
t
+ κk
2
U = −
2
π
g (t) κ.
The solution of this equation with U (k, 0) = 0 is
u (x , t)=
2
π
∞
0
U (k, t)coskx dk
= −
2κ
π
t
0
g (τ) dτ
∞
0
e
−κk
2
(t−τ)
cos kx dk.

458 12 Integral Transform Methods with Applications
The inner integral is given by (see Problem 6, Exercises 12.18)
∞
0
e
−k
2
κ(t−τ)
cos kx dk =
1
2
π
κ (t − τ)
exp
−
x
2
4κ (t − τ)
.
The solution, therefore, is
u (x , t)=−
κ
π
t
0
g (τ)
√
t − τ
e
−x
2
/4κ(t−τ)
dτ. (12.6.3)
For case (b), we app ly the Fourier sine transform U (k, t)ofu (x, t)to
obtain the transformed equation
U
t
+ κk
2
U =
2
π
kT
0
κ.
The solution of this equation with zero in itial condition is
U (k, t)=T
0
2
π
1 − e
−κtk
2
k
.
Then the inverse Fourier sine transformation gives
u (x , t)=
2T
0
π
∞
0
sin kx
k
1 − e
−κtk
2
dk.
Making use of the integral
∞
0
e
−a
2
x
2
sin kx
k
dk =
π
2
erf
x
2a
,
the solution is found to b e
u (x , t)=
2T
0
π
π
2
−
π
2
erf
x
2
√
κt
= T
0
erfc
x
2
√
κt
, (12.6.4)
where erfc (x)=1−erf (x) is the complementary error function defined by
erfc (x)=
2
√
π
∞
x
e
−α
2
dα.
12.7 Asymptotic Approximation of Integrals by
Stationary Phase Method
Although definite integrals represent exact solutions for many physical
problems, the physical meaning of the solutions is often difficult to de-
termine. In many cases the exact evaluation of the integrals is a formidable
task. It is then necessary to resort to asymptotic methods.
12.7 Asymptotic Approximation o f Integrals by Stationary Phase Method 459
We consider the typical integral solution
u (x , t)=
b
a
F (k) e
itθ(k)
dk, (12.7.1)
where F (k) is called the spectral function determined by the initial or
boundary data in a<k<b,andθ (k), known as the phase function, is
given by
θ (k) ≡ k
x
t
− ω (k) ,x>0. (12.7.2)
We examine the asymptotic behavior of (12.7.1) for both large x and
large t; one of the interesting limits is t →∞with (x/t) held fixed. Integral
(12.7.1) can be evaluated by the Kelvin stationary phase method for large
t.Ast →∞, the integrand of (12.7.1) oscillates very rapidly; consequently,
the contributions to u (x, t) from adjacent parts of the integrand cancel one
another except in the neighborhood of the points, if any, at which the phase
function θ (k) is stationary, that is, θ
′
(k) = 0. Thus, the main contribution
to the integral for large t comes from the neighb orh ood of the point k = k
1
which determined by the solution of
θ
′
(k
1
)=
x
t
− ω
′
(k
1
)=0,a<k
1
<b. (12.7.3)
The point k = k
1
known as the point of stationary phase,orsimply,sta-
tionary point.
We expand both F (k)andθ (k) in Taylor series about k = k
1
so that
u (x , t)=
b
a
F (k
1
)+(k − k
1
) F
′
(k
1
)+
1
2
(k − k
1
)
2
F
′′
(k
1
)+...
×exp
it
θ (k
1
)+
1
2
(k − k
1
)
2
θ
′′
(k
1
)
+
1
6
(k − k
1
)
3
θ
′′′
(k
1
)+...
dk (12.7.4)
provided that θ
′′
(k
1
) =0.
Introducing the change of variable k − k
1
= εα,where
ε (t)=
2
t |θ
′′
(k
1
)|
1
2
, (12.7.5)
we find that the significant contribution to integral (12.7.4) is
u (x , t) ∼ ε
(b−k
1
)/ε
−(k
1
−a)/ε
F (k
1
)+εαF
′
(k
1
)+
1
2
ε
2
α
2
F
′′
(k
1
)+...
×exp
i
tθ(k
1
)+α
2
sgn θ
′′
(k
1
)+
1
3
ε
θ
′′′
(k
1
)
|θ
′′
(k
1
)|
α
3
+ ...
dα,
(12.7.6)

460 12 Integral Transform Methods with Applications
where sgn x denotes the signum function defined by sgn x =1,x>0and
sgn x = −1, x<0.
We then proceed to the limit as ε → 0(t →∞) and use the standard
integral
∞
−∞
exp
±iα
2
dα =
√
π exp
±
iπ
4
(12.7.7)
to obtain the asymptotic approximation as t →∞,
u (x , t) ∼ F (k
1
)
2π
t |θ
′′
(k
1
)|
1
2
exp
(
i
"
tθ(k
1
)+
π
4
sgn θ
′′
(k
1
)
#)
+ O
ε
2
,
(12.7.8)
where O
ε
2
means that a function tends to zero like ε
2
(t)ast →∞.If
there is more than one stationary point, each one contributes a term similar
to (12.7.8) and we obtain, for n stationary points k = k
r
,r=1, 2,...n;
u(x, t) ∼
n
r=1
F (k
r
)
2π
t |θ
′′
(k
r
)|
1
2
exp
(
i
"
tθ(k
r
)+
π
4
sgn θ
′′
(k
r
)
#)
,t→∞.
(12.7.9)
If θ
′′
(k
1
) = 0, but θ
′′′
(k
1
) = 0, then asymptotic approximation (12.7.8)
fails. This impor tant special case can be handled in a similar fashion. The
asymptotic approximation of (12.7.1) is then given by
u (x , t)=F (k
1
)exp{itθ (k
1
)}
∞
−∞
exp
i
6
tθ
′′′
(k
1
)(k − k
1
)
3
dk
∼ Γ
4
3
6
t |θ
′′′
(k
1
)|
1
3
F (k
1
)exp
itθ (k
1
)+
πi
6
+ O
t
−
2
3
as t →∞.
(12.7.10)
For an elaborate treatment of the stationary phase method, see Copson
(1965).
12.8 Laplace Transforms
Because of their simplicity, Laplace transforms are frequently used to solve
a wide class of partial differential equations. Like other transforms, Laplace
transforms are used to determine par ticular solutions. In solving partial
differential equations, the general solutions are difficult, if not impossible,
to obtain. The transform technique sometimes offers a useful tool for finding
particular solutions.
The Laplace transform is closely r elated to the complex Fourier trans-
form, so the Fourier integral formula (6.13.10) can be used to define
