Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

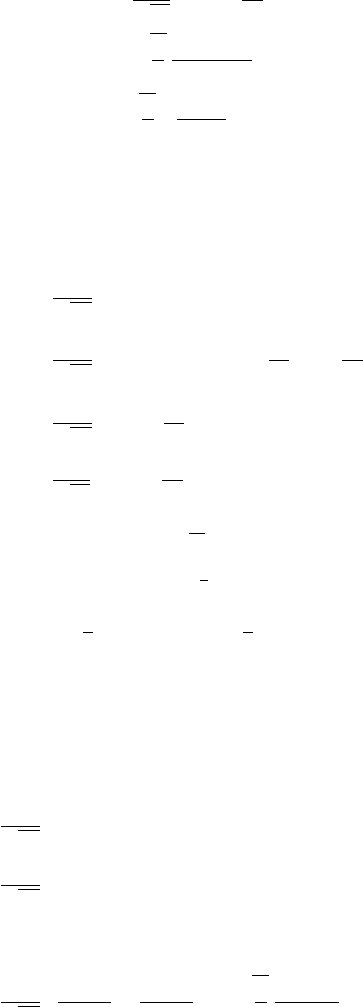
12.2 Fourier Transforms 441
Example 12.2.1. Show that
(a) F
&
exp
−ax
2
'
=
1
√
2a
exp
−
k
2
4a
,a>0, (12.2.3)
(b) F{exp (−a |x|)} =
2
π
a
(a
2
+ k
2
)
,a>0, (12.2.4)
(c) F
&
χ
[−a,a]
(x)
'
=
2
π
sin ak
k
, (12.2.5)
where χ
[−a,a]
(x)=H (a −|x|)=
⎧
⎨
⎩
1, |x| <a
0, |x| >a
⎫
⎬
⎭
. (12.2.6)
Proof. We have, by definition (12.2.1),
F
&
exp
−ax
2
'
=
1
√
2π
∞
−∞
e
−ikx−ax
2
dx
=
1
√
2π
∞
−∞
exp
−a
x +
ik
2a
2
−
k
2
4a
dx
=
1
√
2π
exp
−
k
2
4a
∞
−∞
e
−ay
2
dy
=
1
√
2a
exp
−
k
2
4a
,
in which the change of variable y =
x +
ik
2a
is used. The above result is
correct, and the change of variable can be justified by methods of complex
analysis because (ik/2a) is complex. If a =
1
2
,then
F
exp
−
1
2
x
2
=exp
−
1
2
k
2
. (12.2.7)
This shows that F{f (x)} = f (k). Such a function is said to be self-
reciprocal under the Fourier transformation.
The graphs of f (x)=e
−ax
2
and F (k)=F{f (x)} are shown in Figure
12.2.1 for a =1.
To prove (b), we write
F{exp (−a |x|)} =
1
√
2π
∞
−∞
exp (−a |x|−ikx) dx
=
1
√
2π
0
−∞
exp {(a − ik) x}dx
+
∞
0
exp {−(a + ik ) x}dx
=
1
√
2π
1
a − ik
+
1
a + ik
=
2
π
a
a
2
+ k
2
.
442 12 Integral Transform Methods with Applications
Figure 12.2.1 Graphs of f (x) = exp(−ax
2
) and F (k).
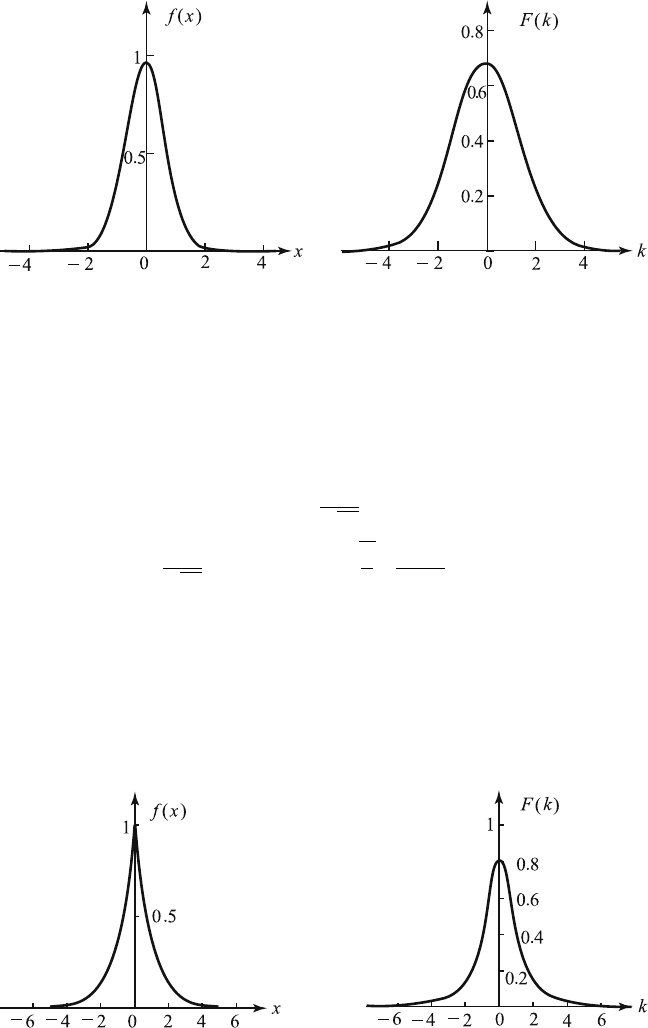
It is noted that f (x)=exp(−a |x|) decreases rapidly at infinity, and it is
not differentiable at x = 0. The graphs of f (x) an d its Fourier transform
F (k) are shown in Figure 12.2.2.
Toprove(c),wehave
F
a
(k)=F
&
χ
[−a,a]
(x)
'
=
1
√
2π
∞
−∞
e
−ikx
χ
[−a,a]
(x) dx
=
1
√
2π
a
−a
e
−ikx
dx =
2
π
sin ak
a
.
The graphs of χ
[−a,a]
(x)andF
a
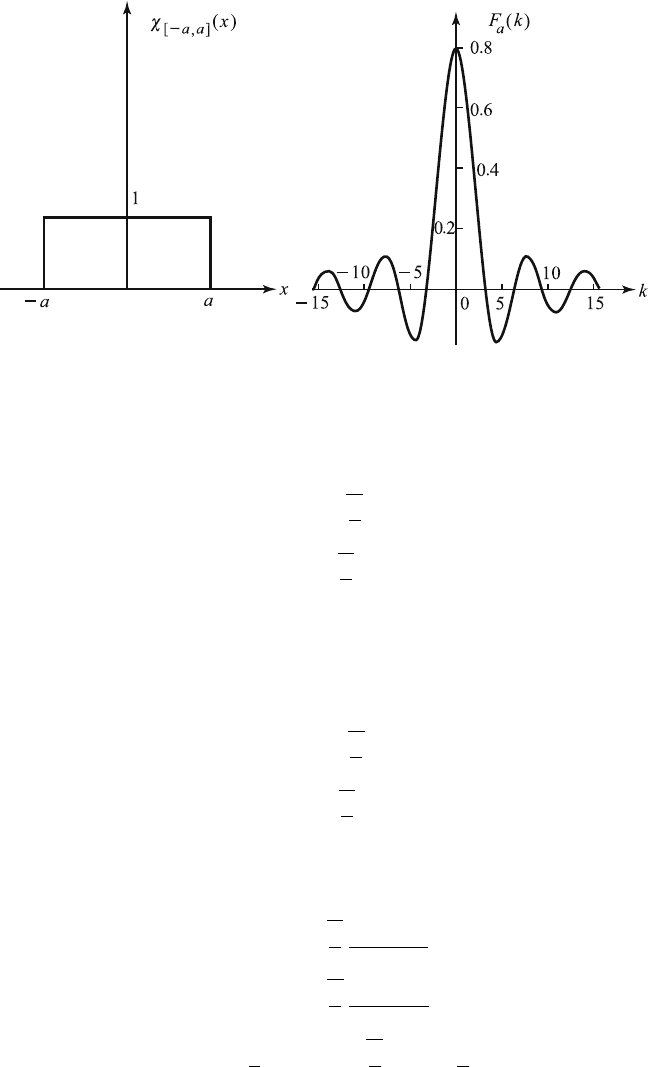
(k) are shown in Figure 12.2.3 with a =1.
Analogous to the Fourier cosine and sine series, there are Fourier cosine
and sine int egral transforms for odd and even functions respectively.
Definition 12.2.2. Let f (x) be defined for 0 ≤ x<∞, and extended
as an even function in (−∞, ∞) satisfying the conditions of Fourier Inte-
Figure 12.2.2 Graphs of f (x)=exp(−a |x|) and F (k).
12.2 Fourier Transforms 443
Figure 12.2.3 Graphs of χ
[−a,a]
(x) and F
a
(k).
gral formula (6.13.9). Then, at the points of continuity, the Fourier cosine
transform of f (x) and its inverse transform are defined by
F
c
{f (x)} = F
c
(k)=
2
π
∞
0
cos kx f (x) dx, (12.2.8)
F
−1
c
{F
c
(k)} = f (x)=
2
π
∞
0
cos kx F
c
(k) dk, (12.2.9)
where F
c
is the Fourier cosine transformation and F
−1
c
is its i nverse trans-
formation respectively.
Definition 12.2.3. Similarly, the Fourier sine integral formula (6.13.3)
leads to the Fourier sine transform and its inverse defined by
F
s
{f (x)} = F
s
(k)=
2
π
∞
0
sin kx f (x) dx, (12.2.10)
F
−1
s
{F
s
(k)} = f (x)=
2
π
∞
0
sin kx F
s
(k) dk, (12.2.11)
where F
s
is called the Fourier sine transformation and F
−1
s
is its inverse.
Example 12.2.2. Show that
(a) F
c
&
e
−ax
'
=
2
π
a
(a
2
+ k
2
)
,a>0, (12.2.12)
(b) F
s
&
e
−ax
'
=
2
π
k
(a
2
+ k
2
)
,a>0, (12.2.13)
(c) F
−1
s
1
k
e
−sk
=
2
π
tan
−1
x
s
. (12. 2.14)

444 12 Integral Transform Methods with Applications
We have, by definition,
F
c
&
e
−ax
'
=
2
π
∞
0
e
−ax
cos kx dk,
=
1
2
2
π
∞
0
"
e
−(a−ik)x
+ e
−(a+ik)x
#
dx,
=
1
2
2
π
1
a − ik
+
1
a + ik
=
2
π
a
(a
2
+ k
2
)
.
The proof of (b) is similar and is left to the reader as an exercise.
To prove (c), we use the standard definite integral
π
2
F
−1
s
&
e
−sk
'
=
∞
0
e
−sk
sin kx dk =
x
s
2
+ x
2
.
Integrating both sides with respect to s from s to ∞ gives
∞
0
e
−sk
k
sin kx dk =
∞
s
xds
x
2
+ s
2
=
"
tan
−1
s
x
#
=(π/2) − tan
−1
s
x
.
Consequently,
F
−1
s
1
k
e
−sk
=
2
π
∞
0
1
k
e
−sk
sin kx dk =
2
π
tan
−1
x
s
.
12.3 Properties of Fourier Transforms
Theorem 12.3.1. (Linearity). The Fourier transformation F is linear.
Proof.Wehave
F [f (x)] =
1
√
2π
∞
−∞
e
−ikx
f (x) dx.
Then, for any constants a and b,
F [af (x)+bg (x)] =
1
√
2π
∞
−∞
[af (x)+bg (x)] e
−ikx
dx,
=
a
√
2π
∞
−∞
f (x) e
−ikx
dx +
b
√
2π
∞
−∞
g (x) e
−ikx
dx,
= a F [f (x)] + b F [g (x)] .
Theorem 12.3.2. (Shifting). Let F [f (x)] be a Fourier transform of f (x).
Then
F [f (x − c)] = e
−ixc
F [f (x)] ,
where c is a real constant.
12.3 Properties of Fourier Transforms 445
Proof. From the definition, we have, for c>0,
F [f (x − c)] =
1
√
2π
∞
−∞
f (x − c) e
−ikx
dx,
=
1
√
2π
∞
−∞
f (ξ) e
−ik(ξ+c)
dξ, where ξ = x − c
= e
−ikc
F [f (x)] .
Theorem 12.3.3. (Scaling). If F is the Fourier transform of f,then
F [f (cx)]=(1/ |c|) F (k/c) ,
where c is a real nonzero constant.
Proof.Forc =0,
F [f (cx)] =
1
√
2π
∞
−∞
f (cx) e
−ikx
dx.
If we let ξ = cx,then
F [f (cx)] =
1
|c|
1
√
2π
∞
−∞
f (ξ) e
−i(k/c)ξ
dξ
=(1/ |c|) F (k/c) .
Theorem 12.3.4. (Differentiation). Let f be continuous and piecewise
smooth in (−∞, ∞). Let f (x) approach zero as |x|→∞.Iff and f
′
are absolutely integrable, then
F [f
′
(x)] = ikF [f (x)] = ikF (k) .
Proof.
F [f
′
(x)] =
1
√
2π
∞
−∞
f
′
(x) e
−ikx
dx,
=
1
√
2π
f (x) e
−ikx
∞
−∞
+
ik
√
2π
∞
−∞
f (x) e
−ikx
dx
,
= ikF [f (x)] = ikF (k) .
This result can be easily extended. If f and its first (n − 1) derivatives
are continuous, and if its nth derivative is piecewise continuous, then
F
"
f
(n)
(x)
#
=(ik)
n
F [f (x)]=(ik)
n
F (k) ,n=0, 1, 2,... (12.3.1)
provided f and its derivatives are absolutely integrable. In addition, we
assume that f and its first (n − 1) derivatives tend to zero as |x| tends to
infinity.
446 12 Integral Transform Methods with Applications
If u (x, t) → 0as|x|→∞,then
F
∂u
∂x
=
1
√
2π
∞
−∞
e
−ikx
∂u
∂x
dx,
which is, integrating by parts,
=
1
√
2π
e
−ikx
u (x , t)
!
∞
−∞
+
ik
√
2π
∞
−∞
e
−ikx
u (x , t) dx,
= ik F{u (x, t)} = ik U (k, t) . (12.3.2)
Similarly, if u (x, t) is continuously n times differentiable, and
∂
m
m
∂x
m
→ 0as
|x|→∞for m =1, 2, 3,...,(n − 1) then
F
∂
n
u
∂x
n
=(ik)
n
F{u (x, t)} =(ik)
n
U (k, t) . (12.3.3)
It also follows from the definition (12.2.1) that
F
∂u
∂t
=
dU
dt
, F
∂
2
u
∂t
2
=
d
2
U
dt
2
, ..., F
∂
n
u
∂t
n
=
d
n
U
dt
n
. (12.3.4)
The definition of the Fourier transform (12.2.1) shows that a sufficient con-
dition for u (x, t) to have a Four ier transform i s that u (x, t) is absolutely
integrable in −∞ <x<∞. This existence condition is too strong for many
practical applications. Many simple functions, such as a constant function,
sin ωx,andx
n
H (x), do not have Fourier transforms even though they occur
frequently in applications.
The above definition of the Fourier transform has been extended for a
more general class of f un ctions to include the above and other functions.
We simply state the fact that there is a sense, useful in practical applica-
tions, in which the above stated functions and many others do have Fourier
transforms. The following are examples of such functions and their Fourier
transforms (see Lighthill, 1964):
F{H (a −|x|)} =
2
π
sin ak
k
, (12.3.5)
where H (x) is the Heaviside unit step function,
F{δ (x − a)} =
1
√
2π
exp (−iak) , (12.3.6)
where δ (x − a) is the Dirac delta function, and
F{H (x − a)} =
π
2
1
iπk
+ δ (k)
exp (−iak) . (12.3.7)
12.3 Properties of Fourier Transforms 447
Example 12.3.1. Find the solution of the Dirichlet problem in the half-plane
y>0
u
xx
+ u
yy
=0, −∞ <x<∞,y>0,
u (x , 0) = f (x) , −∞ <x<∞,
u and u
x
vanish as |x|→∞, and u is bounded as y →∞.
Let U (k, y) be the Fourier transform of u (x, y) with respect to x.Then
U (k, y)=
1
√
2π
∞
−∞
u (x , y) e
−ikx
dx.
Application of the Fourier transform with respect to x gives
U
yy
− k
2
U =0, (12.3.8)
U (k, 0) = F (k)andU (k, y) → 0asy →∞. (12.3.9)
The solution of this transformed system is
U (k, y)=F (k) e
−|k|y
.
The inverse Fourier transform of U (k, y) gives the solution in the form
u (x , y)=
1
√
2π
∞
−∞
1
√
2π
∞
−∞
f (ξ) e
−|k|y
e
−ikξ
dξ
e
ikx
dk,
=
1
2π
∞
−∞
f (ξ) dξ
∞
−∞
e
−k[i(ξ−x)]−|k|y
dk.
It follows from the proof of Example 12.2.1 (b) that
∞
−∞
e
−k[i(ξ−x)]−|k|y
dk =
2y
(ξ − x)
2
+ y
2
.
Hence, the solution of the Dirichlet problem in the half-plane y>0is
u (x , y)=
y
π
∞
−∞
f (ξ)
(ξ − x)
2
+ y
2
dξ.
From this solution, we can readily deduce a solution of the Neumann
problem in the half-plane y>0.
Example 12.3.2. Find the solution of Neumann’s problem in the half -plane
y>0
u
xx
+ u
yy
=0, −∞ <x<∞,y>0,
u
y
(x, 0) = g (x) , −∞ <x<∞,
u is bounded as y →∞,uand u
x
vanish as |x|→∞.
448 12 Integral Transform Methods with Applications
Let v (x, y)=u
y
(x, y). Then
u (x , y)=
y
v (x, η) dη
and the Neumann problem becomes
∂
2
v
∂x
2
+
∂
2
v
∂y
2
=
∂
2
u
y
∂x
2
+
∂
2
u
y
∂y
2
=
∂
∂y
(u
xx
+ u
yy
)=0.
v (x, 0) = u
y
(x, 0) = g (x) .
This is the Dirichlet prob lem for v (x, y), and its solution is given by
v (x, y)=
y
π
∞
−∞
g (ξ) dξ
(ξ − x)
2
+ y
2
.
Thus, we have
u (x , y)=
1
π
y
η
∞
−∞
g (ξ) dξ
(ξ − x)
2
+ η
2
dη,
=
1
2π
∞
−∞
g (ξ) dξ
y
2ηdη
(ξ − x)
2
+ η
2
,
=
1
2π
∞
−∞
g (ξ)log
"
(x − ξ)
2
+ y
2
#
dξ,
where an arbitrary constant can be added to this solution. In other words,
the solution of any Neumann’s problem is uniquely determined up to an
arbitrary constant.
12.4 Convolution Theorem of the Fourier Transform
The function
(f ∗g)(x)=
1
√
2π
∞
−∞
f (x − ξ) g (ξ) dξ (12.4.1)
is called the convolution of the functions f and g over the interval (−∞, ∞).
Theorem 12.4.1. (Convolution Theorem). If F (k)andG (k) are the
Fourier transforms of f (x)andg (x) respectively, then the Fourier trans-
form of the convolution (f ∗ g) is the product F (k) G (k). That is,
F{f (x) ∗ g (x)} = F (k) G (k) . (12.4.2)
Or, equivalently,

12.4 Convolution Theorem of the Fourier Transform 449
F
−1
{F (k) G (k)} = f (x) ∗ g (x) . (12.4.3)
More explicitly,
1
√
2π
∞
−∞
F (k) G (k) e
ikx
dk =(f ∗ g)(x)
=
1
√
2π
∞
−∞
f (x − ξ) g (ξ) dξ. (12.4.4)
Proof.Bydefinition,wehave
F [(f ∗g)(x)] =
1
2π
∞
−∞
e
−ikx
dx
∞
−∞
f (x − ξ) g (ξ) dξ,
=
1
2π
∞
−∞
g (ξ) e
−ikξ
dξ
∞
−∞
f (x − ξ) e
−ik(x−ξ)
dx.
With the change of variable η = x − ξ,wehave
F [(f ∗g)(x)] =
1
√
2π
∞
−∞
g (ξ) e
−ikξ
dξ
1
√
2π
∞
−∞
f (η) e
−ikη
dη
= F (k) G (k) .
The convolution satisfies the following properties:
1. f ∗ g = g ∗ f (commutative).
2. f ∗ (g ∗ h)=(f ∗ g) ∗ h (associative).
3. f ∗ (ag + bh)=a (f ∗g)+b (f ∗ h) , (distributive),
where a and b are constants.
Theorem 12.4.2. (Parseval’s formula).
∞
−∞
|f (x)|
2
dx =
∞
−∞
|F (k)|
2
dk. (12.4.5)
Proof. The convolution formula (12.4.4) gives
∞
−∞
f (x) g (ξ − x) dx =
∞
−∞
F (k) G (k) e
ikξ
dk
which is, by putting ξ =0,
∞
−∞
f (x) g (−x) dx =
∞
−∞
F (k) G (k) dk. (12.4.6)
Putting g (−x)=
f (x),
G (k)=
1
√
2π
∞
−∞
g (x) e
−ikx
dx =
1
√
2π
∞
−∞
f (−x) e
−ikx
dx,
=
1
√
2π
∞
−∞
f (x) e
−ikx
dx =
F (k) ,

450 12 Integral Transform Methods with Applications
where the bar denotes the complex conjugate.
Thus, result (12.4.6) becomes
∞
−∞
f (x)
f (x) dx =
∞
−∞
F (k)
F (k) dk,
or,
∞
−∞
|f (x)|
2
dx =
∞
−∞
|F (k)|
2
dk.
In terms of the notation of the n orm, this is
f = F .
For physical systems, the quantity |f|
2
is a measure of energy, and |F |
2
represents the power spectrum of f (x).
Example 12.4.3. Obtain the solution of the initial-value problem of heat
conduction in an infinite rod
u
t
= κu
xx
, −∞ <x<∞,t>0, (12.4.7)
u (x , 0) = f (x) , −∞ <x<∞, (12.4.8)
u (x , t) → 0, as |x|→∞,
where u (x, t) represents the temperature distribution and is bounded, and
κ is a constant of diffusivity.
The Fourier transform of u (x, t) with respect to x is defined by
U (k, t)=
1
√
2π
∞
−∞
e
−ikx
u (x , t) dx.
In view of this transformation, equations (12.4.7)–(12.4.8) become
U
t
+ κk
2
U =0, (12.4.9)
U (k, 0) = F (k) . (12.4.10)
The solution of the transformed system is
U (k, t)=F (k) e
−k
2
κt
.
The inverse Fourier transformation gives the solution
u (x , t)=
1
√
2π
∞
−∞
F (k) e
−k
2
κt
e
ikx
dk
which is, by the convolution theorem 12.4.1,
