Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

11.2 The Dirac Delta Function 411

J =

∂ (u, v)

∂ (α, β)



=0. (11.2.9)

Consequently, we can write

δ (u − ξ) δ (v − η) |J| = δ (α − α

) δ (β − β

) . (11.2.10)

In particular, the transformation from rectangular Cartesian coordi-

nates (x, y) to polar coordinates (r, θ) is deﬁned by

x = r cos θ, y = r sin θ, (11.2.11)

so that the Jacobian J is

J =



= x

− y

= r. (11.2.12)

In this case, J vanishes at the origin and the transformation is singu lar

at r =0foranyθ. Hence, θ can be ign ored and

δ (x) δ (y)=

δ (r)

2π

δ (r)

, ( 11.2.13)

where



Jdθ=2πr.

Similarly, the transformation from three-dimensional rectangular Carte-

sian coordinates (x, y, z) to spherical polar coordinates (r, θ, φ)isgivenby

x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ, (11.2.14)

where 0 ≤ r<∞,0≤ θ ≤ π,and0≤ φ ≤ 2π.

The Jacobian of the transformation is

J = r

sin θ.

This Jacobian vanishes for all points on the z-axis, that is, for θ =0,and

hence, the coordinate φ may be ignored. Also, J vanishes at the origin

(r = 0) in which case both θ and φ may be ignored. Consequently,

δ (x) δ (y) δ (z)=

δ (r)

4πr

, (11.2.15)

where



2π

Jdθdφ=



2π

sin θdφ=4πr

412 11 Green’s Functions and Boundary-Value Problems

11.3 Properties of Green’s Functions

The solution of the Dirichlet problem in a domain D with boundary B

∇

u = h (x, y)inD

u = f (x, y)onB (11.3.1)

is given in Section 11.5 and has the form

u (x , y)=



G (x, y; ξ, η) h (ξ, η) dξ dη +



∂G

∂n

ds, (11.3.2)

where G is the Green’s function and n denotes the outward normal to the

boundary B of the region D. It is rather obvious then that the solution

u (x , y) can be determined as soon as the Green’s function G is ascertained,

so the problem in this technique is really to ﬁnd the Green’s function.

First, we shall deﬁne the Green’s function for the Dirichlet problem

involving the Laplace operator. Then, the Green’s function for the Dirichlet

problem involving th e Helmholtz operator may be deﬁned in a completely

analogous manner.

The Green’s function for the Dirichlet problem involving the Laplace

operator is the function which satisﬁes

(a)

∇

G = δ (x − ξ, y − η)inD, (11.3.3)

G =0 onB. (11.3.4)

(b) G is symmetric, that is,

G (x, y; ξ, η)=G (ξ,η; x, y) , (11.3.5)

point (ξ, η) which is speciﬁed by the equation

lim

ε→0



∂G

∂n

ds =1, (11.3.6)

where n is the outward normal to the circle

:(x − ξ)

+(y − η)

= ε

The Green’s function G may be interpreted as the response of the system

at a ﬁeld point (x, y) due to a δ function input at the source point (ξ,η).

G is continuous everywhere in D, and its ﬁrst and second derivatives are

continuous in D except at (ξ,η). Thus, property (a) essentially states that

∇

G = 0 everywhere except at the source point (ξ,η).

We will now prove property (b).

Theorem 11.3.1. The Green’s function is symmetric.

11.3 Properties of Green’s Functions 413

Proof. Applying the Green’s second formula





φ∇

ψ − ψ∇



dS =





∂ψ

∂n

− ψ

∂φ

∂n



ds, (11.3.7)

to the functions φ = G (x, y; ξ, η)andψ = G (x, y; ξ

∗

,η

∗

), we obtain



G (x, y; ξ, η) ∇

G (x, y; ξ

∗

,η

∗

) − G (x, y; ξ

∗

,η

∗

) ∇

G (x, y; ξ, η)

dx dy





G (x, y; ξ, η)

∂G

∂n

(x, y; ξ

∗

,η

∗

) − G (x, y; ξ

∗

,η

∗

)

∂G

∂n

(x, y; ξ, η)



ds.

Since G (x, y; ξ,η) and hence, G (x, y; ξ

∗

,η

∗

)mustvanishonB,wehave



G (x, y; ξ, η) ∇

G (x, y; ξ

∗

,η

∗

)

− G (x, y; ξ

∗

,η

∗

) ∇

G (x, y; ξ, η)

dx dy =0.

But

∇

G (x, y; ξ, η)=δ (x − ξ, y − η) ,

and

∇

G (x, y; ξ

∗

,η

∗

)=δ (x − ξ

∗

,y− η

∗

) .

Since



G (x, y; ξ, η) δ (x − ξ

∗

,y− η

∗

) dx dy = G (ξ

∗

,η

∗

; ξ, η) ,

and



G (x, y; ξ

∗

,η

∗

) δ (x − ξ,y − η) dx dy = G (ξ,η; ξ

∗

,η

∗

) ,

we obtain

G (ξ, η; ξ

∗

,η

∗

)=G (ξ

∗

,η

∗

; ξ, η) .

Theorem 11.3.2. ∂G/∂n is discontinuous at (ξ, η); in particular

lim

ε→0



∂G

∂n

ds =1,C

:(x − ξ)

+(y − η)

= ε

Proof.LetR

be the region bounded by C

. Then, integrating both sides

of equation (11.3.3), we obtain



∇

Gdx dy =



δ (x − ξ, y − η) dx dy =1.

414 11 Green’s Functions and Boundary-Value Problems

It therefore follows that

lim

ε→0



∇

Gdx dy =1. (11.3.8)

Thus, by the Divergence theorem of calculus,

lim

ε→0



∂G

∂n

ds =1.

11.4 Method of Green’s Functions

It is often convenient to seek G as the sum of a particular integral of the

nonhomogeneous equation and the solution of the associated homogeneous

equation. That is, G may assume the form

G (ξ, η; x, y)=F (ξ, η; x, y)+g (ξ, η; x, y) , (11.4.1)

where F , known as the free-space Green’s function, satisﬁes

∇

F = δ (ξ − x, η − y)inD, (11.4.2)

and g satisﬁes

∇

g =0 inD, (11.4.3)

so that by superposition G = F + g satisﬁes equation (11.3.3). Also G =0

on B requires that

g = −F on B. (11.4.4)

Note that F need not satisfy the boundary condition. Hereafter, (x, y) will

denote the source point.

Before we determine the solution of a particular problem, let us ﬁrst

ﬁnd F for the Laplace and Helmholtz operators.

(1) Laplace Operator

In this case, F must satisfy the equation

∇

F = δ (ξ − x, η − y)inD.

Then, for r =

(ξ − x)

+(η − y)

> 0, that is, for ξ = x, η = y,wehave

with (x, y) as the center

∇

F =

∂

∂r



∂F

∂r



=0,

11.4 Method of Green’s Functions 415

since F is independent of θ. Therefore, the solution is

F = A + B log r.

Applying condit ion (11.3.6), it follows directly from equation (11.3.8) with

∇

g =0,that

lim

ε→0



∂F

∂n

ds = lim

ε→0



2π

rdθ=1.

Thus, B =1/2π and A is arbitrary. For simplicity, we choose A =0.Then

F takes the form

F =

2π

log r. (11.4.5)

(2) Helmholtz Operator

Here F is required to satisfy

∇

F + κ

F = δ (x − ξ,y − η) .

Again for r>0, we ﬁnd

∂

∂r



∂F

∂r



+ κ

F =0,

or,

+ rF

+ κ

F =0.

This is the Bessel equation of order zero, the solution of which is

F (κr)=AJ

(κr)+BY

(κr) .

Since the behavior of J

at r = 0 is not singular, we set A =0.Thus,we

have

F (κr)=BY

(κr) .

But, for very small r,

(κr) ∼

log r.

Applying condition (11.3.6), we obtain

1 = lim

ε→0



∂F

∂n

ds = lim

ε→0



∂Y

∂r

ds = B ·

πr

· 2πr

and hence, B =1/4. Thus, F (κr) becomes

416 11 Green’s Functions and Boundary-Value Problems

F (κr)=

(κr) . (11.4.6)

We may point out that, since



∇

+ κ



approaches ∇

as κ → 0,

it should (and does) follow that

(κr) →

log r as κ → 0+.

11.5 Dirichlet’s Problem for the Laplace Operator

We are now in a position to determine the solution of th e Dirichlet problem

∇

u = h in D,

(11.5.1)

u = f on B,

by the method of Green’s function.

By putting φ (ξ, η)=G (ξ,η; x, y)andψ (ξ,η)=u (ξ, η) in equation

(11.3.7), we obtain



G (ξ, η; x, y) ∇

u − u (ξ,η) ∇

dξ dη





G (ξ, η; x, y)

∂u

∂n

− u (ξ, η)

∂G

∂n



ds.

But

∇

u = h (ξ, η)inD,

and

∇

G = δ (ξ − x, η − y)inD.

Thus, we have



[G (ξ, η; x, y) h (ξ, η) − u (ξ, η) δ (ξ − x, η − y)] dξ dη





G (ξ, η; x, y)

∂u

∂n

− u (ξ, η)

∂G

∂n



ds. (11.5.2)

Since G = 0 and u = f on B, and since G is symmetric, it follows that

u (x , y)=



G (x, y; ξ, η) h (ξ, η) dξ dη +



∂G

∂n

ds (11.5.3)

11.5 Dirichlet’s Problem for the Laplace Operator 417

which is the solution given by (11.3.2).

As a speciﬁc example, consider the Dirichlet problem for a unit circle.

Then

∇

g = g

ξξ

+ g

ηη

=0 inD,

(11.5.4)

g = −F on B.

But we already have from equation (11.4.5) that F =(1/2π)logr.

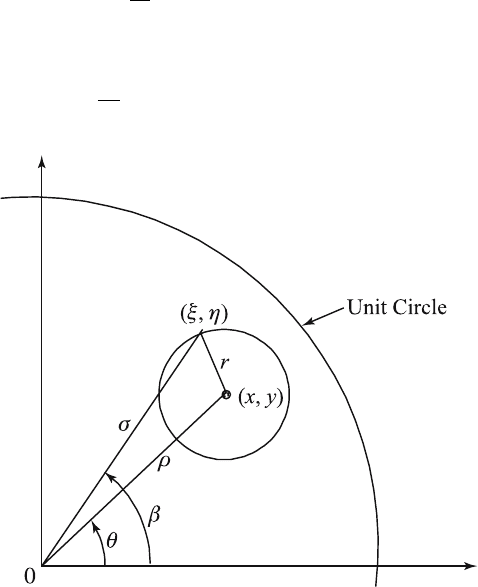
If we introduce the polar coordinates (see F igur e 11.5.1) ρ, θ, σ, β by

means of the equations

x = ρ cos θ, ξ = σ cos β,

(11.5.5)

y = ρ sin θ, η = σ sin β,

then the solution of equation (11.5.4) is [see Section 9.4]

g (σ, β)=

∞



n=1

cos nβ + b

sin nβ) ,

where

g = −

4π

log

1+ρ

− 2ρ cos (β − θ)

on B.

Figure 11.5.1 Image point.

418 11 Green’s Functions and Boundary-Value Problems

By using the relation

log

1+ρ

− 2ρ cos (β − θ)

= −2

∞



n=1

cos n (β − θ)

and equating the coeﬃcients of sin nβ and cos nβ to determine a

and b

we ﬁnd

2πn

cos nθ, b

2πn

sin nθ.

It therefore follows that

g (ρ, θ; σ, β)=

2π

∞



n=1

(σρ)

cos n (β − θ)

= −

4π

log

1+(σρ)

− 2(σρ) cos (β − θ)

Hence, the Green’s function for the problem is

G (ρ, θ; σ, β)=

4π

log

+ ρ

− 2σρ cos (β − θ)

−

4π

log

1+(σρ)

− 2σρ cos (β − θ)

, (11.5.6)

from which we ﬁnd

∂G

∂n



on B



∂G

∂σ



σ =1

2π

1 − ρ

[1 + ρ

− 2ρ cos (β − θ)]

If h = 0, then solution (11.5.3) reduces to the Poisson integral formula

similar to (9.4.10) and assumes the form

u (ρ, θ)=

2π



2π

1 − ρ

1+ρ

− 2ρ cos (β − θ)

f (β) dβ.

11.6 Dirichlet’s Problem for the Helmholtz Operator

We will n ow determine the Green’s function solution of the Dirichlet prob-

lem involving the Helmholtz operator, namely,

∇

u + κ

u = h in D,

(11.6.1)

u = f on B,

where D is a circular domain of unit radius with boundary B. Then, the

Green’s function mu st satisfy

11.6 Dirichlet’s Problem for the Helmholtz Operator 419

∇

G + κ

G = δ (ξ − x, η − y)inD,

(11.6.2)

G =0 onB.

Again, we seek the solution in the form

G (ξ, η; x, y)=F (ξ, η; x, y)+g (ξ, η; x, y) . (11.6.3)

From equation (11.4.6), we have

F =

(κr) , (11.6.4)

where r =

(ξ − x)

+(η − y)

. The function g must satisfy

∇

g + κ

g =0 inD,

(11.6.5)

g = −

(κr)onB.

This solution can be determined easily by the method of separation of

variables. Thus, th e solution in the polar coordinates deﬁned by equation

(11.5.5) may be written in the form

g (ρ, θ, σ, β)=

∞



n=0

(κσ)[a

cos nβ + b

sin nβ] , (11.6.6)

where

= −

8πJ

(κ)



−π



1+ρ

− 2ρ cos (β − θ)

dβ,

−

4πJ

(κ)

−π



1+ρ

− 2ρ cos (β − θ)

cos nβ dβ

−

4πJ

(κ)

−π



1+ρ

− 2ρ cos (β − θ)

sin nβ dβ

⎫

⎪

⎬

⎪

⎭

n =1, 2,....

To ﬁnd the solution of the Dirichlet problem, we multiply both sides of

the ﬁrst equation of equation (11.6.1) by G and integrate. Thus, we have





∇

u + κ



G (ξ, η; x, y) dξ dη =



h (ξ, η) G (ξ, η; x, y) dξ dη.

We then apply Green’s theorem on the left side of the preceding equation

and obtain



h (ξ, η) G (ξ, η; x, y) dξ dη −





∇

G + κ



dξ dη



(Gu

− uG

) ds.

420 11 Green’s Functions and Boundary-Value Problems

But ∇

G + κ

G = δ (ξ − x, η − y)inD and G =0onB. We, therefore,

have

u (x , y)=



h (ξ, η) G (ξ, η; x, y) dξ dη +



f (ξ, η) G

ds, (11.6.7)

where G is given by equation (11.6.3) with equations (11.6.4) and (11.6.6).

11.7 Method of Images

We shall describe another method of obtaining Green’s functions. This

method, called the method of images, i s based essentially on the construc-

tion of Green’s function for a ﬁnite domain from that of an inﬁnite domain.

The disadvantage of this method i s that it can be applied only to prob lems

with simple boundary geometry.

As an illustrati on, we consider the same Dirichlet problem solved in

Section 11.5.

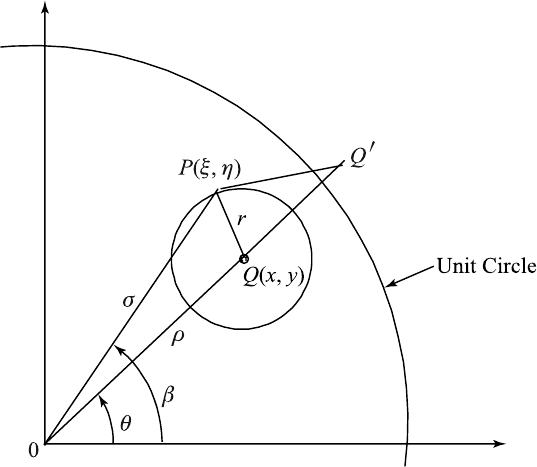
Let P (ξ,η)be a point in the unit circle D,andletQ (x, y) be the source

point also in D. The distance between P and Q is r.LetQ

′

be the image

which li es outside of D on the ray from the origin opposite to the source

point Q (as shown in Figure 11.7.1) such that OQ/σ = σ/OQ

′

,whereσ is

the radius of the circle passing through P centered at the origin.

Figure 11.7.1 Image point.