Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

10.9 Heat Conduction in a Rectangular Volume 381

10.9 Heat Conduction in a Rectangular Volume

As in the case of the wave equation, the solution of the heat equation in

three spaces variables can be determined. Consider the problem of heat

distribution in a rectangular volume. The faces are maintained at zero de-

gree temperature. The solid is initially heated so that the problem may be

written as

= k ∇

u, 0 <x<a, 0 <y<b, 0 <z<d, t>0,

u (x , y, z, 0) = f (x, y, z) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ d,

u (0,y,z,t)=0,u(a, y, z, t)=0,

u (x , 0,z,t)=0,u(x, b, z, t)=0,

u (x , y, 0,t)=0,u(x, y, d, t)=0.

As before, the separable equations are

′

+ λkT =0, (10.9.1)

∇

U + λU =0. (10.9.2)

If we assume the solution U to be of the form

U (x, y, z)=X (x) Y (y) Z (z) ,

then the solution of the Helmholtz equation is

lmn

(x, y, z)=B

sin



lπx



sin



mπy



sin



nπz



Since the solution of equation (10.9.1) is

T (t)=Ge

−λkt

the solution of the heat equation takes the form

u (x , y, z, t)=

∞



l=1

∞



m=1

∞



n=1

lmn

−λkt

sin



lπx



sin



mπy



sin



nπz



where λ =











!

and a

lmn

are constants.

Application of the initial condition yields

lmn



abd





f (x, y, z)sin



lπx



sin



mπy



sin



nπz



dx dy dz.

382 10 Higher-Dimensional Boundary-Value Problems

10.10 The Schr¨odinger Equation and the Hydrogen

Atom

In quantum mechanics, the Hamiltonian (or energy operator) is usually

denoted by H andisdeﬁnedby

H =

+ V (r) (10.10.1)

where p =(/i) ∇ = −i∇ is the momentum of a particle of mass M,

h =2π is the Planck constant, and V (r) is the potential energy.

The physical state of a particle at time t is described as fully as possible

by the wave function Ψ (r,t). The probability of ﬁnding the particle at

position r =(x, y, z) within a ﬁnite volume dV = dx dy dz is



|Ψ|

dx dy dz.

The particle must always b e somewhere in the space, so the probab ility of

ﬁnding the particle within the whole space is one, that is,



∞

−∞



∞

−∞



∞

−∞

|Ψ|

dx dy dz =1.

The time d ependent Schr¨odinger equation for the function Ψ (r,t)is

i Ψ

= HΨ, (10.10.2)

where H is explicitly given by

H = −



∇

+ V (r) . (10.10.3)

Given the potential V (r), the fundamental problem of quantum me-

chanics is to obtain a solution of (10.10.2) which agrees with a given initial

state Ψ (r, 0).

For the stationary state solutions, we seek a solution of the form

Ψ (r,t)=f (t) ψ (r) .

Substituting this into (10.10.2) gives



f =0, (10.10.4)

Hψ(r)=Eψ (r) , (10.10.5)

where E is a separation constant and has the dimension of energy. Integra-

tion of (10.10.4) gives

10.10 The Schr¨odinger Equation and the Hydrogen Atom 383

f (t)=A exp



−

iEt





, (10.10.6)

where A is an arbitrary constant.

Equation (10.10.5) is called the time independent Schr¨odinger equation.

The great importance of this equation follows from the fact that the sepa-

ration of variables gives not just some particular solution of (10.10.5), but

generally yields all solutions of physical interest. If ψ

(r) represents one

particular solution of (10.10.5), then most general solutions of (10.10.2) can

be obtained by the principle of superposition of such particular solutions.

In fact, the general solution is given by

ψ (r,t)=



exp



−

iEt





(r) , (10.10.7)

where the summation is taken over all admissible values of E,andA

an arbitrary constant to be determined from the initial conditions.

We now solve the eigenvalue pr oblem for the Schr¨odinger equation for

the spherically symmetric potential so that V (r)=V (r). The equation for

the wave function ψ (r)is

∇

ψ +



[E − V (r)] ψ =0, (10.10.8)

where ∇

is the three-dimensional Laplacian.

To determine the wave function ψ, it is convenient to introduce spherical

polar coordinates (r, θ, φ) so that equation (10.10.8) takes the form

∂

∂r



∂ψ

∂r



sin θ

∂

∂θ



sin θ

∂ψ

∂θ



sin

∂

∂φ

+K [E − V (r)] ψ =0, (10.10.9)

where K =



2M/



, ψ ≡ ψ (r, θ, φ), 0 ≤ r<∞,0≤ θ ≤ π,and0≤ φ ≤

2π.

We seek a nontrivial separable solution of the f orm

ψ = R (r) Y (θ, φ)

and then substitute into (10.10.9) to obtain the following equations





K (E − V ) r

− λ

R =0, (10.10.10)



sin θ

∂

∂θ



sin θ

∂

∂θ



sin

∂

∂φ



Y + λY =0, (10.10.11)

where λ is a separation constant.

384 10 Higher-Dimensional Boundary-Value Problems

We ﬁrst solve (10.10.11) by separation of variables through Y =

Θ (θ) Φ (φ) so that the equation becomes

sin θ

dθ



sin θ

dΘ

dθ





λ sin

θ − m



Θ =0, (10.10.12)

dφ

+ m

Φ =0, (10.10.13)

where m

is a separation constant.

The general solution of (10.10.13) is

Φ = Ae

imφ

+ Be

−imφ

where A and B are arbitrary constants to be determined by the boundary

conditions on ψ (r, θ, φ)=R (r) Θ (θ) Φ (φ) which will now be formulated.

According to the fundamental postulate of quantum mechanics, the

wave function for a particle without spin must have a deﬁnite value at

every point in space. Hence, we assume that ψ is a single-valued fu nction

of position. In particular, ψ must have the same value whether the az-

imuthal coordinate φ is given by φ or φ +2π,thatis,Φ (φ)=Φ (φ +2π).

Consequently, the solution for Φ has the form

Φ = Ce

imΦ

,m=0, +

1, + 2,..., (10.10.14)

where C is an arbitrary constant.

In order to solve (10.10.12), it is convenient to change the variable x =

cos θ , Θ (θ)=u (x), −1 ≤ x ≤ 1 so that this equation becomes





1 − x







λ −

1 − x



u =0. (10.10.15)

For the particular case m = 0, this equation becomes





1 − x





+ λu =0. (10.10.16)

This is known as the Legendre equation, which gives the Legendre poly-

nomials P

(x)ofdegreel as solutions provided λ = l (l +1) where l is a

positive integer or zero.

When m = 0, equation (10.10.15) with λ = l (l + 1) admits solutions

which are well known as associated Legendre functions, P

(x)ofdegreel

and order m deﬁned by

(x)=



1 − x



m/2

(x) ,x=cosθ.

Clearly, P

(x) vanishes when m>l. As for the negative integral values of

m, it can be readily shown that

10.10 The Schr¨odinger Equation and the Hydrogen Atom 385

−m

(x)=(−1)

(l − m)!

(l + m)!

(x) .

Hence, the functions P

−m

(x)diﬀerfromP

(x) by a constant factor, and

as a consequence, m is restricted to a positive integer or zero. Thus, the

associated Legendre functions P

(x)with|m|≤l are the only nonsingular

and physically acceptable solutions of (10.10.15). Since |m|≤l,whenl =0,

m =0;whenl =1,m = −1, 0, +1; when l =2,m = −2, −1, 0, 1, 2,

etc. This means that, given l, there are exactly (2l + 1) diﬀerent values of

m = −l, ..., −1, 0, 1,..., l.Thenumbersl and m are called the orbital

quantum member and the magnetic quantum number respectively.

It is convenient to write down the solutions of (10.10.11) as functions

which are normalized with respect to an integration over the whole solid

angle. They are called spherical harmonics and are given by, for m ≥ 0,

(θ, φ)=



(2l +1)

4π

(l − m)!

(l + m)!



(−1)

imφ

(cos θ) . (10.10.17)

Spherical harmonics with negative m and with |m|≤l are deﬁned by

(θ, φ)=(−1)

−m

(θ, φ). (10.10.18)

We now return to a general discussion of the radial equation (10.10.10)

which becomes, under the transformation R (r)=P (r) /r,



K (E − V ) −



P (r)=0. (10.10.19)

Almost all cases of physical interest require V (r) to be ﬁnite everywhere

except at the origin r =0.Also,V (r) → 0asr →∞. The Coulomb and

square well potentials are typical examples of this kind. In the neighborhood

of r =0,V (r) can be neglected compared to the centrifugal term



∼ 1/r



so that equation (10.10.19) takes the form

−

l (l +1)

P (r) = 0 (10.10.20)

for all states with l = 0. The general solution of this equation is

P (r)=Ar

l+1

+ Br

−l

, (10.10.21)

where A and B are arbitrary constants. With the boundary condition

P (0) = 0, B = 0 so that the solution is proportional to r

l+1

On the other hand, in view of the assumption that V (r) → 0asr →∞,

the radial equation (10.10.19) reduces to

+ KE P (r)=0. (10.10.22)

386 10 Higher-Dimensional Boundary-Value Problems

The general solution of this equation is

P (r)=Ce

√

+ De

−ir

√

. (10.10.23)

The solution is oscillatory for E>0, and exponential in nature for E<0.

The oscillatory solutions are not physically acceptable because the wave

function does not tend to zero as r →∞.WhenE<0, the second term

in (10.10.23) tends to inﬁnity as r →∞. Consequently, the only physically

acceptable solutions for E>0, have the asymptotic form

P (r)=Ce

−αr/2

, (10.10.24)

where KE = −





Thus, the general solution of (10.10.19) can be written as

P (r)=f (r) e

−(α/2)r

so that f (r) satisﬁes the ordinar y diﬀerential equation

− α

−



KV +

l (l +1)



f =0. (10.10.25)

Note that this general solution is physically acceptable because the wave

function tends to zero as r → 0andasr →∞.

We now specify the form of the potential V (r). One of the most com-

mon potentials is the Coulomb potential V (r)=−Ze

/r representing the

attraction between an atomic nucleus of charge +Ze and a moving electron

of charge −e. For the hydrogen atom Z = 1. It is a two particle system con-

sisting of a negatively charged electron interacting with a positively charged

proton. On the other hand, a helium atom consists of two protons and two

neutrons. There are two electrons in orbit around the nucleus of a helium

atom. For the singly charged helium ion Z =2,whereZ represents the

number of unit charges of the nucleus. Consequently, equation (10.10.25)

reduces to

− α



KZe

−

l (l +1)



f (r)=0. (10.10.26)

We seek a power series solution of this equation in the form

f (r)=r

∞



s=1

,k=0. (10.10.27)

Substituting this series into (10.10.26), we obtain

∞



s=1

[(s + k)(s + k − 1) − l (l + 1)] a

s+k−1

∞



s=1

Zke

− α (s + k)

s+k−1

=0.

10.10 The Schr¨odinger Equation and the Hydrogen Atom 387

Clearly, the lowest power of r is (k − 1), so that

[k (k +1)− l (l + 1)] a

=0.

This implies that k = l or −(l + 1) provided a

= 0. The negative ro ot of k

is not acceptable because it leads to an unbounded solution. Equating the

coeﬃcient of r

s+k−1

, we get the recurrence relation for the coeﬃcients as

s+1

α (s + l) − ZKe

s (s +2l +1)

,s=1, 2, 3,.... (10.10.28)

The asymptotic nature of this result is

s+1

∼

as s →∞.

This ratio is the same as that of the series for e

αr

. This means that R (r)is

unbounded as r →∞, which is p hysically unacceptable. Hence, the series

for f (r) must terminate, and f (r) must be a polynomial so that a

s+1

=0,

but a

= 0. Hence

α (s + l) − ZKe

=0,s=1, 2, 3,...,

or,

4(s + l)

= −KE. (10.10.29)

Putting K =



2M/



, the energy levels ar e given by

E = E

= −

2

, (10.10.30)

where n =(s + l) is called the pri ncipal quantum number and n =1, 2, 3,....

Thus, it tu rn s out that the complete solution of the Schr¨odinger equation

is given by

n,l,m

(r, θ, φ)=R

n,l

(r) Y

(θ, φ) ,

where the radial part is the solution of the radial equation (10.10.10), and

it depends on the principle quantum number n (energy levels) and the

orbital quantum number l. However, it does not depend on the magnetic

quantum number m. Of course, there are (2l + 1) states with the same l

value but with diﬀerent m values. Each of these states has the same energy,

and therefore, such systems have a (2l + 1)-fold degeneracy, as a result of

rotational symmetry.

For the hydrogen atom, Z = 1, the discrete energy spectrum is

= −

2

= −

2an

, (10.10.31)

388 10 Higher-Dimensional Boundary-Value Problems

where a =







is called the Bohr radius of the hydrogen atom of

mass M and charge of the electron, −e. This discrete energy spectrum

depends only on the principle quantum number n (but not on m) and has

an excellent agreement with experimental prediction of spectral lines.

For a given n, there are n sets of l and s

n =1, {l =0,s=1}; n =2,

⎧

⎨

⎩

l =0,s=2

l =1,s=1

⎫

⎬

⎭

;

n =3,

⎧

⎪

⎨

⎪

⎩

l =0,s=3

l =1,s=2

l =2,s=1

⎫

⎪

⎬

⎪

⎭

;etc.

Given n, there are exactly n values of l (l =0, 1, 2,...,n− 1) and the

highest value of l is n − 1.

Thus, the three numbers n, l, m, determine a unique eigenfunction,

n,l,m

(r, θ, φ)=R

n,l

(r) Y

(θ, φ). Since the energy levels depend only on

the pri nciple quantum number n, there are, in general, several linearly inde-

pendent eigenfunctions of the Schr¨odinger equation for the hydrogen atom

corresponding to each energy level, so the energy levels are said to be de-

generate. There are (2l + 1) diﬀerent eigenfunctions of the same energy

obtained by varying the magnetic quantum number m from −l to l.In

general, the t otal number of degenerate energy states E

for the hydrogen

atom is then

n−1



l=0

(2l +1)=2

n (n − 1)

+ n = n

. (10.10.32)

The energy levels of the hydrogen atom (10.10.31) can be expressed in

terms the Ry dberg, Ry ,as

= −

, (10.10.33)

where Ry represents the Rydberg given by

Ry =

2

2(c)



c



≃

5 × 10

eV ×



137



≃ 13.3 eV.

Consequently,

= −

13.3

eV. (10.10.34)

10.10 The Schr¨odinger Equation and the Hydrogen Atom 389

Thus, the ground state of the hydrogen atom, which is the most tightly

bound, has an energy −13.3 eV (more accurately −13.6 eV ) and therefore, it

would take 13.6 eV to release the electron from its ground state. Therefore,

this is called the binding energy of the hydrogen atom.

Finally, the electron is treated here as a nonrelativistic particle. How-

ever, in reality, small relativistic eﬀects can be calculated. These are known

as ﬁne structure corrections. Thus, the nonrelativistic Schr¨odinger equation

describes the hydrogen atom extremely well.

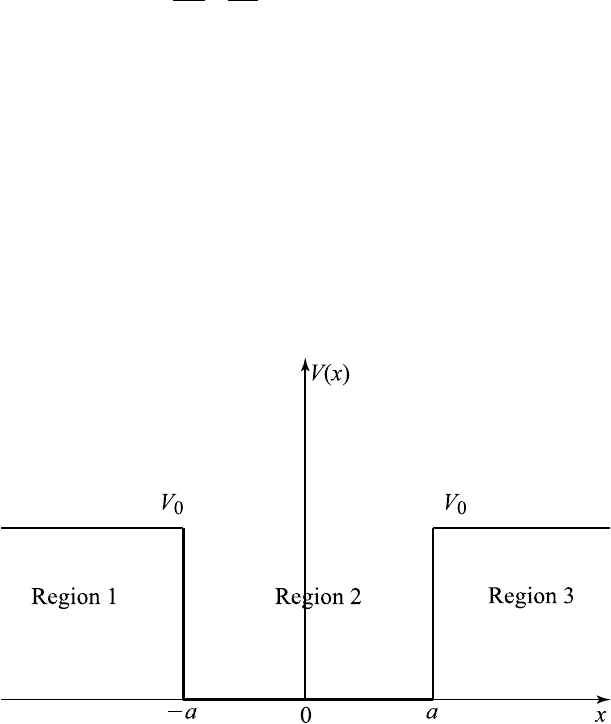
Example 10.10.1. (Inﬁnite Square well potential V

→∞). We consider

the one-dimensional Schr¨odinger equation (10.10.8) in the form



−







+ V (x)



ψ (x)=Eψ (x) , (10.10.35)

where the potential V (x)isgivenby

V (x)=

⎧

⎨

⎩

,x≤−a, x ≥ a,

0, −a ≤ x ≤ a

(10.10.36)

and take the li mit V

→ +∞ as shown in Figure 10.10.1.

It is noted that the potential is zero inside the square well and E is

the kinetic energy of the particle in this region (−a ≤ x ≤ a)whichmust

be positive, E>0. It is convenient to ﬁx the origin at the center of the

well so that V (x) is an even function of x. A case of special interest is that

>E≥ 0 and eventually, V

→∞.

Figure 10.10.1 Square well with potential V

→∞.

390 10 Higher-Dimensional Boundary-Value Problems

The given potential is diﬀerent in diﬀerent regions, we solve (10.10.35)

separately in three regions.

Region 1. V = V

in this region x ≤−a.

The Schr¨odinger equation (10.10.35) in this region is

−



+ V

ψ = Eψ.

Or, equivalently,







− E) ψ, V

>E>0. (10.10.37)

The general solution of (10.10.37) is

(x)=Ae

+ Be

−kx

, (10.10.38)

where A and B are constants and

k =





− E)



. (10.10.39)

The wave function ψ

(x) must be bounded as x →−∞to retain its prob-

abilistic interpretation, hence B = 0, and the solution in x ≤−a is

(x)=Ae

As V

→∞, k →∞, and, in this limit, the solution mu st vanish, that is,

(x)=0, for x ≤−a. (10.10.40)

Region 2. V =0in−a ≤ x ≤ a.

In this case, the equation takes the form

+ k

ψ =0, (10.10.41)

where

2ME



. (10.10.42)

The general solution of (10.10.41) is given by

(x)=C sin kx + D cos kx, (10.10.43)

where C and D are arbitrary constants.

Region 3. V = V

in this region x ≥ a.

An argument similar to region 1 leads to zero solution, that is,