Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

10.4 Dirichlet Problem for a Sphere 371

The coeﬃcients a

and b

are then found to be

= −

K +2

= E

(K − 1)

(K +2)

Hence, the potential for r ≤ a is given by

(r, θ)=−

K +2

r cos θ,

and the potential for r ≥ a is given by

(r, θ)=−E

r cos θ + E

(K − 1)

(K +2)

−2

cos θ.

Example 10.4.6. Determine the potential between concentric spheres held

at diﬀerent constant potentials.

Here we need to solve

∇

u =0, a<r<b,

u = A on r = a,

u = B on r = b.

In this case, the potential depends only on the radial distance. Hence, we

have

∂

∂r



∂u

∂r



=0.

By elementary integration, we obtain

u (r)=c

where c

and c

are arbitrary constants.

Applying the boundary conditions, we obtain

Bb − Aa

b − a

=(A − B)

b − a

Thus, the solution is

u (r)=

Bb − Aa

(b − a)

(A − B) ab

(b − a) r





r − a

b − a







b − r

b − a



372 10 Higher-Dimensional Boundary-Value Problems

10.5 Three-Dimensional Wave and Heat Equations

The wave equation in three space variables may be written as

= c

∇

u, (10.5.1)

where ∇

is the three-dimensional Laplace operator.

We assume a nontrivial separable solution in the form

u (x , y, z, t)=U (x, y, z) T (t) .

Substituting this into equation (10.5.1), we obtain

′′

+ λc

T =0, (10.5.2)

∇

U + λU =0, (10.5.3)

where −λ is a separation constant. The variables are separated and the

solutions of equations (10.5.2) and (10.5.3) are to be determined.

Next we consider the heat equation

= k∇

u. (10.5.4)

As before, we seek a nontrivial separable solution in the form

u (x , y, z, t)=U (x, y, z) T (t) .

Substituting this into equation (10.5.4), we obtain

′

+ λkT =0,

∇

U + λU =0.

Thus, we see that the problem here, as in the previous case, is essentially

that of solving the Helmholtz equation

∇

U + λU =0.

10.6 Vibrating Membrane

As a speciﬁc example of the higher-dimensional wave equation, let us de-

termine the solution of the problem of the vibratin g membrane of length

a and width b. The initial boundary-value problem for the displacement

function u (x, y, t)is

= c

+ u

) , 0 <x<a, 0 <y<b, t>0, (10.6.1)

u (x , y, 0) = f (x, y) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, (10.6.2)

(x, y, 0) = g (x, y) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, (10.6.3)

u (0,y,t)=0,u(a, y, t)=0, (10.6.4)

u (x , 0,t)=0,u(x, b, t)=0. ( 10.6.5)

10.6 Vibrating Membrane 373

We have just shown that the separated equations for the wave equation

are

′′

+ λc

T =0, (10.6.6)

∇

U + λU =0, (10.6.7)

where, in this case, ∇

U = U

+ U

.Letλ = α

. Then the solution of

equation (10.6.6) is

T (t)=A cos αct + B sin αct.

Now we look for a nontrivial solution of equation (10.6.7) in the form

U (x, y)=X (x) Y (y) .

Substituting this into equation (10.6.7) yields

′′

− µX =0,

′′

+(λ + µ) Y =0.

If we let µ = −β

, then the solutions of these equations take the form

X (x)=C cos βx + D sin βx.

Y (y)=E cos γy + F sin γy,

where

=(λ + µ)=α

− β

The homogeneous boundary conditions in x require that C = 0 and

D sin βa =0

which implies that β =(mπ/a)withD = 0. Similarly, the homogeneous

boundary conditions in y require that E = 0 and

F sin γb =0

which implies that γ =(nπ/b)withF = 0. Noting that m and n are

independent integers, we obtain the displacement function in the form

u (x , y, t)=

∞



m=1

∞



n=1

cos α

ct + b

sin α

ct)sin



mπx



sin



nπy



(10.6.8)

where α









, a

and b

are constants.

Now applying the nonhomogeneous initial conditions, we have

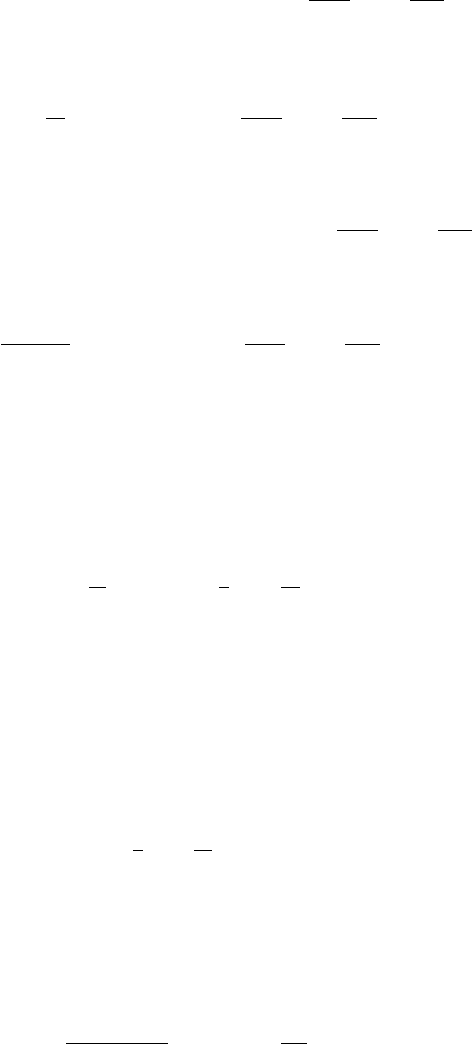
374 10 Higher-Dimensional Boundary-Value Problems

u (x , y, 0) = f (x, y)=

∞



m=1

∞



n=1

sin



mπx



sin



nπy



and thus,



f (x, y)sin



mπx



sin



nπy



dx dy. (10.6.9)

In a similar manner, the initial condition on u

implies

(x, y, 0) = g (x, y)=

∞



m=1

∞



n=1

c sin



mπx



sin



nπy



from which it follows that

abc



g (x, y)sin



mπx



sin



nπy



dx dy. (10.6.10)

The soluti on of the rectangular membrane problem is, therefore, given by

equation (10.6.8).

Example 10.6.1. (Vibration of a Circular Membrane). For a circular

elastic membrane that is stretched over a circular frame of radius a,the

motion of the membrane can be described by a function u (r, θ, t)that

satisﬁes the partial diﬀerential equation

= u

θθ

, (10.6.11)

where c

=(T/ρ), T is the tension in the membrane and ρ i s its mass

density.

We consider the synchronous vibrations of the vibration of the mem-

brane deﬁned by the separable solution

u (r, θ, t)=v (r, θ, t) cos (ωct) . (10.6.12)

Substituting (10.6.12) into (10.6.11) gives

θθ

+ ω

v =0. (10.6.13)

We seek a nontrivial separable solution

v (r, θ)=R (r) Θ (θ)

of equation (10.6.13) so that

′′

+ rR

′

+ ω

= −

′′

= λ

. (10.6.14)

10.7 Heat Flow in a Rectangular Plate 375

This must hold for all points of the membrane, 0 <r<aand 0 ≤ θ ≤ 2π.

Consequently,

′′

+ rR

′



− λ



R =0, 0 <r<a, (10.6.15)

′′

+ λ

Θ =0, 0 ≤ θ ≤ 2π. (10.6.16)

The general solution of (10.6.16) is

Θ (θ)=A cos λθ + B sin λθ. (10.6.17)

This represents a single-valued solution at all p oints of the disk only if

λ = n is an integer. Thus,

Θ (θ)=Θ

(θ)=A

cos nθ + B

sin nθ. (10.6.18)

With λ = n, the radial equation (10.6.15) becomes

′′

+ rR

′



− n



R =0. (10.6.19)

The parameter ω can be eliminated by deﬁning

x = ωr, and y (x)=y (ωr)=R (r) .

Substituting these into (10.6.19) gives

′′

+ xy

′



− n



y =0. (10.6.20)

Or, equivalently,

′′

′



1 −



y =0. (10.6.21)

This is the well-known Bessel equation of order n, which has been discussed

in Section 8.6.

10.7 Heat Flow in a Rectangular Plate

Another example of a two-dimensional problem is the conduction of heat

in a thin rectangular plate. Let the plate of length a and width b be per-

fectly insulated at the faces x = 0 and x = a. Let the two other sid es be

maintained at zero temperatu re. Let the initial temperature distribution be

f (x, y). Then, we seek the solution of the initial boundary-value problem

= k ∇

u, 0 <x<a, 0 <y<b, t>0, (10.7.1)

u (x , y, 0) = f (x, y) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, (10.7.2)

376 10 Higher-Dimensional Boundary-Value Problems

(0,y,t)=0,u

(a, y, t)=0, (10.7.3ab)

u (x , 0,t)=0,u(x, b, t)=0. (10.7.4ab)

As shown earlier, the separated equations for this problem are found to

′

+ λkT =0, (10.7.5)

∇

U + λU =0. (10.7.6)

We assume a nontrivial separable solution in the form

U (x, y)=X (x) Y (y) .

Inserting this in equation (10.7.6), we obtain

′′

− µX =0, (10.7.7)

′′

+(λ + µ) Y =0. (10.7.8)

Because the conditi ons in x are homogeneous, we choose µ = −α

so that

X (x)=A cos αx + B sin αx.

Since X

′

(0) = 0, B =0andsinceX

′

(a)=0,

sin αa =0,A=0

which gives

α =(mπ/a) ,m=1, 2, 3,....

We note that µ = 0 is also an eigenvalue. Consequently,

(x)=A

cos (mπx/a) ,m=0, 1, 2,....

Similarly, for nontrivial solution Y , we select β

= λ + µ = λ − α

so that

the solution of equation (10.7.8) is

Y (y)=C cos βy + D sin βy.

Applying the homogeneous conditions, we ﬁnd C = 0 and

sin βb =0,D=0.

Thus, we obtain

β =(nπ/b); n =1, 2, 3,...,

and

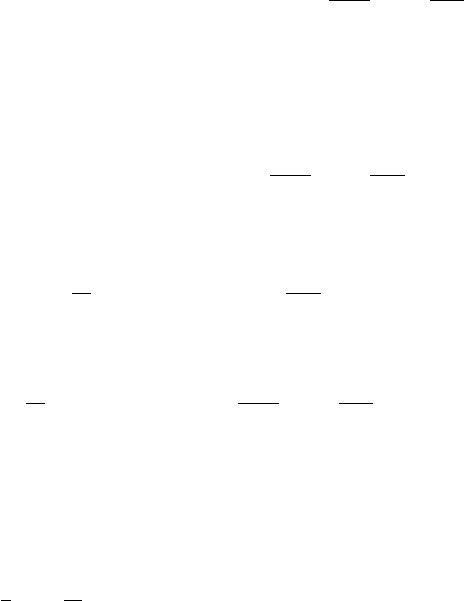
10.7 Heat Flow in a Rectangular Plate 377

(y)=D

sin (nπy/b) .

Recalling that λ = α

+ β

, the solution of equation (10.7.5) may be

writtenintheform

(t)=E

−

(

)

Thus, the solution of the heat equation satisfying the prescribed boundary

conditions may be written as

u (x , y, t)=

∞



m=0

∞



n=1

−

(

)

cos



mπx



sin



nπy



(10.7.9)

where a

= A

are arbitrary constants.

Applying the initial condition, we obtain

u (x , y, 0) = f (x, y)=

∞



m=0

∞



n=1

cos



mπx



sin



nπy



. (10.7.10)

This is a double Fourier series, and the coeﬃcients are given by







f (x, y)sin



nπy



dx dy,

and for m ≥ 1







f (x, y)cos



mπx



sin



nπy



dx dy.

The solution of the heat equation is thus given by equation (10.7.9).

Example 10.7.1. (Steady-state temperature in a Circular Disk). We

next consider the steady-state temperature distribution u (r, θ)inacircular

disk of radius r = a that satisﬁes the Laplace equation

θθ

=0, 0 ≤ r ≤ a, 0 ≤ θ ≤ 2π, (10.7.11)

u (r, θ)=f (θ) , on r = a for all θ, (10.7.12)

where f (θ) is a given function of θ.

This is exactly the Dirichlet problem for a circle that was already solved

in Section 9.4.

We also consider the steady-state temperature distribution u (r, θ, φ)

in a sphere of radius a where 0 ≤ r<a,0<θ<πand 0 <φ<

2π. For simplicity, we assume only steady temperature distribution which

depends on r and θ.Thus,u is independent of the longitudinal coordinate

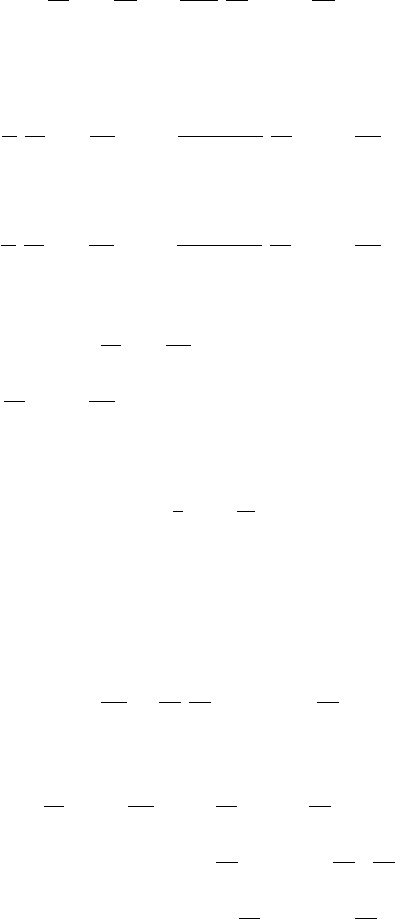
378 10 Higher-Dimensional Boundary-Value Problems

φ, and hence, the steady-state temperature distribution u (r, θ) satisﬁes the

Laplace equation in spherical polar coordinates in the form

∂

∂r



∂u

∂r



sin θ

∂

∂θ



sin θ

∂u

∂θ



=0. (10.7.13)

We seek a separable solution of (10.7.13) in the form u (r, θ)=R (r) Θ (θ)

so that (10.7.13) leads to





= −

Θ (θ)sinθ

dθ



sin θ

dΘ

dθ



=0. (10.7.14)

This must hold for 0 <r<aand 0 <θ<π. Consequently,





= −

Θ (θ)sinθ

dθ



sin θ

dΘ

dθ



= λ, (10.7.15)





− λR =0, 0 <r<a, (10.7.16)

dθ



sin θ

dΘ

dθ



+ λ sin θΘ(θ)=0, 0 <θ<π. (10.7.17)

Equation for R (r) can also be written as

′′

′

−

R =0. (10.7.18)

We simplify equation (10.7.17) by the change of variable.

x =cosθ, y (x)=Θ (θ) .

Using the chain rule we obtain

dΘ

dθ

= −(sin θ)

and hence,

dθ



sin θ

dΘ

dθ



= −

dθ



sin



= −





1 − x





dθ

=sinθ





1 − x





Combining this result with (10.7.17) leads to the Legendre equation

10.8 Waves in Three Dimensions 379





1 − x





+ λy =0, −1 ≤ x ≤ 1, (10.7.19)

or, equivalently,



1 − x



− 2x

+ λy =0. (10.7.20)

This equation was completely solved in Section 8.9. Equation (10.7.19) is

the well-known Sturm–Liouville equation with y (−1) and y (+1) ﬁnite. The

results are

λ = λ

= n (n +1),y(x)=P

(x) ,n=0, 1, 2, 3,...,

where P

(x) is the Legendre polynomial of degree n.

10.8 Waves in Three Dimensions

The propagation of waves due to an initial disturbance in a rectangular vol-

ume is best d escribed by the solution of the initial boundary-value problem

= c

∇

u, 0 <x<a, 0 <y<b, 0 <z<d, t>0,

(10.8.1)

u (x , y, z, 0) = f (x, y, z) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ d, (10.8.2)

(x, y, z, 0) = g (x, y, z) , 0 ≤ x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ d, (10.8.3)

u (0,y,z,t)=0,u(a, y, z, t)=0, (10.8.4)

u (x , 0,z,t)=0,u(x, b, z, t)=0, ( 10.8.5)

u (x , y, 0,t)=0,u(x, y, d, t)=0. (10.8.6)

We assume a nontrivial separable solution in the form

u (x , y, z, t)=U (x, y, z) T (t) .

The separated equations are given by

′′

+ λc

T =0, (10.8.7)

∇

U + λU =0. (10.8.8)

We assume that U has the n ontrivial separable solu tion in the form

U (x, y, z)=X (x) Y (y) Z (z) .

Substitution of this into equation (10.8.8) yields

′′

− µX =0, (10.8.9)

′′

− νY =0, (10.8.10)

′′

+(λ + µ + ν) Z =0. (10.8.11)

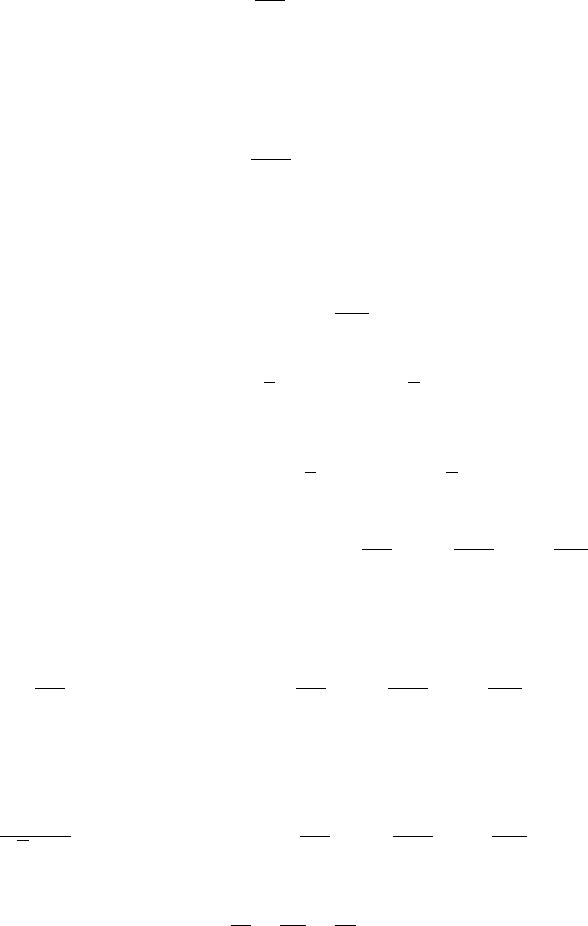
380 10 Higher-Dimensional Boundary-Value Problems

Because of the homogeneous conditions in x,weletµ = −α

so that

X (x)=A cos αx + B sin αx.

As in the preceding examples, we obtain

(x)=B

sin



lπx



,l=1, 2, 3,....

In a similar manner, we let ν = −β

to obtain

Y (y)=C cos βy + D sin βy

and accordingly,

(y)=D

sin



mπy



,m=1, 2, 3,....

We again choose γ

= λ + µ + ν = λ − α

− β

so that

Z (z)=E cos (γz)+F sin (γz) .

Applying the homogeneous conditions in z, we obtain

(z)=F

sin



nπz



Since the solution of equation (10.8.7) is

T (t)=G cos



√

λct



+ H sin



√

λct



the solution of the wave equation has the form

u (x , y, z, t)=

∞



l=1

∞



m=1

∞



n=1



lmn

cos

√

λct+ b

lmn

sin

√

λct



×sin



lπx



sin



mπy



sin



nπz



where a

lmn

and b

lmn

are arbitrary constants. The coeﬃcients a

lmn

are

determined from the initial condition u (x, y, z, 0) = f (x, y, z) and are found

to be

lmn

abd



f (x, y, z)sin



lπx



sin



mπy



sin



nπz



dx dy dz.

Similarly the coeﬃcients b

lmn

are d etermined from the initial condition

u (x , y, z, 0) = g (x, y, z) and are found to be

lmn

√

λacbd



g (x, y, z)sin



lπx



sin



mπy



sin



nπz



dx dy dz,

where

λ =



