Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

9.6 Neumann Problem for a Circle 341

+ b

log r



2π

f (τ) dτ,

+ b

−n



2π

f (τ)cosnτ dτ,

+ d

−n



2π

f (τ)sinnτ dτ,

and

+ b

log r



2π

g (τ) dτ,

+ b

−n



2π

g (τ)cosnτ dτ,

+ d

−n



2π

g (τ)sinnτ dτ.

The constants a

, b

, a

, b

, c

, d

for n =1, 2, 3,... can then be deter-

mined. Hence, the solution of the Dirichlet problem for an annulus is gi ven

by (9.5.3).

9.6 Neumann Problem for a Circle

Let u be a solution of the Neumann problem

∇

u =0 inD,

∂u

∂n

= f on B.

It is evident that u + constant is also a solution. Thus, we see that the

solution of the Neumann problem is not unique, and it diﬀers from another

by a constant.

Consider the interior Neumann problem

∇

u =0,r<R, (9.6.1)

∂u

∂n

∂u

∂r

= f (θ) ,r= R. (9.6.2)

Before we determine a solution of the Neumann problem, a necessary

condition for the existence of a solution will be established.

In Green’s second formula





v∇

u − u∇



dS =





∂u

∂n

− u

∂v

∂n



ds, (9.6.3)

we put v =1,sothat∇

v =0inD and ∂v/∂n =0onB. Then, the result

342 9 Boundary-Value Problems and Applications



∇

udS =



∂u

∂n

ds. (9.6.4)

Substituting of (9.6.1) and (9.6.2) into equation (9.6.4) yields



fds= 0 (9.6.5)

whichmayalsobewrittenintheform



2π

f (θ) dθ =0. (9.6.6)

As in the case of the interior Dirichlet problem for a circle, the solution

of the Laplace equation is

u (r, θ)=

∞



k=1

cos kθ + b

sin kθ) . (9.6.7)

Diﬀerentiating this with respect to r and applying the boundary condition

(9.6.2), we obtain

∂u

∂r

(R, θ)=

∞



k=1

k−1

cos kθ + b

sin kθ)=f (θ ) . (9.6.8)

Hence, the coeﬃcients are given by

kπR

k−1



2π

f (τ)coskτ dτ, k =1, 2, 3,...,

(9.6.9)

kπR

k−1



2π

f (τ)sinkτ dτ, k =1, 2, 3,....

Note that the expansion of f (θ) in a series of the form (9.6.8) is possible

only by virtue of the compatibility condition (9.6.6) since



2π

f (τ) dτ =0.

Inserting a

and b

in equation (9.6.7), we obtain

u (r, θ)=



2π



∞



k=1





cos k (θ − τ)



f (τ) dτ.

Using the identity

−

log

1+ρ

− 2ρ cos (θ − τ )

∞



k=1

cos {k (θ − τ)},

9.7 Dirichlet Problem for a Rectangle 343

with ρ =(r/R), we ﬁnd that

u (r, θ)=

−

2π



2π

log

− 2rR cos (θ − τ )+r

f (τ) dτ. (9.6.10)

in which a constant factor R

in the argument of the logarithm was elimi-

nated by virtue of equation (9.6.6).

In a similar manner, for the exterior Neumann problem, we can readily

ﬁnd the solution in the form

u (r, θ)=

2π



2π

log

− 2rR cos (θ − τ )+r

f (τ) dτ. (9.6.11)

9.7 Dirichlet Problem for a Rectangle

We ﬁrst consider the bound ary-value problem

∇

u = u

+ u

=0, 0 <x<a, 0 <y<b, (9.7.1)

u (x , 0) = f (x) ,u(x, b)=0, 0 ≤ x ≤ a, (9.7.2)

u (0,y)=0,u(a, y)=0, 0 ≤ y ≤ b. (9.7.3)

We seek a nontrivial separable solution in the f orm

u (x , y)=X (x) Y (y)

Substituting u (x, y) in the Laplace equation, we obtain

′′

− λX =0, (9.7. 4)

′′

+ λY =0, (9.7.5)

where λ is a separation constant. Since the boundary conditions are homo-

geneous for x = 0 and x = a, we choose λ = −α

with α>0inorderto

obtain nontrivial solutions of the eigenvalue problem

′′

+ α

X =0,

X (0) = X (a)=0.

It is easily found that the eigenvalues are

α =

nπ

,n=1, 2, 3,....

and the corresponding eigenfunctions are sin (nπx/a). Hence

(x)=B

sin



nπx



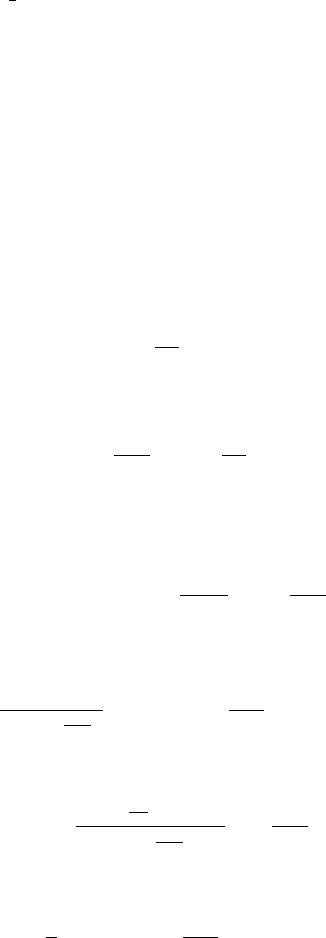
344 9 Boundary-Value Problems and Applications

The solution of equation (9.7.5) is Y (y)=C cosh αy + D sinh αy,which

mayalsobewrittenintheform

Y (y)=E sinh α (y + F ) ,

where E =



− C



and F =(1/α) tanh

−1

(C/D). Applying the re-

maining homogeneous boundary condition

u (x , b)=X (x) Y (b)=0,

we obtain

Y (b)=E sinh α (b + F )=0,

and hence,

F = −b, E =0

for a nontrivial solution u (x, y). Thus, we have

(y)=E

sinh

(

nπ

(y − b)

)

Because of linearity, the solution becomes

u (x , y)=

∞



n=1

sin



nπx



sinh

(

nπ

(y − b)

)

where a

= B

. Now, we apply the nonhomogeneous b oun dary condition

to obtain

u (x , 0) = f (x)=

∞



n=1

sinh



−nπb



sin



nπx



This is a Fourier sine series and hence,

−2

a sinh



nπb





f (x)sin



nπx



dx.

Thus, the formal solution is given by

u (x , y)=

∞



n=1

∗

sinh

nπ

(b − y)

sinh



nπb



sin



nπx



, (9.7.6)

where

∗



f (x)sin



nπx



dx.

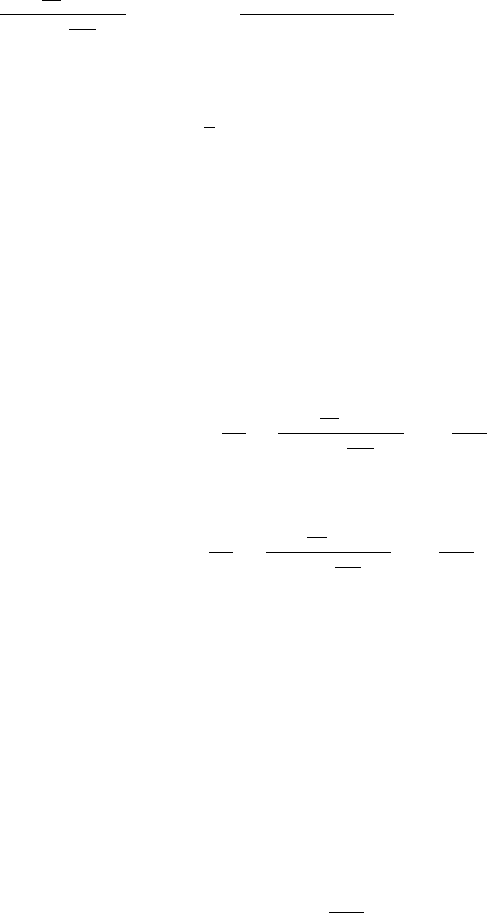
9.7 Dirichlet Problem for a Rectangle 345

To prove the existence of solution (9.7.6), we ﬁrst note that

sinh

nπ

(b − y)

sinh

nπb

= e

−nπ y/a



1 − e

−(2nπ/a)(b−y)

1 − e

−2nπ b/a



≤ C

−nπ y/a

where C

is a constant. Since f (x) is bounded, we have

∗

|≤



|f (x)|dx = C

Thus, the series for u (x, y) is dominated by the series

∞



n=1

−nπy

for y ≥ y

> 0,M= constant,

and hence, u (x, y) converges uniformly in x and y whenever 0 ≤ x ≤ a,

y ≥ y

> 0. Consequently, u (x, y) is continuous in this region and satisﬁes

the boundary values u (0,y)=u (a, y)=u (x, b)=0.

Now diﬀerentiating u twice with respect to x, we obtain

(x, y)=

∞



n=1

−a

∗



nπ



sinh

nπ

(b − y)

sinh

nπb

sin



nπx



and diﬀerentiating u twice with respect to y, we obtain

(x, y)=

∞



n=1

∗



nπ



sinh

nπ

(b − y)

sinh

nπb

sin



nπx



It is evident that the series for u

and u

are both dominated by

∞



n=1

∗

−nπy

and hence, converge uniformly for any 0 <y

<b. It follows that u

and

exist, and hence, u satisﬁes the Laplace equation.

It now remains to show that u (x, 0) = f (x). Let f (x) be a continuous

function and let f

′

(x) be piecewise continuous on [0,a]. If, in addition,

f (0) = f (a) = 0, then, the Fourier series for f (x) converges uniformly.

Putting y = 0 in the series f or u (x, y), we obtain

u (x , 0) =

∞



n=1

∗

sin



nπx



Since u (x, 0) converges uniformly to f (x), we write, for ε>0,

(x, 0) − s

(x, 0)| <ε for m, n > N

346 9 Boundary-Value Problems and Applications

where

(x, y)=

∞



n=1

∗

sin



nπx



We also know that s

(x, y) − s

(x, y) satisﬁes the Laplace equation and

the boundary conditions at x =0,x = a and y = b. Then, by the maximum

principle,

(x, y) − s

(x, y)| <ε for m, n > N

in the region 0 ≤ x ≤ a,0≤ y ≤ b. Thus, the series for u (x, y)converges

uniformly, and as a consequence, u (x, y) is continuous in the region 0 ≤

x ≤ a,0≤ y ≤ b. Hence, we obtain

u (x , 0) =

∞



n=1

∗

sin



nπx



= f (x) .

Thus, the solution (9.7.6) is established.

The general Dirichlet problem

∇

u =0, 0 <x<a, 0 <y<b,

u (x , 0) = f

(x) ,u(x, a)=f

(x) , 0 ≤ x ≤ a,

u (0,y)=f

(y) ,u(b, y)=f

(y) , 0 ≤ y ≤ b

can be solved by separating it into four problems, each of which has one

nonhomogeneous boundary condition and the rest zero. Thus, determining

each solution as in the preceding problem and then adding the four solu-

tions, the solution of the Dirichlet problem for a rectangle can be obtained.

9.8 Dirichlet Problem Involving the Poisson Equation

The solution of the Dirichlet problem involving the Poisson equation can be

obtained for simple regions when the solution of the corresponding Dirichlet

problem for the Laplace equation is known.

Consider the Poisson equation

∇

u = u

+ u

= f (x , y)inD,

with the condition

u = g (x, y)onB.

Assume that the solution can be written in the form

u = v + w,

9.8 Dirichlet Problem Involving the Poisson Equation 347

where v is a particular solution of the Poisson equation and w is the solution

of the associated homogeneous equation, th at is,

∇

w =0,

∇

v = f.

As soon as v is ascertained, the solution of the Dirichlet problem

∇

w =0 inD,

w = −v + g (x, y)onB

can be determined. The usual method of ﬁnding a parti cular solution for

the case in which f (x, y) is a polynomial of degree n is to seek a solution in

the form of a polynomial of degree (n + 2) with undetermined coeﬃcients.

As an example, we consider the torsion problem

∇

u = −2, 0 <x<a, 0 <y<b,

u (0,y)=0,u(a, y)=0; u (x, 0) = 0,u(x, b)=0.

We let u = v + w. Now assume v to b e the form

v (x, y)=A + Bx + Cy + Dx

+ Exy + Fy

Substituting this in the Poisson equation, we obtain

2D +2F = −2.

The simplest way of satisfying this equation is to choose

D = −1andF =0.

The remaining coeﬃcients are arbitrary. Thus, we take

v (x, y)=ax − x

so that v reduces to zero on the sides x = 0 and x = a. Next, we ﬁnd w

from

∇

w =0, 0 <x<a, 0 <y<b,

w (0,y)=−v (0,y)=0,

w (a, y)=−v (a, 0) = 0,

w (x, 0) = −v (x, 0) = −



ax − x



w (x, b)=−v (x, b)=−



ax − x



As in the Dirichlet problem (Section 9.7), the solution is found to be

w (x, y)=

∞



n=1



cosh

nπy

+ b

sinh

nπy



sin



nπx



348 9 Boundary-Value Problems and Applications

Application of the nonhomogeneous boundary conditions yields

w (x, 0) = −



ax − x



∞



n=1

sin



nπx



w (x, b)=−



ax − x



∞



n=1



cosh

nπb

+ b

sinh

nπb



sin



nπx



from which we ﬁnd





− ax



sin



nπx





0, if n is even

−8a

if n is odd

and



cosh

nπb

+ b

sinh

nπb







− ax



sin



nπx



dx.

Thus, we have



1 − cosh

nπb



sinh



nπb



Hence, the solution of the Dirichlet problem for the Poisson equation is

given by

u (x , y)=(a − x) x

−

∞



n=1

sinh (2n − 1)

π (b−y)

+sinh(2n − 1)

πy

sinh (2n − 1)

πb

sin (2n − 1)

πx

(2n − 1)

9.9 The Neumann Problem for a Rectangle

Consider the Neumann problem

∇

u =0, 0 <x<a, 0 <y<b, (9.9.1)

(0,y)=f

(y) ,u

(a, y)=f

(y) , 0 ≤ y ≤ b, (9.9.2)

(x, 0) = g

(x) ,u

(x, b)=g

(x) , 0 ≤ x ≤ a. (9.9.3)

The compatibility condition that must be fulﬁlled in this case is



(x) − g

(x)] dx +



(y) − f

(y)] dy =0. (9.9.4)

We assume a solution in the form

9.9 The Neumann Problem for a Rectangle 349

u (x , y)=u

(x, y)+u

(x, y) , (9.9.5)

where u

(x, y) is a solution of

∇

=0,

∂u

∂x

(0,y)=0,

∂u

∂x

(a, y)=0, (9.9.6)

∂u

∂x

(x, 0) = g

(x) ,

∂u

∂x

(x, b)=g

(x) ,

and where g

and g

satisfy the compatibility condition



(x) − g

(x)] dx =0. (9.9.7)

The function u

(x, y) is a solution of

∇

=0,

∂u

∂x

(0,y)=f

(y)

∂u

∂x

(a, y)=f

(y) (9.9.8)

∂u

∂y

(x, 0) = 0,

∂u

∂y

(x, b)=0,

where f

and f

satisfy the compatibility condition



(y) − f

(y)] dy =0. (9.9.9)

Hence, u

(x, y)andu

(x, y) can b e determined. Conditions (9.9.7) and

(9.9.9) ensure that condition (9.9.4) is fu lﬁll ed. Thus, the problem is solved.

However, the solution obtained in this manner is rather restrictive. In

general, condition (9.9.4) does not imply conditions (9.9.7) and (9.9.9).

Thus, generally speaking, it is not p ossible to obtain a solution of the

Neumann problem for a rectangle by the method described above.

To obtain a general solution, Grunberg (1946) proposed the following

method. Suppose we assume a solution in the form

u (x , y)=

(y)+

∞



n=1

(x) Y

(y) , (9.9.10)

350 9 Boundary-Value Problems and Applications

where X

(x)=cos(nπx/a) is an eigenfunction of the eigenvalue problem

′′

+ λX =0,

′

(0) = X

′

(a)=0,

corresponding to the eigenvalue λ

=(nπ/a)

. Then, from equation

(9.9.10), we see that

(y)=



u (x , y) X

(x) dx,



u (x , y)cos



nπx



dx. (9.9.11)

Multiplying both sides of equation (9.9.1) by 2 cos (nπx/a) and integrating

with respect to x from 0 to a, we obtain



+ u

)cos



nπx



dx =0,

or,

′′



cos



nπx



dx =0.

Integrating the second term by parts and appl ying the boundary conditions

(9.9.2), we obtain

′′

(y) −



nπ



(y)=F

(y) , (9.9.12)

where F

(y)=2[f

(y) − (−1)

(y)] /a. This is an ordi nary diﬀerential

equation whose solution may be written in th e form

(y)=A

cosh



nπy



+ B

sinh



nπy



πn



(τ)sinh

(

nπ

(y − τ )

)

dτ. (9.9.13)

The coeﬃcients A

and B

are determined from the boundary conditions

′

(0) =



(x, 0) cos



nπx





(x)cos



nπx



dx (9.9.14)

and

′

(b)=



(x)cos



nπx



dx. (9.9.15)