Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

12.18 Exercises 531

52. Prove that th e Fourier sine and cosine transforms are linear.

53. If F

(n) is the Fourier sine transform of f (x)on0≤ x ≤ l, show that

′′

(x)] =

2nπ

[f (0) − (−1)

f (l)] −



nπ



(n) .

54. If F

(n) is the Fourier cosine transform of f (x)on0≤ x ≤ l ,show

that

′′

(x)] =

[(−1)

′

(l) − f

′

(0)] −



nπ



(n) .

When l = π, show that

′′

(x)] =

[(−1)

′

(π) − f

′

(0)] − n

(n) .

55. By the transform method, solve

= u

+ g (x, t) , 0 <x<π, t>0,

u (x , 0) = f (x) , 0 ≤ x ≤ π,

u (0,t)=0,u(π, t) → 0 t>0.

56. By the transform method, solve

= u

+ g (x, t) , 0 <x<π, t>0,

u (x , 0) = 0, 0 <x<π,

u (0,t)=0,u

(π, t)+hu (π, t)=0,t>0.

57. By the transform method, solve

= u

+ g (x, t) , 0 <x<π, t>0,

u (x , 0) = 0, 0 <x<π,

u (0,t)=0,u

(π, t)=0,t>0.

58. By the transform method, solve

= u

− hu, 0 <x<π, t>0,

u (x , 0) = sin x, 0 ≤ x ≤ π,

u (0,t)=0,u(π, t)=0,t>0.

59. By the transform method, solve

= u

+ h, 0 <x<π, t>0,h= constant,

u (x , 0) = 0,u

(x, 0) = 0, 0 <x<π,

(0,t)=0,u

(π, t)=0,t>0.

532 12 Integral Transform Methods with Applications

60. By the transform method, solve

= u

+ g (x) , 0 <x<π, t>0,

u (x , 0) = 0,u

(x, 0) = 0, 0 <x<π,

u (0,t)=0,u(π, t)=0,t>0.

61. By the transform method, solve

+ c

xxxx

=0, 0 <x<π, t>0,

u (x , 0) = 0,u

(x, 0) = 0, 0 <x<π,

u (0,t)=0,u(π, t)=0,t>0.

(0,t)=0,u

(π, t)=sint, t ≥ 0.

62. Find the temperature distribution u (r, t) in a long cylinder of radius

a when the initial temperature is constant, u

, and radiation occurs at

the surface into a medium with zero temperature. Here u (r, t) satisﬁes

the initial boundary-problem

= κ





, 0 ≤ r<a, t>0,

+ αu =0 at r = a, t > 0,

u (r, 0) = u

for 0 ≤ r<a,

where κ and α are constants.

63. Apply the ﬁ nite Fourier sine transform to solve the longitudinal dis-

placement ﬁeld in a uniform bar of length l and cross section A sub-

jected to an external force FA ap plied at the end x = l. The governing

equation and boundary and initial conditions are

= u





, 0 <x<l, t>0,

u (0,t)=0 Eu(l, t)=F, t > 0,

u (x , 0) = u

(x, 0) = 0, 0 <x<l,

where E is the constant Young’s modulus, ρ is th e density, and F is

constant.

64. Use the ﬁnite Fourier cosine transform to solve the heat conduction

problem

= κu

, 0 <x<l, t>0,

(x, t)=0 at x = 0 and x = l, t > 0,

u (x , 0) = u

for 0 <x<l,

where u

and κ are constant.

12.18 Exercises 533

65. Use the Mellin transform to ﬁnd the solution of the integral equation



∞

−∞

f (x) k (xt) dx = g (t) ,t>0.

66. Use the Mellin transform to show the following results:

(a)

∞



n=1

f (n)=

2πi



c+i∞

c−i∞

ζ (p) F (p) dp,

(b)

∞



n=1

f (nx)=M

−1

[ζ (p) F (p)],

where ζ (s) is the Riemann zeta function deﬁned by (6.7.13).

67. Show that the solution of the boundary-value problem

+ u

=0,r≥ 0,z>0,

u (r, 0) = u

for 0 ≤ r ≤ a,

u (r, z) → 0asz →∞,

u (r, z)=au



∞

(ak) J

(kr) e

−kz

dk.

68. Show that the asymptotic representation of the Bessel f un ction J

(kr)

for large kr is

(kr)=



cos (nθ − kr sin θ) dθ ∼



πkr



cos



kr −

nπ

−



69. (a) Use the Laplace transform to solve the heat condu ction problem

= κu

, 0 <x<∞,t>0,

u (x , 0) = 0,x>0,

u (0,t)=f (t) ,u(x, t) → 0asx →∞,t>0.

(b) Derive Duhamel’s formula

u (x , t)=



f (t − τ )



∂u

∂τ



dτ,

where



∂u

∂t



√

4πκ

−3/2

exp



−

4κt



Nonlinear Partial Diﬀerential Equations with

Applications

“True Laws of Nature cannot be linear.”

Albert Einstein

“... the progress of physics will to a large extent depend on the p rogr ess

of nonlin ear mathematics, of methods to solve nonlinear equations ... and

therefore we can learn by comparing diﬀerent nonlinear problems.”

Werner Heisenberg

13.1 Introduction

The three-dimensional linear wave equation

= c

∇

u, (13.1.1)

arises in the areas of elasticity, ﬂuid dynamics, acoustics, magnetohydrody-

namics, and electromagnetism.

The general solution of the one-dimensional equation (13.1.1) is

u (x , t)=φ (x − ct)+ψ (x + ct) , (13.1.2)

where φ and ψ are determined by the initial or boundary conditions. Phys-

ically, φ and ψ represent waves moving with constant speed c and without

change of shape, along the positive and the n egative directions of x respec-

tively.

The solutions φ and ψ correspond to the two factors when the one-

dimensional equation (13.1.1) is written in the form



∂

∂t

+ c

∂

∂x



∂

∂t

− c

∂

∂x



u =0. ( 13.1.3)

536 13 Nonlinear Partial Diﬀerential Equations with Applications

Obviously, the simplest linear wave equation is

+ cu

=0, (13.1.4)

and its solution u = φ (x − ct) represents a wave moving with a constant

velocity c in the positive x-direction without change of shape.

13.2 One-Dimensional Wave Equation and Method of

Characteristics

The simplest ﬁ rst-order nonlinear wave equation is given by

+ c (u) u

=0, −∞ <x<∞,t>0, (13.2.1)

where c (u) is a given function of u.

We solve this nonlinear equation subject to the initial condition

u (x , 0) = f (x) , −∞ <x<∞. (13.2.2)

Before we discuss the method of solution, the following comments are

in order. First, unlike linear diﬀerential equations, the principle of super-

position cannot be applied to ﬁnd the general solution of nonlinear partial

diﬀerential equations. Second, the eﬀect of nonlinearity can change the en-

tire nature of the solution. Third, a study of the above initial-value problem

reveals most of the important ideas for nonlinear hyperbolic waves. Finally,

a large number of physical and engineering probl ems are governed by the

above nonlinear system or an extension of it.

Although the nonlinear system governed by (13.2.1)–(13.2.2) looks sim-

ple, it poses nontrivial problems in applied mathematics, and it l eads sur -

prisingly to new phenomena. We solve the system by the method of char-

acteristics.

In order to construct continuous solutions, we consider the total diﬀer-

ential du given by

du =

∂u

∂t

dt +

∂u

∂x

dx, (13.2.3)

so that the points (x, t) are assumed to lie on a curve Γ . Then, dx/dt

represents the slope of the curve Γ at any point P on Γ . Thus, equation

(13.2.3) becomes

= u





. (13.2.4)

It follows from this result that (13.2.1) can be regarded as the ordinary

diﬀerential equation

=0, (13.2.5)

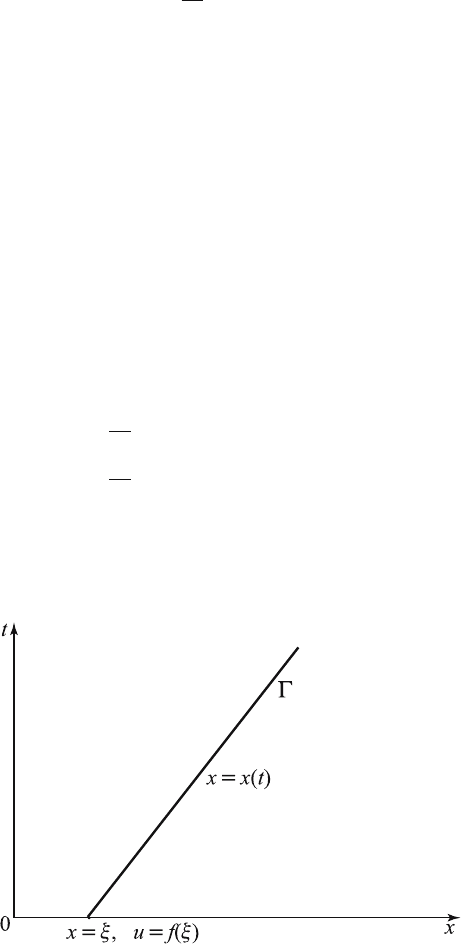
13.2 One-Dimensional Wave Equation and Method of Characteristics 537

along any member of the family of curves Γ which are the solution curves

= c (u) . (13.2.6)

These curves Γ are called the characteristic curves of the main equation

(13.2.1). Thus, the solution of (13.2.1) has been reduced to the solution of

a pair of simultaneous ordinary diﬀerential equations (13.2.5) and (13.2.6).

Clearly, both the characteristic speed and the characteristics depend on the

solution u.

Equation (13.2.5) implies that u = constant along each characteristic

curve Γ ,andeachc (u) remains constant on Γ . Therefore, (13.2.6) shows

that the characteristic curves of (13.2.1) form a family of straight lines in

the (x, t)-plane with slope c (u). This in dicates that the general solution of

(13.2.1) depends on ﬁnding the family of lines. Also, each line with slope

c (u) corresponds to the value of u on it. If the initial point on the charac-

teristic curve Γ is denoted by ξ and if one of the curves Γ intersects t =0

at x = ξ,thenu (ξ, 0) = f (ξ) on the whole of that curve Γ as shown in

Figure 13.2.1.

Thus, we have the following characteristic form on Γ :

= c (u) ,x(0) = ξ, (13.2.7)

=0,u(ξ, 0) = f (ξ) . (13.2.8)

These constitute a pair of coupled ordinary diﬀerential equations on Γ.

Equation (13.2.7) cannot be solved independently because c is a function

of u. However, (13.2.8) can readily be solved to obtain u = constant and

Figure 13.2.1 A characteristic curve.

538 13 Nonlinear Partial Diﬀerential Equations with Applications

hence, u = f (ξ) on the whole of Γ . Thus, (13.2.7) leads to

= F (ξ) ,x(0) = ξ, (13.2.9)

where

F (ξ)=c (f (ξ)) . (13.2.10)

Integrating equation (13.2.9) gives

x = tF (ξ)+ξ. (13.2.11)

This represents the characteristic curve which is a straight line whose slope

is not a constant, but depends on ξ .

Combining these results, we obtain the solution of the initial-value prob-

lem in parametric form

u (x , t)

f (ξ)

ξ + tF (ξ)



, (13.2.12)

where

F (ξ)=c (f (ξ)) .

We next verify that this ﬁnal form represents an analytic expression of

the solution. Diﬀerentiati ng (13.2.12) with respect to x and t, we obtain

= f

′

(ξ) ξ

= f

′

(ξ) ξ

1={1+tF

′

(ξ)}ξ

0=F (ξ)+{1+tF

′

(ξ)}ξ

Elimination of ξ

and ξ

gives

′

(ξ)

1+tF

′

(ξ)

= −

F (ξ) f

′

(ξ)

1+tF

′

(ξ)

. (13.2.13)

Since F (ξ)=c (f (ξ)), equation (13.2.1) is satisﬁed provided 1+tF

′

(ξ) =0.

The solution (13.2.12) also satisﬁes the initial condition at t =0,since

ξ = x, and the solution (13.2.12) is unique.

Suppose that u (x, t)andv (x, t) are two solutions. Then, on x = ξ +

tF (ξ),

u (x , t)=u (ξ, 0) = f (ξ)=v (x, t) .

Thus, we have proved the following:

13.2 One-Dimensional Wave Equation and Method of Characteristics 539

Theorem 13.2.1. The nonlinear initial-value problem

+ c (u) u

=0, −∞ <x<∞,t>0,

u (x , t)=f (x) , at t =0, −∞ <x<∞,

has a unique solution provided 1+tF

′

(ξ) =0, f and c are C

(R) functions

where F (ξ)=c (f (ξ)).

The solution is given in the parametric form:

u (x , t)=f (ξ) ,

x = ξ + tF (ξ) .

Remark: When c (u)=constant=c>0, equation (13.2.1) becomes the

linear wave equation (13.1.4). The characteristic curves are x = ct + ξ and

the solution u is given by

u (x , t)=f (ξ)=f (x − ct) .

Physical Signiﬁcance of (13.2.12).

We assume c (u) > 0. The graph of u at t = 0 is the graph of f. In view of

the fact

u (x , t)=u (ξ + tF (ξ) ,t)=f (ξ

)

the point (ξ,f (ξ)) moves parallel to the x-axis in the positive direction

through a distance tF (ξ)=ct, and the distance moved (x = ξ + ct)de-

pends on ξ. This is a typical nonlinear phenomenon. In the linear case, the

curve moves parallel to the x-axis with constant velocity c, and the solu-

tion r epresents waves travelling without change of shape. Thus, there is a

striking diﬀerence between the linear and the nonlinear solution.

Theorem 13.2.1 asserts that the solution of the nonlinear initial-value

problem exists provided

1+tF

′

(ξ) =0,x= ξ + tF

′

(ξ) . (13.2.14)

However, the former condition is always satisﬁed for suﬃciently small time

t. By a solution of the problem, we mean a diﬀerentiable function u (x, t).

It follows from results (13.2.13) that both u

and u

tend to inﬁnity as

1+tF

′

(ξ) → 0. This means that the solution develops a singularity (dis-

continuity) when 1 + tF

′

(ξ) = 0. We consider a point (x, t)=(ξ,0) so that

this condition is satisﬁed on the characteristics through the point (ξ,0) at

atimet such that

t = −

′

(ξ)

(13.2.15)

540 13 Nonlinear Partial Diﬀerential Equations with Applications

which is positive provided F

′

(ξ)=c

′

(f) f

′

(ξ) < 0. If we assume c

′

(f) > 0,

the above inequality implies that f

′

(ξ) < 0. Hence, the solution (13.2.12)

ceases t o exist for all time if the initial data is such that f

′

(ξ) < 0forsome

value of ξ. Suppose t = τ is the time when the solution ﬁrst develops a

singularity (discontinuity) for some value of ξ.Then

τ = −

min

−∞<ξ<∞

′

(f) f

′

(ξ)}

> 0.

We draw the graphs of the nonlinear solution u (x, t)=f (ξ)belowfor

diﬀerent values of t =0,τ,2τ, .... The shape of the initial curve for u (x, t)

changes with increasing values of t, and the solution becomes multiple-

valued for t ≥ τ . Therefore, the solution breaks down when F

′

(ξ) < 0for

some ξ, and such breaking is a typical nonlinear phenomenon. In linear

theory, such breaking will never occur.

More precisely, the development of a singularity in the solution for t ≥ τ

can be seen by the following consideration. If f

′

(ξ) < 0, we can ﬁnd two

values of ξ = ξ

, ξ

(ξ

<ξ

) on the initial line such that the characteristics

through them have diﬀerent slopes 1/c (u

)and1/c (u

)whereu

= f (ξ

)

and u

= f (ξ

)andc (u

) <c(u

). Thus, these two characteristics will

intersect at a point in the (x, t)-plane for some t>0. Since the character-

istics carry constant values of u, the solution ceases to be single-valued at

their point of intersection. Figure 13.2.2 shows that th e wave proﬁle pro-

gressively distorts itself, and at any instant of time there exists an interval

on the x-axis, where u assumes three values for a given x. The end result

is the development of a nonunique solution, and this leads to breaking.

Therefore, when conditions (13.2.14) are violated the solu tion develops

a discontinuity known as a shock. The analysis of shock involves extension

of a solution to allow for discontinuities. Also, it is necessary to impose on

the solution certain restrictions to b e satisﬁed across its discontinuity. This

point will be discussed further in a subsequent section.

13.3 Linear Dispersive Waves

We consider a single linear partial diﬀerential equation with constant coef-

ﬁcients in the form



∂

∂t

∂

∂x

∂

∂y

∂

∂z



u (x,t)=0, (13.3.1)

where P is a polynomial in partial derivatives and x =(x, y, z).

We seek an elementary plane wave solution of (13.3.1) in the form

u (x,t)=ae

i(κ

κ·x−ωt)

, (13.3.2)

where a is the amplitude, κ

κ =(k, l, m) is the wavenumber vector, ω is

the frequency and a, κ

κ, ω are constants. When this plane wave solution is