Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

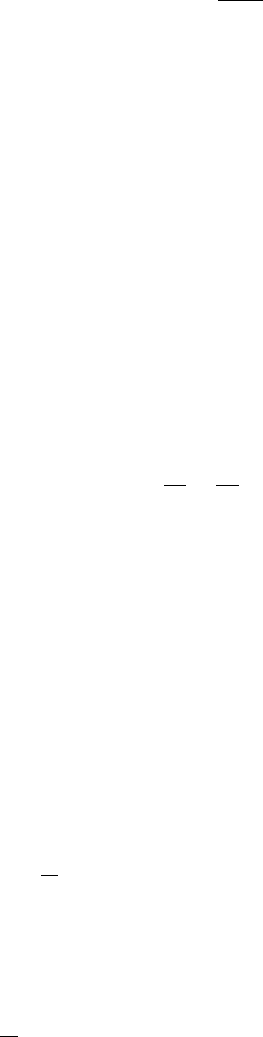
13.9 Discontinuous Solutions and Shock Waves 561

x = X (τ )+



γ +1

X (τ )



(t − τ) . (13.8.46)

It is noted that the family Γ

represents straight lines with slope dx/dt

increasing with velocity u. Consequently, the characteristics ar e likely to

overlap on the piston, that is,

X (τ ) > 0 for any τ.Ifu increases, so do c,

ρ,andp so that instability develops. It shows that sho cks will be formed in

the compressive part of the disturbance.

13.9 Discontinuous Solutions and Shock Waves

The development of a nonunique solution of a nonlinear hyperbolic equation

has already been discussed in connection with several diﬀerent problems. In

real physical situations, this nonuniqueness usually manifests itself in the

formation of discontinuous solutions which propagate in the medium. Such

discontinuous solutions across some surf ace are called shock waves. These

waves are found to occur widely in high speed ﬂows in gas dynamics.

In order to investigate the nature of discontinuous solutions, we recon-

sider the nonlinear conservation equation (13.6.5) that is,

∂ρ

∂t

∂q

∂x

=0. (13.9.1)

This equation has b een solved under two basic assumptions: (i) There exists

a functional relation between q and ρ,thatis,q = Q (ρ); (ii) ρ and q

are continuously diﬀerentiable. In some physical situations, the solution of

(13.9.1) leads to breaking phenomenon. When breaking occurs, questions

arise about the validity of these assumptions. To examine the formation

of discontinuities, we consider the following: (a) we assume the relation

q = Q (ρ) but allow jump discontinuity for ρ and q; (b) in addition to the

fact that ρ and q are continuously diﬀerentiable, we assume that q is a

function of ρ and ρ

. One of the simplest forms is

q = Q (ρ) − νρ

,ν>0. (13.9. 2)

In case (a), we assume the conservation equation (13.6.1) still holds and

has the form



ρ (x, t) dx + q (x

,t) − q (x

,t)=0. (13.9.3)

We now assume that there is a discontinuity at x = s (t)wheres is a

continuously diﬀerentiable function of t,andx

and x

are chosen so that

>s(t) >x

,andU (t)= ˙s (t). Equation (13.9.3) can be written as





−

ρdx+



ρdx



+ q (x

,t) − q (x

,t)=0,

562 13 Nonlinear Partial Diﬀerential Equations with Applications

which implies that



−

dx +˙sρ



−





dx − ˙sρ





+ q (x

,t) − q (x

,t)=0,

(13.9.4)

where ρ (s

−

,t), ρ (s

,t) are the values of ρ (x, t)asx → s from below and

above respectively. Since ρ

is bounded in each of the intervals separately,

the integrals tend to zero as x

→ s

−

and x

→ s

. Thus, in the limit,





− q



−



= U





− ρ



−

'

. (13.9.5)

In the conventional notation of shock dynamics, this can be written as

− q

= U (ρ

− ρ

) , (13.9.6)

−U [ρ]+[q]=0, (13.9.7)

where subscripts 1 and 2 are used to denote the values behind and ahead

of the shock respectively, and [ ] denotes the discontinuous jump in the

quantity involved. Equation (13.9.7) is called the shock condition. Thus, the

basic problem can be written as

∂ρ

∂t

∂q

∂x

= 0 at points of continuity, (13.9.8)

−U [ρ]+[q] = 0 at points of discontinuity. (13.9.9)

Therefore, we have a nice correspondence

∂ρ

∂t

↔−U [],

∂

∂x

↔ [], (13.9.10)

between the diﬀerential equation and the shock condition.

It i s now possible to ﬁnd discontinuous solutions of (13.9.3). In any

continuous part of the solution, equation (13.9.1) is still satisﬁed and the

assumption q = Q (ρ) remains valid. But we have q

= Q (ρ

)andq

Q (ρ

) on the two sides of any shock, and the shock condition (13.9.6) has

the form

U (ρ

− ρ

)=Q (ρ

) − Q (ρ

) . (13.9.11)

Example 13.9.1. The simplest example in which breaking occurs is

+ c (ρ) ρ

=0,

with discontinuous initial data at t =0

13.10 Structure of Shock Waves and Burgers’ Equation 563

ρ =

⎧

⎨

⎩

,x<0

,x>0

, (13.9.12)

and

F (x)=

⎧

⎨

⎩

= c

(ρ) ,x<0

= c

(ρ) ,x>0

, (13.9.13)

where

>ρ

and c

In this case, breaking will occur immediately and this can be seen from

Figure 13.9.1ab with c

′

(ρ) > 0. The multivalu ed region b egins at the origin

ξ = 0 and is bounded by the characteristics x = c

t and x = c

t with

. This corresponds to a centered compression wave with overlapping

characteristics in the ( x , t)-plane.

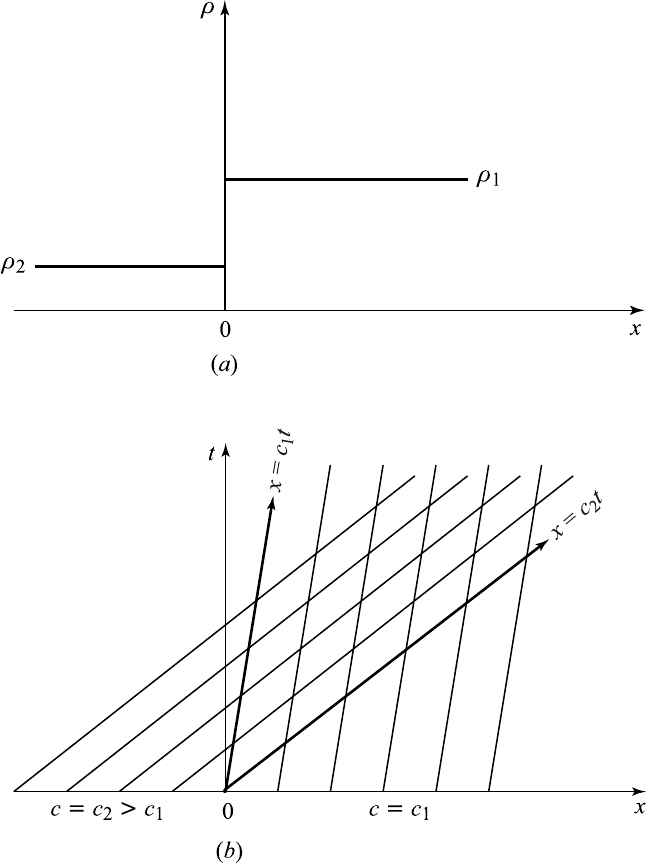
On the other hand, if the initial condition is expansive with c

there is a continuous solution obtained from (13.2.12) in which all values

of F (x)in[c

] are taken on characteristics through the origin ξ =0.

This corresponds to a centered fan of characteristics x = ct, c

≤ c ≤ c

in the (x, t)-plane so that the solu tion has the explicit form c =(x/t),

< (x/t) <c

. The density distribution and the expansion wave are

shown in Figure 13.9.2ab.

In this case, the complete solution is given by

c =

⎧

⎪

⎨

⎪

⎩

,x≤ c

t<x<c

,x≥ c

(13.9.14)

13.10 Structure of Shock Waves and Burgers’ Equation

In order to resolve b reakin g, we assumed a functional relation in ρ and q

with appropriate shock conditions. Now we investigate the case when

q = Q (ρ) − νρ

,ν>0. (13.10.1)

Note that near breaking where ρ

is large, (13.10.1) gives a better approx-

imation. With (13.10.1), the basic equation (13.9.1) becomes

+ c (ρ) ρ

= νρ

, (13.10.2)

564 13 Nonlinear Partial Diﬀerential Equations with Applications

Figure 13.9.1ab Density distribution and centered compression wave with over-

lapping characteristics.

13.10 Structure of Shock Waves and Burgers’ Equation 565

Figure 13.9.2ab Density distribution and centered expansion wave.

566 13 Nonlinear Partial Diﬀerential Equations with Applications

where c (ρ)=Q

′

(ρ), the second and the third terms represent the eﬀects

on nonlinearity and diﬀusion.

We ﬁrst solve (13.10.2) for two simple cases: (i) c (ρ)=constant=c,

and (ii) c (ρ) ≡ 0. In the ﬁrst case, equation (13.10.1) becomes linear and

we seek a plane wave solution

ρ (x, t)=a exp {i (kx − ωt)}. (13.10.3)

Substituting this solution into the lin ear equation (13.10.2), we have the

dispersion relation

ω = ck − iνk

, (13.10.4)

where

Im ω = −νk

< 0, since ν>0.

Thus, the wave proﬁle has the form

ρ (x, t)=ae

−νk

exp [ik (x − ct)] (13.10.5)

which represents a diﬀusive wave (Im ω<0) with wavenumbers k and phase

velocity c whose amplitude decays exponentially with time t. The decay

time is given by t



νk



−1

which becomes smaller and smaller as k

increases with ﬁxed ν. Thus, the waves of smaller wavelengths decay faster

than waves of longer wavelengths. On the other hand, for a ﬁxed wavenum-

ber k, t

decreases as ν increases so that waves of a given wavelength atten-

uate faster in a medium with larger ν. The quantity ν may be regarded as

a measure of diﬀusion . Final ly, after a suﬃciently long time (t ≫ t

)only

disturbances of long wavelength will survive, while all short wavelength

disturbances will decay rapidly.

In the second case, (13.10.2) reduces to the linear diﬀusion equation

= νρ

. (13.10.6)

This equation with the initial data at t =0

ρ =

⎧

⎨

⎩

,x<0

,x>0,

>ρ

, (13.10.7)

can readily be solved, and the solution for t>0is

ρ (x, t)=

√

πν t



−∞

−(x−ξ)

/4νt

dξ +

√

πν t



∞

−(x−ξ)

/4νt

dξ.

(13.10.8)

After some manipulation involving changes of variables of integration

(x − ξ) /2

√

νt = η, the solution is simpliﬁed to the form

13.10 Structure of Shock Waves and Burgers’ Equation 567

u (x , t)=

(ρ

+ ρ

)+(ρ

− ρ

)

√



x/2

√

νt

−η

dη, (13.10.9)

(ρ

+ ρ

(ρ

− ρ

)erf



√

νt



. (13.10.10)

This shows that the eﬀect of the term νρ

is to smooth out the initial

distribution (νt)

−

. The solution tends to values ρ

, ρ

as x →

+ ∞.The

absence of the term νρ

in (13.10.2) leads to nonlinear steepening and

breaking. Indeed, equation (13.10.2) combines the two opposite eﬀects of

breaking and diﬀusion. The sign of ν is important; indeed, solutions are

stable or unstable according as ν>0orν<0.

In order to investigate solutions that balance between steepening and

diﬀusion, we seek solutions of (13.10.2) in the form

ρ = ρ (X) ,X= x − Ut, (13.10.11)

where U is a constant to be determined.

It follows from (13.10.2) that

[c (ρ) − U] ρ

= νρ

. (13.10.12)

Integrating this equation gives

Q (ρ) − Uρ + A = νρ

, (13.10.13)

where A is a constant of integration.

Integrating (13.10.13) with resp ect to X gives an implicit relation for

ρ (X) in the form



dρ

Q (ρ) − Uρ + A

. (13.10.14)

We would like to have a solution which tends to ρ

, ρ

as X →

+ ∞.If

such a solution exists with ρ

→ 0as|X|→∞, the quantities U and A

must satisfy

Q (ρ

) − Uρ

+ A = Q (ρ

) − Uρ

+ A =0, (13.10.15)

which implies that

U =

Q (ρ

) − Q (ρ

)

− ρ

. (13.10.16)

This is exactly the same as the shock velocity obtain ed before.

Result (13.10.15) shows that ρ

, ρ

are zeros of Q (ρ) − Uρ + A.In

the limit ρ → ρ

or ρ

, the integral (13.10.14) diverges an d X → +

∞.If

′

(ρ) > 0, then Q (ρ)−Uρ+A ≤ 0inρ

≤ ρ ≤ ρ

and then ρ

≤ 0 because

568 13 Nonlinear Partial Diﬀerential Equations with Applications

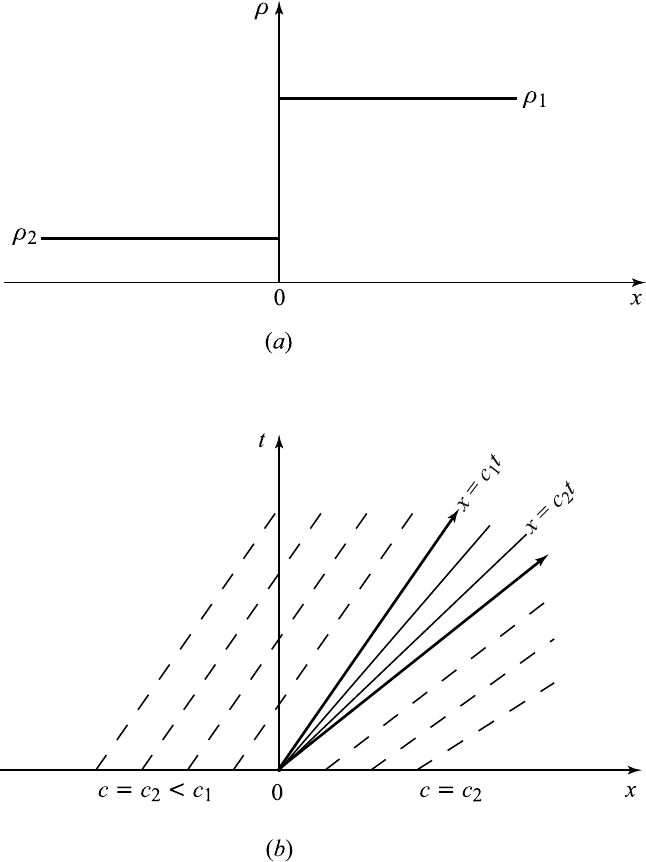
Figure 13.10.1 Shock structure and shock thickness.

of (13.10.11). Thus, ρ decreases monotonically from ρ

at X = −∞ to ρ

at X = ∞ as shown in Figure 13.10.1.

Physically, a continuous waveform carrying an increase in ρ will progres-

sively distort itself and eventually break forward and require a shock with

<ρ

provided c

′

(ρ) > 0. It will break backward and require a shock

with ρ

>ρ

and c

′

(ρ) < 0.

Example 13.10.1. Obtain the solution of (13.10.2) with the initial data

(13.10.7) and Q (ρ)=αρ

+ βρ + γ, α>0.

We write

Q (ρ) − Uρ + A = −α (ρ

− ρ)(ρ − ρ

) ,

where

U = β + α (ρ

+ ρ

)andA = αρ

− γ.

Integral (13.10.14) becomes

= −



dρ

(ρ − ρ

)(ρ

− ρ)

α (ρ

− ρ

)

log



− ρ

ρ − ρ



which gives the solution

ρ (X)=ρ

+(ρ

− ρ

)

exp

αX

(ρ

− ρ

)

1+exp

αX

(ρ

− ρ

)

. (13.10.17)

13.10 Structure of Shock Waves and Burgers’ Equation 569

The exponential factor in the solution indicates the existence of a tran-

sition layer of thickness δ of the order of ν/[α (ρ

− ρ

)]. This can also be

referred to as the shock thickness. The thickness δ increases as ρ

→ ρ

for

aﬁxedν. It tends to zero as ν → 0foraﬁxedρ

and ρ

In this case, the shock velocity (13.10.16) becomes

U = α (ρ

− ρ

)+β =

+ c

) , (13.10.18)

where c (ρ)=Q

′

(ρ), c

= c (ρ

), and c

= c (ρ

We multiply (13.10.2) by c

′

(ρ) and simplify to obtain

+ cc

= νc

− νc

′′

(ρ) ρ

. (13.10.19)

Since Q (ρ) is a quadratic expression in ρ,thenc (ρ)=Q

′

(ρ) becomes

linear in ρ and c

′′

(ρ) = 0. Thus, (13.10.19) leads to Burgers’ equation

replacing c with u

+ uu

= νu

. (13.10.20)

This equation incorporates the combined opposite eﬀects of nonlinearity

and diﬀusion . It is the simplest nonlinear model equation for diﬀusive waves

in ﬂuid dynamics. Using the Cole–Hopf transformation

u = −2ν

. (13.10.21)

Burgers’ equation can be solved exactly, and th e opposite eﬀects of nonlin-

earity and diﬀusion can be investigated in some detail.

We introduce the transformation in two steps. First, we write u = ψ

so that (13.10.20) can readily be integrated to obtai n

= νψ

. (13.10.22)

Thenextstepistointroduceψ = −2ν log φ and to transform this

equation into the so called diﬀusion equation

= νφ

. (13.10.23)

This equation was solved in earlier chapters. We simply quote the solu-

tion of the initial-value problem of (13.10.23) with the initial data

φ (x, 0) = Φ (x) , −∞ <x<∞. (13.10.24)

The solution for φ is

φ (x, t)=

√

πν t



∞

−∞

Φ (ζ)exp



−

(x − ζ)

4νt



dζ, (13.10.25)

570 13 Nonlinear Partial Diﬀerential Equations with Applications

where Φ (ζ) can be written in terms of the initial value u (x, 0) = F (x)by

using (13.10.21). It turns out that, at t =0,

φ (x, t)=Φ (x)=exp



−

2ν



F (α) dα



. (13.10.26)

It is then convenient to write down φ (x, t) in the form

φ (x, t)=

√

πν t



∞

−∞

exp



−

2ν



dζ, (13.10.27)

where

f (ζ,x, t)=



F (α) dα +

(x − ζ)

. (13.10.28)

Consequently,

(x, t)=−

4ν

√

πν t



∞

−∞

(x − ζ)

exp



−

2ν



dζ. (13.10.29)

Therefore, the solution for u follows from (13.10.21) and has the form

u (x , t)=

∞

−∞



x−ζ



exp



−

2ν



dζ

∞

−∞

exp



−

2ν



dζ

. (13.10.30)

Although this is the exact solution of Burgers’ equation, p hysical inter-

pretation can hardly be given unless a suitably simple form of F (x) is sp ec-

iﬁed. Even then, ﬁnding an exact evaluation of the integrals in (13.10.30)

is a formidable task. It is then necessary to resort to asymptotic methods.

Before we deal with asymptotic analysis, the following example may be

considered for an investigation of shock formation.

Example 13.10.2. Find the solution of Burgers’ equation with physical sig-

niﬁcance for the case

F (x)=

⎧

⎨

⎩

Aδ(x) ,x<0

0,x>0.

We ﬁrst ﬁnd

f (ζ,x, t)=A



δ (α) dα +

(x − ζ)

⎧

⎪

⎨

⎪

⎩

(x−ζ)

− A, ζ < 0

(x−ζ)

,ζ>0.