Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.


12.18 Exercises 521
When α = 1, solution (12.17.87) becomes
ψ (x, t)=
∞
−∞
G (x − ξ, t) ψ
0
(ξ) dξ, (12.17.89)
where the Green’s function G (x, t)isgivenby
G (x, t)=
1
2π
∞
−∞
e
ikx
E
1,1
−ak
2
t
dk
=
1
2π
∞
−∞
exp
ikx − atk
2
dk
=
1
√
4πat
exp
−
x
2
4at
. (12.17.90)
This solution (12.17.89) is in perfect agreement with the classical solution
obtained by Debnath (1995).
12.18 Exercises
1. Find the Fourier tr ansform of
(a) f (x)=exp
−ax
2
,(b)f (x)=exp(−a |x|),
where a is a constant.
2. Find the Fourier transform of the gate function
f
a
(x)=
⎧
⎨
⎩
1, |x| <a, ais a positive constant .
0, |x|≥a.
3. Find the Fourier tr ansform of
(a) f (x)=
1
|x|
,(b)f (x)=χ
[−a,a]
(x)=
⎧
⎨
⎩
1, −a<x<a
0, otherwise,
(c) f (x)=
⎧
⎨
⎩
1 −
|x|
a
, |x|≤a
0, |x|≥a,
(d) f (x)=
1
(x
2
+a
2
)
.
4. Find the Fourier tr ansform of
(a) f (x)=sin
x
2
,(b)f (x)=cos
x
2
.

522 12 Integral Transform Methods with Applications
5. Show that
I =
∞
0
e
−a
2
x
2
dx =
√
π/2a, a > 0,
by noting that
I
2
=
∞
0
∞
0
e
−a
2
(
x
2
+y
2
)
dx dy =
π/2
0
∞
0
e
−a
2
r
2
rdrdθ.
6. Show that
∞
0
e
−a
2
x
2
cos bx dx =
√
π/2a
e
−b
2
/4a
2
,a>0.
7. Prove that
(a) f (x)=
1
√
2π
∞
−∞
e
ikx
F (k) dk = F
−1
{F (k)},
(b) F [f (ax − b)] =
1
|a|
e
ikb/a
F (k/a) .
8. Prove the following properties of the Fourier convolution :
(a) f (x) ∗ g (x)=g (x) ∗ f (x), (b) f ∗ (g ∗ h)=(f ∗ g) ∗ h,
(c) f ∗(ag + bh)=a (f ∗ g)+b (f ∗h), where a and b are constants,
(d) f ∗ 0=0∗ f =0, (e)f ∗1 = f,
(f) f ∗
√
2πδ= f =
√
2πδ∗ f,
(g) F{f (x) g (x)} =(F ∗ G)(k)=
1
√
2π
∞
−∞
F (k − ξ) G (ξ) dξ,
9. Prove the following properties of the Fourier convolution :
(a)
d
dx
{f (x) ∗ g (x)} = f
′
(x) ∗ g (x)=f (x) ∗ g
′
(x),
(b)
d
2
dx
2
[(f ∗g)(x)]=(f
′
∗ g
′
)(x)=(f
′′
∗ g)(x),
(c) (f ∗ g)
(m+n)
(x)=
f
(m)
∗ g
(n)
!
(x),
(d)
∞
−∞
(f ∗g)(x) dx =
∞
−∞
f (u) du
∞
−∞
g (v) dv.
(e) If g (x)=
1
2a
H (a − x), then
(f ∗g)(x)istheaveragevalueoff (x)in[x − a, x + a].
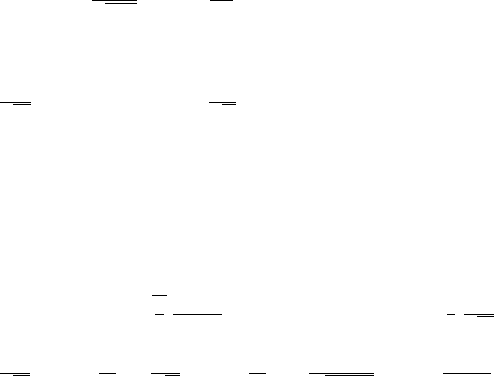
12.18 Exercises 523
(f) If G
t
(x)=
1
√
4πkt
exp
−
x
2
4κt
,then(G
t
∗ G
s
)(x)=G
t+s
(x).
10. Prove the following results:
(a)
1
√
2π
∞
−∞
e
−k
2
t−ikx
dk =
1
√
2t
e
−x
2
/4t
,
(b)
∞
−∞
F (k) g (k) e
ikx
dk =
∞
−∞
f (y) G (y − x) dy,
(c)
∞
−∞
F (k) g (k) dk =
∞
−∞
f (y) G (y) dy,
(d) sin x ∗ e
−a|x|
=
%
2
π
a sin x
(1+a
2
)
,(e)e
ax
∗ χ
[0,∞)
(x)=
1
a
e
ax
√
2π
,a>0,
(f)
1
√
2a
exp
−
x
2
4a
∗
1
√
2b
exp
−
x
2
4b
=
1
√
2(a+b)
exp
−
x
2
4(a+b)
.
11. Determine the solution of th e initial-value problem
u
tt
= c
2
u
xx
, −∞ <x<∞,t>0,
u (x , 0) = f (x) ,u
t
(x, 0) = g (x) , −∞ <x<∞.
12. Solve
u
t
= u
xx
,x>0,t>0,
u (x , 0) = f (x) ,u(0,t)=0.
13. Solve
u
tt
= c
2
u
xxxx
=0, −∞ <x<∞,t>0,
u (x , 0) = f (x) ,u
t
(x, 0) = 0, −∞ <x<∞.
14. Solve
u
tt
+ c
2
u
xxxx
=0,x>0,t>0,
u (x , 0) = 0,u
t
(x, 0) = 0,x>0,
u (0,t)=g (t) ,u
xx
(0,t)=0,t>0.
15. Solve
φ
xx
+ φ
yy
=0, −a<x<a, 0 <y<∞,
φ
y
(x, 0) =
⎧
⎨
⎩
δ
0
, 0 < |x| <a,
0, |x| >a.
φ (x, y) → 0 uniformly in x as y →∞.
524 12 Integral Transform Methods with Applications
16. Solve
u
t
= u
xx
+ tu, −∞ <x<∞,t>0,
u (x , 0) = f (x) ,u(x, t) is bounded, −∞ <x<∞.
17. Solve
u
t
− u
xx
+ hu = δ (x) δ (t) , −∞ <x<∞,t>0,
u (x , 0) = 0,u(x, t) → 0 uniformly in t as |x|→∞.
18. Solve
u
t
− u
xx
+ h (t) u
x
= δ (x) δ (t) , 0 <x<∞,t>0,
u (x , 0) = 0,u
x
(0,t)=0,
u (x , t) → 0 uniformly in t as x →∞.
19. Solve
u
xx
+ u
yy
=0, 0 <x<∞, 0 <y<∞,
u (x , 0) = f (x) , 0 ≤ x<∞,
u
x
(0,y)=g (y) , 0 ≤ y<∞,
u (x , y) → 0 uniformly in x as x →∞and uniformly in y as x →∞.
20. Solve
u
xx
+ u
yy
=0, −∞ <x<∞, 0 <y<a,
u (x , 0) = f (x) ,u(x, a)=0, −∞ <x<∞,
u (x , y) → 0 uniformly in y as |x|→∞.
21. Solve
u
t
= u
xx
,x>0,t>0,
u (x , 0) = 0,x>0,u(0,t)=f (t) ,t>0,
u (x , t) is bounded for all x and t.
22. Solve
u
xx
+ u
yy
=0,x>0, 0 <y<1,
u (x , 0) = f (x) ,u(x, 1) = 0,x>0,
u (0,y)=0,u(x, y) → 0 uniformly in y as x →∞.
12.18 Exercises 525
23. Find the Laplace transform of each of the following functions:
(a) t
n
,(b)cosωt, (c) sinh kt,
(d) cosh kt,(e)te
at
,(f)e
at
sin ωt,
(g) e
at
cos ωt,(h)t sinh kt,(i)t cosh kt,
(j)
%
1
t
,(k)
√
t,(l)
sin at
t
.
24. Find the inverse transform of each of the following functions:
(a)
s
(s
2
+a
2
)(s
2
+b
2
)
,(b)
1
(s
2
+a
2
)(s
2
+b
2
)
,
(c)
1
(s−a)(s−b)
,(d)
1
s(s+a)
2
,
(e)
1
s(s+a)
,(f)
s
2
−a
2
(s
2
+a
2
)
2
.
25. The velocity potential φ (x, z, t) and the free-surface evaluation η (x, t)
for surface waves in water of infinite depth satisfy the Laplace equation
φ
xx
+ φ
zz
=0, −∞ <x<∞, −∞ <z≤ 0,t>0,
with the free-surface, boundary, and in itial conditions
φ
z
= η
t
on z =0,t>0,
φ
t
+ gη =0 on z =0,t>0,
φ
z
→ 0asz →−∞,
φ (x, 0, 0) = 0 and η (x, 0) = f (x) , −∞ <x<∞,
where g is the constant acceleration due to gravity.
Show that
φ (x, z, t)=−
√
g
√
2π
∞
−∞
k
−
1
2
F (k) e
|k|z−ikx
sin
g |k|t
dk,
η (x, t)=
1
√
2π
∞
−∞
F (k) e
−ikx
cos
g |k|t
dk,
where k represents the Fourier transform variable.
Find the asymptotic solution for η (x, t)ast →∞.
26. Use the Fourier transform method to show that the solution of the
one-dimensional Schr¨odinger equation for a free particle of mass m,
iψ
t
= −
2
2m
ψ
xx
, −∞ <x<∞,t>0,
ψ (x, 0) = f (x) , −∞ <x<∞,

526 12 Integral Transform Methods with Applications
where ψ and ψ
x
tend to zero as |x|→∞,andh =2π is the Planck
constant, is given by
ψ (x, t)=
1
√
2π
∞
−∞
f (ξ) G (x − ξ) dξ,
where G (x, t)=
(1−i)
2
√
γt
exp
"
−
x
2
4iγt
#
is the Green’s function and γ =
2m
.
27. Prove the following properties of the Laplace convolution:
(a) f ∗ g = g ∗ f ,(b)f ∗ (g ∗ h)=(f ∗ g) ∗ h,
(c) f ∗ (αg + βh)=α (f ∗g)+β (f ∗ h), α and β are constants,
(d) f ∗0=0∗ f,
(e)
d
dt
[(f ∗g)(t)] = f
′
(t) ∗ g (t)+f (0) g (t),
(f)
d
2
dt
2
[(f ∗g)(t)] = f
′′
(t) ∗ g (t)+f
′
(0) g (t)+f (0) g
′
(t),
(g)
d
n
dt
n
[(f ∗g)(t)] = f
(n)
(t) ∗ g (t)+
n−1
k=0
f
(k)
(0) g
(n−k−1)
(t).
28. Obtain the solution of the problem
u
tt
= c
2
u
xx
, 0 <x<∞,t>0,
u (x , 0) = f (x) ,u
t
(x, 0) = 0,
u (0,t)=0,u(x, t) → 0 uniformly in t as x →∞.
29. Solve
u
tt
= c
2
u
xx
, 0 <x<l, t>0,
u (x , 0) = 0,u
t
(x, 0) = 0,
u (0,t)=f (t) ,u(l, t)=0,t≥ 0.
30. Solve
u
t
= κu
xx
, 0 <x<∞,t>0,
u (x , 0) = f
0
, 0 <x<∞,
u (0,t)=f
1
,u(x, t) → f
0
uniformly in t as x →∞,t>0.
31. Solve
u
t
= κu
xx
, 0 <x<∞,t>0,
u (x , 0) = x , x > 0,
u (0,t)=0,u(x, t) → x uniformly in t as x →∞,t>0.

12.18 Exercises 527
32. Solve
u
t
= κu
xx
, 0 <x<∞,t>0,
u (x , 0) = 0, 0 <x<∞,
u (0,t)=t
2
,u(x, t) → 0 uniformly in t as x →∞,t≥ 0.
33. Solve
u
t
= κu
xx
− hu, 0 <x<∞,t>0,h= constant,
u (x , 0) = f
0
,x>0,
u (0,t)=0,u
x
(0,t) → 0 uniformly in t as x →∞,t>0.
34. Solve
u
t
= κu
xx
, 0 <x<∞,t>0,
u (x , 0) = 0, 0 <x<∞,
u (0,t)=f
0
,u(x, t) → 0 uniformly in t as x →∞,t>0.
35. Solve
u
tt
= c
2
u
xx
, 0 <x<∞,t>0,
u (x , 0) = 0,u
t
(x, 0) = f
0
, 0 <x<∞,
u (0,t)=0,u
x
(x, t) → 0 uniformly in t as x →∞,t>0.
36. Solve
u
tt
= c
2
u
xx
, 0 <x<∞,t>0,
u (x , 0) = f (x) ,u
t
(x, 0) = 0, 0 <x<∞,
u (0,t)=0,u
x
(x, t) → 0 uniformly in t as x →∞,t>0.
37. A semi-infinite lossless transmission line has no initial current or poten-
tial. A time dependent EMF , V
0
(t) H (t)isappliedattheendx =0.
Find the potential V (x, t). Then determine the potential for cases: (i)
V
0
(t)=V
0
= constant, and (ii) V
0
(t)=V
0
cos ωt.
38. Solve the Blasius problem of an unsteady boundary layer flow in a semi-
infinite body of viscous fluid enclosed by an infinite horizontal disk at
z = 0. The governing equation, boundary, and initial conditions are
∂u
∂t
= ν
∂
2
u
∂z
2
,z>0,t>0,
u (z, t)=Ut on z =0,t>0,
u (z, t) → 0asz →∞,t>0,
u (z, t)=0 at t ≤ 0,z>0.
Explain the implication of the solution.
528 12 Integral Transform Methods with Applications
39. The stress-strain relation and equation of motion for a viscoelastic rod
in the absence of external force are
∂e
∂t
=
1
E
∂σ
∂t
+
σ
η
,
∂σ
∂x
= ρ
∂
2
u
∂t
2
,
where e is the strain, η is the coefficient of viscosity, and the displace-
ment u (x, t) is related to the strain by e = ∂u/∂x. Prove that the stress
σ (x, t) satisfies the modified wave equation
∂
2
σ
∂x
2
−
ρ
η
∂σ
∂t
=
1
c
2
∂
2
σ
∂t
2
,c
2
= E/ρ.
Show that the stress distribution in a semi-infinite viscoelastic rod sub-
ject to the boundary and initial conditions,
˙u (0,t)=UH(t) ,σ(x, t) → 0asx →∞,t>0,
σ (x, 0) = 0, ˙u (x, 0) = 0,
is given by
σ (x, t)=−Uρcexp
−
Et
2η
I
0
Et
2η
t
2
−
x
2
c
2
1
2
H
t −
x
c
.
40. An elastic string is stretched between x = 0 and x = l and is initially
at rest in the equilibrium position. Show that the Laplace transform
solution for the displacement field subject to the boundary conditions
y (0,t)=f (t)andy (l, t)=0,t>0is
y (x, s)=f (s)
sinh
&
s
c
(l − x)
'
sinh
sl
c
.
41. The end x = 0 of a semi-infinite submarine cable is maintained at
a potential V
0
H (t). If the cable has no initial current and potential,
determine the potential V (x, t)atpointx and at time t.
42. Obtain the solution of the Stokes–Ekman problem (see Debnath, 1995)
of an unsteady boundary layer flow in a semi-infinite body of viscous
fluid bounded by an infinite horizontal disk at z = 0, when both the
fluid and the disk rotate with a uniform angular velocity Ω about the z-
axis. The governing boundary layer equation, the boundary condi tions,
and the initial conditions are
∂q
∂t
+2Ωiq = ν
∂
2
q
∂z
2
,z>0,t>0,
q (z,t)=ae
iω t
+ be
−iω t
on z =0,t>0,
q (z,t) → 0asz →∞,t>0,
q (z,t)=0 at t ≤ 0, for all z>0,

12.18 Exercises 529
where q = u + iv,isthecomplexvelocityfield,ω is the frequency
of oscillations of the disk, and a and b are complex constants. Hence,
deduce the steady-state solution, and determine the structure of the
associated boundary layers.
43. Show that, when ω = 0 in the Stokes–Ekman problem 42, the steady
flow field is given by
q (z,t) ∼ (a + b)exp
/
−
2iΩ
ν
1
2
z
0
.
Hence determine the thickness of the Ekman layer.
44. For problem 14 (e) (iii) in 3.9 Exercises, show that the potential V (x, t)
and the current I (x, t) satisfy the partial differential equation
∂
2
∂t
2
+2k
∂
∂t
+ k
2
(V,I)=c
2
∂
2
∂x
2
(V,I) .
Find the solution for V (x, t) with the boundary and initial data
V (x, t)=V
0
(t)atx =0,t>0,
V (x, t) → 0asx →∞,t>0,
V (x, 0) = V
t
(x, 0) = 0 for 0 ≤ x<∞.
45. Use the Laplace transform to solve the Abel integral equation
g (t)=
t
0
f
′
(τ)(t − τ)
−α
dτ, 0 <α<1.
46. Solve Abel’s problem of tautochronous motion described in problem 17
of 14.11 Exercises.
47. The velocity potential φ (r, z, t) and the free-surface elevation η (r, t)
for axisymmetric surface waves in water of infinite depth satisfy the
equation
φ
rr
+
1
r
φ
r
+ φ
zz
=0, 0 ≤ r<∞, −∞ <z≤ 0,t>0,
with the free-surface, boundary, and in itial conditions
φ
z
= η
z
on z =0,t>0,
φ
t
+ gη =0, on z =0,t>0,
φ
z
→ 0,z→−∞,
φ (r, 0, 0) = 0, and η (r, 0) = f (r) , 0 ≤ r<∞,
where g is the acceleration due to gravity and f (r) represents the initial
elevation.
Show that

530 12 Integral Transform Methods with Applications
φ (r, z, t)=−
√
g
∞
0
√
k
5
f (k) J
0
(kr) e
kz
sin
gk t
dk,
η (r, t)=
∞
0
k
5
f (k) J
0
(kr)cos
gk t
dk,
where
5
f (k) is the zero-order Hankel transform of f (r).
Derive the asymptotic solution
η (r, t) ∼
gt
2
2
3
2
r
3
5
f
gt
2
4r
2
cos
gt
2
4r
as t →∞.
48. Write the solution for the Cauchy–Poisson problem where the initial
elevation is concentrated in the neighborhood of the origin , that is,
f (r)=(a/2πr) δ (r), where a is the total volume of the fl uid displaced.
49. The steady temp erature distribution u (r, z) in a semi-infinite solid with
z ≥ 0 is governed by the system
u
rr
+
1
r
u
r
+ u
zz
= −Aq (r) , 0 <r<∞,z>0,
u (r, 0) = 0,
where A is a constant and q (r ) represents the steady heat source. Show
that the solution is given by
u (r, z)=A
∞
0
5q (k) J
0
(kr) k
−1
1 − e
−kz
dk,
where 5q (k) is the zero-order Hankel t ransfor m of q (r).
50. Find the solution for the small deflection u (r)ofanelasticmembrane
subjected to a concentrated loading distrib ution which i s governed by
u
rr
+
1
r
u
r
− κ
2
u =
1
2π
δ (r)
r
, 0 ≤ r<∞,
where u and its derivatives vanish as r →∞.
51. Obtain the solution for the potential v (r, z) due to a flat electrified disk
of radius unity with the center of the disk at the origin and the axis
along the z-axis. The function v (r, z) satisfies th e Laplace equation
v
rr
+
1
r
v
r
− v
zz
=0, 0 <r<∞,z>0,
with the boundary conditions
v (r, 0) = v
0
, 0 ≤ r<1,
v
z
(r, 0) = 0,r>1.
