Mrinal K Pal. Power system stability
Подождите немного. Документ загружается.

TURBINE-GENERATOR SHAFT TORSIONALS
9-19
on the location of the speed sensor on the shaft system, the signal may contain an appreciable
amount of one or more shaft system natural frequency components. These signals acting through
the excitation system can produce air-gap torques at the shaft natural frequencies, thereby
reinforcing the shaft system oscillations. This can be minimized or eliminated, either by
positioning the speed sensor close to a suitable node point (the point at which the shaft motion
contains zero or minimum amount of a particular frequency component as indicated by the
particular mode shape), or by generating the signal indirectly from quantities, such as,
accelerating power, that are relatively free of these frequencies.
Development of Detailed Electrical System Model
An exact analysis in which the impact of electrical transients, self-excitation and torsional
interaction are included simultaneously, can be undertaken by combining the shaft system model
with that for the electrical system. However, a more detailed model for the electrical system than
is required for conventional stability studies would be needed. A lumped parameter model can
still be used. However, the terms that give rise to electrical transients at normal system (power)
frequency and electrical natural frequencies must be included. A single-machine model in which
a generator is connected to a large system (infinite bus) through a transmission line is usually
sufficient, unless the generator being studied is closely coupled electrically with other generators.
This is because the high frequency transients are usually short lived, and tend to be localized
unlike the low frequency transients involving rotor swings. (The high frequency transients do not
generally affect the rotor swing mode appreciably -- hence the justification of neglecting these in
stability studies.)
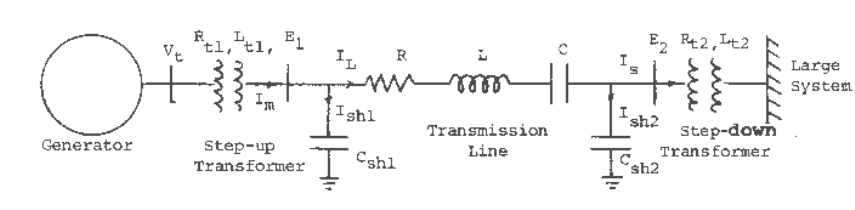
The system to be considered is shown in Figure 9.6.
Fig. 9.6 A generator connected to a large system through a series compensated transmission line.
The transmission line is represented by an equivalent lumped parameter model. For generality, a
step-down transformer has been added at the far end.
A detailed synchronous machine model has been presented in Chapter 5. The relevant equations,
assuming one damper winding on each axis, are listed below.
Flux linkage equations:
qqqaqq
ddfddfdadd
ddffdffddadfd
qaqqqq
dadfdadddd
ixix
ixixix
ixixix
ixix
ixixix
1111
11111
11
1
1
+−=
++−=
++−=
+−=
+
+
−=
ψ
ψ
ψ
ψ
ψ
(9.35)
TURBINE-GENERATOR SHAFT TORSIONALS
9-20
Voltage equations:
qq
q
dd
d
fdfd
fd
fd
qd
q
q
dq
d
d
ir
dt
d
ir
dt
d
ir
dt
d
e
ir
dt
d
e
ir
dt
d
e
11
1
o
11
1
o
o
oo
oo
1
0
1
0
1
1
1
+=
+=
+=
−+=
−−=
ψ
ω
ψ
ω
ψ
ω
ψ
ω
ω
ψ
ω
ψ
ω
ω
ψ
ω
(9.36)
Air-gap torque:
dqqde
iiT
ψ
ψ
−
= (9.37)
Equations for the transmission system:
The various voltage and current quantities and the circuit parameters are shown on Figure 9.6
using subscripts associating them with the various sections. The equations, in phase quantities,
for the section between the machine terminal and the high-voltage bus of the step-up transformer
can be written as
c
c
tctc
b
b
tbtb
a
a
tata
E
dt
di
LiRe
E
dt
di
LiRe
E
dt
di
LiRe
111
111
111
++=
++=
++=
(9.38)
where
e
a
, e
b
, e
c
are the instantaneous phase voltages at the generator terminal etc. The equations
can be written in matrix form as
abcabctabctabc
dt
d
LR
,111
Eiie ++= (9.39)
where
=
c
b
a
abc
e
e
e
e
etc.
Similarly,
abcshabcsh
dt
d
C
,1,1
EI = (9.40)
abcabcCabcLabcLabc
dt
d
LR
,2,,,,1
EvIIE +++= (9.41)
abcCabcL
dt
d
C
,,
vI = (9.42)

TURBINE-GENERATOR SHAFT TORSIONALS
9-21
abcshabcsh
dt
d
C
,2,2
EI = (9.43)
abcbabcStabcStabc
dt
d
LR
,,2,2,2
VIIE ++=
(9.44)
Also
abcLabcshabc ,,1
IIi
+
= (9.45)
abcSabcshabcL ,,2,
III
+
= (9.46)
Using the same transformation as used in transforming the synchronous machine phase quantities
into
d-q-o quantities, the system phase quantities can also be transformed into d-q-o quantities.
The transformation is given by, in the case of currents for example (see Chapter 5),
abcdq
iTi =
o
(9.47)
where
+−−−−
+−
=
2/12/12/1
)120sin()120sin(sin
)120cos()120cos(cos
3
2
oo
oo
θθθ
θθθ
T
The inverse transformation is
o
1
dqabc
iTi
−
= (9.48)
where
+−+
−−−
−
=
−
1)120sin()120cos(
1)120sin()120cos(
1sincos
1
oo
oo
θθ
θθ
θθ
T
Applying these transformations to the above equations we obtain
o,1o1o1o1o dqdqtdqtdqtdq
L
dt
d
LR EiSiie +++=
ω
(9.49)
since
()
ooooo
1
dqdqdqdqdq
dt
d
dt
d
dt
d
dt
d
iSiiSiiTT
ω
θ
+=+=
−
where
−
=
000
001
010
S
Similarly,
o,1o,1o,1 dqshdqshdqsh
C
dt
d
C ESEI
ω
+= (9.50)
o,2o,o,o,o,o,1 dqdqCdqLdqLdqLdq
L
dt
d
LR EvISIIE ++++=
ω
(9.51)
o,o,o, dqCdqCdqL
C
dt
d
C vSvI
ω
+=
(9.52)
TURBINE-GENERATOR SHAFT TORSIONALS
9-22
o,2o,2o,2 dqshdqshdqsh
C
dt
d
C ESEI
ω
+= (9.53)
o,o,2o,2o,2o,2 dqbdqStdqStdqStdq
L
dt
d
LR VISIIE +++=
ω
(9.54)
Also
o,o,1o dqLdqshdq
IIi
+
= (9.55)
o,o,2o, dqSdqshdqL
IIi
+
= (9.56)
When converted into per-unit form the above equations reduce to
o,1o1
o
o1
o
o1o
1
dqdqtdqtdqtdq
X
dt
d
XR EiSiie +++=
ω
ω
ω
(9.57)
o,1
o
o,1
o
o,1
22
1
dqdqdqsh
Y
dt
dY
ESEI
ω
ω
ω
+= (9.58)
o,2o,o,
o
o,
o
o,o,1
1
dqdqCdqLdqLdqLdq
X
dt
d
XR EvISIIE ++++=
ω
ω
ω
(9.59)
o,
o
o,
o
o,
111
dqC
C
dqC
C
dqL
Xdt
d
X
vSvI
ω
ω
ω
+= (9.60)
o,2
o
o,2
o
o,2
22
1
dqdqdqsh
Y
dt
dY
ESEI
ω
ω
ω
+= (9.61)
o,o,2
o
o,2
o
o,2o,2
1
dqbdqStdqStdqStdq
X
dt
d
XIR VISIE +++=
ω
ω
ω
(9.62)
where
Y is the total admittance in pu due to line charging, and X
C
is the capacitive reactance due
to the series capacitor.
Equations (9.55) and (9.56) remain unchanged.
The steady state phasor diagram is shown in Figure 9.7.
Fig. 9.7 Steady-state phasor diagram for system of Fig. 9.6.
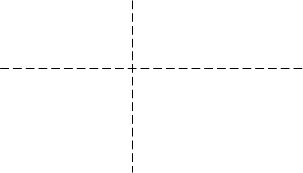
TURBINE-GENERATOR SHAFT TORSIONALS
9-23
Equations (9.55) through (9.62), along with equations (9.35) through (9.37), and equations (9.11)
through (9.15) constitute a complete description of the combined turbine-generator shaft
torsional and electrical system. For a given disturbance scenario the equations can be solved
numerically and the relative angular displacements of the rotor elements determined as functions
of time. The shaft torques are then obtained by multiplying these by the corresponding spring
constants. The effects of excitation and governor control systems can be included by adding the
appropriate equations to be above model.
Since the system response would contain a number of high frequency modes, a very small time
step would be needed in the numerical computation in order to maintain accuracy as well as
preserve the oscillations in the computed response. The procedure will therefore be extremely
time consuming if the simulation has to be continued for a fairly long period of real time which
may be necessary in order to identify the presence of self-excitation and torsional interaction.
Small Disturbance Stability Study of Turbine-Generator Shaft Torsional System
The possibility of self-excitation and/or torsional interaction can be ascertained more
conveniently through a small disturbance stability analysis, in which the system equations are
linearized about an operating point and the stability of the resulting linear system is investigated.
The analysis will first be carried out using a state-space approach, as it offers a more complete
information on the stability properties of the system. Later a simplified analysis using a
frequency response technique will be illustrated.
Since excitation and governor control systems can contribute to torsional interactions, these
should be included in the analysis. For the purpose of illustration, a typical simplified excitation
control model is included in the analysis. Inclusion of a governor model is relatively
straightforward and is therefore not considered here.
The machine flux linkage equations (9.35), after linearization, can be written in matrix form as
∆
∆
=
∆
∆
r
s
r
s
i
i
X
Ψ
Ψ
(9.63)
where
,
∆
∆
=∆
q
d
s
ψ
ψ
Ψ
∆
∆
∆
=∆
∆
∆
=∆
∆
∆
∆
=∆
q
d
fd
r
q
d
s
q
d
fd
r
i
i
i
i
i
1
1
1
1
,, iiΨ
ψ
ψ
ψ
and
−
−
−
−
−
=
qaq
ddfad
dfffdad
aqq
adadd
xx
xxx
xxx
xx
xxx
11
111
1
X
From (9.63)
ΨY
i
i
∆=
∆
∆
r
s
(9.64)
TURBINE-GENERATOR SHAFT TORSIONALS
9-24
where Y is the inverse of X and
∆
∆
=∆
r
s
Ψ
Ψ
Ψ
From (9.64), after partitioning
Y as
=
Q
P
Y
,
ΨPi
∆
=
∆
s
(9.65)
ΨQi
∆
=
∆
r
(9.66)
The machine voltage equations, after linearization, can be written in matrix form as
∆
∆
+∆+∆
−
+∆
−
=∆
q
d
s
d
q
ss
e
e
r
dt
d
oo
o
o
ωωω
ψ
ψ
ω
ω
iΨΨ
(9.67)
∆
′
+∆=∆
0
0
fd
doad
ffd
rr
E
Tx
x
dt
d
iAΨ
(9.68)
where
fd
fd
ad
fdqd
do
ffd
e
r
x
Err
T
x
=
−−
′
−= ,diag
1o1o
ωω
A
and
fd
ffd
do
r
x
T
o
ω
=
′
The air gap torque equation (9.37) can be written in matrix form as
[
]
[
]
sdqsdqe
iiT iΨ
∆
−
+
∆
−=∆
ψ
ψ
(9.69)
Using (9.65) and (9.66), equations (9.67), (9.68) and (9.69) reduce to
∆
∆
+∆+∆
−
+∆
−
=∆
q
d
d
q
ss
e
e
r
dt
d
oo
o
o
ωωω
ψ
ψ
ω
ω
ΨPΨΨ
(9.70)
∆
′
+∆=∆
0
0
fd
doad
ffd
r
E
Tx
x
dt
d
ΨQAΨ
(9.71)
[
]
[
]
ΨPΨ
∆
−
+
∆
−=∆
dqsdqe
iiT
ψ
ψ
(9.72)
The transmission system equations can be linearized and rearranged, noting that for balanced
operation the zero-sequence quantities are absent, as follows:
TURBINE-GENERATOR SHAFT TORSIONALS
9-25
From (9.57)
∆
∆
+∆
−
+∆
−
+∆=
∆
∆
q
d
d
q
t
s
tt
tt
s
t
q
d
E
E
i
i
X
RX
XR
dt
d
X
e
e
1
1
o
1
11
11
o
1
ω
ωω
ii
which can be written as, using equation (9.65) and writing
∆
∆
=∆
q
d
E
E
1
1
1
E
,
1
o
1
11
11
o
1
EΨPΨP ∆+∆
−
+∆
−
+∆=
∆
∆
ω
ωω
d
q
t
tt
tt
t
q
d
i
i
X
RX
XR
dt
d
X
e
e
(9.73)
From (9.55) and (9.58), and using (9.65)
ω
ω
ω
ωω
∆
−
+∆
−
+∆−∆=∆
d
q
L
E
E
YYdt
d
1
1
1
o
o
oo
1
22
EIΨPE
(9.74)
where
∆
∆
=∆
Lq
Ld
L
I
I
I
Similarly, from (9.56), and (9.59) through (9.62)
2
oo
o1
o
/1
1/
EvIEI ∆−∆−∆
−
+∆
−−
−
+∆=∆
XX
I
I
XR
XR
Xdt
d
C
Ld
Lq
LL
ωω
ωω
ω
(9.75)
where
∆
∆
=∆
Cq
Cd
C
v
v
v
and
∆
∆
=∆
q
d
E
E
2
2
2
E
ω
ω
ω
ω
∆
−
+∆
−
+∆=∆
Cd
Cq
CLCC
v
v
X
dt
d
vIv
o
o
o
(9.76)
ω
ω
ω
ωω
∆
−
+∆
−
+∆−∆=∆
d
q
sL
E
E
YYdt
d
2
2
2
o
o
oo
2
22
EIIE
(9.77)
where
∆
∆
=∆
sq
sd
s
I
I
I
δ
δ
δ
ω
ωω
ω
∆
−
+∆
−
+∆
−−
−
+∆=∆
sin
cos
1
1
2
o
2
2
2
2
o2
2
o
t
b
sd
sq
s
t
t
t
t
t
s
X
V
I
I
X
R
X
R
Xdt
d
IEI
(9.78)
Note that
sCL
IEvIEΨ
∆
∆∆∆∆∆ and,,,,,
21
are vectors of state variables as defined. Therefore,
equations (9.73) through (9.78) are expressed entirely in terms of state variables.

TURBINE-GENERATOR SHAFT TORSIONALS
9-26
Considering the simplified excitation control system used in Chapter 6 (Fig. 6.6, IEEE type 1),
ignoring saturation for the purpose of illustration, the linearized equations can be written in
matrix form as (see Appendix C)
t
A
A
fd
FF
AF
AF
AAF
AF
fd
V
T
K
x
E
TT
TT
KK
TTT
KK
x
E
dt
d
∆
−
+
∆
∆
−
+−
=
∆
∆
0
11
1
22
(9.79)
Since
222
qdt
eeV += , ∆V
t
can be expressed as
∆
∆
=∆
q
d
t
q
t
d
t
e
e
V
e
V
e
V
(9.80)
Therefore, (9.79) can be written as
∆
∆
+∆=∆
q
d
exexex
e
e
dt
d
LxKx
(9.81)
Substituting for
∆
∆
q
d
e
e
from (9.73), equations (9.70), (9.71), and (9.81) can be combined into
one matrix equation as shown in (9.82)
1
EGD
x
Ψ
C
x
Ψ
B
x
Ψ
∆+∆+
∆
∆
+
∆
∆
=
∆
∆
ω
exexex
dt
d
dt
d
(9.82)
where the matrices
B, C, D and G have been obtained by properly combining the constituent
matrices of equations (9.70), (9.71), (9.73), and (9.81), and augmenting with zeros as necessary.
Equation (9.82) can be reduced to
[] [] []
1
111
EGCIDCI
x
Ψ
BCI
x
Ψ
∆−+∆−+
∆
∆
−=
∆
∆
−−−
ω
exex
dt
d
(9.83)
The linearized equations of the shaft torsional system, assuming constant mechanical input, can
be written in terms of state variables as
e
T
dt
d
∆+∆=∆ JθKθ (9.84)
where
[]
′
∆∆∆∆∆∆=∆
521521
θθθθθθ
&
L
&&
Lθ
′
−=
0
2
00
4
o
H
ω
LJ
(Note that
δ
θ
=
4
, and
ωθ
=
4
&
)
and
TURBINE-GENERATOR SHAFT TORSIONALS
9-27
=
43
21
KK
KK
K
where
K
1
is a 5×5 null matrix
K
2
is a 5×5 unit matrix
−
+−
+−
+−
−
=
5
45o
5
45o
4
45o
4534
4
o
4
34o
3
34o
3423
3
o
3
23o
2
23o
2312
2
o
2
12o
1
12o
1
12o
3
22
2
)(
22
2
)(
22
2
)(
22
22
H
K
H
K
H
K
KK
HH
K
H
K
KK
HH
K
H
K
KK
HH
K
H
K
H
K
ωω
ωωω
ωωω
ωωω
ωω
K
+
−
++
−
++
−
++
−
+
−
=
5
5545o
5
45o
4
45o
4
454434o
4
34o
3
34o
3
343323o
3
23o
2
23o
2
232212o
2
12o
1
12o
1
1211o
4
2
)(
2
22
)(
2
22
)(
2
22
)(
2
22
)(
H
DD
H
D
H
D
H
DDD
H
D
H
D
H
DDD
H
D
H
D
H
DDD
H
D
H
D
H
DD
ωω
ωωω
ωωω
ωωω
ωω
K
Using equation (9.72), (9.84) reduces to
ΨMθK
θ
∆+∆=
∆
dt
d
(9.85)
Equations (9.83), (9.85) and (9.74) through (9.78) constitute the complete set of state equations
describing the system of Figure 9.6. Since these equations are expressed entirely in terms of state
variables, they can be readily combined into the form
Axx
=
&
. Small disturbance stability studies
can then be performed as detailed in Chapter 8. The necessary information on small disturbance
system performance and stability are obtained from the eigenvalues and eigenvectors of the
matrix
A. For stability, the eigenvalues of A must have negative real parts.
Estimation of Electrical Damping in Torsional Interaction
An analysis of torsional interaction using a frequency response technique will now be presented.
We will analyze the system response due to small amplitude rotor oscillations at oscillation
frequency
ω
n
corresponding to one of the torsional natural frequencies.
Assuming a small deviation
∆
ω
of rotor speed from synchronous speed
ω
o
,
tA
n
ω
ω
sin
=
∆ (9.86)
For sinusoidal oscillations at frequency
ω
n

TURBINE-GENERATOR SHAFT TORSIONALS
9-28
δωδδω
∆≡∆=∆=∆
n
js
dt
d
or
t
A
t
A
j
j
n
n
n
nn
ω
ω
ω
ω
ω
ω
δ
cossin −=−=∆
−
=∆ (9.87)
The small changes in the generator terminal voltages in terms of
d-q components, ∆e
d
and ∆e
q
,
will, in general, be linear functions of
∆
δ
and ∆
ω
. The changes in phase voltages can be obtained
from equation (9.48). For example, for phase
a
θ
θ
sincos
qda
eee
−
=
Linearizing the above expression, noting that
δ
θ
∆
=
∆
,
(
)
(
)
θ
δ
θ
δ
sincos
∆
+
∆
−
∆
−∆=∆
dqqda
eeeee (9.88)
Also, we can write
()()
t
A
jeejeeee
n
n
qd
ω
ω
δδ
cos
2121
−
+=∆+=∆−∆
and
()()
t
A
jeejeeee
n
n
dq
ω
ω
δδ
cos
4343
−
+=∆+=∆+∆
Therefore, equation (9.88) can be written as, noting that
t
o
ω
θ
=
,
() ()
ttjee
A
ttjee
A
e
n
n
n
n
a o43o21
sincoscoscos
ωω
ω
ωω
ω
+++−=∆
which reduces to, using (9.87),
[]
[
]
−−++
−
−
∆
+
−
+
∆
=∆
φ
ω
ω
φ
ω
ω
tEtEe
nna
)(cos)(cos
oo
(9.89)
where
41
32
1
41
32
1
2
32
2
41
2
32
2
41
tan,tan
)()(
2
)()(
2
ee
ee
ee
ee
eeee
A
E
eeee
A
E
n
n
−−
+−
=
+−
+
=
+−+−−=∆
+++−=∆
−
−
−
+
−
+
φφ
ω
ω
Note that considering the effects of speed change only, i.e., retaining only the speed voltage
terms in the generator voltage equations,
ω
ω
ω
ω
∆=∆∆=∆
oo
,
q
q
d
d
e
e
e
e
q
n
dd
n
q
eeeeeeee
o
43
o
21
,,,
ω
ω
ω
ω
===−=
∴
